Similar presentations:
Системы линейных алгебраических уравнений. Матрицы, действия над матрицами
1.
Практическое занятие 2. Системылинейных алгебраических
уравнений. Матрицы, действия
над матрицами
Мустафина Ляззат Мухамеджановна
Доцент кафедры Высшая математика
2.
Цель занятий по теме «Линейная алгебра»: ознакомиться с методамирешения линейных алгебраических уравнений.
Цель данного занятия: познакомиться с понятием матрицы, разобрать
виды матриц, изучить правила действия над матрицами. Рассмотреть приемы
нахождения обратной матрицы и ранга матрицы.
Для закрепления материала подготовлены ИДЗ – индивидуальные
домашние задания, которые необходимо выполнить к следующему занятию.
Задания выполняются строго по своему варианту, согласно номера в
групповом списке.
3.
Определение 1. Матрицей размерности m n называется прямоугольнаятаблица из m n чисел, расположенных в т строках и п столбцах.
Обозначаются матрицы, как правило, большими буквами A, B, C,...,
a11 a12 ... a1п
a
a
...
a
22
2п
21
A
... ... ... ...
a
a
...
a
тп
т2
т
или A aij ~ m n
Например, матрица A 2 1 2 имеет размерность 2×3: 2 строки и 3
4
столбца.
3
5
4.
1. Виды матриц1) Квадратная матрица. Матрица, имеющая одинаковое число строк и
столбцов, размерности п×п, называется квадратной матрицей порядка п.
Например, A 3
4
1 2
и
0 1 1
есть квадратные матрицы второго
B 2 0 3
1 1 1
и третьего порядков соответственно.
a11 , a22 ,...,ann
Элементы
квадратной
матрицы
А
называются
диагональными элементами (или говорят, что они лежат на главной диагонали
матрицы).
5.
2) Матрица – строка - это матрица размера1×пA (a11 ,..., a1n ) .
3) Матрица – столбец - это матрица размера m×1
b11
b21 .
B
...
bm1
6.
4) Треугольная матрица – это квадратная матрица, в которой элементы,расположенные под диагональю (или над диагональю), равны нулю.
a11
Например,
0
A
.
0
a12
a 22
.
0
... a1n
1 2
... a 2 n ,
0 3
B
0 0
... .
... a nn
0 0
3 4
0 0
2
,
0 1 C 1 1 0 .
2 3 0
1 2
0 7
5) Нулевая матрица - это матрица, все элементы которой равны нулю.
Нулевая матрица обозначается символом O .
7.
6) Единичная матрица. Квадратная матрица, все диагональные элементыкоторой равны 1, а остальные – нулю, называется единичной и обозначается
E или En , где п ее порядок. Таким образом,
1 0... 0
E 0 1... 0
0 0... 1
Определение 2. Две матрицы называются равными, если
1) матрицы имеют одинаковые размерности;
2) элементы, стоящие на соответственных местах этих матриц, равны.
8.
2. Действия над матрицами2.1. Умножение матрицы на число
Определение 3. Чтобы умножить число на матрицу A или матрицу A
на число , нужно умножить на все элементы матрицы A . Очевидно,
A A .
3 6
Пример 1. Пусть A 4 1 . Найти матрицы 2А, -3А.
2 5
9.
2.2. Сложение матрицОпределение 4. Суммой двух матриц A (aij ) ~m×n и B (bij ) ~m×n одной
размерности называется матрица
C (cij ) ~m×n той же размерности
(обозначается C A B ), элементы которой определяются равенствами:
сij aij bij , i 1,..., m; j 1,..., n .
4 3 1
0 2 3
, B
.
Пример 2. Пусть A
2 5 4
6 4 7
Найти матрицы А+В, А-В, 2А-3В.
10.
2.3. Умножение матрицВ отличие от операций сложения и умножения на число операция
умножения матрицы на матрицу определяется более сложным образом.
Определение 5. Пусть заданы две матрицы A и B, причем число столбцов
первой из них равно числу строк второй:
a11
a 21
A
.
a
m1
a12
a 22
.
am2
... a1 p
b11
... a 2 p
b21
, B
... .
.
b
... a mp
p1
b12
b22
.
b p2
... b1n
... b2 n
.
... .
... b pn
11.
Положим cij ai1b1 j ai 2b2 j ... aipb pj (i 1,..., m; j 1,..., n) .Матрица
c11 c12 ... c1n
c21 c22 ... c2 n
C
... ... ... ...
c
c
...
c
mn
m1 m 2
называется произведением матрицы А на матрицу В и обозначается А∙В.
12.
Замечание. Размерность произведения матриц можно определить поправилу, которое в дальнейшем будет называться правилом умножения
размерностей: (m р)( р п) m п .
2 1
Пример 3 . Пусть A
4 2
матриц А∙В и В∙А.
0 5
и B 3 1 . Найти произведение
13.
Решение2 1 0 5 2 0 1 3 2 5 1 1 3 9
,
A B
4 2 3 1 4 0 2 3 4 5 2 1 6 18
0 1 5 2 20 10
0 5 2 1 0 2 5 4
.
B A
3 1 4 2 3 2 1 4 3 1 1 2 2 1
14.
Таким образом, мы можем сделать важный вывод: при перемноженииматриц нельзя менять порядок сомножителей (произведение матриц не
коммутативно).
3 4
2 4 1
и В 1 5 .
Пример 4. Даны матрицы А
2 0
1 2 5
Найти произведение А∙В.
15.
Решение.Матрица А имеет размерность 2 3, матрица В – размерность 3 2.
Следовательно, можно умножить А на В. По правилу умножения
размерностей (2 3)(3 2) 2 2 . Матрица С=АВ будет иметь размерность 2 2:
с11
С
с21
3 4
2 3 4 1 1 2
с12 2 4 1
2 4 4 5 1 0
1 5
с22 1 2 5
1 3 2 1 5 2 1 4 2 5 5 0
2 0
6 4 2 8 20 12 12
.
6
3 2 10 4 10 15
Задание 1. Проверить можно ли найти произведение ВА. Если возможно,
найдите его.
16.
Свойства операции умножения матриц:1) Произведение матриц, если оно имеет смысл, ассоциативно, т.е.
A( BC) ( AB )C ;
2) Произведение матриц дистрибутивно относительно сложения, т.е.
A( B C ) AB AC ;
( A B)C AC BC ;
3) AE EA A для любой квадратной матрицы A .
17.
Задание 2. Найти произведение матриц4 3
1. A
2 5
0 1 7
В
2 6 4
8 3
2. С 4 1
0 5
D 9 2
3. M 1 2 3 4
5
6
N
7
8
18.
Задание 3. Найти произведение трех матриц7 2
3 2
3 ,
1. A
, В 0
1 4
1 6
С 3 3 1
1
0 1 7
, В 2 ,
2. А
0
2 6 4
5
С 3 2
19.
2.4. Транспонирование матрица11
Рассмотрим
произвольную матрицу Определение 6. Матрица AТ a12
а11
а21
A
.
а
m1
а12
а22
.
аm 2
... а1n
... а2 n
... .
... аmn
.
a
1n
а 21
a 22
.
a2n
... а m1
... a m 2
,
... .
... a mn
получающаяся из A заменой строк столбцами,
называется транспонированной к A .
2 4 1
Пример 5. Дана матрица А 1 2 5 , найти матрицу АТ.
20.
3. Обратная матрицаОпределение 7. Квадратная матрица A 1 называется обратной к матрице
A , если имеет место равенство: A А 1 А 1 A E.
Не всякая квадратная матрица имеет обратную матрицу.
Определение 8. Квадратная матрица A называется невырожденной, если
ее определитель отличен от нуля, и вырожденной в противном случае.
21.
Теорема 1. Для того чтобы матрица A aij имела обратную матрицу,необходимо и достаточно, чтобы она была невырожденной. При этом обратная
матрица находится по формуле:
A11
1
~
A21
A 1
(A)T , где ~
A
...
detA
A
n1
~
A12
A22
...
An 2
... A1n
... A2 n
.
... ...
... Ann
Матрица A называется присоединенной, элементами этой матрицы являются
алгебраические дополнения соответствующих элементов матрицы А.
22.
Находить обратную матрицу будем по схеме:1. Размерность п п - квадратная матрица
2. А detA 0 - невырожденная матрица
~
3. Найти матрицу A - присоединенная матрица
~T
4. Найти матрицу A - транспонированная матрица
5. Записать матрицу A
1
1 ~T
(A )
detA
23.
1 2. Найти обратную матрицу.
Пример 6. Пусть A
3 4
1 2
2 , матрица имеет обратную. Найдем ее.
Так как detA
3 4
24.
A11 4 , A12 3 , A21 2 , A22 1;~ 4 3
,
A
2 1
1 4 2 2 1
~ T 4 2 ; 1
1 .
3
A
A
2 3 1
3 1
2
2
25.
Задание 4. Заданы матрицы:2 5
1. A
6 3
4 2
2. A
5 7
Найти обратные матрицы
6 5
3. A 4 7
26.
2 1 3Пример 7. Пусть A 2 3 1 . Найти обратную матрицу.
3 2 1
2 1 3
Решение. Так как det A 2 3 1 6 3 12 27 4 2 12 0 матрица
3 2 1
имеет обратную.
27.
Найдем обратную матрицу:3 1
2 1
A11
1 A12
1
2 1
3 1
2 3
A13
5
3 2
1 3
A21
5
2 1
2 3
A22
7
3 1
2 1
A23
1
3 2
1 3
A31
8
3 1
2 3
A32
4
2 1
2 1
A33
4
2 3
28.
1 55 8
5 8
1
1
1
1
~
~Т
1
А 5 7 1 А 1 7 4 A 1 7 4
12
8 4
4
5
1
4
5
1
4
29.
Задание 5. Заданы матрицы:3 5 5
1. A 4 2 1
0
3
3
4 2 1
2. A 5 3 4
2
1
3
Найти обратные матрицы.
6
0 2
3. A 3 1 5
4
2
3
30.
4. Ранг матрицыМинором k -го порядка матрицы A называется определитель,
образованный элементами, расположенными на пересечении каких-либо k
строк и каких-либо k столбцов.
Пусть A - матрица размера m n . Если матрица A нулевая, то ее ранг
равен нулю. Если матрица A ненулевая, то ее рангом называется наибольший
порядок r минора, отличного от нуля.
Пример 8. Вычислим ранг матрицы A , используя определение ранга
матрицы.
5 3 4 1
A 0 2 3 6
5 1 2 11
31.
Ступенчатой матрицей будем называть матрицу, удовлетворяющуюследующим двум условиям:
1) все нулевые строки находятся ниже всех ненулевых;
2) у каждой ненулевой строки, кроме первой, число нулевых элементов,
предшествующих первому ненулевому, больше, чем у предыдущей строки.
32.
Например, ступенчатыми являются матрицы5 4 2
A 0 1 3
0 0 0
6 4
4 1
0
0
3
0
B
0
0
2 1 0 4 5
0 2 1 2 4
0 0
2 5 1
0 0 0 0 0
Частным случаем ступенчатой матрицы является треугольная матрица.
Ранг ступенчатой матрицы равен числу ее ненулевых строк.
В приведенных выше примерах ступенчатых матриц: rang A 2 и
rang В 3.
33.
Ранг матрицы удобно находить, приводя матрицу к ступенчатому виду.Такие преобразования возможно выполнить с помощью элементарных
преобразований матриц.
Элементарные преобразования матрицы:
1) перестановка строк;
2) умножение какой-либо строки на число, отличное от нуля;
3) сложение строк;
4) те же операции со столбцами.
34.
Матрицы,полученные
одна
из
другой
элементарными
преобразованиями, называются эквивалентными.
Эквивалентность матриц А и В обозначается символом ~: А~В.
Элементарные преобразования матрицы не меняют ее ранга.
35.
Задание 4. Найти ранг матрицы2 1
1. A
4
3
3 2 1
2. В
6 4 2
2 0 1
3. С 2 5 2
4 1 3
1
2 3 4
4. D 1 1 0 2
0 1 3 2
36.
ИДЗ:Мустафина Л.М., Яруллина А.Р. Индивидуальные задания по
высшей математике для самостоятельной работы студентов технических
специальностей. Часть I , Изд-во КарТУ, Караганда, 2021.
Раздел 1. Матрицы. Задания 1-7.












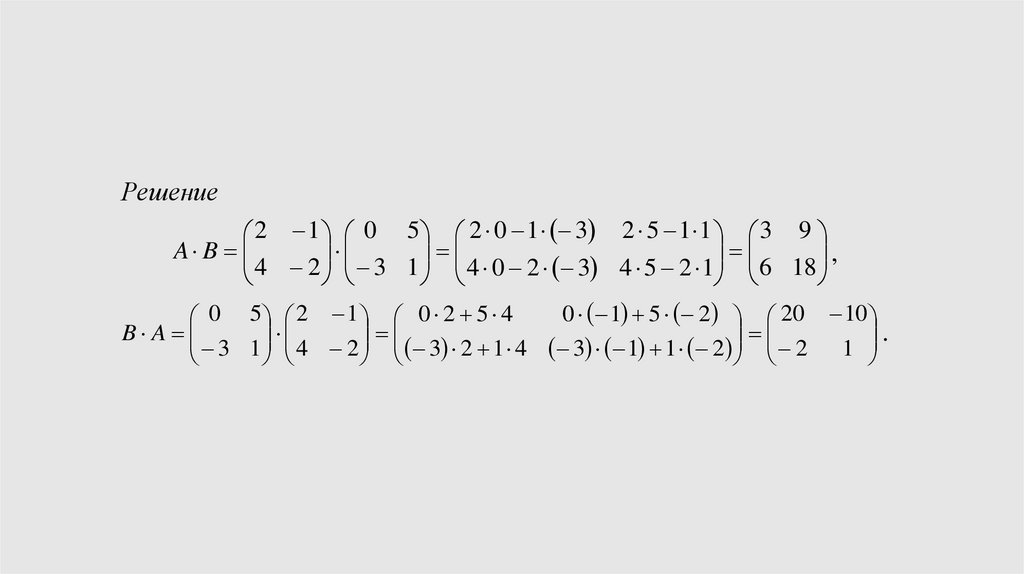










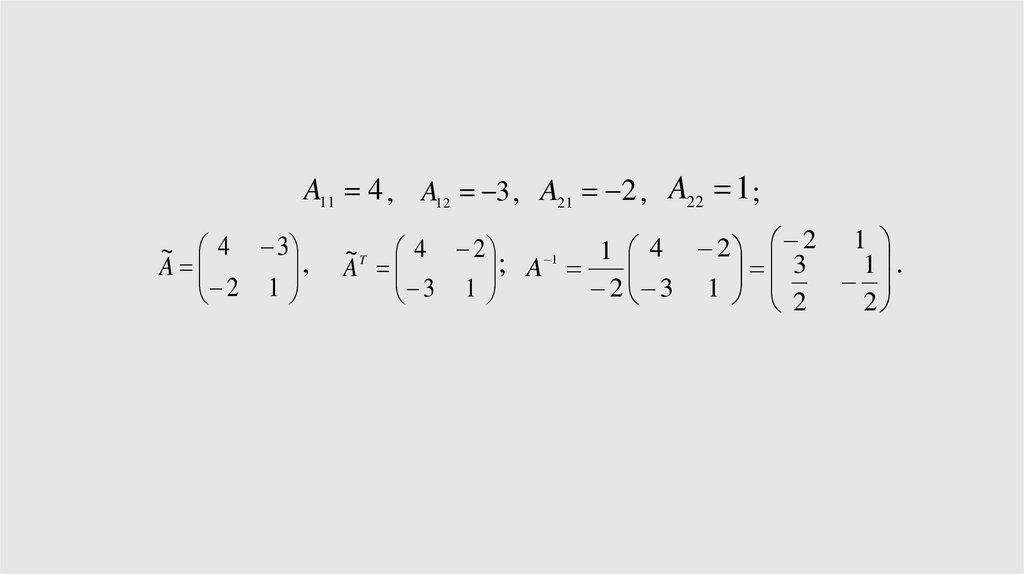



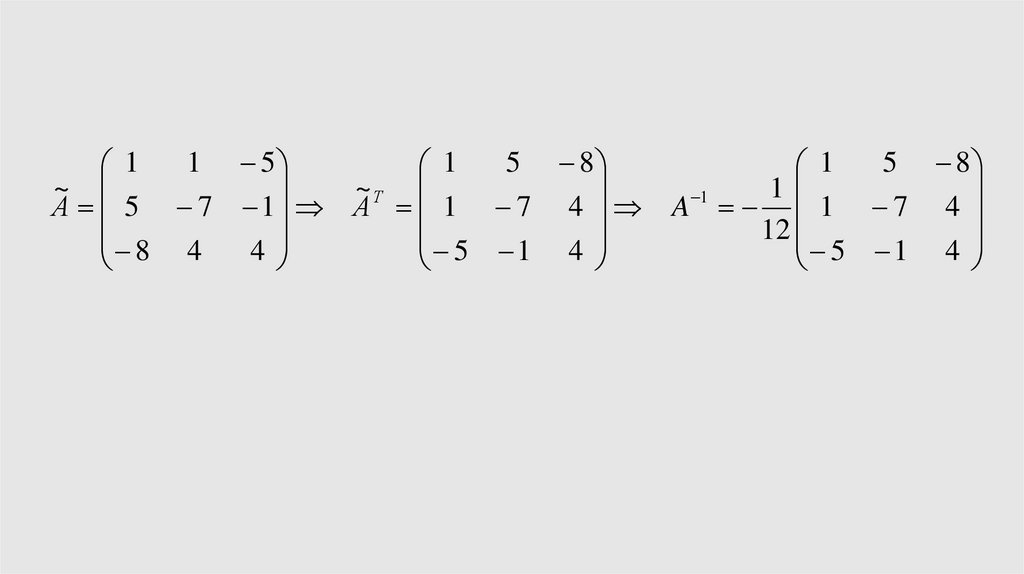








 mathematics
mathematics








