Similar presentations:
Матрицы и действия с ними. Матрицы. Основные понятия. Действия над матрицами
1.
МатематикаЭлементы
линейной
алгебры
Тема 1.
Матрицы. Основные понятия.
Действия над матрицами
Метод обратной матрицы
Презентация 1
2.
Матрицы. Основные понятия.Матрицей называется прямоугольная таблица, составленная из каких – либо элементов
и имеющая m строк и n столбцов.
Элементами матрицы могут быть числа, алгебраические выражения, функции и т.д.
2
a11
a 21
A
a
m1
a12 ... a1n
a 22 ... a 2n
am 2 ... amn
Размерность матрицы обозначается:
Матрицы обозначаются заглавными
буквами латинского алфавита, элементы
матрицы – теми же маленькими буквами.
dim A m n
количество
столбцов
количество
строк
3.
Матрицы. Основные понятия.Если m n , то матрица называется прямоугольной.
Если m n , то матрица называется квадратной (n - ного порядка).
Любое число (скаляр) можно представить как матрицу первого порядка, размерностью 1 1 .
3
Матрица типа 1 n
называется матрица-строка:
Матрица типа m 1 называется матрица-столбец:
a a
11
12
a11
a 21
...
a
m1
a13 ... a1n
4.
Матрицы. Основные понятия.Квадратная
матрица
называется
единичной,
если
ее
элементы,
расположенные на главной диагонали,
равны единице, остальные – нулю
(обозначается буквой Е):
1 0 0
E 0 1 0
0 0 1
Если
все
элементы
квадратной
матрицы
равны
нулю,
то
она
называется
нуль-матрицей
и
обозначается символом 0.
0 0 0
O 0 0 0
0 0 0
4
5.
Матрицы. Основные понятия.Для каждой квадратной матрицы n - ного порядка существует определитель n - ного
порядка, элементы которого равны соответствующим элементам матрицы.
5
a11 a12
A a 21 a 22
a
31 a32
a13
a 23
a33
a11 a12
det A a 21 a 22
a31 a32
a13
a 23
a33
Определитель любой единичной матрицы равен единице.
Если определитель матрицы равен нулю, то матрица называется вырожденной, в
противном случае матрица невырожденная.
6.
Действия над матрицами.Равенство матриц
Матрицы равны, если они имеют
одинаковую размерность и их
соответствующие элементы равны.
A B
dim A dim B; aij bij
6
Сложение (вычитание) матриц
Сумма и разность матриц
существуют только для матриц
одинакового размера, при этом
соответствующие элементы матриц
складываются или вычитаются.
C A B
dim A dim B dim C
c ij aij bij
7.
Действия над матрицами.Умножение матрицы на число
При умножении матрицы A на
число k получается матрица того
же размера, при этом каждый
элемент матрицы A умножается
на k.
B k A
dim A dim B; bij aij k
7
Найти значение выражения:
C A 5 B
1 3 2
A
0 1 4
2 4 1
B
5 0 2
3 5 ( 4) 2 5 1 11 17 7
1 5 2
C
25
1
14
0 5 ( 5) 1 5 0 4 5 2
8.
Действия над матрицами.Умножение матриц
8
Произведение матриц A * B определено
только тогда, когда число столбцов
матрицы А равно числу строк матрицы В,
в противном случае произведение не
существует.
dim A m n
dim B n k
C A B существует
dimC m k
Произведением матрицы A размера [m n] с элементами aij на матрицу B
размера [n k ] с элементами bjq называется матрица C размера [m k ] с элементами:
n
c iq aij b jq
j 1
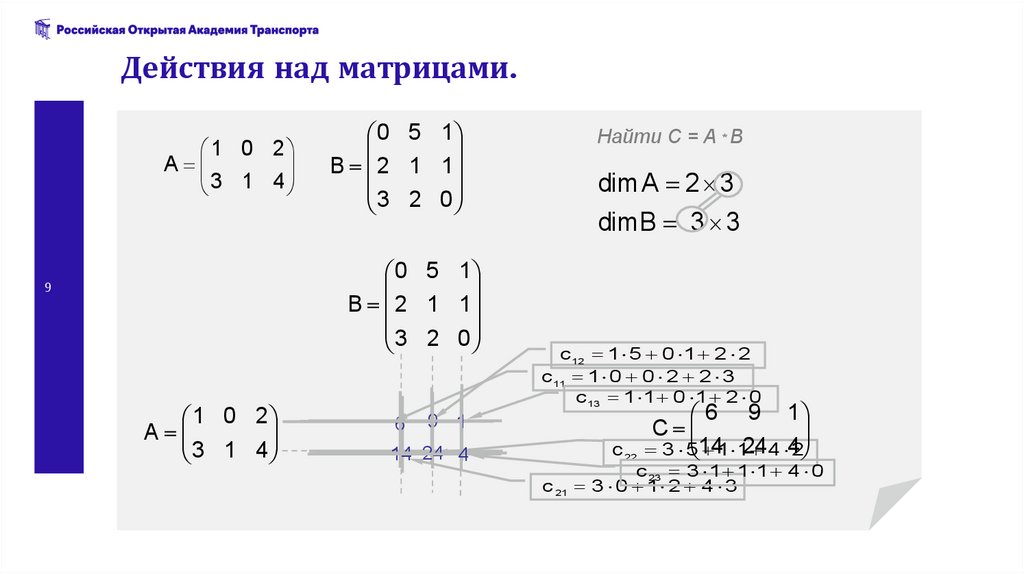
9.
Действия над матрицами.1 0 2
A
3
1
4
0 5 1
B 2 1 1
3 2 0
0 5 1
B 2 1 1
3 2 0
9
1 0 2
A
3
1
4
6
9 1
14 24 4
Найти С = A * B
dim A 2 3
dim B 3 3
c 12 1 5 0 1 2 2
c 11 1 0 0 2 2 3
c 13 1 1 0 1 2 0
6 9 1
C
14
24
4
3 5 1 1 4 2
c 22
c 23 3 1 1 1 4 0
c 21 3 0 1 2 4 3
10.
Действия над матрицами.Свойства операции произведения матриц:
10
1)
A BC AB C ;
2)
AB A B ;
3)
A B C AC BC ;
4)
В общем случае для произведения
матриц не действует переместительный
закон:
A B B A
Иногда АВ существует, а ВА не
имеет смысла. В случае, когда
АВ = ВА, матрицы А и В называются
коммутативными.
5)
Единичная матрица является коммутативной
для любой квадратной матрицы того же
порядка:
EA AE A
6)
Для двух квадратных матриц А и В одного порядка
произведение определителей равно определителю
произведения .
det A det B det AB
11.
Действия над матрицами.Нахождение обратной матрицы
Обратной матрицей по отношению к данной невырожденной квадратной матрице A
n - ного порядка, называется матрица, которая, будучи умноженной как слева, так и
справа на данную матрицу, дает единичную матрицу.
11
Обратная матрица обозначается символом А-1. Таким образом, согласно определению:
АА-1 = А-1А = Е.
A det A 0
AT A
1
A
A
det A
1
Присоединенная матрица получается путем замены
Транспонированная
матрицаматрицы
получается
изего
каждого элемента
Ат Если
на
определитель матрицы равен нулю, то
матрицыалгебраическое
А путем замены
строк
дополнение
обратная матрица не существует
соответствующими столбцами
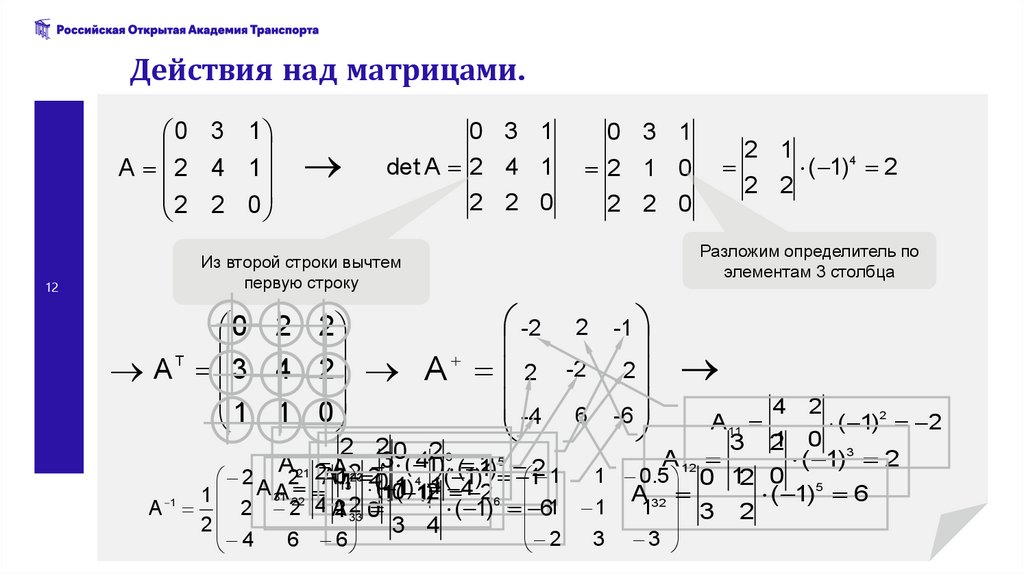
12.
Действия над матрицами.0 3 1
A 2 4 1
2 2 0
12
0 3 1
det A 2 4 1
2 2 0
0 3 1
2 1 0
2 2 0
2 1
( 1)4 2
2 2
Разложим определитель по
элементам 3 столбца
Из второй строки вычтем
первую строку
-2
0 2 2
T
A 3 4 2 A 2
1 1 0
-4
-1
2
2
4 2
-6
A
( 1) 2
1
0
3 2
-2
6
2
11
2 2 0 23
5
A 12
( 1)3 2
3 ( 41) ( 1
A 21 2 A 2
2
4) 2
( 41) 1 1 1 0.5 0 12 0 5
0
113
4 4
2 A 2 A
23 20
1
1
1
(
)
0
2
A
(
1
)
26
31
A 32
( 1) 6
1
1
1
1
1 3 2
A 1 2 222 4 A
2
(
1
)
6
12
0
33
2
3 4
4
6
6
2
3
3
13.
Метод обратной матрицы решения системлинейных уравнений
Метод обратной матрицы рассмотрим на примере решения квадратной системы
3 порядка.
13
a11x1 a12 x 2 a13 x 3 b1
a 21x1 a 22 x 2 a 23 x 3 b 2
a x a x a x b
33 3
3
31 1 32 2
Запишем эту систему в матричном виде. Обозначим:
a11 a12
A a 21 a 22
a
31 a32
a13
a 23
a33
x1
X x2
x3
Матрицаматрица
- столбец
Матрица
- столбец
Основная
системы
неизвестныхсвободных членов
b1
B b2
b3
14.
Метод обратной матрицы решения системлинейных уравнений
Тогда систему можно записать так:
a11 a12
A X a 21 a 22
a
31 a32
a13 x1 a11x1 a12 x 2 a13 x 3 b1
a 23 x 2 a 21x1 a 22 x 2 a 23 x 3 b 2
a33 x 3 a31x1 a32 x 2 a33 x 3 b3
14
Найдем решение системы в матричном виде.
Предположим, что det A отличен от нуля и, следовательно, существует
обратная матрица А-1.
Умножим слева матричную запись системы на обратную матрицу:
A 1 A X A 1 B
E X A 1 B
X A 1 B
Метод обратной матрицы применим для решения квадратных систем с невырожденной
основной матрицей.
A X B
15.
Метод обратной матрицы решения системлинейных уравнений
Решить систему методом обратной матрицы.
15
3 x 2 x 3 1
2x1 4 x 2 x 3 2
2x 2x 3
2
1
X A 1 B
1 0 .5
1
1
A 1 1
1
2
3 3
0 3 1
A 2 4 1
2 2 0
x1
X x2
x3
1
B 2
3
1
B 2
3
-0,5
2
-5
0 .5
X 2
5













 mathematics
mathematics








