Линейная алгебра. Матрицы. Основные понятия. Действия над матрицами. Поиск обратной матрицы

1. Линейная алгебра

Матрицы. Основные понятия.
Действия над матрицами
Поиск обратной матрицы

2. Матрицы. Основные понятия

Матрицей называется прямоугольная таблица, составленная
из каких – либо элементов и имеющая m строк и n столбцов.
Элементами матрицы могут быть числа, алгебраические
выражения, функции и т.д.
a11
a 21
A
a
m1
a12
a 22
am 2
a1n
... a 2n
... amn
...
Матрицы обозначаются заглавными буквами латинского алфавита,
элементы матрицы – теми же маленькими буквами.
Размерность матрицы обозначается:
dim A m n
количество
количество
строк столбцов

3. Матрицы. Основные понятия

Если m n , то матрица называется прямоугольной.
Если m n
порядка).
, то матрица называется
квадратной (n - ного
Любое число (скаляр) можно представить как матрицу первого
порядка, размерностью 1 1 .
Матрица типа 1 n называется матрица-строка:
a
11
a12 a13 ... a1n
Матрица типа m 1 называется матрица-столбец:
a11
a 21
...
a
m1

4. Матрицы. Основные понятия

Квадратная матрица называется единичной, если ее элементы,
расположенные на главной диагонали, равны единице,
остальные – нулю (обозначается буквой Е):
1 0 0
E 0 1 0
0 0 1
Если все элементы квадратной матрицы равны нулю, то она
называется нуль-матрицей и обозначается символом 0.
0 0 0
O 0 0 0
0 0 0

5. Матрицы. Основные понятия

Для каждой квадратной матрицы n - ного порядка существует
определитель n - ного порядка, элементы которого равны
соответствующим элементам матрицы.
a11 a12
A a 21 a 22
a
31 a 32
a13
a 23
a 33
a11
a12
a13
det A a 21 a 22
a 23
a 31
a 32
a 33
Определитель любой единичной матрицы равен единице.
Если определитель матрицы равен нулю, то
называется вырожденной, в противном случае
невырожденная.
матрица
матрица

6. Действия над матрицами

Равенство матриц
Матрицы равны, если они имеют одинаковую размерность и их
соответствующие элементы равны.
A B
dim A dimB;
1
7
81, 2
3
A
16
3
0
sin(2 1) 45 53
aij bij
1
7
81, 2
3
B
16
3
0
sin(2 1) 45 53

7. Действия над матрицами

Сложение (вычитание) матриц
Сумма и разность матриц существуют только для матриц
одинакового размера, при этом соответствующие элементы
матриц складываются или вычитаются.
C A B
dim A dimB dimC
c ij aij bij
7 4 1
2 0 1
A 4 3 0 B 1 2 7
3 2 8
4 4 3
9 4 0
C 5 5 7
1 6 5

8. Действия над матрицами

Умножение матрицы на число
При умножении матрицы A на число k получается матрица того же
размера, при этом каждый элемент матрицы A умножается на k.
B k A
dim A dimB; bij aij k
Найти значение выражения: C A 5 B
1 3 2
A
0 1 4
2 4 1
B
5 0 2
3 5 ( 4) 2 5 1 11 17 7
1 5 2
C
0 5 ( 5) 1 5 0 4 5 2 25 1 14

9. Действия над матрицами

Умножение матриц
Произведение матриц A * B определено только тогда, когда
число столбцов матрицы А равно числу строк матрицы В, в
противном случае произведение не существует.
dim A m n
dim B n k
C A B существует
dimC m k
Произведением матрицы A размера [m n] с элементами aij
на матрицу B размера [n k ] с элементами bjq называется
матрица C размера [m k ] с элементами:
n
c iq aij b jq
j 1

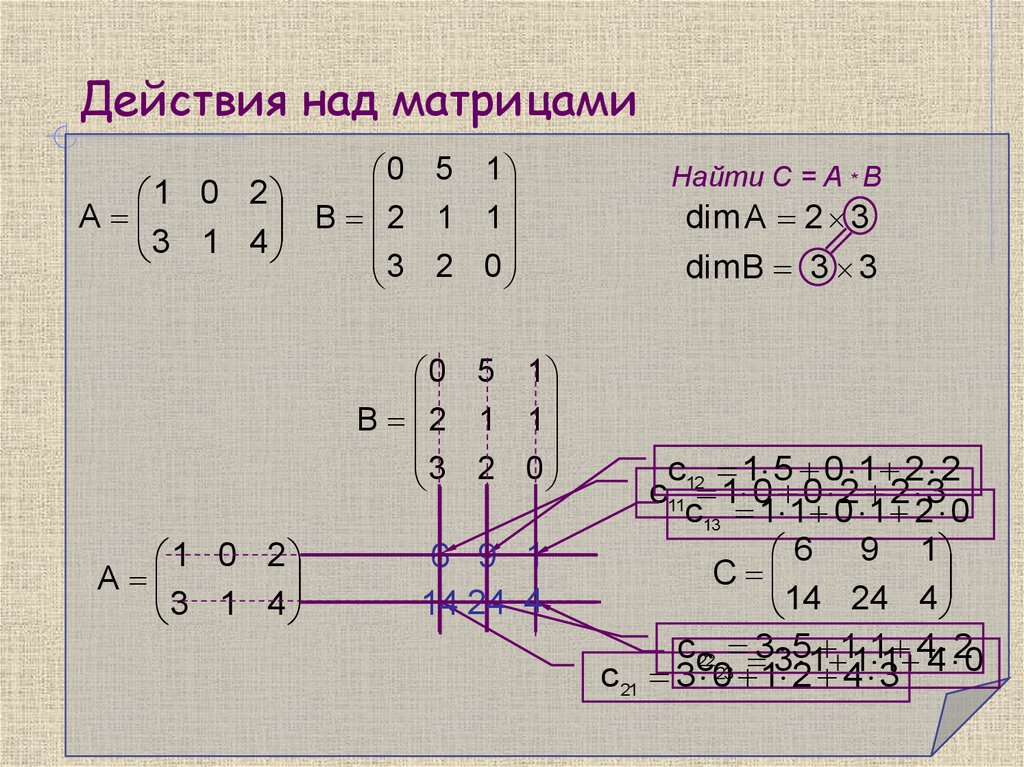
10. Действия над матрицами

1 0 2
A
3 1 4
0 5 1
B 2 1 1
3 2 0
0 5 1
B 2 1 1
3 2 0
1 0 2
A
3 1 4
6 9 1
14 24 4
Найти С = A * B
dim A 2 3
dimB 3 3
c12 1 5 0 1 2 2
c11 1 0 0 2 2 3
c13 1 1 0 1 2 0
6 9 1
C
14 24 4
cc22 33 5 1 11 1
44 20
1
c 21 3 023 1 2 4 3

11. Действия над матрицами

Свойства операции произведения матриц:
A BC AB C ;
2) AB A B ;
3) A B C AC BC ;
1)
4) В общем случае для произведения матриц не действует
переместительный закон: A B B A
иногда АВ существует, а ВА не имеет смысла. В случае, когда
АВ = ВА, матрицы А и В называются коммутативными.
5) Единичная матрица является коммутативной для любой
квадратной матрицы того же порядка:
EA AE A
6) Для двух квадратных матриц А и В одного порядка произведение
определителей равно определителю произведения .
det A det B det AB

12. Действия над матрицами

Нахождение обратной матрицы
Обратной матрицей по отношению к данной невырожденной
квадратной матрице A n - ного порядка, называется матрица,
которая, будучи умноженной как слева, так и справа на данную
матрицу, дает единичную матрицу.
Обратная матрица обозначается символом А-1. Таким образом,
согласно определению: АА-1=А-1А=Е.
1
A
A A
A det A 0 A
det A
T
1
Транспонированная матрица
Присоединенная матрица
получается из матрицы А Если определитель матрицы
получается путем замены каждого
путем замены строк т
равен нулю, то обратная
элемента матрицы А на его
соответствующими
матрица не существует
алгебраическое дополнение
столбцами

13. Действия над матрицами

0 3 1
0 3 1
0 3 1
2 1
4
(
1
)
2
2
1
0
det
A
2
4
1
A 2 4 1
2 2
2 2 0
2 2 0
2 2 0
0 2 2 Из второй -2
T
A 2
A 3 4 строки
2 вычтем
строку
1 1 первую
0
-4
2 -1
Разложим
-2 2 определитель
по элементам
3 столбца
6 -6
4 2
A 11 3 2
( 1)2 3 2
2 320 42 3 5
A 12 0
1 20 ( 1) 2
2 23
2 2 ( 4 1( 4) (
A 21 A
)14)2 1
0
A
2
1 0( 1)5 6
1
A
13
0
2
AA
(
1
)
4
1 320.5
11) 1 62 1
12 101 (21
31 22
A
(
1
)
6
3 2
1 4331 2 03 4
1
1
A 2 2
2 1 1
2
2
3
3
4
6
6