Правильные многоугольники

1.

Правильные
многоугольники
mathvideourok.moy.su

2.

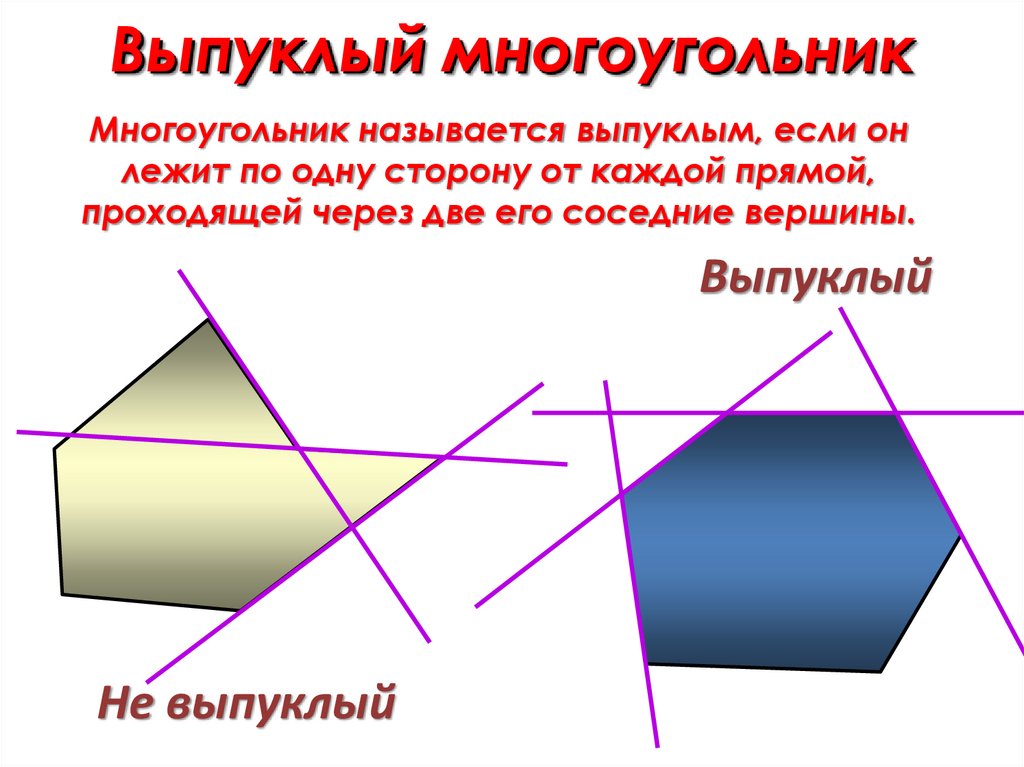
Выпуклый многоугольник
Многоугольник называется выпуклым, если он
лежит по одну сторону от каждой прямой,
проходящей через две его соседние вершины.
Выпуклый
Не выпуклый

3.

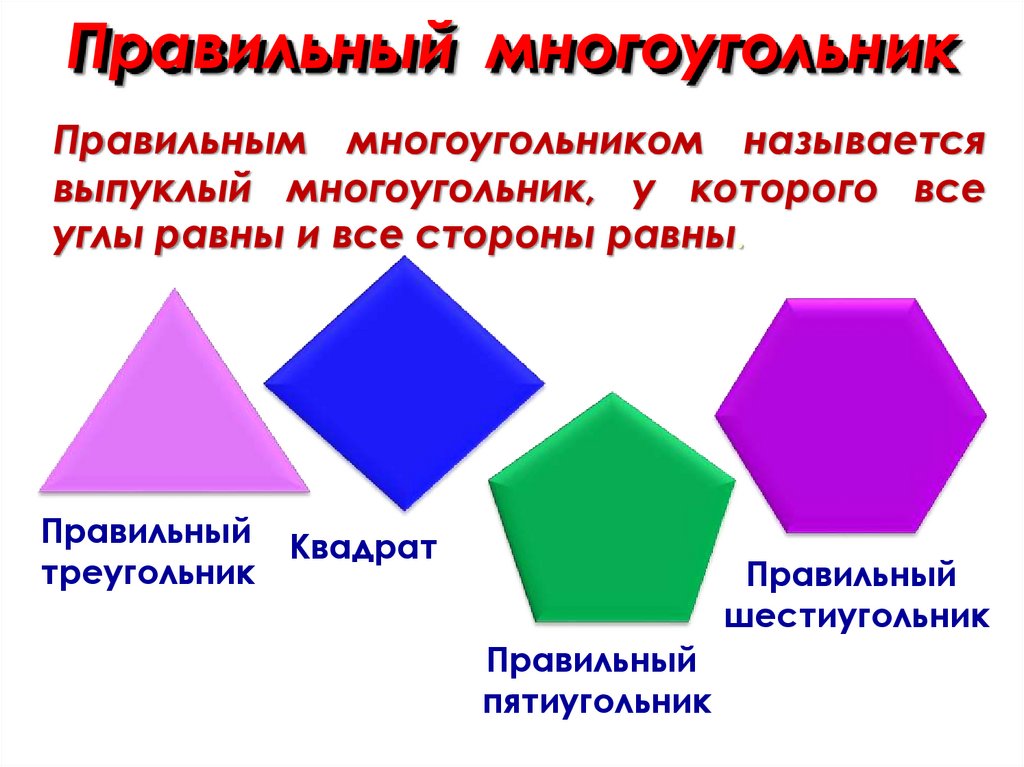
Правильный многоугольник
Правильным многоугольником называется
выпуклый многоугольник, у которого все
углы равны и все стороны равны.
Правильный
треугольник
Квадрат
Правильный
шестиугольник
Правильный
пятиугольник

4.

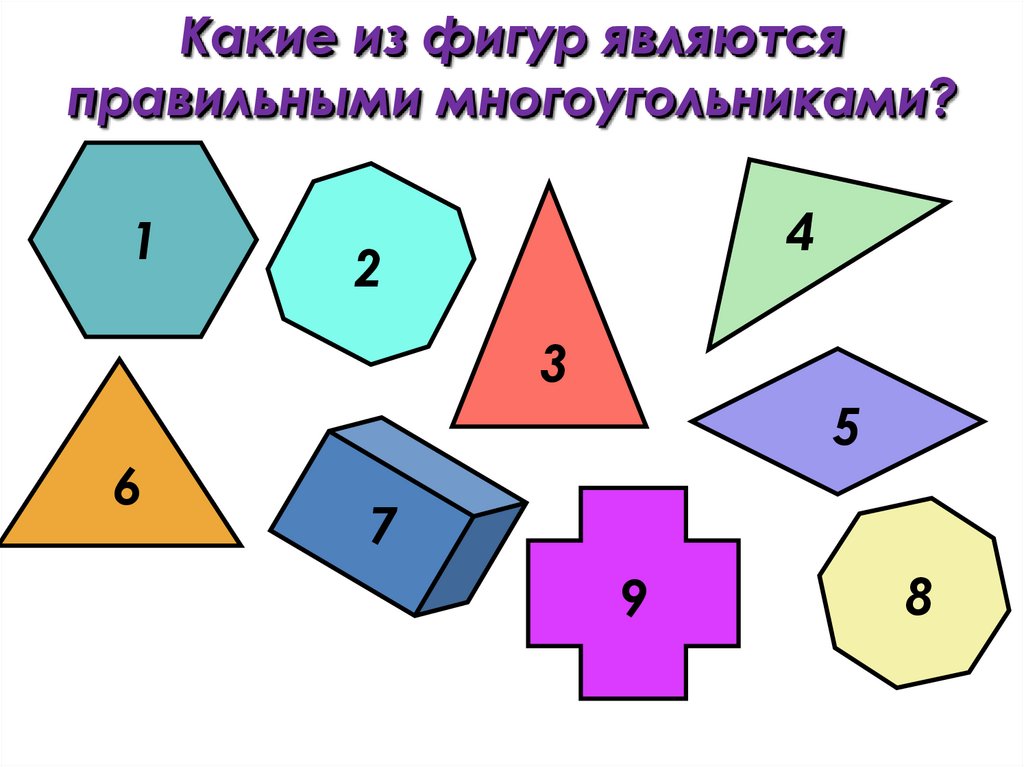
Какие из фигур являются
правильными многоугольниками?
1
4
2
3
6
5
7
9
8

5.

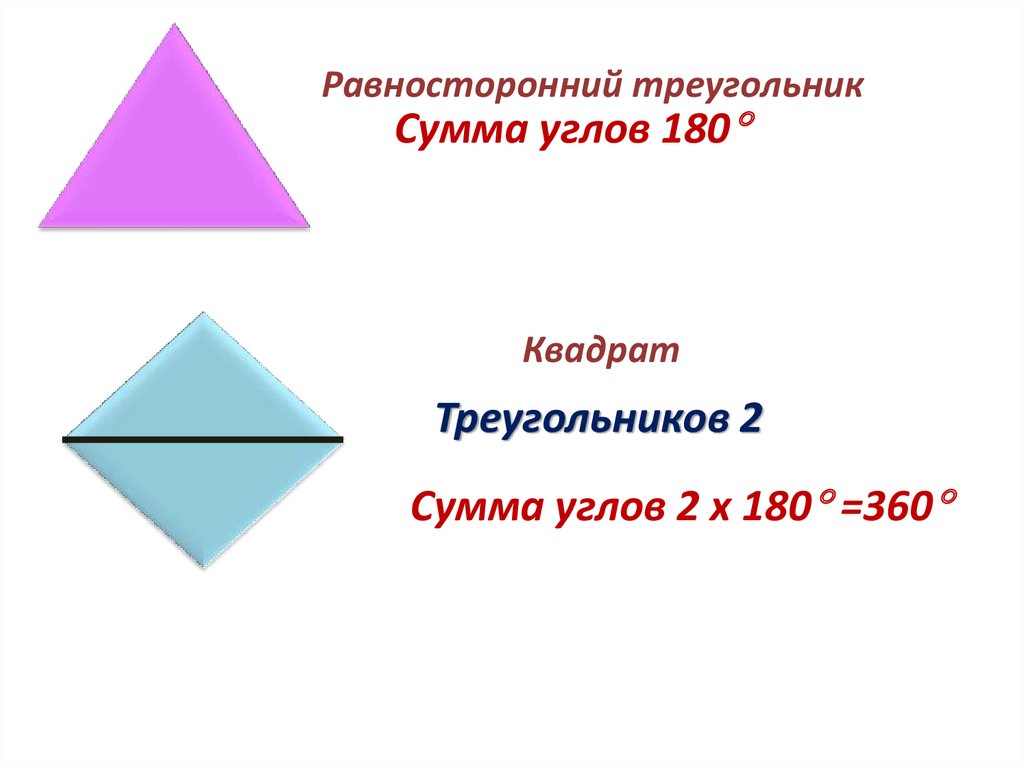
Равносторонний треугольник
Сумма углов 180
Квадрат
Треугольников 2
Сумма углов 2 х 180 =360

6.

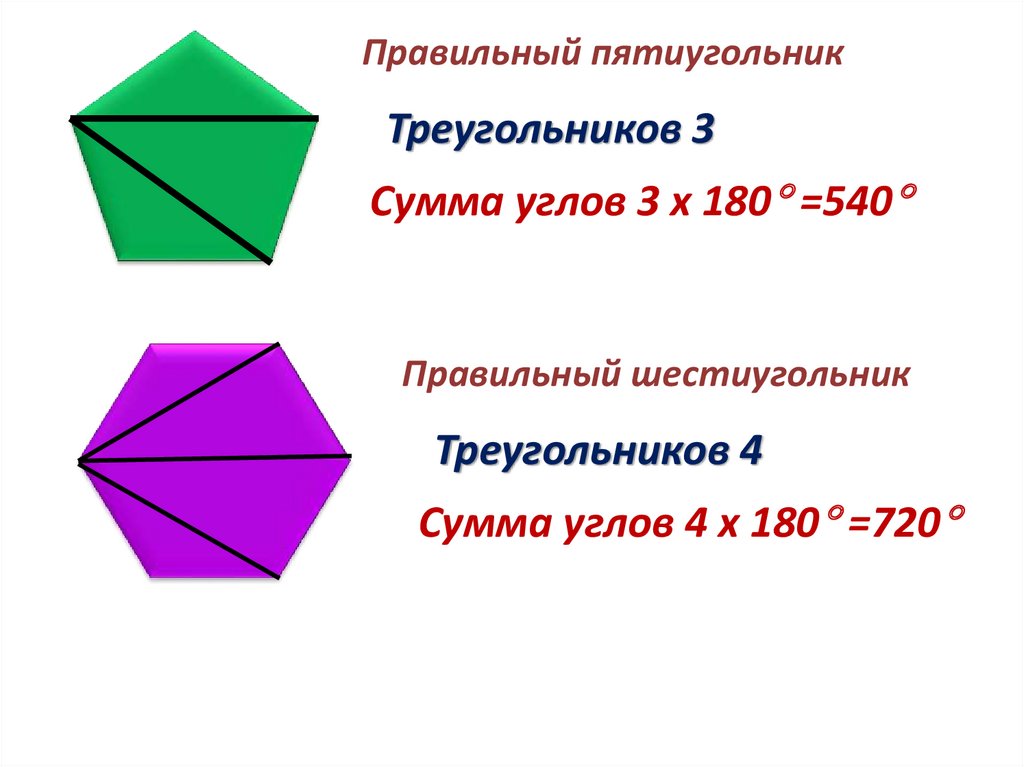
Правильный пятиугольник
Треугольников 3
Сумма углов 3 х 180 =540
Правильный шестиугольник
Треугольников 4
Сумма углов 4 х 180 =720

7.

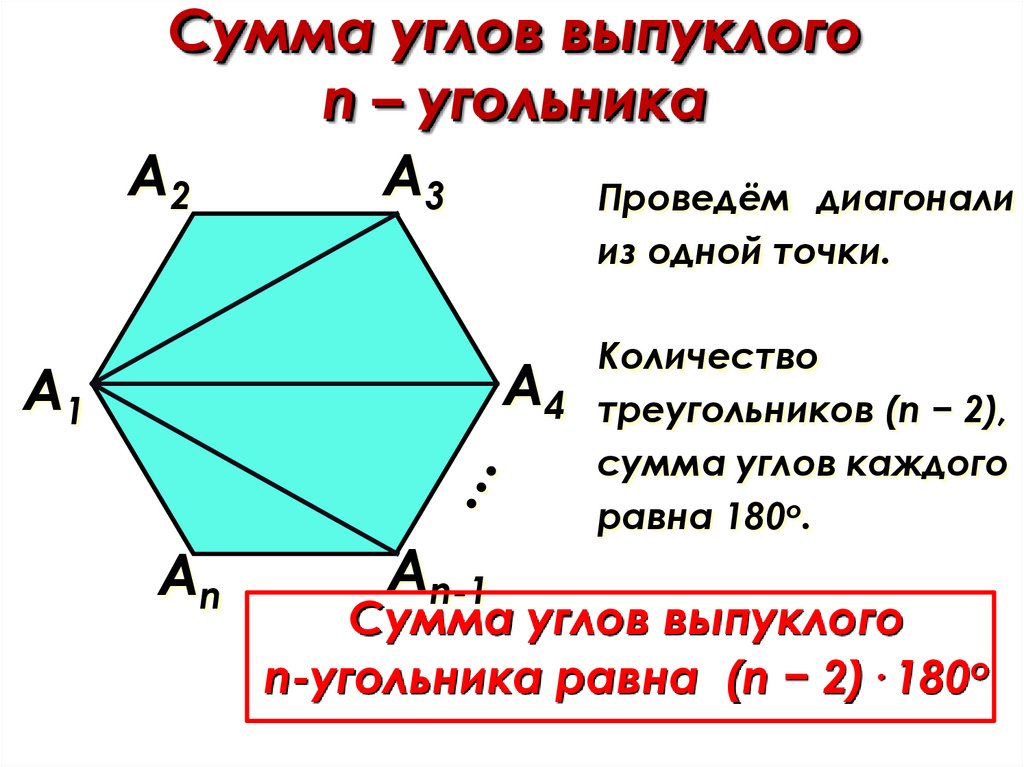
Сумма углов выпуклого
n – угольника
А2
А3
Проведём диагонали
из одной точки.
А1
Аn
Аn-1
Количество
А4 треугольников (n − 2),
сумма углов каждого
равна 180о.
Сумма углов выпуклого
n-угольника равна (n − 2)· 180о

8.

Чтобы найти один из углов
Например
n 2
180
n
6 2
1)п 6, то
180 120
6
2) 144 п ?
п 2
144
180
п 2
п
180
п
п 10

9.

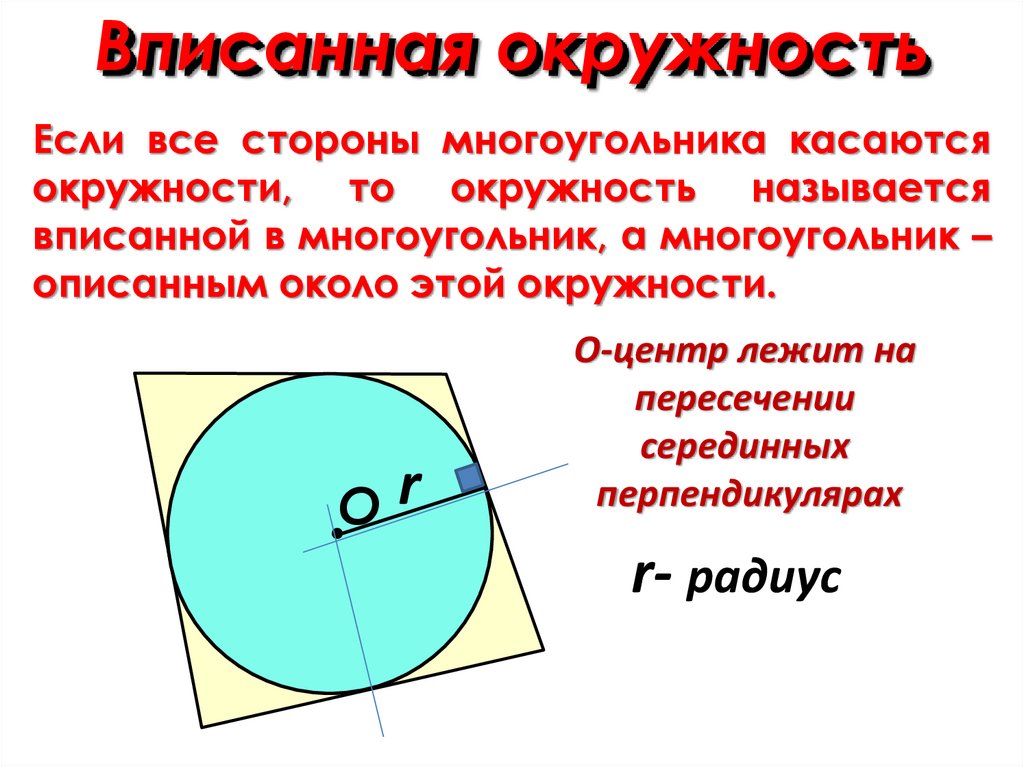
Вписанная окружность
Если все стороны многоугольника касаются
окружности, то окружность называется
вписанной в многоугольник, а многоугольник –
описанным около этой окружности.
r
О
О-центр лежит на
пересечении
серединных
перпендикулярах
r- радиус

10.

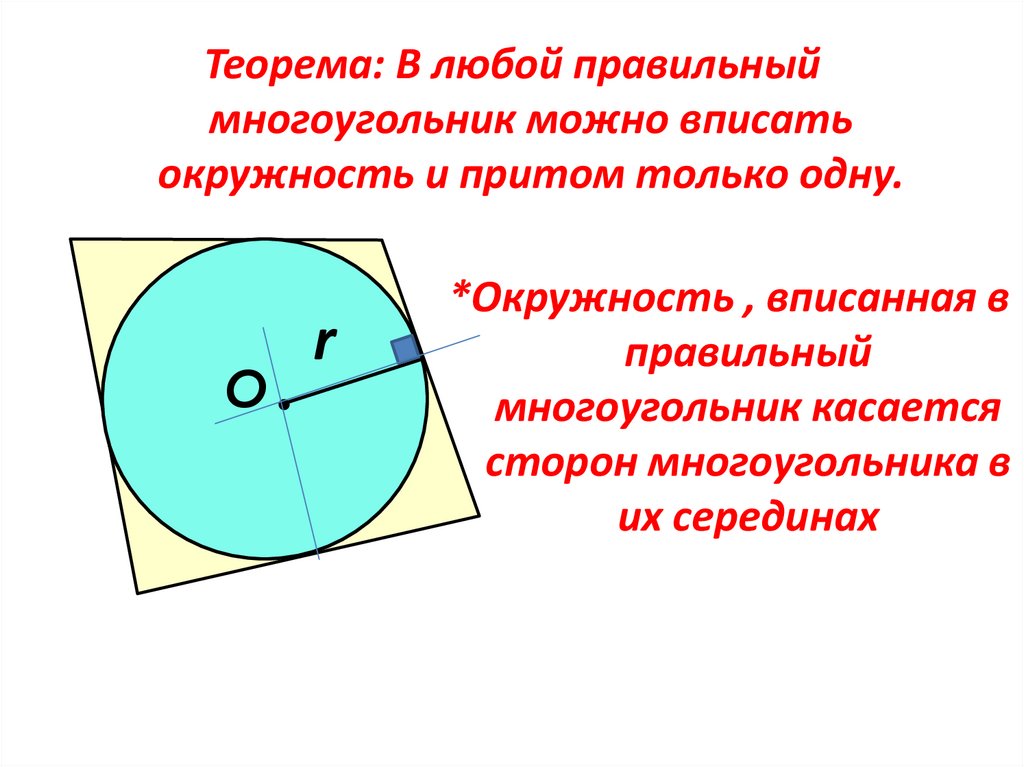
Теорема: В любой правильный
многоугольник можно вписать
окружность и притом только одну.
О
r
*Окружность , вписанная в
правильный
многоугольник касается
сторон многоугольника в
их серединах

11.

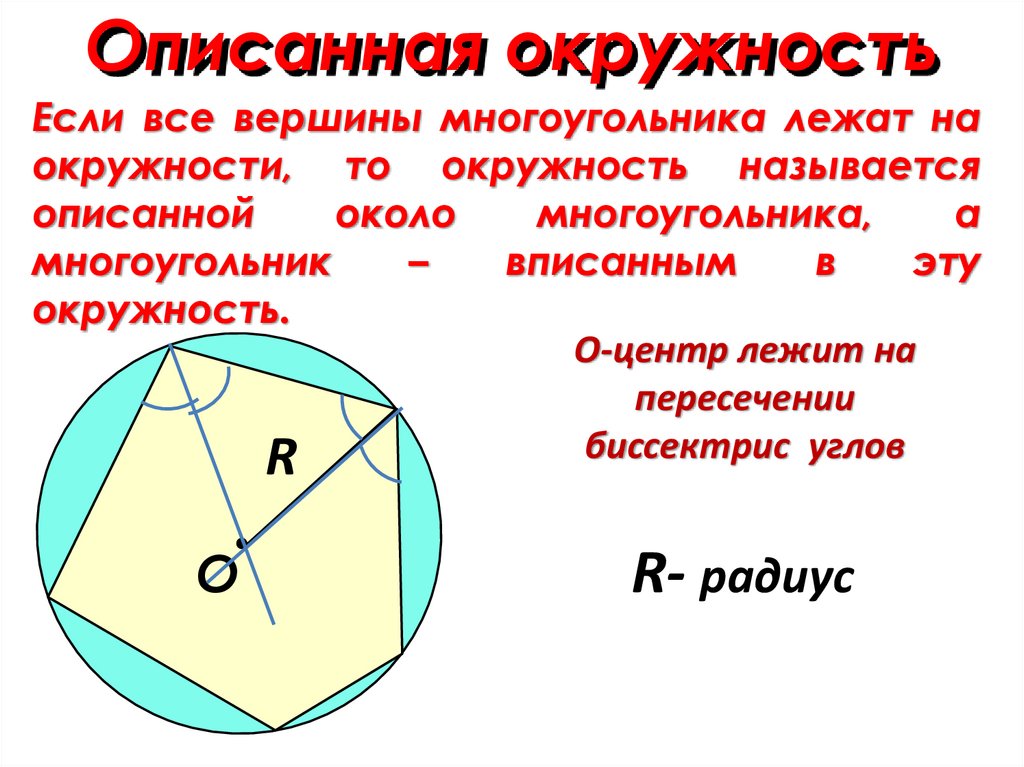
Описанная окружность
Если все вершины многоугольника лежат на
окружности, то окружность называется
описанной
около
многоугольника,
а
многоугольник
–
вписанным
в
эту
окружность.
О-центр лежит на
пересечении
биссектрис углов
R
О
R- радиус

12.

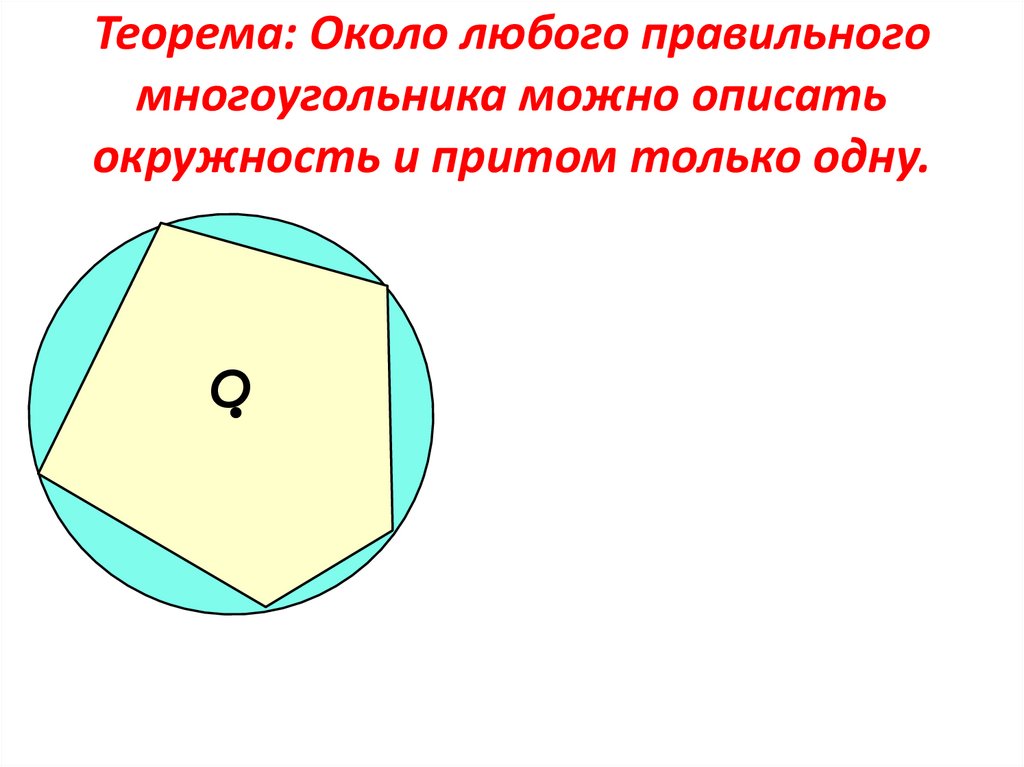
Теорема: Около любого правильного
многоугольника можно описать
окружность и притом только одну.
О

13.

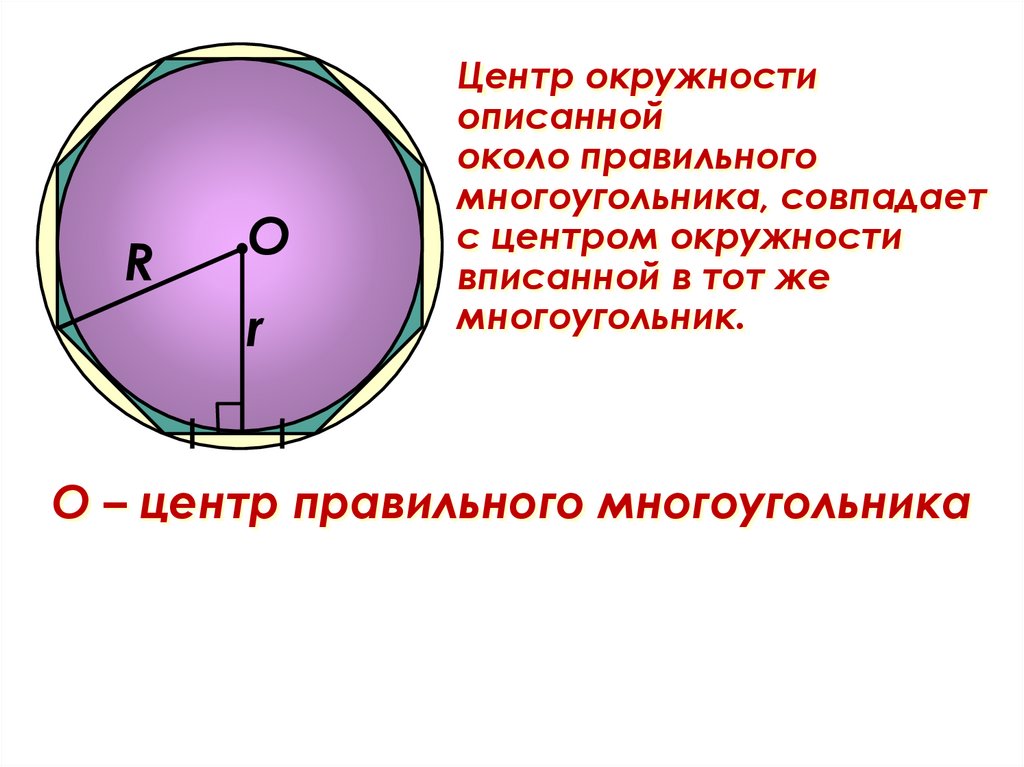
R
О
r
Центр окружности
описанной
около правильного
многоугольника, совпадает
с центром окружности
вписанной в тот же
многоугольник.
О – центр правильного многоугольника

14.

Формула площади правильного
многоугольника
S n S A1OA2
А4
О
R
А1
А3
r
А2
1
n ah
2
1
1
n A1 A2 r Pr
2
2
1
S P r
2
P периметр, r радиус

15.

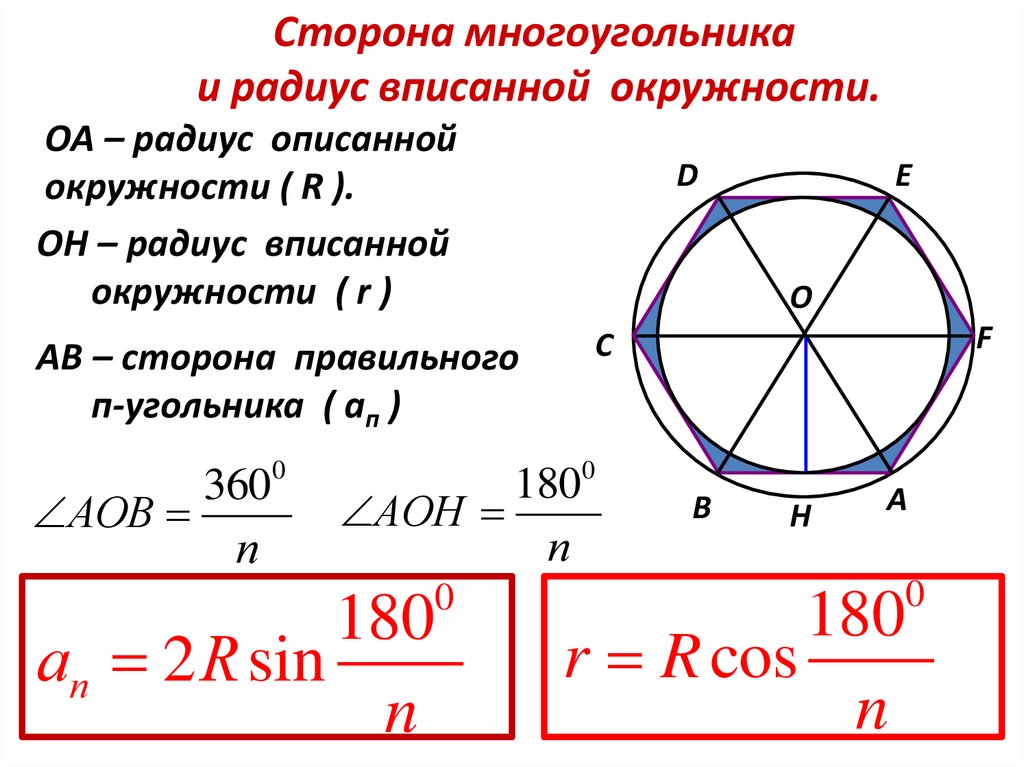
Сторона многоугольника
и радиус вписанной окружности.
ОА – радиус описанной
окружности ( R ).
ОН – радиус вписанной
окружности ( r )
D
О
1800
АОН
п
180
ап 2 R sin
n
0
F
С
АВ – сторона правильного
п-угольника ( ап )
3600
АОВ
п
Е
В
Н
А
180
r R cos
n
0

16.

180
ап 2 R sin
n
0
п=3
0
180
3
0
а3 2 R sin
2 R sin 60 2 R
R 3
3
2
п=4
1800
2
0
а4 2 R sin
2 R sin 45 2 R
R 2
4
2
п=6
0
180
1
0
а6 2 R sin
2 R sin 30 2 R R
6
2

17.

а-сторона многоугольника
n-число
сторон
n=3
n=4
n=6
R
а
3
а
2
а
r
а
2 3
а
2
3
а
2

18.

Построение правильного
шестиугольника, сторона которого
равна данному отрезку.
1.
2.
Построить окружность с
радиусом, равным PQ.
Отметить на окружности
произвольную точку А1.
Т.к. R = PQ, а6 = R, то отметим
на окружности точки А1, А2, А3, А4,
А5, А6 так, чтобы А1А2 = А2А3 = А3А4
=
= А4А5 = А5А6.
4. Последовательно соединить
отрезками полученные точки.
P
Q
А4
А5
3.
А3
А6
А1
А2

19.

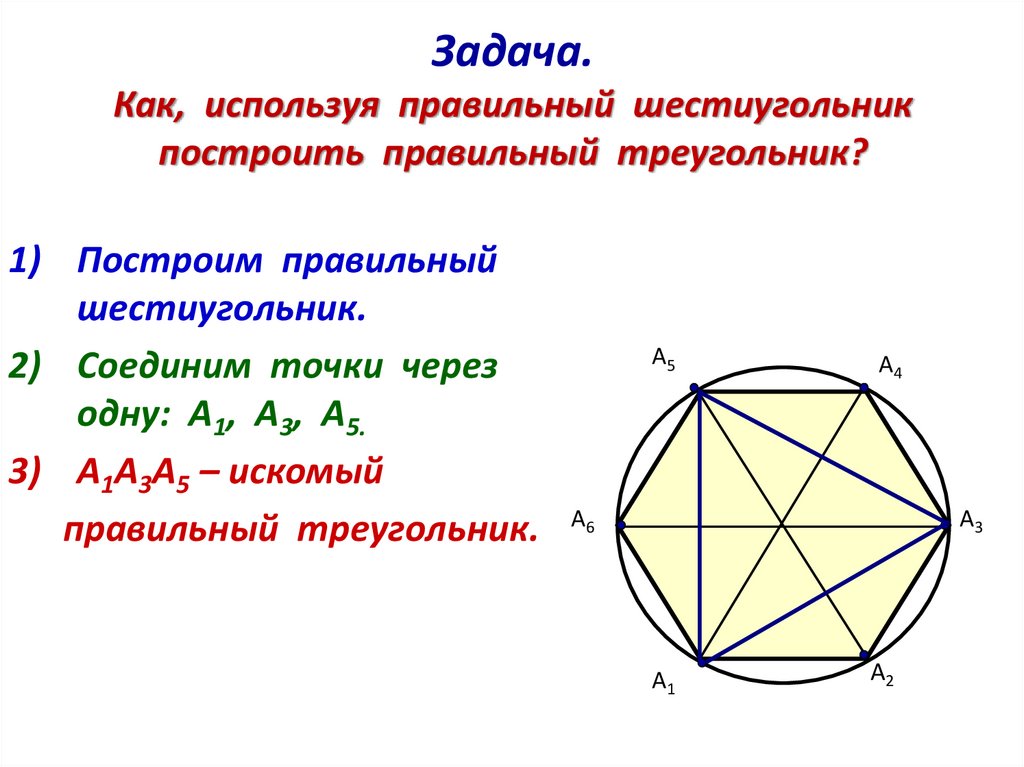
Задача.
Как, используя правильный шестиугольник
построить правильный треугольник?
1) Построим правильный
шестиугольник.
2) Соединим точки через
одну: А1, А3, А5.
3) А1А3А5 – искомый
правильный треугольник.
А5
А4
А6
А3
А1
А2

20.

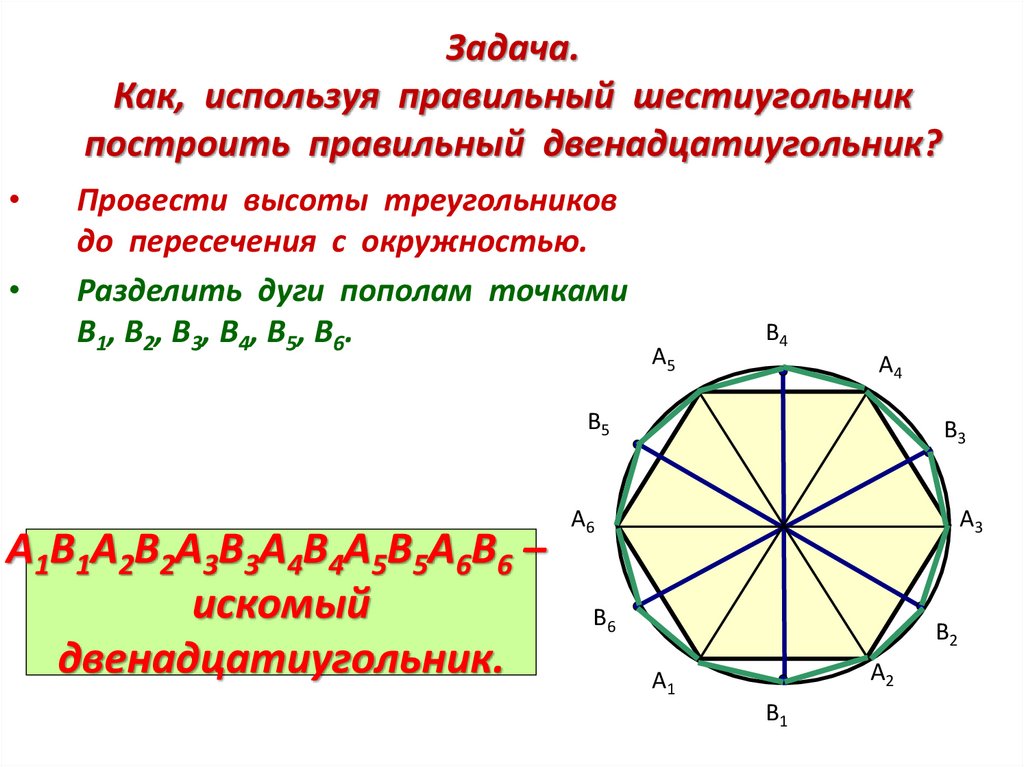
Задача.
Как, используя правильный шестиугольник
построить правильный двенадцатиугольник?
Провести высоты треугольников
до пересечения с окружностью.
Разделить дуги пополам точками
В1, В2, В3, В4, В5, В6.
А5
В4
А4
В5
А1В1А2В2А3В3А4В4А5В5А6В6 –
искомый
двенадцатиугольник.
В3
А6
А3
В6
В2
А2
А1
В1