Выпуклый многоугольник

1.

Геометрия 9 класс

2.

Домашнее задание

3.

Найдите АС:
1.
В
С
45º
А
3
D
АВСD - ромб

4.

АВСD - ромб
Найдите АС:
В
С
1. АDС 135
2. AD CD 3
45º
А
D
3
АС 2 АD 2 СD 2 2 АD СD cos D
АС 3 3 2 3 3 cos 135
2
2
2
АС 2 9 9 18( cos 45 )
АС 2 9(2 2 )
Ответ : AC 3 2 2

5.

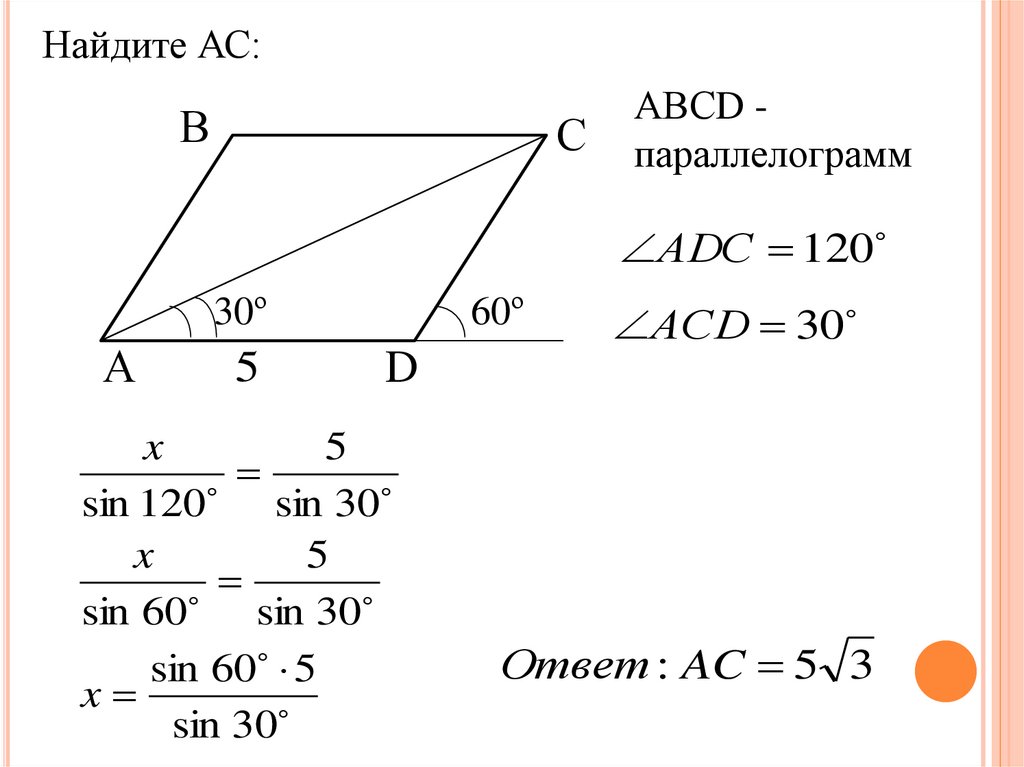
Найдите АС:
2.
В
С
30º
А
5
60º
D
АВСD параллелограмм

6.

Найдите АС:
В
С
АВСD параллелограмм
АDC 120
30º
А
5
60º
АСD 30
D
x
5
sin 120
sin 30
x
5
sin 60
sin 30
sin 60 5
x
sin 30
Ответ : AC 5 3

7.

Правильные
многоугольники

8.

ВЫПУКЛЫЙ МНОГОУГОЛЬНИК
Многоугольник называется выпуклым, если он
лежит в одной полуплоскости относительно любой
прямой, содержащей его сторону.

9.

ПРАВИЛЬНЫЙ
МНОГОУГОЛЬНИК
Выпуклый
многоугольник
называется
правильным , если у него все стороны равны и все
углы равны.
Квадрат
Правильный
треугольник
Правильный
шестиугольник
Правильный
пятиугольник

10.

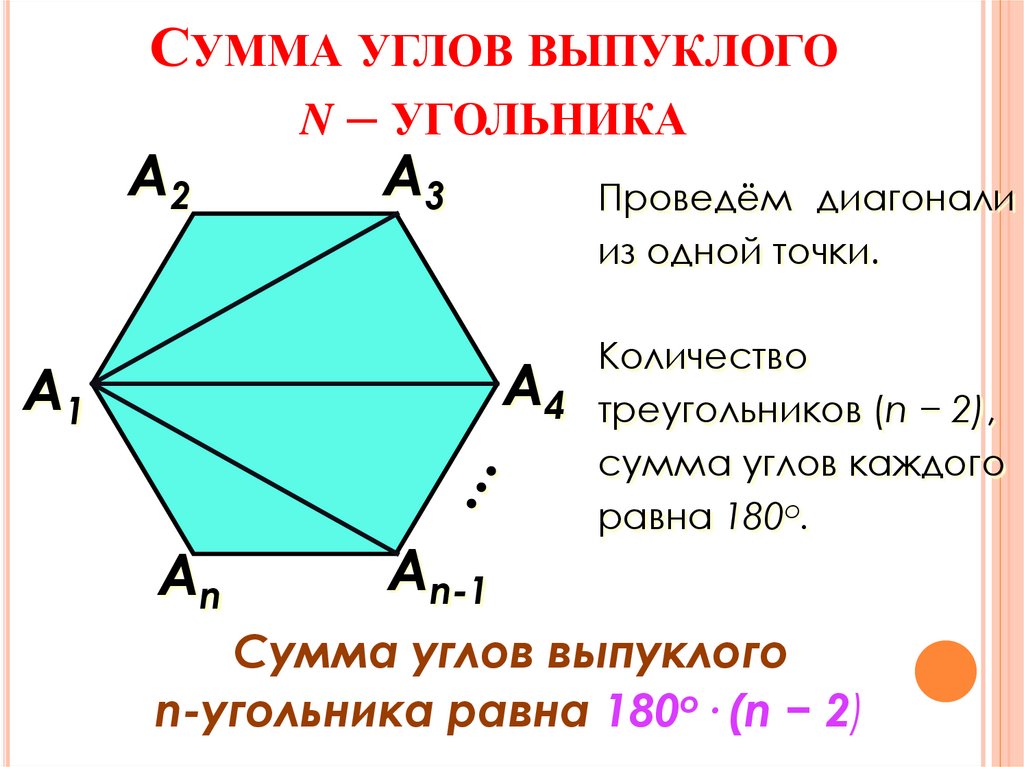
СУММА УГЛОВ ВЫПУКЛОГО
N – УГОЛЬНИКА
А2
А3
Проведём диагонали
из одной точки.
А1
Аn
Аn-1
Количество
А4 треугольников (n − 2),
сумма углов каждого
равна 180о.
Сумма углов выпуклого
n-угольника равна 180о· (n − 2)

11.

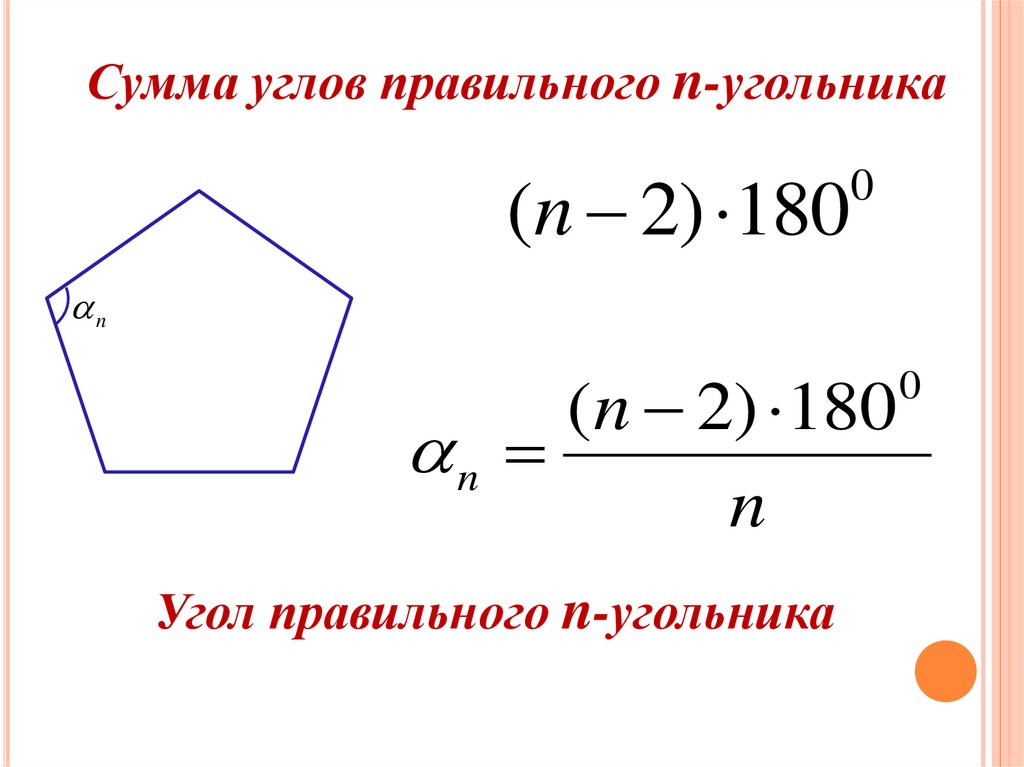
Сумма углов правильного n-угольника
(n 2) 180
0
n
(n 2) 180
n
n
Угол правильного n-угольника
0

12.

Вписанная окружность
Если все стороны многоугольника касаются
окружности, то окружность называется вписанной в
многоугольник, а многоугольник – описанным около
этой окружности.
О

13.

ОПИСАННАЯ ОКРУЖНОСТЬ
Если все вершины многоугольника лежат на
окружности, то окружность называется описанной
около многоугольника, а многоугольник – вписанным в
эту окружности.
О

14.

ТЕОРЕМА ОБ ОКРУЖНОСТИ, ОПИСАННОЙ ОКОЛО ПРАВИЛЬНОГО
МНОГОУГОЛЬНИКА
А2
Около любого правильного
многоугольника можно
описать окружность, и
притом только одну.
А3
А1
А4
О
Аn
Аn -1

15.

ТЕОРЕМА ОБ ОКРУЖНОСТИ, ВПИСАННОЙ
В ПРАВИЛЬНЫЙ
МНОГОУГОЛЬНИК
А2
В любой правильный
многоугольник можно
вписать окружность, и
притом только одну.
А3
А1
А4
О
Аn
Аn -1

16.

R
О
Следствие1
Окружность, вписанная в
правильный многоугольник,
касается сторон
многоугольника
в их серединах.
r
Следствие 2
Центр окружности описанной
около правильного
многоугольника, совпадает с
центром окружности
вписанной в тот же
многоугольник.
О – центр правильного многоугольника

17.

ЗАДАЧИ
НА ПОСТРОЕНИЕ
ПРАВИЛЬНЫХ
МНОГОУГОЛЬНИКОВ

18.

ПОСТРОЕНИЕ ПРАВИЛЬНОГО ШЕСТИУГОЛЬНИКА,
СТОРОНА КОТОРОГО РАВНА ДАННОМУ ОТРЕЗКУ.
1. Построить окружность с радиусом,
равным PQ.
2. Отметить на окружности
произвольную точку А1.
3. Т.к. R = PQ, а6 = R, то отметим на
окружности точки А1, А2, А3, А4, А5,
А6 так, чтобы
А1А2 = А2А3 = А3А4 = А4А5 = А5А6.
4. Последовательно соединить
отрезками полученные точки.
А1А2А3А4А5А6 –
Q
P
А4
А5
А3
А6
искомый шестиугольник.
А2
А1

19.

ЗАДАЧА.
КАК, ИСПОЛЬЗУЯ ПРАВИЛЬНЫЙ ШЕСТИУГОЛЬНИК ПОСТРОИТЬ
ПРАВИЛЬНЫЙ ТРЕУГОЛЬНИК?
1. Построим правильный
шестиугольник.
А5
2. Соединим точки через
одну: А1, А3, А5.
А4
А6
А3
3. А1А3А5 – искомый
правильный треугольник.
А1
А2

20.

ЗАДАЧА.
КАК, ИСПОЛЬЗУЯ ПРАВИЛЬНЫЙ ШЕСТИУГОЛЬНИК ПОСТРОИТЬ
ПРАВИЛЬНЫЙ ДВЕНАДЦАТИУГОЛЬНИК?
1.
2.
Провести высоты треугольников
до пересечения с окружностью.
Разделить дуги пополам точками
В1, В2, В3, В4, В5, В6.
А5
В4
А4
В5
В3
А6
А3
А1В1А2В2А3В3А4В4А5В5А6В6 –
искомый
двенадцатиугольник.
В6
В2
А1
А2
В1

21.

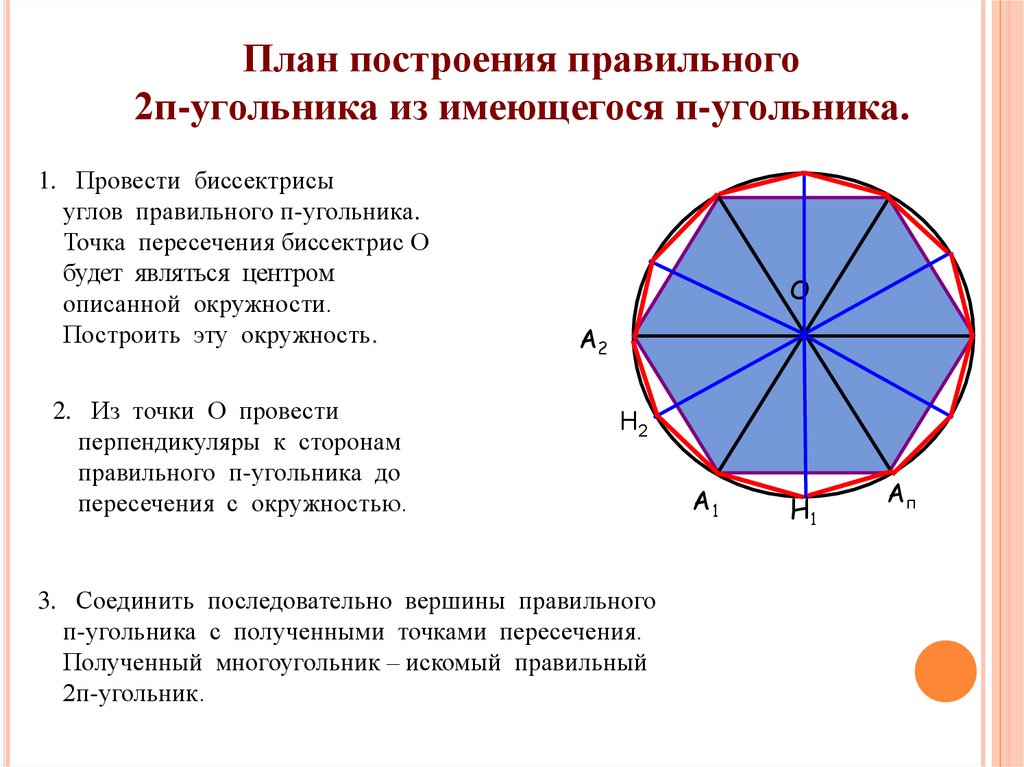
План построения правильного
2п-угольника из имеющегося п-угольника.
1. Провести биссектрисы
углов правильного п-угольника.
Точка пересечения биссектрис О
будет являться центром
описанной окружности.
Построить эту окружность.
2. Из точки О провести
перпендикуляры к сторонам
правильного п-угольника до
пересечения с окружностью.
О
А2
Н2
3. Соединить последовательно вершины правильного
п-угольника с полученными точками пересечения.
Полученный многоугольник – искомый правильный
2п-угольник.
А1
Н1
Ап

22.

Домашнее задание
1.
Радиус окружности, описанной около квадрата,
равен 4√3 см. Найдите сторону квадрата и радиус
вписанной в него окружности.
2. Радиус окружности, вписанной в правильный
шестиугольник, равен 4√3 см. Найдите сторону
шестиугольника и радиус описанной около него
окружности.
3.
Найдите углы правильного n- угольника, если:
а) n=3; б) n=5; в) n=10; г) n=18.
4.
Сколько сторон имеет правильный многоугольник,
если каждый его угол равен: а)60о; б) 135о; в) 150о.

23.

24.

25.

Радиус окружности, описанной около
правильного шестиугольника, равен 5 √3
см. Найдите сторону шестиугольника,
радиус окружности, вписанной в
шестиугольник и его площадь.