Similar presentations:
Правильные многоугольники
1. Правильные многоугольники
Узнать, какой многоугольник называетсяправильным?
Каковы элементы правильного
многоугольника, можно ли их вычислить?
Какими свойствами обладает правильный
многоугольник?
Научиться применять полученные знания к
решению задач
2. Вопросы
По какой формуле вычисляется сумма угловвыпуклого многоугольника?
1. Все углы выпуклого
пятиугольника
равны друг другу.
Найдите величину
каждого угла.
(n 2) 180
0
Решение:
n=5, следовательно
сумма углов =5400
Так как все углы
равны, то
α5 =5400 :5=1080
3.
Что называется серединнымперпендикуляром к отрезку? Каким свойством
обладает каждая его точка?
В
А
Р
О
С
А
Какая окружность называется описанной
около треугольника?
В
4.
Что называется биссектрисой угла? Какимсвойством обладает каждая точка биссектрисы
угла?
•Какая окружность
называется
вписанной в
треугольник?
О
А
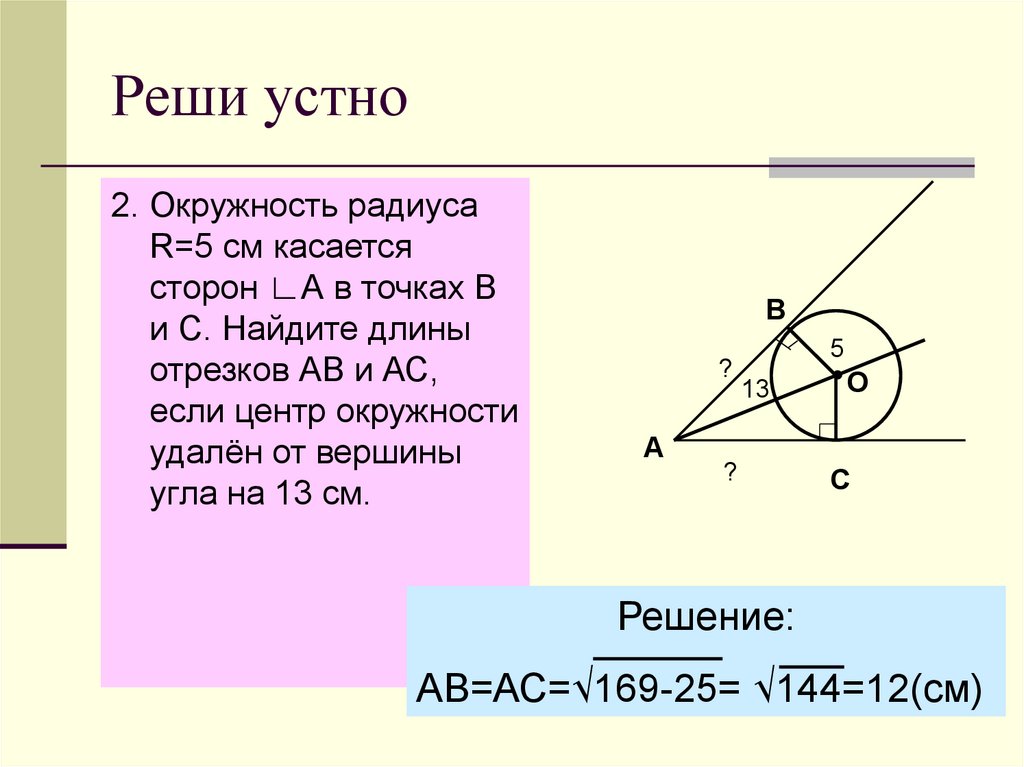
5. Реши устно
2. Окружность радиусаR=5 см касается
сторон ∟А в точках В
и С. Найдите длины
отрезков АВ и АС,
если центр окружности
удалён от вершины
угла на 13 см.
В
?
А
5
13
?
О
С
Решение:
АВ=АС=√169-25= √144=12(см)
6. Правильным многоугольником называется:
1) выпуклый многоугольник,2) у которого все углы равны,
3) все стороны равны.
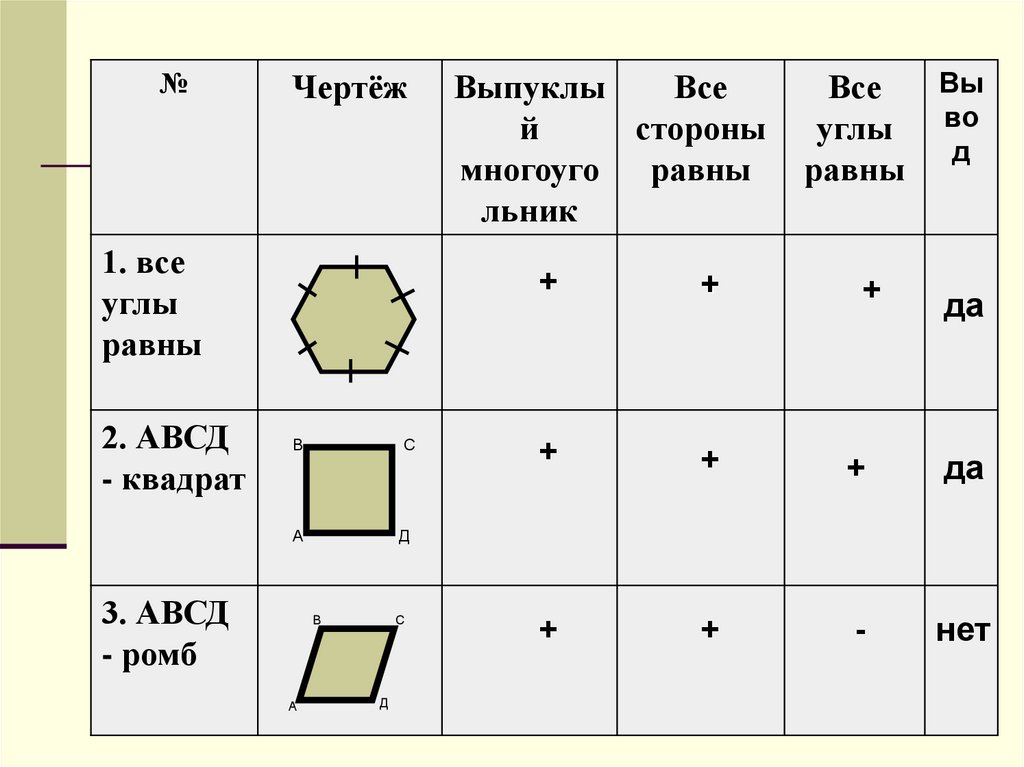
7.
№Чертёж
1. все
углы
равны
2. АВСД
- квадрат
В
С
А
3. АВСД
- ромб
Вы
Все
углы во
д
равны
+
+
+
+
+
да
+
+
-
нет
+
да
Д
В
А
Выпуклы
Все
й
стороны
многоуго равны
льник
С
Д
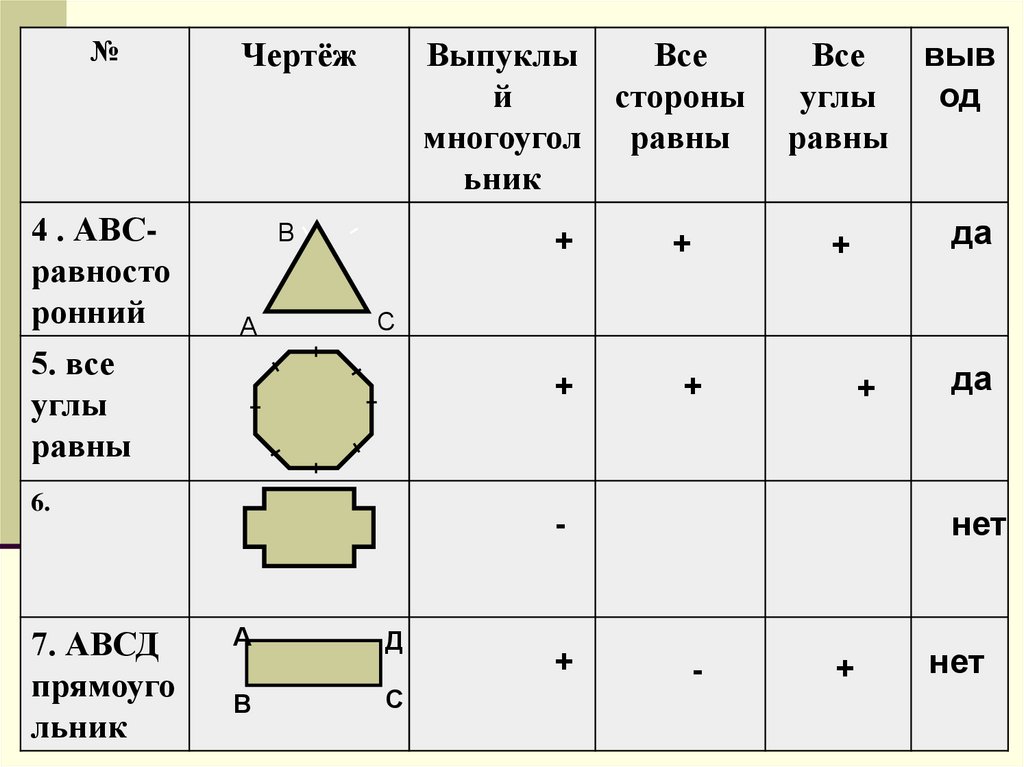
8.
№4 . АВСравносто
ронний
5. все
углы
равны
Чертёж
Выпуклы
Все
й
стороны
многоугол равны
ьник
В
А
+
+
В
да
+
+
+
Д
С
+
да
нет
А
выв
од
С
6.
7. АВСД
прямоуго
льник
+
Все
углы
равны
-
+
нет
9.
Правильные n- угольникиВ
А
С
В
А
С
Д
10. Формула для вычисления угла αn правильного n-угольника
А1Дано: правильный n -угольник
Найти: αn
А2
А6
А3
Решение:
Сумма всех углов
многоугольника равна:
А4
А5
(n 2) 180
Так как все углы правильного
многоугольника равны, то
получим:
0
(n 2)
0
n
180
n
11.
Образец оформления № 1081 г)Дано: правильный n-угольник
n=10
Найти: α10 =?
Решение:
(n 2)
0
n
180
n
(10 2)
0
0
0
10
180 8 18 144
10
12. Решение задач
№1083 (в)Дано: αn= 1350
Найти: n-?
Решение:
(n 2)
0
n
180
n
n 2
0
135
180
n
0
0
0
135 n 180 n 360
0
180 n 135 n 360
0
0
45 n 360
0
n 8
Ответ: многоугольник имеет 8 сторон.
0
0
13. Теорема: Около любого правильного многоугольника можно описать окружность, и притом только одну.
Дано:А1А2А3…Аn-правильный многоугольникДоказать: 1) можно описать окружность
2) такая окружность единственная
Вопросы :
1. Когда мы сможем построить окружность?
2. Каким свойством обладает центр
окружности?
3. Какая окружность называется описанной
около многоугольника?
Нужна точка,
равноудаленная от
всех вершин
правильного
п-угольника
14.
А3А4
5
А2
А5
4
3
О
1
А1
2
Аn
15.
Теорема: в любой правильный многоугольникможно вписать окружность, и притом
только одну.
А2
А3
Н2
Н1
Н3
О
А1
Нn
Аn












 mathematics
mathematics








