Правильные многоугольники. 8 класс

1. Правильные многоугольники 8 класс

МБОУ «СОШ №14»
Правильные
многоугольники
8 класс
г.Череповец

2.

Где в жизни вы встречались
с многоугольниками?

3. Задание 1 : Практическое задание (в группах).

Постройте узор из квадратов
и равносторонних
треугольников, таким
образом, чтобы получился
шестиугольник и
двенадцатиугольник.

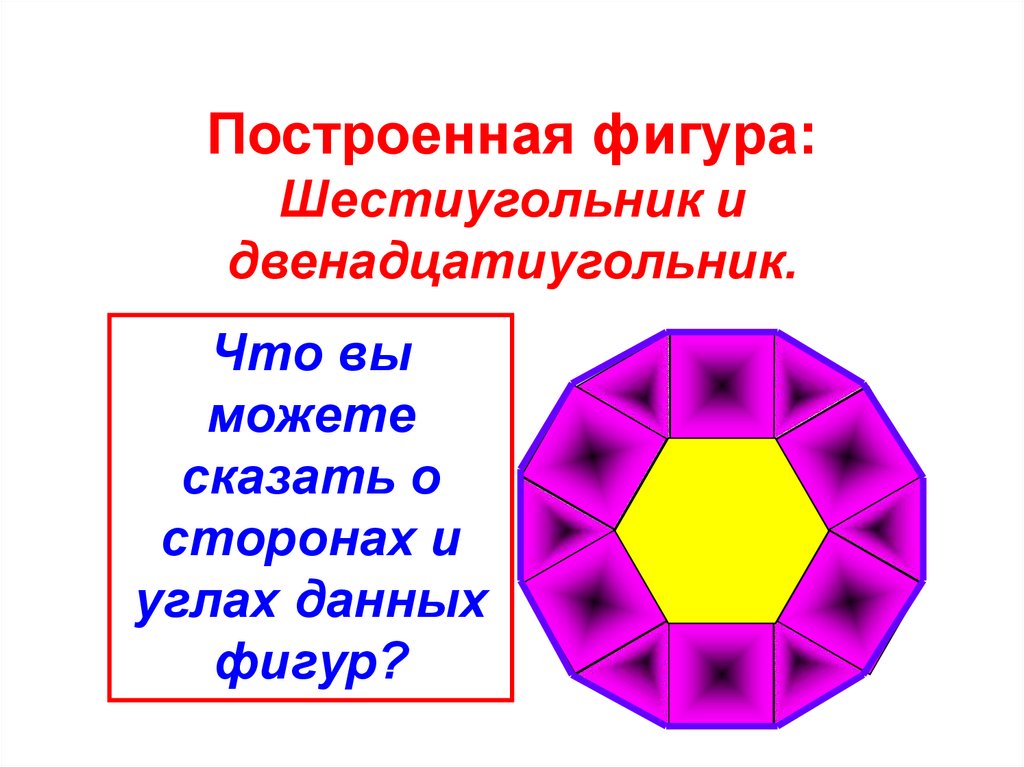
4. Построенная фигура: Шестиугольник и двенадцатиугольник.

Что вы
можете
сказать о
сторонах и
углах данных
фигур?

5.

Выпуклый
многоугольник
называется
правильным, если у
него все углы равны и
все стороны равны

6. Задачи урока:

1) Ввести понятие правильного
многоугольника.
2) Вывести формулу для
вычисления угла правильного nугольника и показать ее
применение в процессе решения
задач.

7. Задание 2 : БИНАРНЫЙ ТЕСТ2 (индивидуально).

1.
2.
3.
4.
5.
6.
7.
Любой правильный многоугольник
является выпуклым.
Любой выпуклый многоугольник
является правильным.
Многоугольник является правильным,
если он выпуклый и все его стороны
равны.
Многоугольник является правильным,
если он выпуклый и все его углы
равны.
Любой четырехугольник с равными
сторонами является правильным.
Любой четырехугольник с равными
углами является правильным.
Любой правильный четырехугольник
является квадратом
1 ДА
НЕТ
2 ДА
НЕТ
3 ДА
НЕТ
4 ДА
НЕТ
5 ДА
НЕТ
6 ДА
НЕТ
7 ДА
НЕТ

8.

Задание 3 : Работа в группах.
Чему равен каждый из углов
правильного многоугольника:
1 группа
2 группа
3 группа
4 группа
1)
2)
1)
2)
пятиугольника;
n – угольника.
восьмиугольника;
n – угольника.
1)
2)
1)
2)
десятиугольника;
n – угольника.
восемнадцатиугольника;
n – угольника.

9.

Проверка.
1 группа
α5 = 108°
2 группа
α8 = 135 °
3 группа
α10 = 144°
4 группа
α18 = 160°
Вывод:
Формула для вычисления угла правильного
n-угольника
nn 22
0
0
n n
180
180
nn

10. Задание 3 : Работа в группах. Чему равен каждый из углов правильного многоугольника:

Задание 4 :Работа в группах.
В таблице заполните пустые клетки ( n-угол
правильного n-угольника, n-сторон, S n- сумма
углов правильного n-угольника).
Решение задач записать в тетрадь.
№
n
Sn
n
1)
?
?
108°
2)
20
?
?
3)
?
1260°
?

11.

Решение задач.
1) Дано: αn = 108°
Найти: n = ? и Sn = ?
n 2
Решение:
0
n
180
n
1. n · αn = 180°(n -2)
2. Sn = n · αn
108° n = 180°(n -2)
Sn = 108° · 5 = 540°
72° n = 360°
n=5
Ответ: n = 5 и S5= 540°

12. Задание 4 :Работа в группах. В таблице заполните пустые клетки (n-угол правильного n-угольника, n-сторон, S n- сумма углов

Решение задач.
2) Дано: n = 20
Найти: αn = ? и Sn = ?
Решение:
1. Sn = 180°(n -2)
Sn = 180°(20 - 2)
Sn = 3240°
2. αn = Sn : n
α20 = 3240° : 20 = 162°
Ответ: α20 = 162° и S20= 3240°

13. Решение задач.

3) Дано: Sn = 1260°
Найти: αn = ? и n = ?
Решение:
n 2
0
n
180
n
1. 1260°= 180°(n - 2)
1260°= 180°n - 360°
180°n =360°+ 1260°
n=9
Ответ: α9 = 140° и n = 9.
2.αn = 1260° : 9 = 140°

14. Решение задач.

Проверка.
№
n
Sn
n
1)
5
540°
108°
2)
20
3240°
162°
3)
9
1260°
140°

15. Решение задач.

Задание 5: Устная работа.
1. Многоугольник называется
правильным если …….
2. Сумма углов многоугольника
равна…….
3. Прямоугольник……….правильным
многоугольником.
4. Угол правильного многоугольника
равен……………………
5. Квадрат…………………..правильным
многоугольником.
6. Ромб ……………………….правильным
многоугольником.

16. Проверка.

Задание 6: Творческое задание.
Возможно кто-то из вас в будущем
займется этим творческим и
интересным занятием.
Представьте, что к вам в фирму
пришел заказчик. Сколько вариантов
покрытия паркета из правильных
многоугольников вы предложите?
Замечание: Покрывать плоскость
паркетом необходимо без просветов.

17. Задание 5: Устная работа.

Вывод:
Плоскость без просветов можно
покрыть правильными
треугольниками, квадратами и
правильными
шестиугольниками (если
многоугольники одного вида).

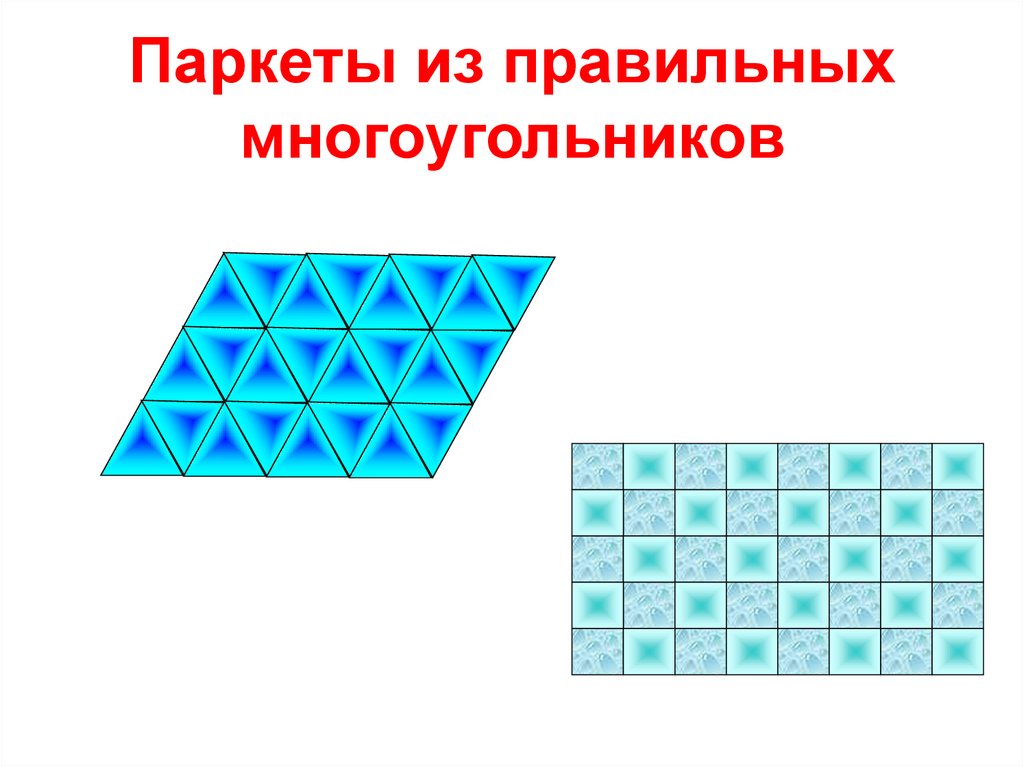
18. Задание 6: Творческое задание.

Паркеты из правильных
многоугольников

19. Вывод:

А если многоугольники
разных видов?

20. Паркеты из правильных многоугольников

Домашнее задание:
1) Составить орнамент, элемент паркета из
правильных многоугольников (различные
виды многоугольников) с помощью
компьютера.
2) Составить задачу и обратные к ней на
применение формулы для вычисления угла
правильного n – угольника.

21.

Дополнительно:
Задача №1082
Чему равна сумма внешних углов
правильного n- угольника, если при
каждой вершине взято по одному
внешнему углу?