Многоугольники

1.

2.

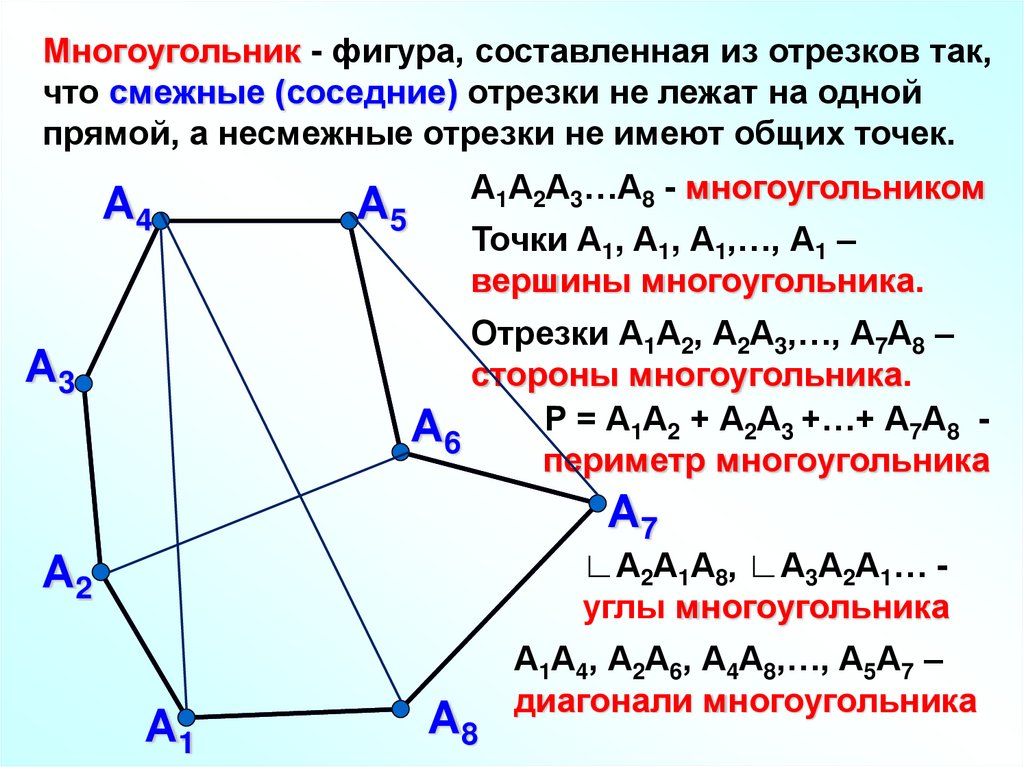
Многоугольник - фигура, составленная из отрезков так,
что смежные (соседние) отрезки не лежат на одной
прямой, а несмежные отрезки не имеют общих точек.
А4
А5
А1А2А3…А8 - многоугольником
Точки А1, А1, А1,…, А1 –
вершины многоугольника.
Отрезки А1А2, А2А3,…, А7А8 –
стороны многоугольника.
Р = А1А2 + А2А3 +…+ А7А8 А6
периметр многоугольника
А3
А7
А2
∟А2А1А8, ∟А3А2А1… углы многоугольника
А1
А8
А1А4, А2А6, А4А8,…, А5А7 –
диагонали многоугольника

3.

Две вершины, принадлежащие одной стороне
называются соседними
Стороны, являющиеся соседними отрезками,
называются соседними сторонами
В
С
D
А
E
G
F

4.

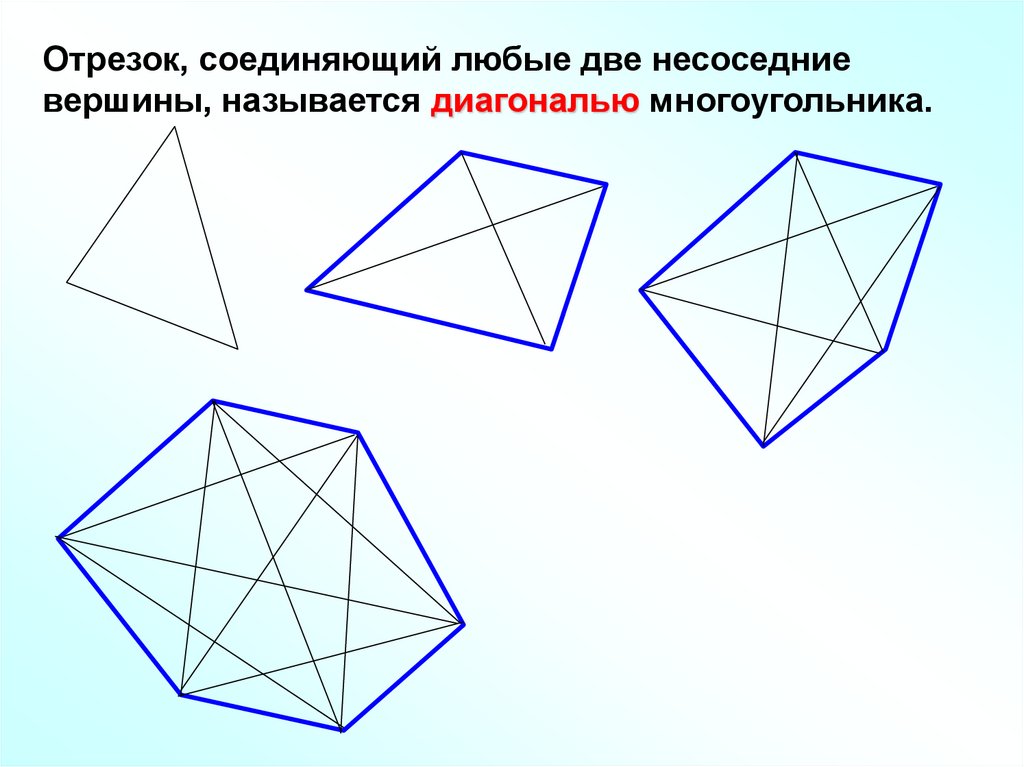
Отрезок, соединяющий любые две несоседние
вершины, называется диагональю многоугольника.

5.

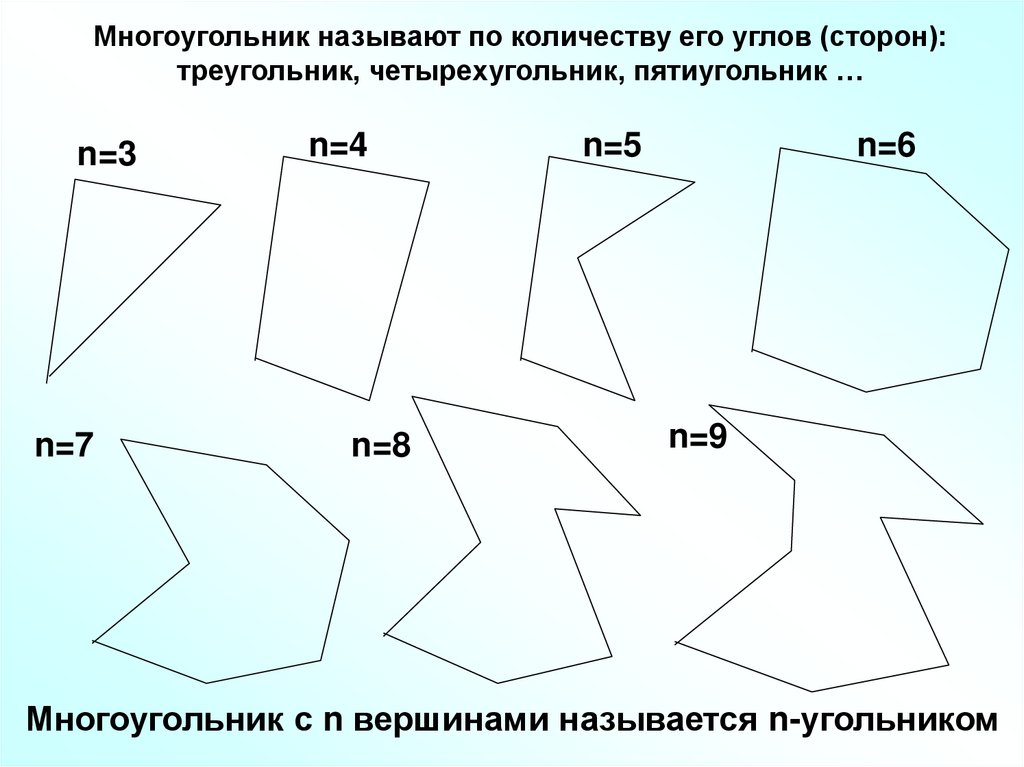
Многоугольник называют по количеству его углов (сторон):
треугольник, четырехугольник, пятиугольник …
n=3
n=7
n=4
n=8
n=5
n=6
n=9
Многоугольник с n вершинами называется n-угольником

6.

Примеры многоугольников

7.

Фигуру, состоящую из многоугольника и его
внутренней области, также называют
многоугольником.
В
А2
С
А1
А3
А
D
А7
E
H
А6
G
F
А5
А4

8.

Выпуклый многоугольник - многоугольник, все углы
которого меньше развернутого.
АВСDЕ – выпуклый многоугольник.
Свойства:
1) Расположен в одной полуплоскости относительно
любой прямой, содержащей его сторону
С
D
В
Е
А
2) Выпуклый многоугольник
(кроме треугольника)
содержит любую свою
диагональ.

9.

Е
D
С
F
В
G
А
Невыпуклый многоугольник многоугольник, части которого
расположены в разных
полуплоскостях относительно
любой прямой, содержащей его
сторону.
АВСDEFG – невыпуклый
многоугольник.

10.

Среди диагоналей невыпуклого многоугольника
найдутся такие, которые лежат во внешней
области.

11.

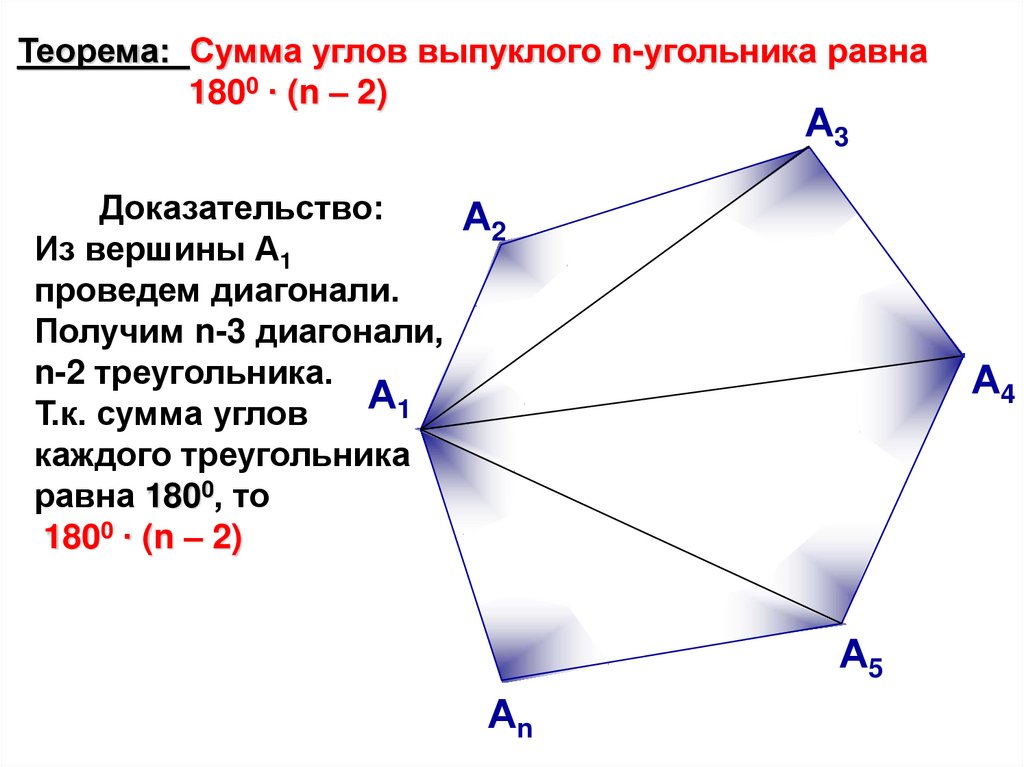
Теорема: Сумма углов выпуклого n-угольника равна
1800 ∙ (n – 2)
А3
Доказательство:
А2
Из вершины А1
проведем диагонали.
Получим n-3 диагонали,
n-2 треугольника.
А1
Т.к. сумма углов
каждого треугольника
равна 1800, то
1800 ∙ (n – 2)
А4
А5
Аn

12.

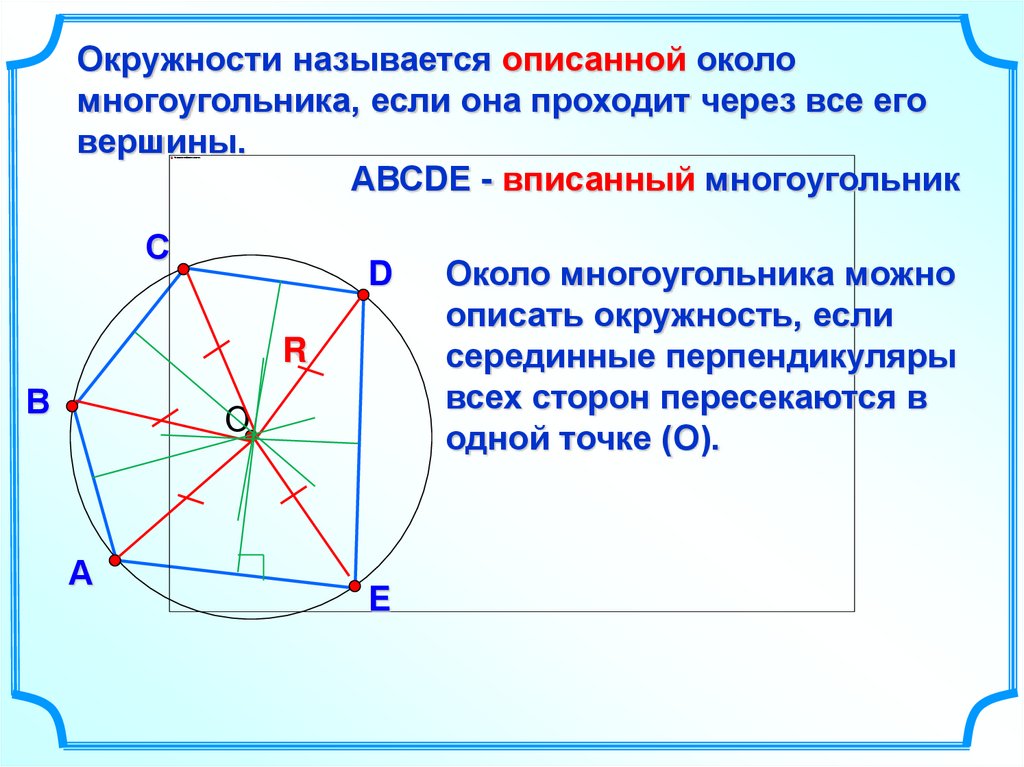
Окружности называется описанной около
многоугольника, если она проходит через все его
вершины.
АВСDЕ - вписанный многоугольник
С
D
R
В
О
А
E
Около многоугольника можно
описать окружность, если
серединные перпендикуляры
всех сторон пересекаются в
одной точке (О).

13.

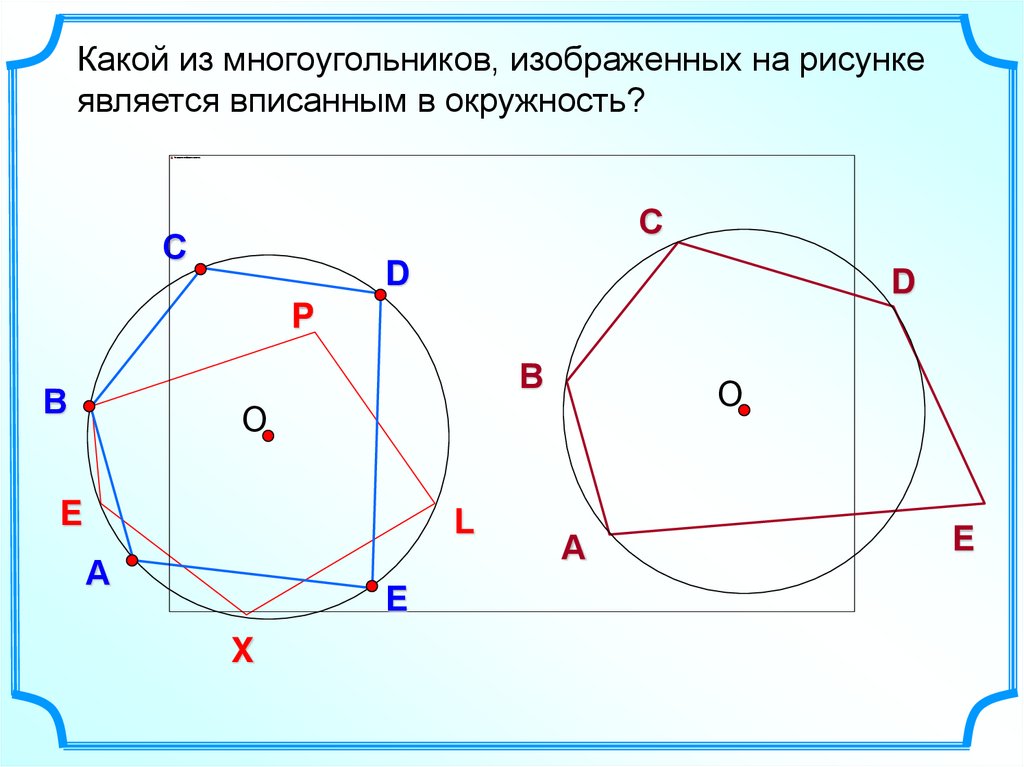
Какой из многоугольников, изображенных на рисунке
является вписанным в окружность?
С
С
D
D
P
В
В
О
О
E
L
А
E
X
А
E

14.

Какой из двух четырехугольников АВСD или АЕКD
является описанным?
К
С
E
В
О
D
А

15.

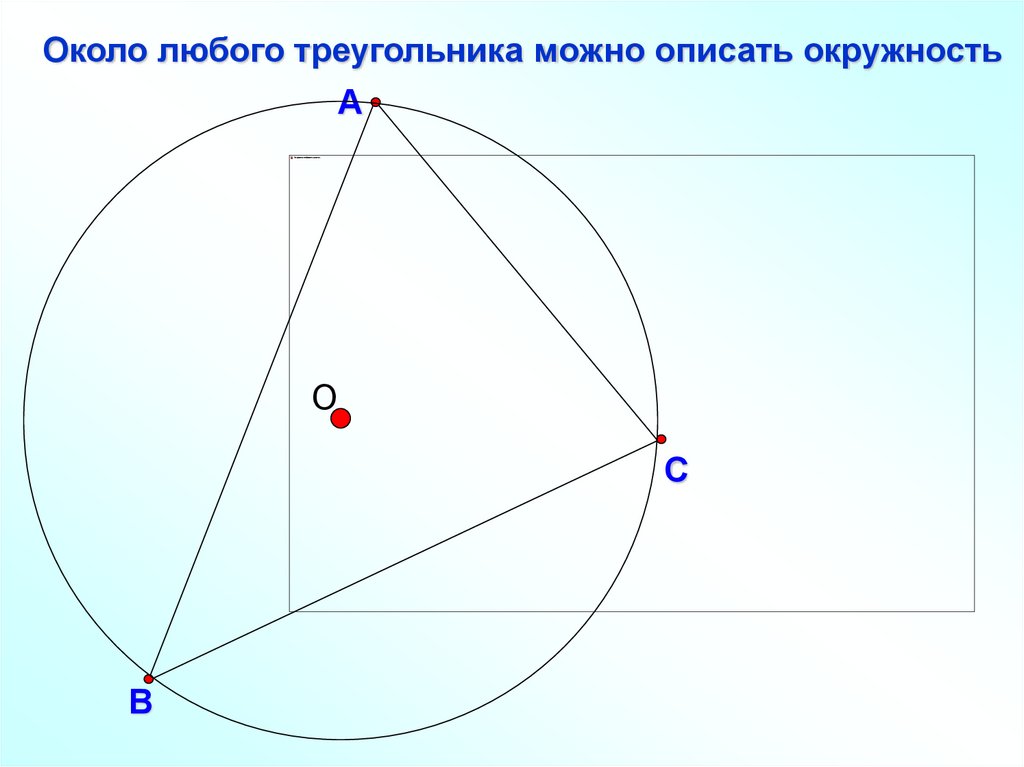
Около любого треугольника можно описать окружность
А
О
С
В

16.

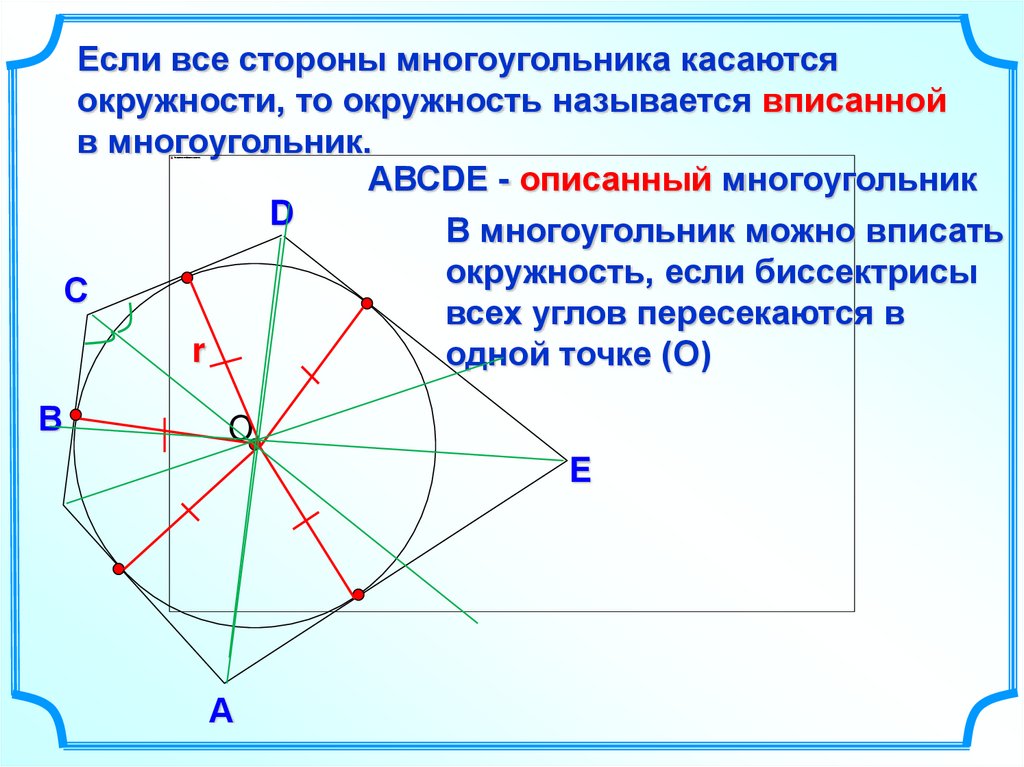
Если все стороны многоугольника касаются
окружности, то окружность называется вписанной
в многоугольник.
АВСDЕ - описанный многоугольник
D
В многоугольник можно вписать
окружность, если биссектрисы
всех углов пересекаются в
одной точке (О)
С
r
В
О
E
А

17.

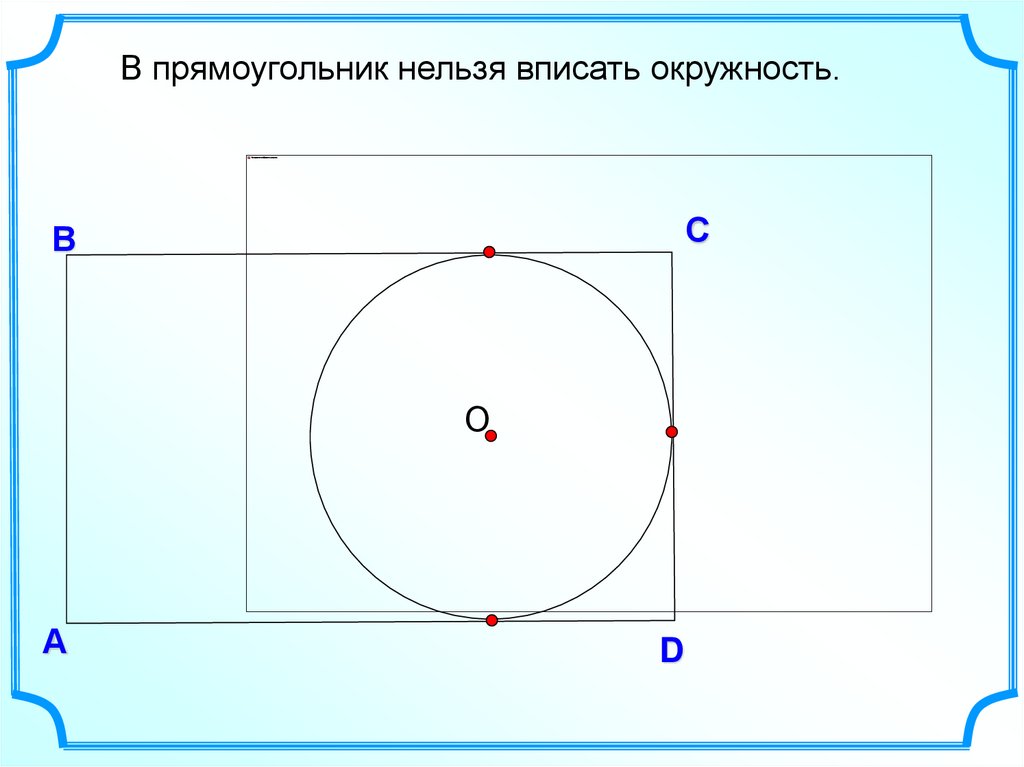
В прямоугольник нельзя вписать окружность.
С
В
О
А
D

18.

В любой треугольник можно вписать окружность.
А
О
С
В

19.

Тренировочные задания на готовых чертежах.
Все углы выпуклого восьмиугольника равны между
собой. Чему равна градусная мера каждого из углов
восьмиугольника?

20.

В выпуклом
десятиугольнике
соединили
отрезками
середины
каждых двух
соседних сторон.
Найти сумму
углов
образовавшегося
многоугольника.

21.

Величины углов выпуклого шестиугольника
пропорциональны числам 1; 2; 3; 4; 4; 4. Найдите
величину меньшего из углов этого шестиугольника.
4х
4х
4х
х
2х
3х

22.

n-угольник
Прямая,
проходящая
через
середины
двух
соседних
сторон
выпуклого
33-угольника,
разбивает
его на
треугольник
и n-угольник.
n-?

23.

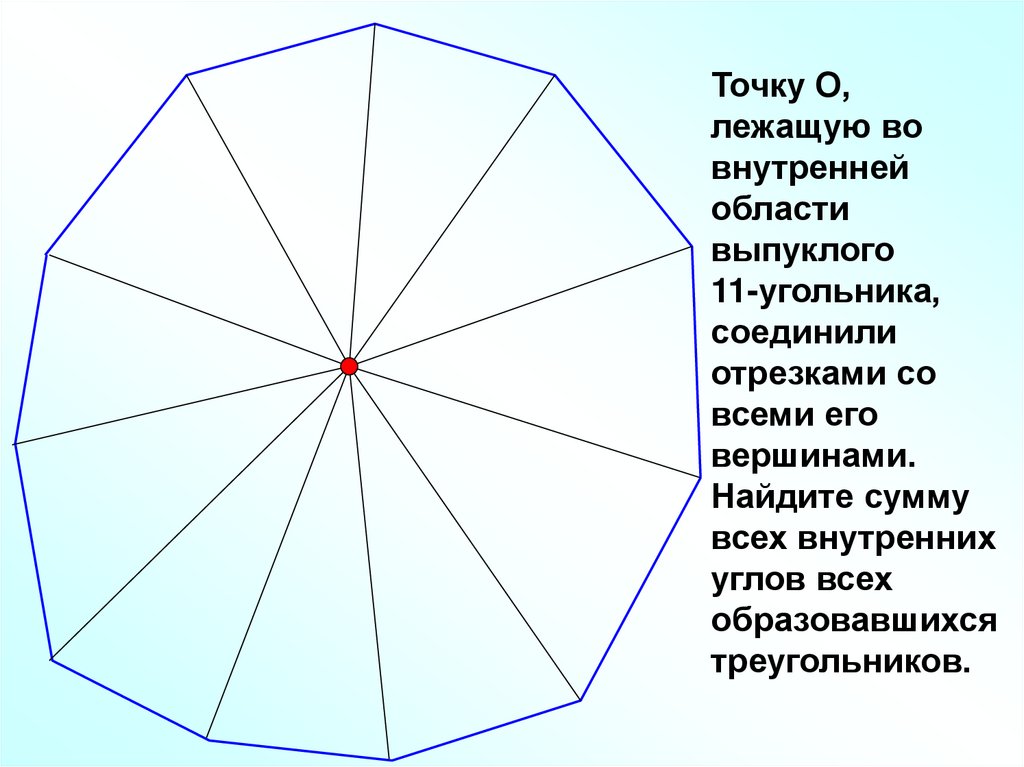
Точку О,
лежащую во
внутренней
области
выпуклого
11-угольника,
соединили
отрезками со
всеми его
вершинами.
Найдите сумму
всех внутренних
углов всех
образовавшихся
треугольников.

24.

2
180 2
3
1
180 1
180 3
4
180 4
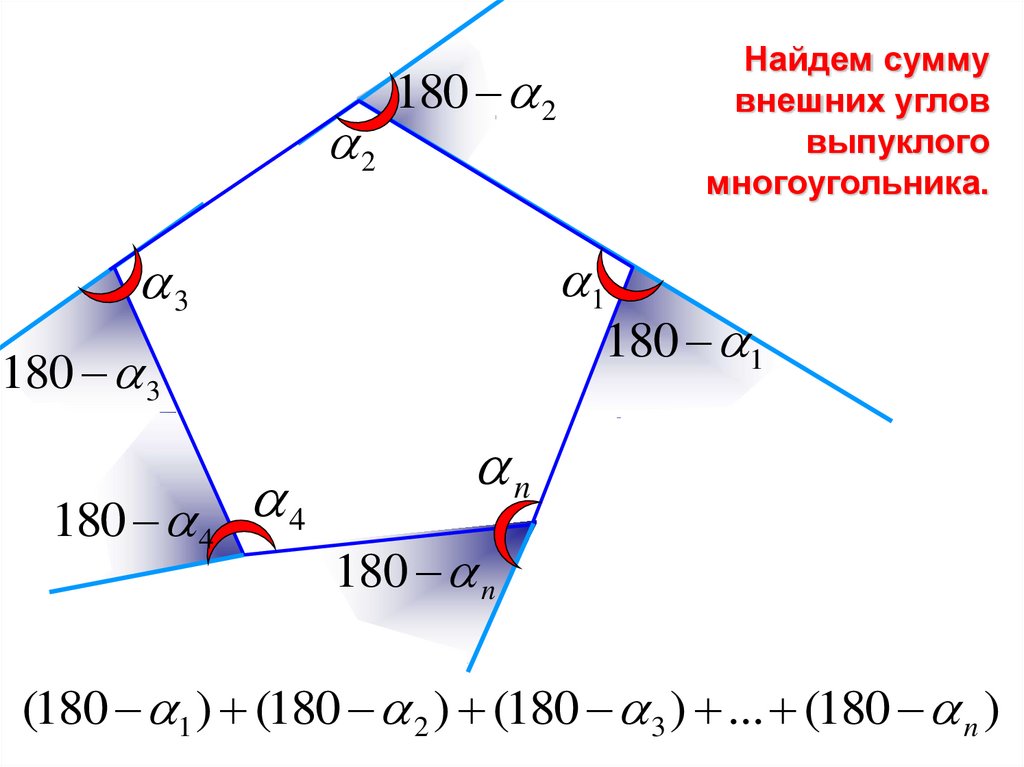
Найдем сумму
внешних углов
выпуклого
многоугольника.
n
180 n
(180 1 ) (180 2 ) (180 3 ) ... (180 n )

25.

Выполним упрощение выражения
n
(180 1 ) (180 2 ) (180 3 ) ... (180 n )
n
180 180 ... 180 ( 1 2 3 ... n )
180n 180(n 2)
180n 180n 360 = 3600
Сумма внешних
углов выпуклого
многоугольника.