Многоугольники. Примеры многоугольников

1.

2.

3.

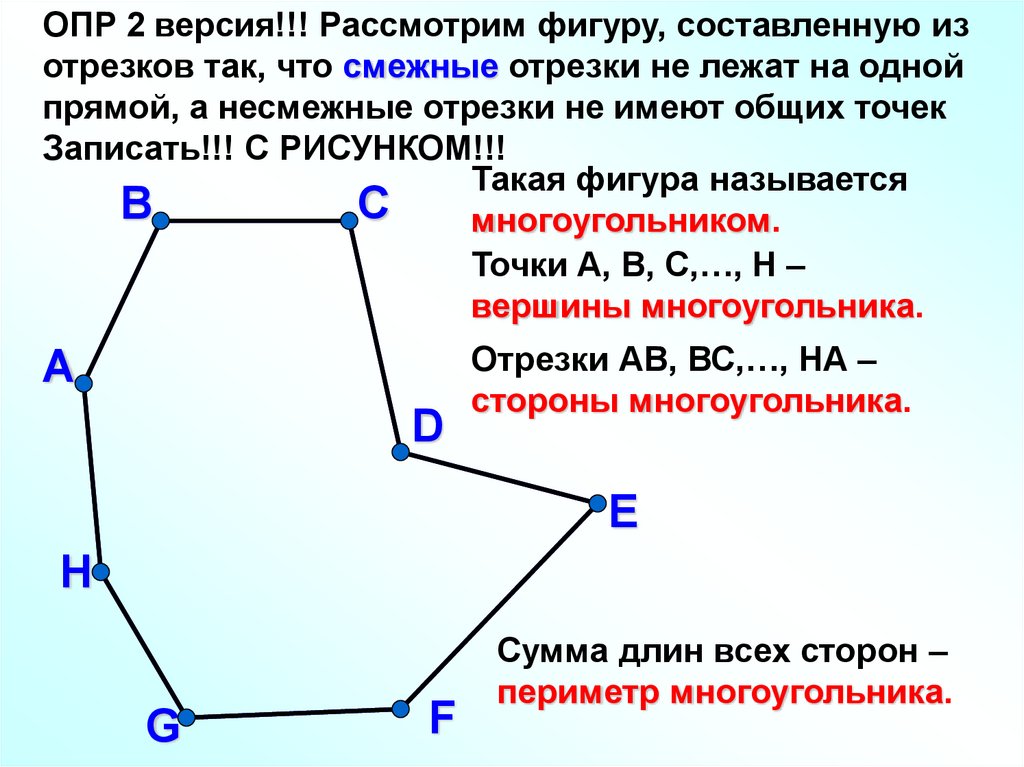
ОПР 2 версия!!! Рассмотрим фигуру, составленную из
отрезков так, что смежные отрезки не лежат на одной
прямой, а несмежные отрезки не имеют общих точек
Записать!!! С РИСУНКОМ!!!
Такая фигура называется
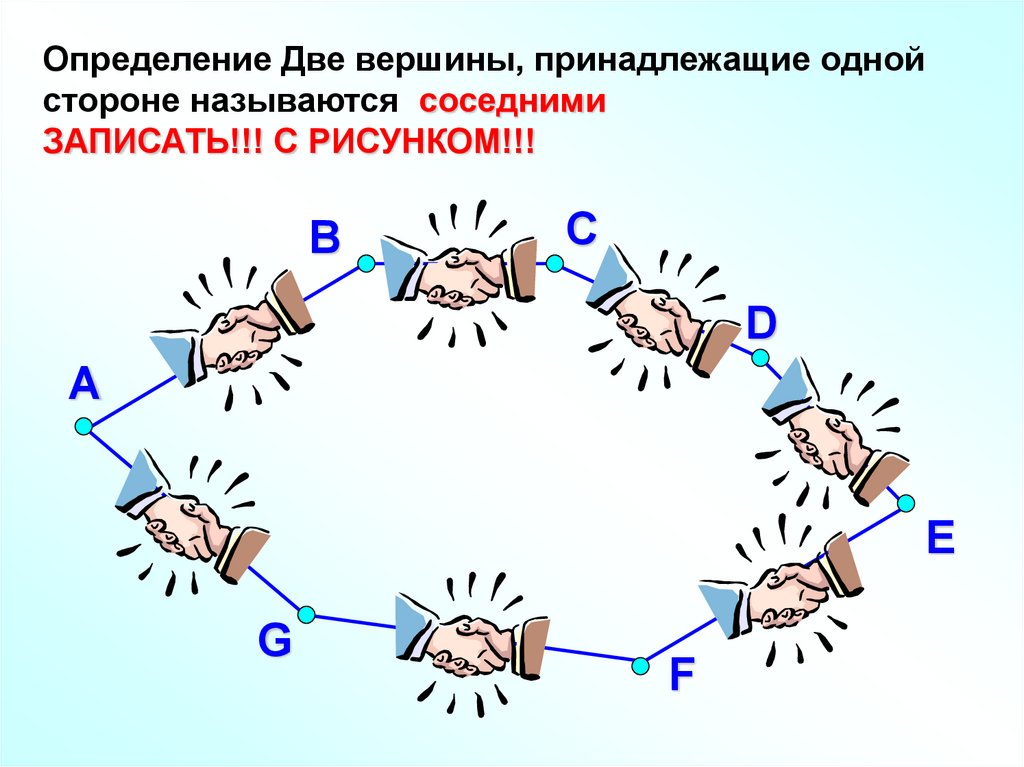
В
С
многоугольником.
Точки А, В, С,…, H –
вершины многоугольника.
А
D
Отрезки АВ, ВС,…, HА –
стороны многоугольника.
E
H
G
F
Сумма длин всех сторон –
периметр многоугольника.

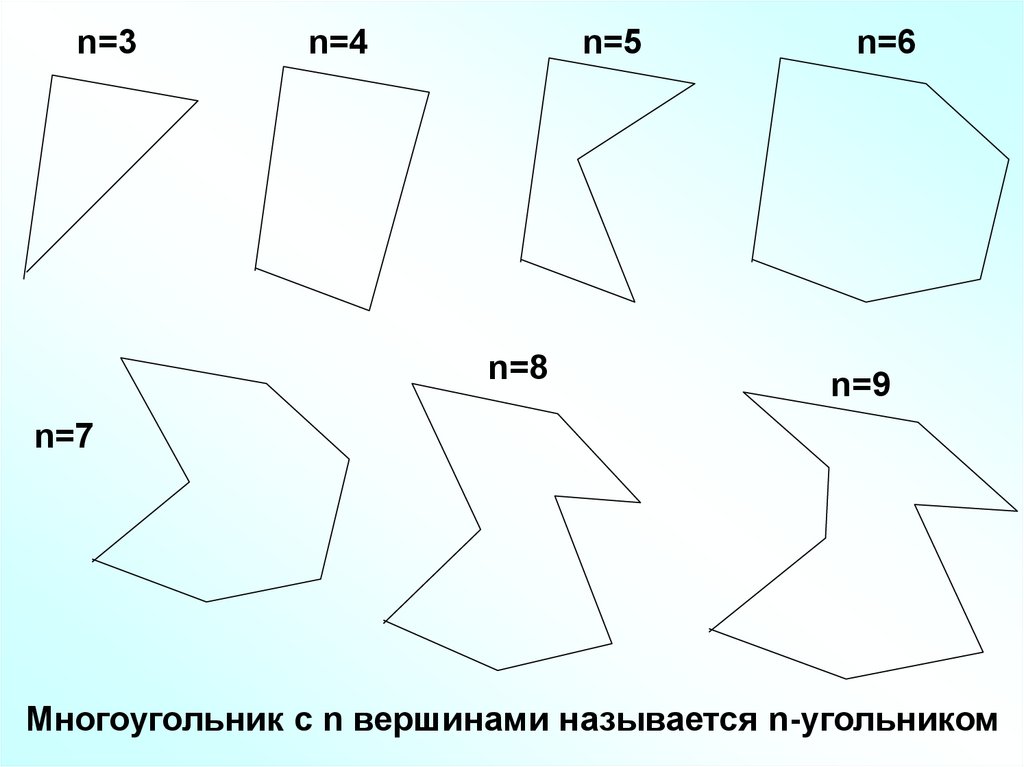
4.

n=3
n=4
n=5
n=8
n=6
n=9
n=7
Многоугольник с n вершинами называется n-угольником

5.

В
С
Любой многоугольник
разделяет плоскость на две
части,
А
D
одна часть называется
внутренней областью,
E
H
G
F
другая часть называется
внешней областью внешней
областью

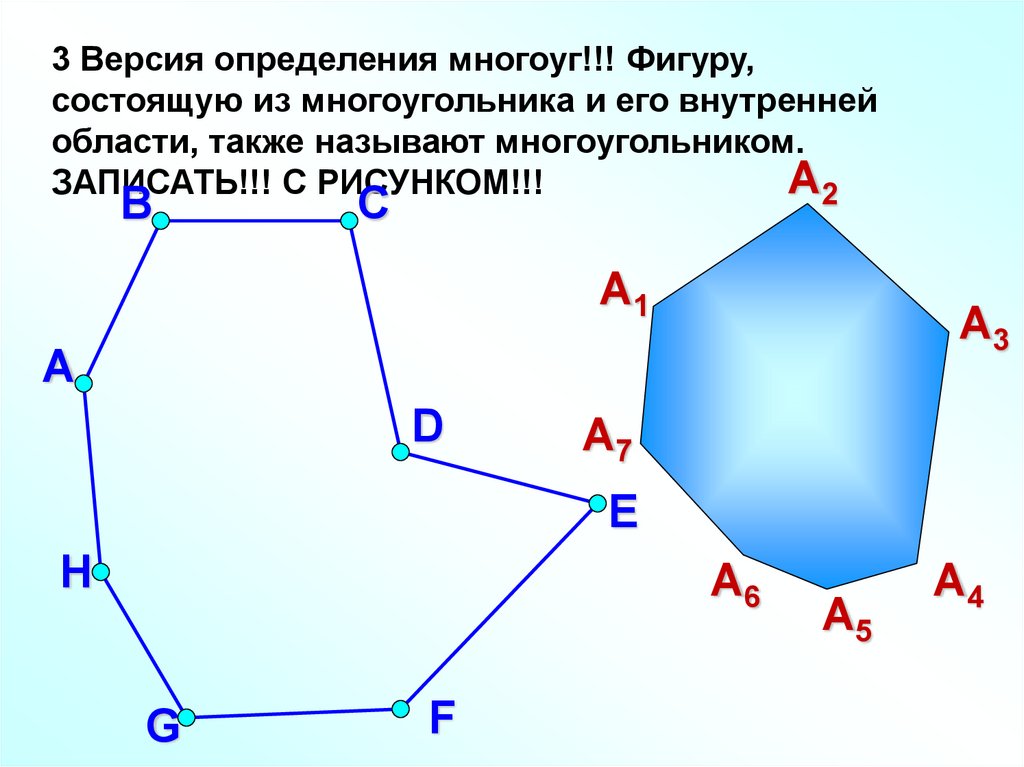
6.

3 Версия определения многоуг!!! Фигуру,
состоящую из многоугольника и его внутренней
области, также называют многоугольником.
А2
ЗАПИСАТЬ!!! С РИСУНКОМ!!!
В
С
А1
А3
А
D
А7
E
H
А6
G
F
А5
А4

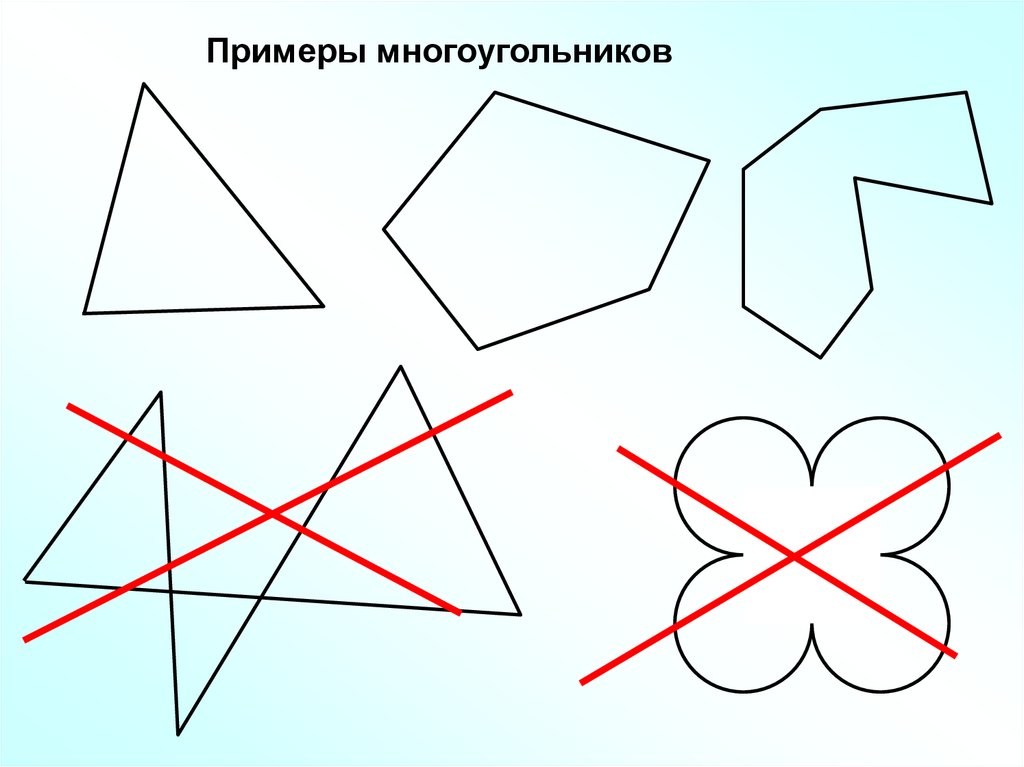
7.

Примеры многоугольников

8.

Определение Две вершины, принадлежащие одной
стороне называются соседними
ЗАПИСАТЬ!!! С РИСУНКОМ!!!
В
С
D
А
E
G
F

9.

Опред Отрезок, соединяющий любые две
несоседние вершины, называется диагональю
многоугольника. ЗАПИСАТЬ с РИСУНКОМ!!!
2
9
5

10.

Отрезок, соединяющий любые две несоседние
вершины, называется диагональю многоугольника.
В
14
С
D
А
E
G
F

11.

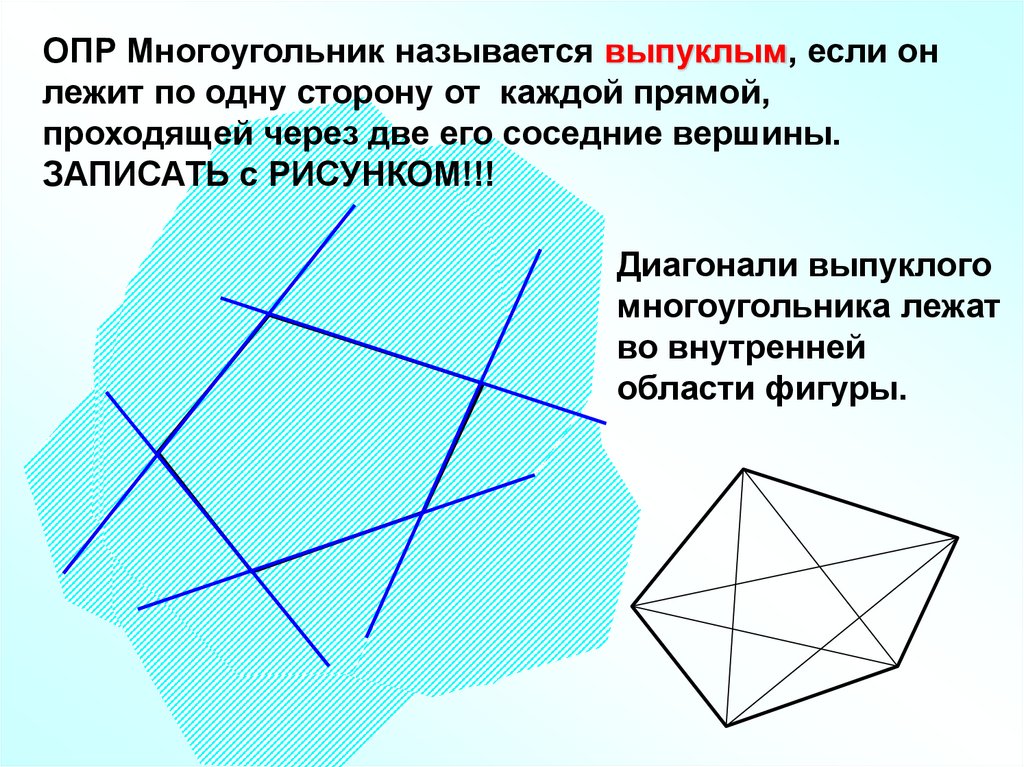
ОПР Многоугольник называется выпуклым, если он
лежит по одну сторону от каждой прямой,
проходящей через две его соседние вершины.
ЗАПИСАТЬ с РИСУНКОМ!!!
Диагонали выпуклого
многоугольника лежат
во внутренней
области фигуры.

12.

Невыпуклый
многоугольник
Среди диагоналей
невыпуклого
многоугольника
найдутся такие,
которые лежат во
внешней области.

13.

ТЕОРЕМА1 Найдем сумму внутренних углов выпуклого nугольника. ЗАПИСАТЬ и ВЫУЧИТЬ!!!
Из вершины А1 построим
А3
диагонали.
А2
Получили
n-3 диагонали,
n-2 треугольника.
А4
А1
(n-2) 1800
А5
Аn

14.

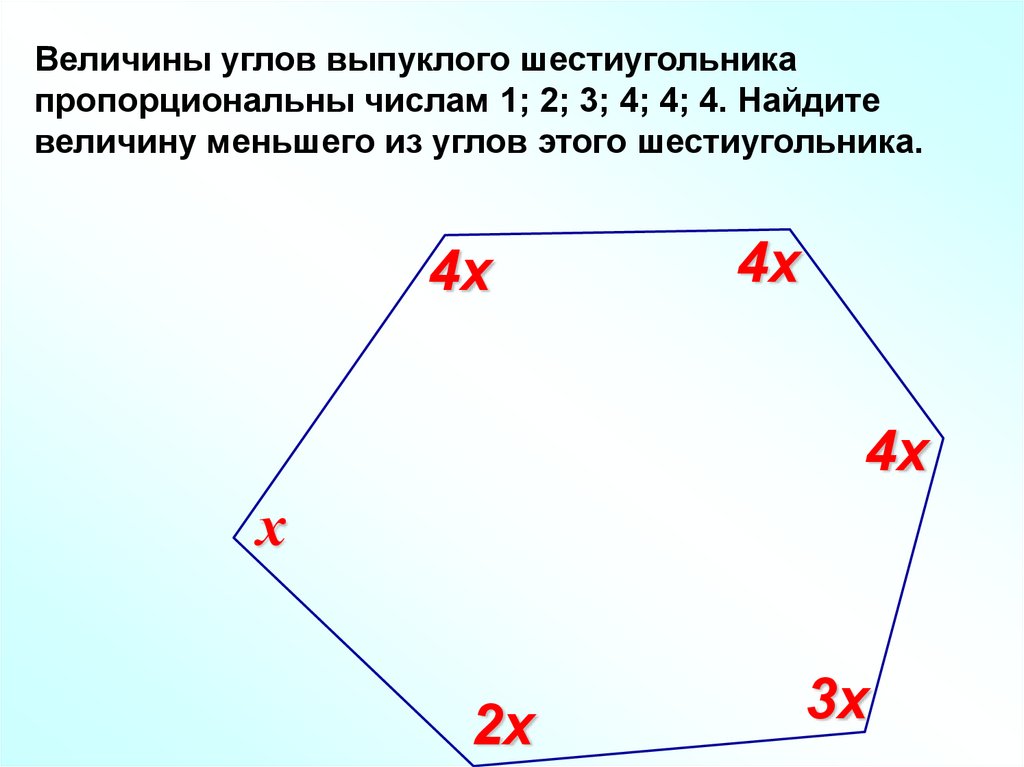
Величины углов выпуклого шестиугольника
пропорциональны числам 1; 2; 3; 4; 4; 4. Найдите
величину меньшего из углов этого шестиугольника.
4х
4х
4х
х
2х
3х

15.

2
180 2
3
1
180 1
180 3
4
180 4
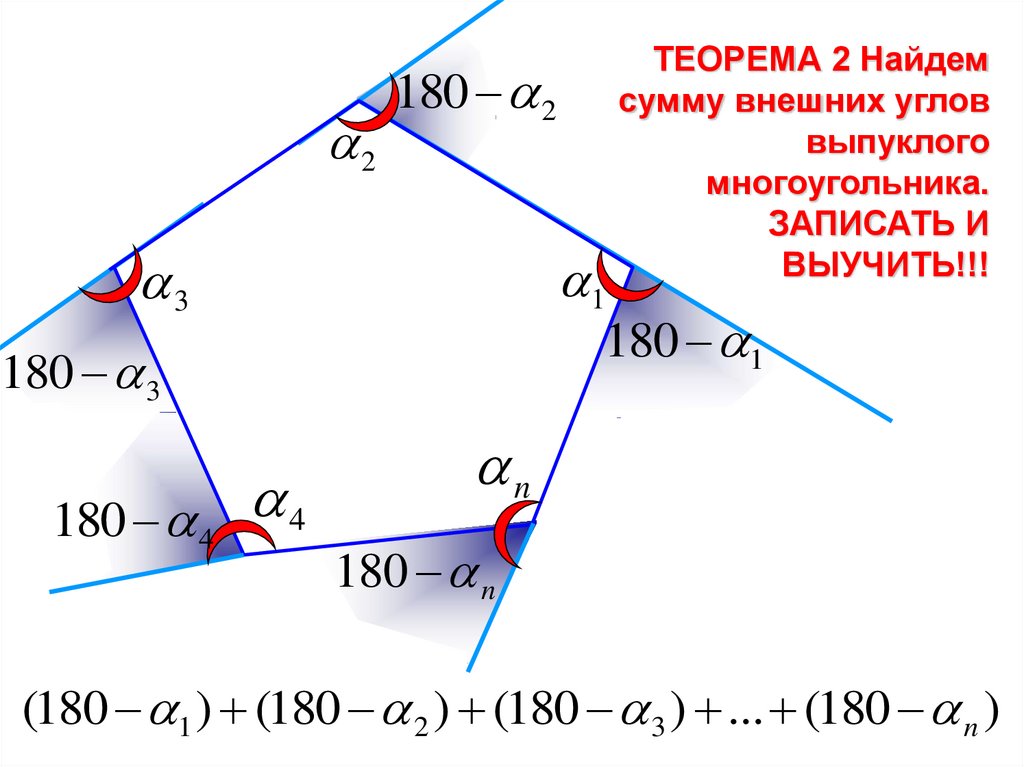
ТЕОРЕМА 2 Найдем
сумму внешних углов
выпуклого
многоугольника.
ЗАПИСАТЬ И
ВЫУЧИТЬ!!!
n
180 n
(180 1 ) (180 2 ) (180 3 ) ... (180 n )

16.

Выполним упрощение выражения
n
(180 1 ) (180 2 ) (180 3 ) ... (180 n )
n
180 180 ... 180 ( 1 2 3 ... n )
180n 180(n 2)
180n 180n 360 = 3600
Сумма внешних
углов выпуклого
многоугольника.

17.

В
4 стороны
4 вершины
2 диагонали
Две несмежные стороны
называются
противоположными
А
D
Две вершины, не
С являющиеся соседними,
называются также
противоположными

18.

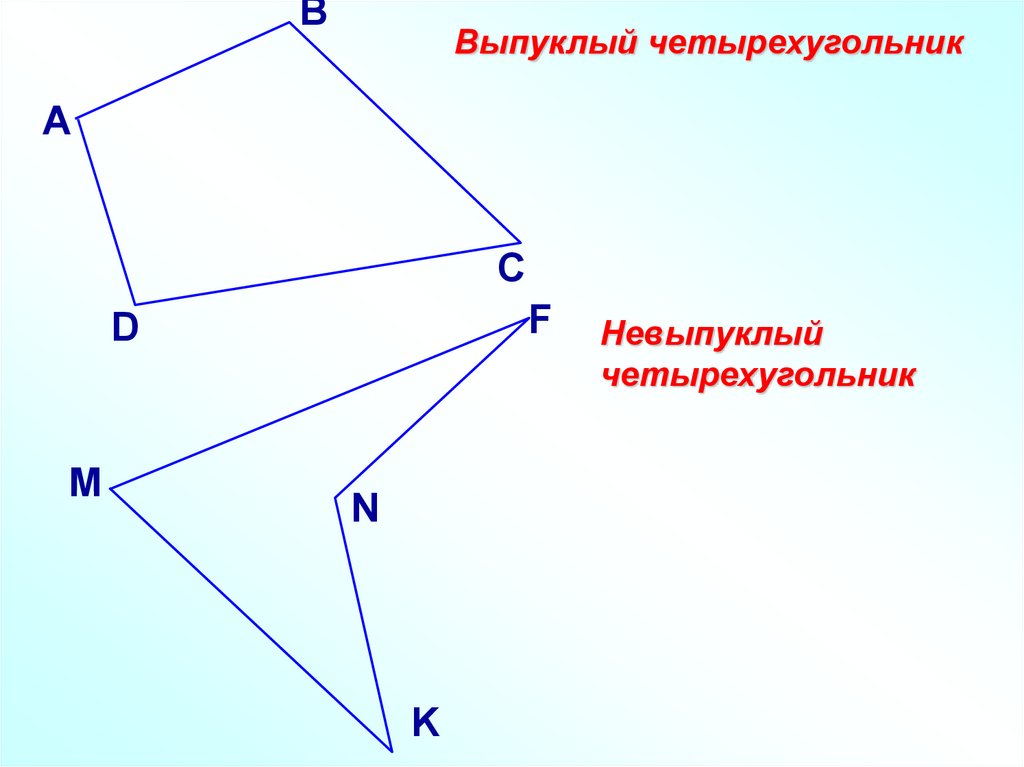
В
Выпуклый четырехугольник
А
С
F
D
M
N
K
Невыпуклый
четырехугольник

19.

В
Выпуклый четырехугольник
Каждая диагональ
выпуклого
четырехугольника
разделяет его на два
С треугольника
А
F
D
M
Невыпуклый
четырехугольник
Одна из диагоналей
невыпуклого
четырехугольника также
разделяет его на два
треугольника.
N
K

20.

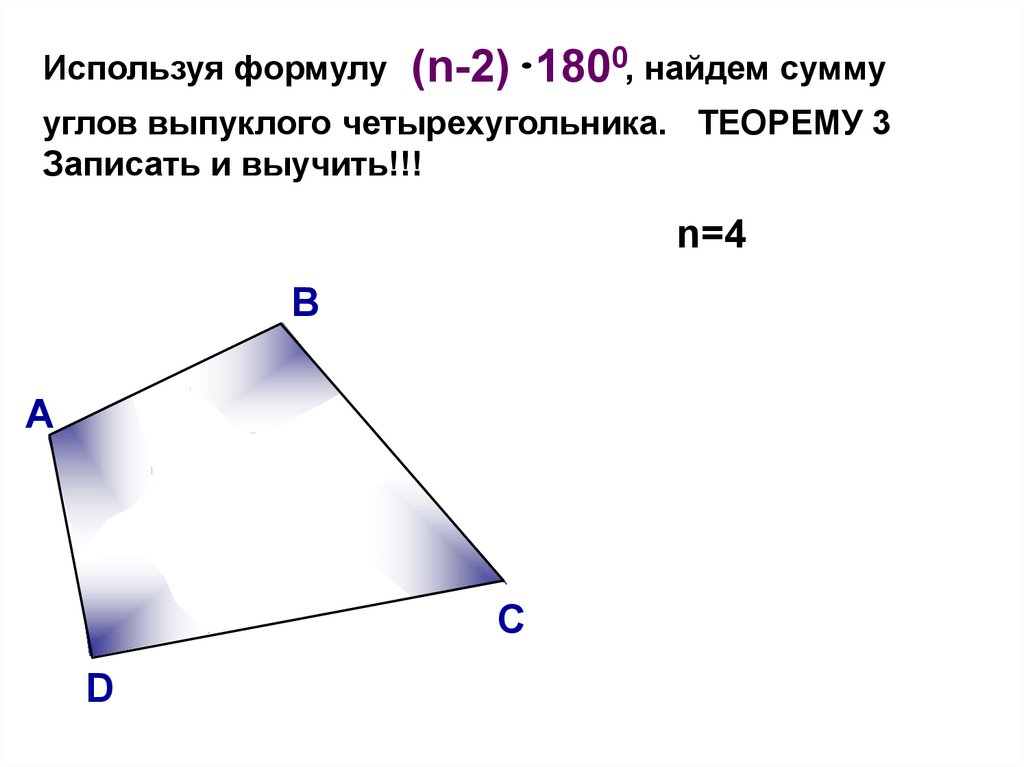
Используя формулу
(n-2) 1800, найдем сумму
углов выпуклого четырехугольника. ТЕОРЕМУ 3
Записать и выучить!!!
n=4
В
А
С
D