Построение правильных многоугольников

1.

Геометрия
Построение
правильных
многоугольников
9класс

2.

3.

В геометрии выделяют задачи на построение,
которые можно решить только с помощью двух
инструментов: циркуля и линейки без масштабных
делений.
Линейка позволяет провести произвольную
прямую, а также построить прямую, проходящую
через две данные точки;
с помощью циркуля можно провести окружность
произвольного радиуса, а также окружность с
центром в данной точке и радиусом, равным
данному отрезку.
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

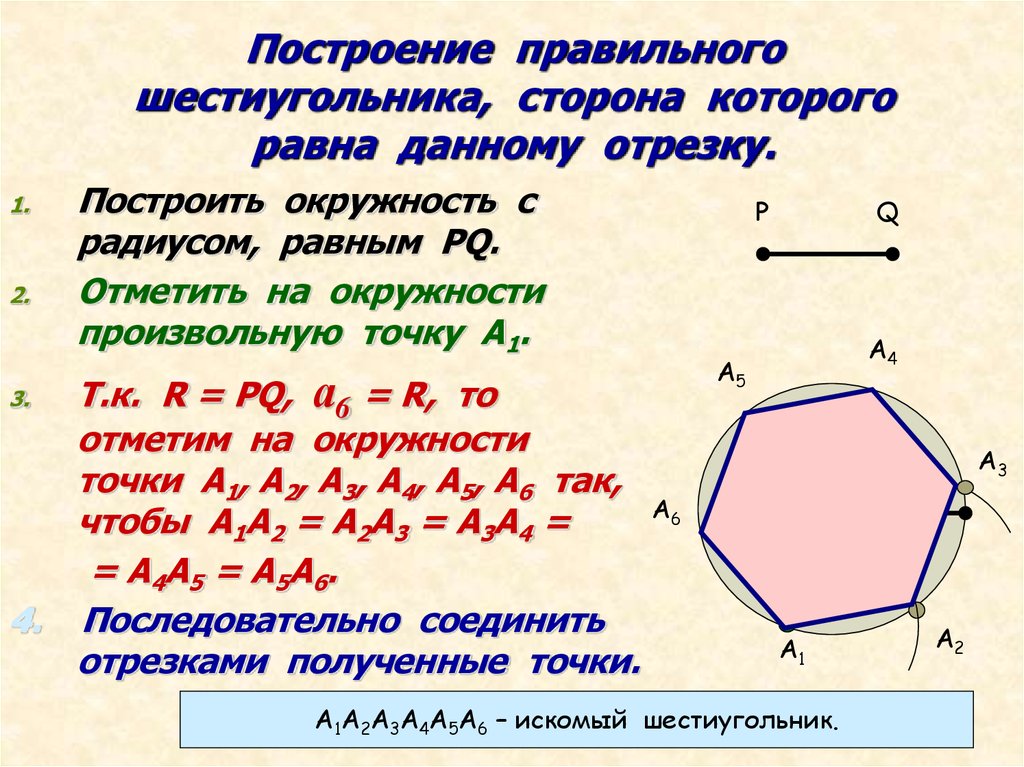
4. Построение правильного шестиугольника, сторона которого равна данному отрезку.

Какая зависимость существует между
стороной правильного шестиугольника и
радиусом описанной около него
окружности?
Ответ: a = R
6
Пусть РQ – заданный отрезок, равный
стороне правильного шестиугольника,
который нам необходимо построить. Чему
равен радиус описанной около этого
шестиугольника
Ответ: PQ. окружности?
Составьте план построения правильного

5. Построение правильного шестиугольника, сторона которого равна данному отрезку.

1.
2.
Построить окружность с
радиусом, равным PQ.
Отметить на окружности
произвольную точку А1.
Т.к. R = PQ, а6 = R, то
отметим на окружности
точки А1, А2, А3, А4, А5, А6 так,
чтобы А1А2 = А2А3 = А3А4 =
= А4А5 = А5А6.
4. Последовательно соединить
отрезками полученные точки.
P
Q
А4
А5
3.
А3
А6
А1
А1А2А3А4А5А6 – искомый шестиугольник.
А2

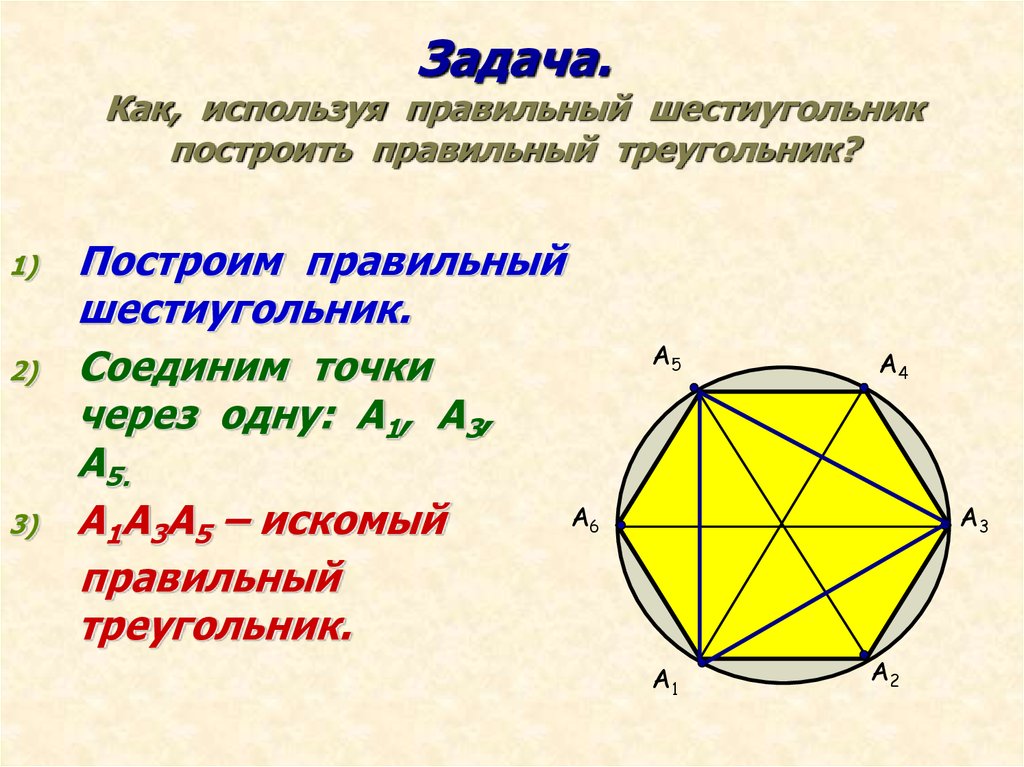
6. Задача. Как, используя правильный шестиугольник построить правильный треугольник?

1)
2)
3)
Построим правильный
шестиугольник.
Соединим точки
через одну: А1, А3,
А5.
А6
А1А3А5 – искомый
правильный
треугольник.
А5
А4
А3
А1
А2

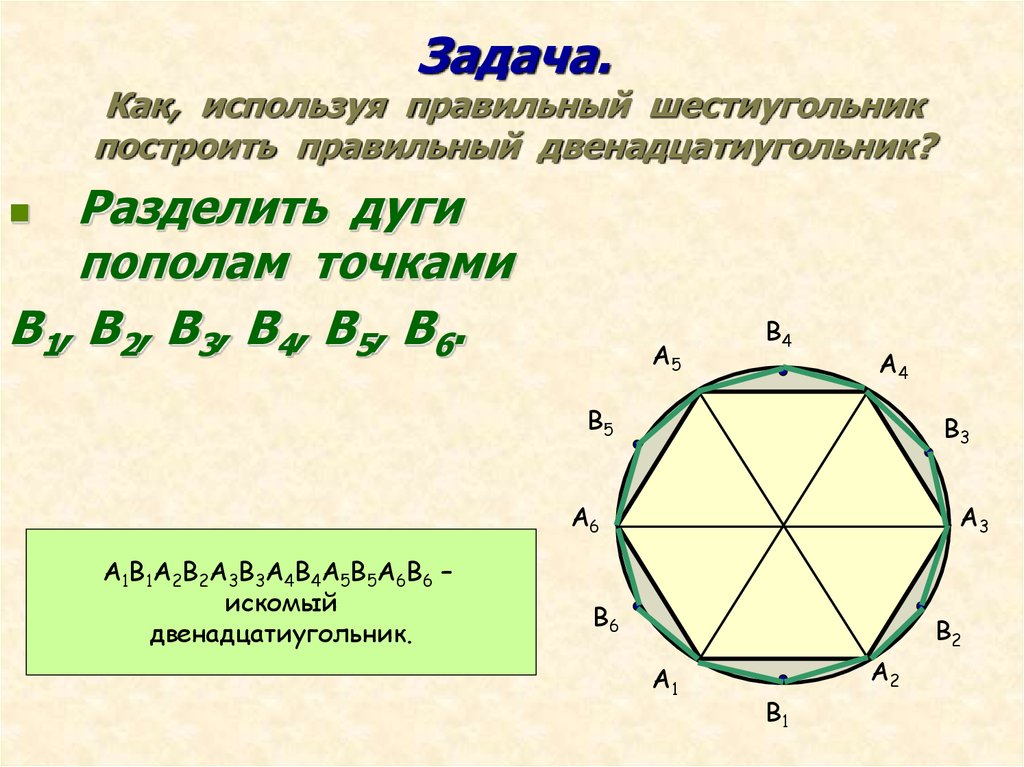
7. Задача. Как, используя правильный шестиугольник построить правильный двенадцатиугольник?

Разделить дуги
пополам точками
В1, В2, В3, В4, В5, В6.
А5
В4
А4
В5
В3
А6
А1В1А2В2А3В3А4В4А5В5А6В6 –
искомый
двенадцатиугольник.
А3
В6
В2
А1
А2
В1

8.

Построение правильного
четырехугольника

9.

10.

11.

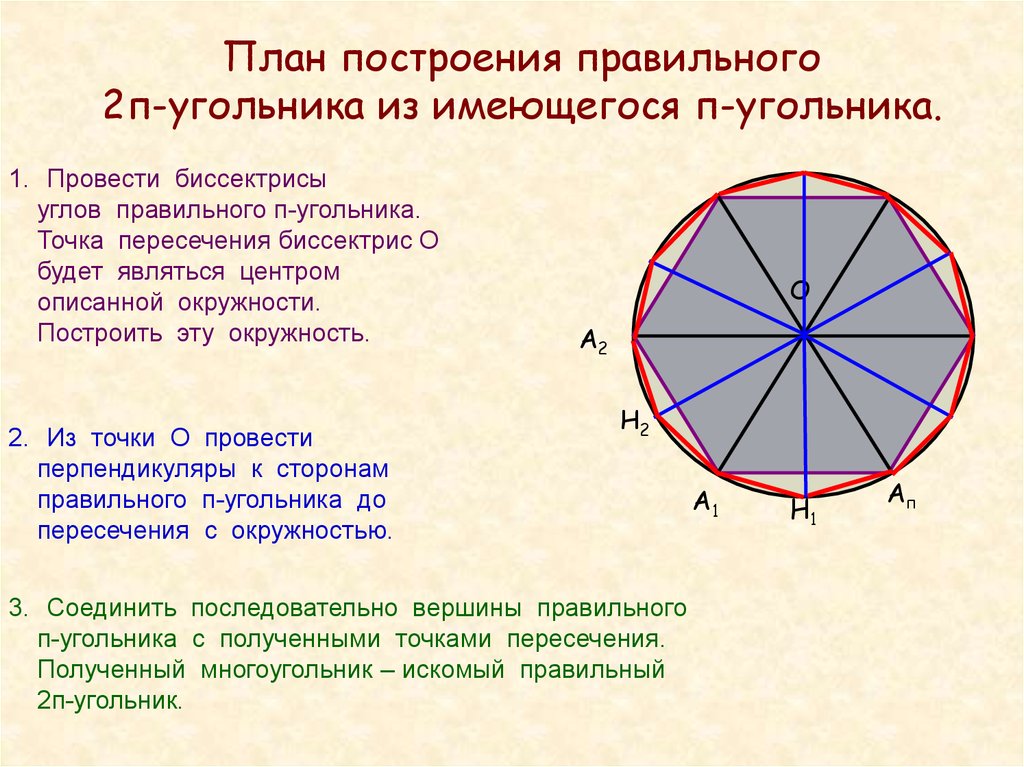
План построения правильного
2п-угольника из имеющегося п-угольника.
1. Провести биссектрисы
углов правильного п-угольника.
Точка пересечения биссектрис О
будет являться центром
описанной окружности.
Построить эту окружность.
2. Из точки О провести
перпендикуляры к сторонам
правильного п-угольника до
пересечения с окружностью.
О
А2
Н2
3. Соединить последовательно вершины правильного
п-угольника с полученными точками пересечения.
Полученный многоугольник – искомый правильный
2п-угольник.
А1
Н1
Ап

12.

Построение правильных многоугольников,
то есть деление окружности на равные
части, позволяло решать практические
задачи:
1)Создание колеса со спицами;
2)Деление циферблата часов;
3)Строительство античных театров;
4)Создание астрономических сооружений

13.

Еще в глубокой древности была поставлена
практическая задача построения
правильного многоугольника с помощью
циркуля и линейки.
Решение этой задачи можно найти в трудах
древнегреческих ученых Архимеда, Евклида,
Пифагора, математиков XYII - XIX веков

14.

Пифагор
Именно в школе ПИФАГОРА зародилось
учение о правильных многоугольниках;
кроме того, пифагорейцы рассмотрели
вопрос покрытия плоскости правильными
многоугольниками.

15.

По некоторым источникам, он
являлся автором сочинения о
правильных многоугольниках,
часто присоединяемого к
"Началам" в качестве XV книги.
Исидор из Милета (532-537 гг.) византийский архитектор и геометр,
построивший вместе с Анфи мием собор Святой Софии в
Константинополе.

16.

Описал построение правильных
3 , 4 , 5 , 6- угольников, построил
правильный 15-угольник

17.

Развитие
готического стиля и
широкое применение витражей в
строительстве соборов также
заставило вернуться к задачам
построения правильных
многоугольников.

18.

Именно Альбрехт Дюрер осуществил
новое построение правильного
пятиугольника, передав потомкам
средневековый способ построения
постоянным раствором циркуля.

19.

Дюрер
занимался фортификацией,
разрабатывая системы
оборонительных сооружений;
Решил задачу построения
правильного восьмиугольника;
Разработал принципы черчения
художественно исполненных букв.

20.

Для своего друга Луки Пачоли
Леонардо, глубоко интересующийся
пропорциями, создал иллюстрации
многогранников, гранями которых
являются правильные
многоугольники.

21.

математик Иоганн Кеплер создал
трактат «Новогодний подарок или о
шестиугольных снежинках»,
опубликованный в 1611 году. В нем он
практически привел первый пример
разбиения плоскости на правильные
шестиугольники.

22.

Доказал возможность построения
правильного 17-угольника. После
этого 19-летний юноша решил
заняться математикой, а не
филологией.

23. Правильные многогранники

1
3
2
4
5