Периодичность тригонометрических функций

1.

Государственное бюджетное профессиональное образовательное
учреждение Самарской области
«Самарский торгово-экономический колледж»
ПЕРИОДИЧНОСТЬ ТРИГОНОМЕТРИЧЕСКИХ
ФУНКЦИЙ
Выполнила
студентка
1 курса 1-ТОВ11 группы
Квасова П.А.
Руководитель
Молчанова Е.В.

2.

ЦЕЛЬ И ЗАДАЧИ
• ЦЕЛЬ
Научиться верно применять
тригонометрические функции при решении
практических измерительных задач; доказать,
что знание основных тригонометрических
функций позволяет решать вопросы во
многих областях науки.
• ЗАДАЧИ
1) Дать определение тригонометрии,
тригонометрическим функциям;
2) Решить некоторые задачи с
использованием тригонометрических
функций;
3) Сделать вывод о проведенной работе.

3.

Функция /(а) называется периодической, если
существует положительное число X 0,
называемое периодом, такое что равенство/(а ± X) =
=/(а) удовлетворяется при любом допустимом
значении аргумента а.
Периодами являются также числа вида пХ, п є
Z, п Ф 0. Наименьший положительный период для
функций sin а и cos а равен 2л, а для функций tga и
ctga равен л.

4.

Функцию у = f(х), х ∈ Х, называют периодической, если
существует такое отличное от нуля число Т, что для любого х из
области определения функции справедливо равенство:
f(х + Т) = f(х) = f(х – Т).
Число Т называют периодом функции у = f(х).
Из этого определения сразу следует, что если Т – период функции
у = f(х), то
2Т, 3Т, 4Т, –Т, –2Т, –3Т, –4Т
– также периоды функций. Значит у периодической функции
бесконечно много периодов. Если Т – период функции, то число
вида kТ, где k – любое целое число, также является периодом
функции.

5.

Возьмём произвольный угол
радиус
ОМ
α
и построим подвижной
единичной окружности такой, что угол,
составленный с осью Ох этим радиусом, равен α.
Если мы к углу
прибавим 2π или 360° (то есть
полный оборот), то углу α + 2π или α + 360° будет
соответствовать то же положение подвижного радиуса ОМ,
Так как синус и косинус угла, составленного с
что для угла α.
осью
Ох
подвижным радиусом
ОМ
единичной
окружности, по сути соответственно ордината
абсцисса х точки М, то
sin (α + 2π) = sin α или
sin (α + 360°) = sin α
и
cos (α + 2π) = cos α или
cos (α + 360°) = cos α.
у
и

6.

Графики периодических функций обладают следующей
особенностью. Если Т – основной период
функции у = f(х), то для построения её графика достаточно
построить ветвь графика на одном из промежутков
оси х длиной Т, а затем осуществить параллельный
перенос этой ветви по оси х на
± Т, ± 2Т, ± 3Т, …
Чаще всего в качестве такого промежутка
длиной Т выбирают промежуток с концами в точках
(–Т/2; 0) и (Т/2; 0) или
(0; 0) и (Т; 0).

7.

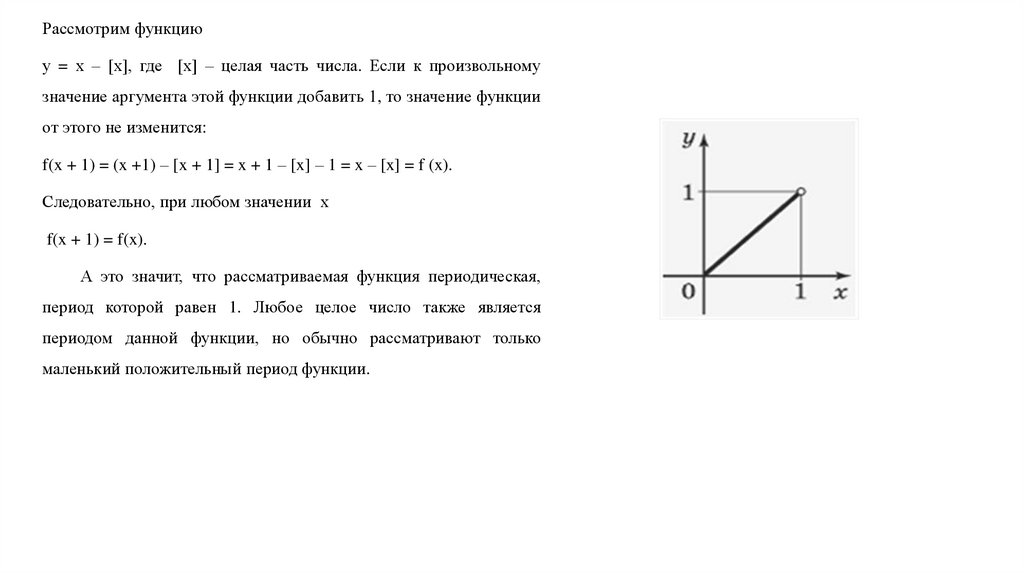
Рассмотрим функцию
у = х – [х], где [х] – целая часть числа. Если к произвольному
значение аргумента этой функции добавить 1, то значение функции
от этого не изменится:
f(x + 1) = (x +1) – [x + 1] = x + 1 – [x] – 1 = x – [x] = f (x).
Следовательно, при любом значении х
f(x + 1) = f(x).
А это значит, что рассматриваемая функция периодическая,
период которой равен 1. Любое целое число также является
периодом данной функции, но обычно рассматривают только
маленький положительный период функции.

8.

Если период функции y = f(x) равен T1, а период
функции y = g(x) равен T2, то период функций
y = f(x) + g(x) и
y = f(x) – g(x)
равен наименьшему числу, при делении которого
на T1 и T2 получаются целые числа.
ПРИМЕР:
Найти период функции
y = 3 sin (x – 2) + 7 соs πx.
РЕШЕНИЕ:
Период функции
y = 3 sin (x – 2)
равен
T1 = 2π/1 = 2π.
Период функции
y = 7 соs πx
равен
T2 = 2π/π = 2.
Периода у функции
y = 3 sin (x – 2) + 7 соs πx
не существует, так как такого числа, при делении
которого на 2π и на 2 получались бы целые числа, нет.
ОТВЕТ:
Периода не существует.

9.

СПАСИБО ЗА ВНИМАНИЕ!!!