Probability and Statistics. Lecture 2. Chapter 3

1.

Probability and Statistics
Lecture 2
Chapter 3

2.

Where are we going?
We have a population (a basket) that we cannot examine but
we want to learn something about it - so we will take a
sample - preferably it will be a random sample.
We will use the sample to estimate the things we wanted to
know about the population - we will use the sample results
to test theories about the population and make some
decisions.
Since the sample is just a part of the population there will be
some uncertainty about the estimates and decisions we
make. To measure and quantify that uncertainty we turn to
PROBABILITY!

3.

4.

The word probability is a commonly used term that relates to the chance
that a particular event will occur when some experiment is performed.
An experiment for us is any process that produces an observation, or
outcome.
We are often concerned with an experiment whose outcome is not
predictable, with certainty, in advance.
Even though the outcome of the experiment will not be known in advance,
we will suppose that the set of all possible outcomes is known. This set of
all possible outcomes of the experiment is called the sample space and is
denoted by S.

5.

Many decisions that we make involve uncertainty and the evaluation of probabilities.
Interpretations of Probability
Example: Roll a fair die possible outcomes = {
}
Before you roll the die do you know which one will occur?
What is the probability that the outcome will be a ‘4’? __________ Why?
A few ways to think about PROBABILITY:
(1)
Personal or Subjective Probability
P(A) = the degree to which a given individual believes that the event A will happen.
(2)
Long term relative frequency
P(A) = proportion of times ‘A’ occurs if the random experiment (circumstance) is repeated many,
many times.
(3) Basket Model
P(A) = proportion of
balls in the basket
that have an ‘A’ on
them.
10 balls in the basket: 3
blue and 7 white
One ball will be
selected at random.
What is P(blue)?
______________

6.

Some examples of experiments and their sample spaces are as follows.
(a) If the outcome of the experiment is the gender of a child, then S = {g, b} where
outcome g means that the child is a girl and b that it is a boy.
(b) If the experiment consists of flipping two coins and noting whether they land heads
or tails, then
S = {(H,H), (H, T), (T,H), (T, T)}
(d) Consider an experiment that consists of rolling two six-sided dice and noting the
sides facing up. If we let (i, j ) denote the outcome in
which die 1 has value i and die 2 has value j , then the sample space of this experiment
is

7.

8.

Any set of outcomes of the experiment is called an event.
That is, an event is a subset of the sample space. Events will be denoted by the capital
letters A,B,C, and so on.
In Example 4.1(d), if
A = {(1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1)}
then A is the event that the sum of the dice is 7.

9.

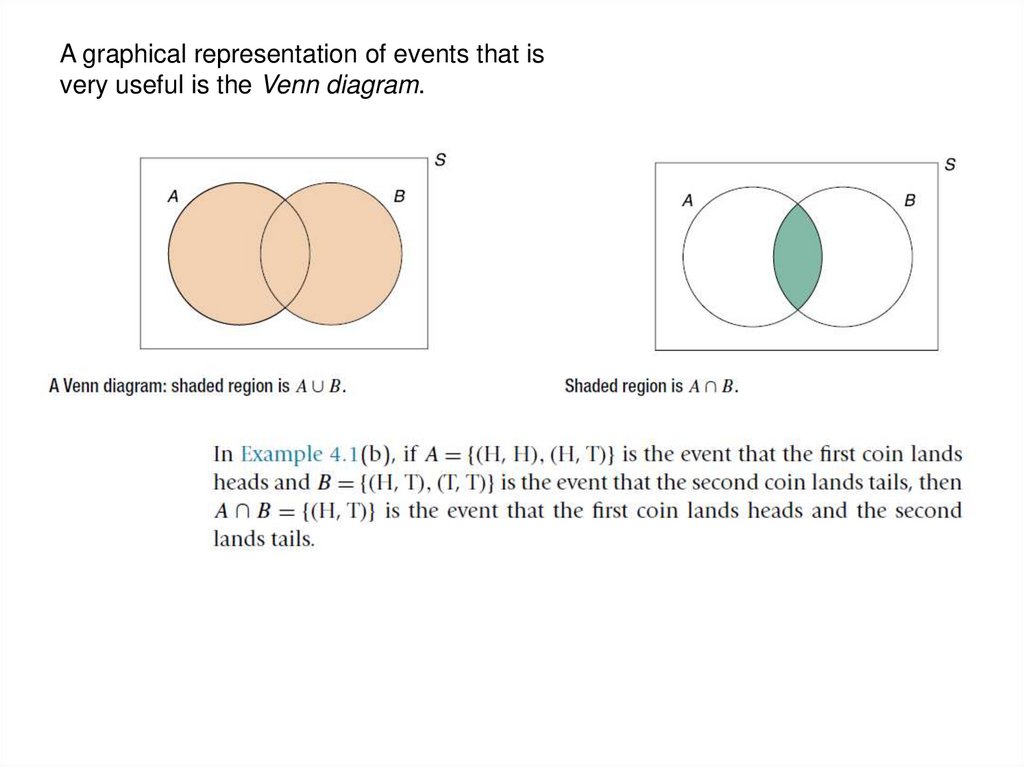
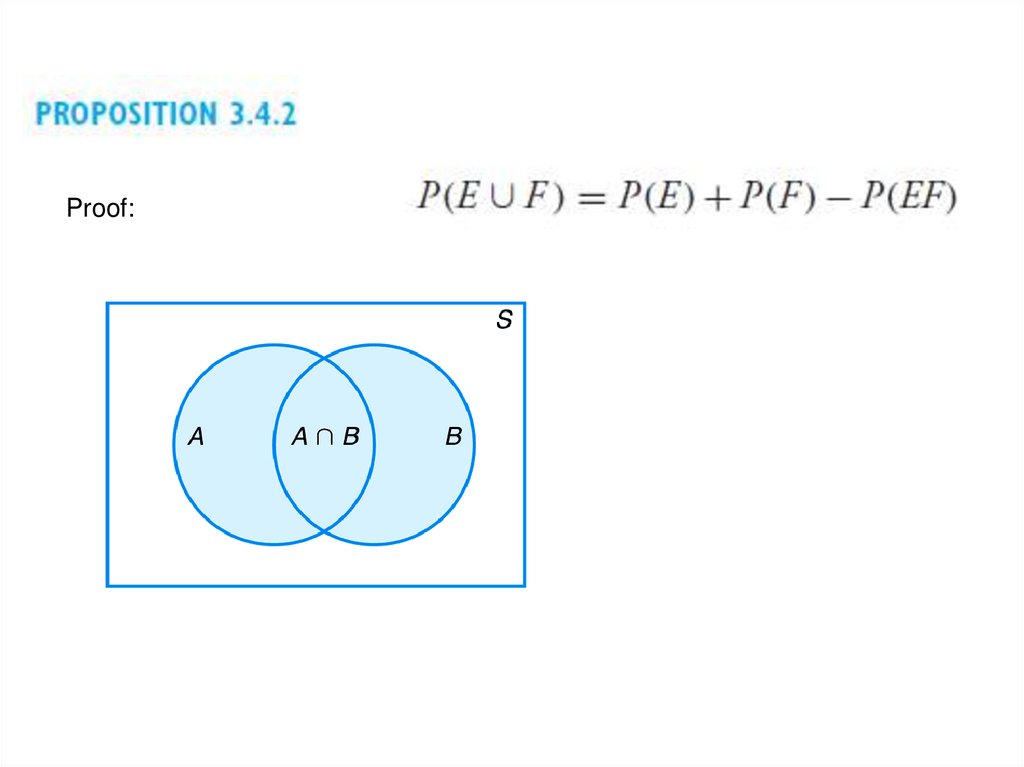
A graphical representation of events that is
very useful is the Venn diagram.

10.

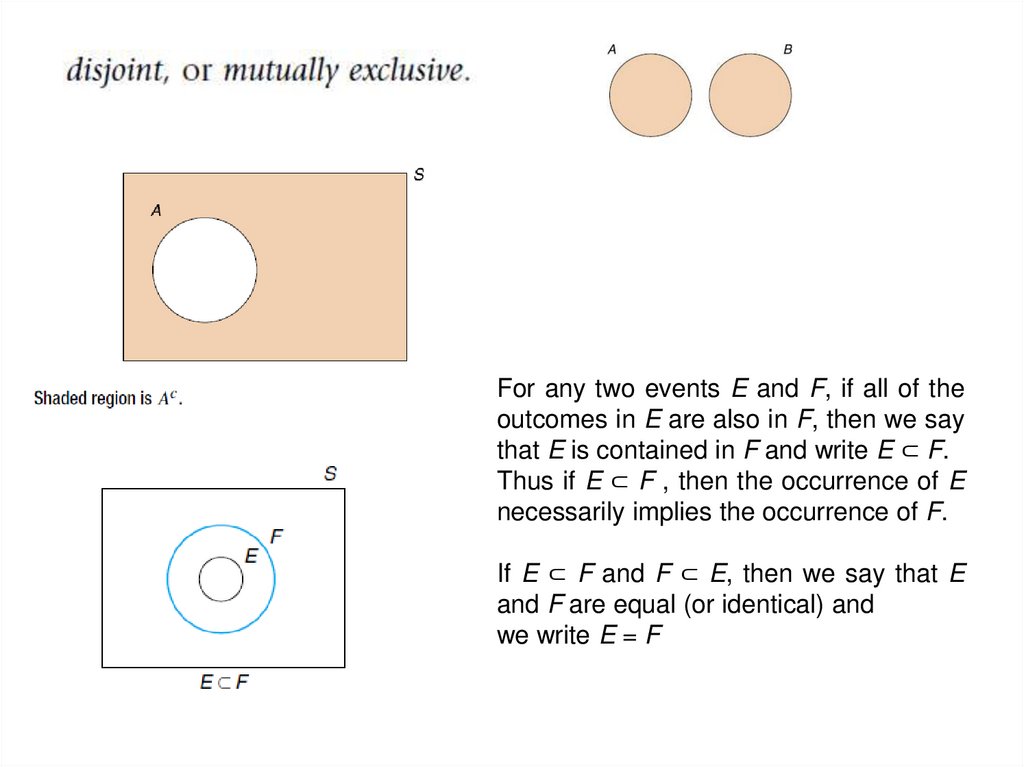
For any two events E and F, if all of the
outcomes in E are also in F, then we say
that E is contained in F and write E ⊂ F.
Thus if E ⊂ F , then the occurrence of E
necessarily implies the occurrence of F.
If E ⊂ F and F ⊂ E, then we say that E
and F are equal (or identical) and
we write E = F

11.

12.

13.

Proof:

14.

15.

SAMPLE SPACES HAVING EQUALLY LIKELY OUTCOMES
For a large number of experiments, it is natural to assume that
each point in the sample space is equally likely to occur.
BASIC PRINCIPLE OF COUNTING
Suppose that two experiments are to be performed. Then if experiment 1 can result in
any one of m possible outcomes and if, for each outcome of experiment 1, there are n
possible outcomes of experiment 2, then together there are mn possible outcomes of the
two experiments
Example: two dice rolled, two coins tossed.

16.

Generalized Basic Principle of Counting
If r experiments that are to be performed are such that the first one may result in
any of n1 possible outcomes, and if for each of these n1 possible outcomes there
are n2 possible outcomes of the second experiment, and if for each of the
possible outcomes of the first two experiments there are n3 possible outcomes of
the third experiment, and if, . . . , then there are a total of n1 · n2 · · · nr possible
outcomes of the r experiments.
n! = n(n−1)(n−2) · · · 3 · 2 · 1
Example 2.17: How many even four-digit numbers can be formed from the
digits
0, 1, 2, 5, 6, and 9 if each digit can be used only once?

17.

As an illustration of this, let us determine the number of different ways
n distinct objects can be arranged in a linear order.
For instance, how many different ordered arrangements
of the letters a, b, c are possible? By direct enumeration we see that
there are 6; namely, abc, acb, bac, bca, cab, cba. Each one of these
ordered arrangements is known as a permutation.

18.

Suppose now that we are interested in determining the number of
different groups of r objects that could be formed from a total of n
objects.
Suppose now that we are interested in determining the number of
different groups of r objects that could be formed from a total of n
objects.

19.

20.

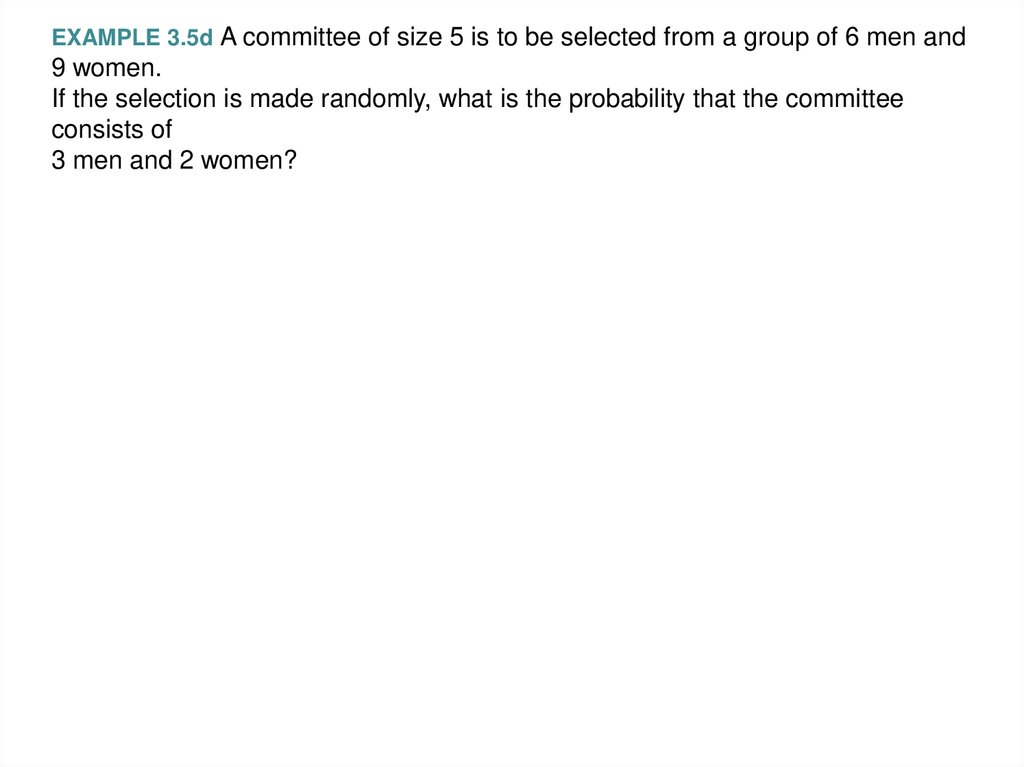
EXAMPLE 3.5d A committee of size 5 is to be selected from a group of 6 men and
9 women.
If the selection is made randomly, what is the probability that the committee
consists of
3 men and 2 women?

21.

EXAMPLE 3.5f
A basketball team consists of 6 black and 6 white players. The players are to be paired in
groups of two for the purpose of determining roommates.
If the pairings are done at random, what is the probability that none of the black players
will have a white roommate?

22.

23.

CONDITIONAL PROBABILITY
In this section, we introduce one of the most important concepts in all of
probability theory —that of conditional probability. Its importance is twofold.
In the first place, we are often interested in calculating probabilities when some
partial information concerning the result of the experiment is available,
/or in recalculating them in light of additional information.
In such situations, the desired probabilities are conditional ones.
Second, as a kind of a bonus, it often turns out that the easiest way to compute
the probability of an event is to first “condition” on the occurrence or
nonoccurrence of a secondary event.
the conditional probability of E given that F has occurred, and is
denoted by
P(E|F )
=(Number of points in EF) /
Number of points in F
Restatement of the definition
P(EF)=P(F)* P(E|F)

24.

25.

26.

Example. A class consisting of 4 graduate and 12 undergraduate students is
randomly divided into 4 groups of 4.
What is the probability that each group has a graduate student?

27.

Total probability

28.

You take part in a chess tournament where your probability of winning is 0,3
against half the players (type 1), 0,4 against a ¼ of the players (type 2), and 0,5
against the remaining players (type 3) . You play a game against a randomly
chosen opponent. What is the probability of winning?

29.

REVERSE
P(A|B) vc P(B|A)
In Chess problem - Suppose that you win. What is the
probability that you had an opponent of type 1?

30.

EXAMPLE 3.7c In answering a question on a multiple-choice test, a student
either knows the answer or she guesses. Let p be the probability that she
knows the answer and 1−p the probability that she guesses. Assume that a
student who guesses at the answer will be correct with probability 1/m,
where m is the number of multiple-choice alternatives.
What is the conditional probability that a student knew the answer to a
question given that she answered it correctly?
Bayes Rule

31.

Suppose we have 3 cards identical in form except that both sides of the 1st
card are colored red; both sides of the 2nd card are colored black; 3rd card –
one side red, other side is black
The three cards mixed up in hat, and one card is
randomly selected and put down on the ground.
If the upper side of the chosen card is red, what
is the probability that the other side is colored
black?

32.

Using conditional probability for modeling
If an aircraft is present in a certain region, a radar correctly registers its
presence with probability 0,99.
If it is not present, the radar falsely registers an aircraft presence with
probability 0,1.
Assume that aircraft is present with probability p=0,05.
Find:
a) Probability of false alarm (false indication of presence)
b) Probability of missed detection (i.e. nothing registered even though is
present)

33.

Independence
We introduced conditional probability to catch the partial information that event
B provides about event A
P(A|B)
If occurrence of event B has no influence to A
P(A|B)= P(A)
we say that A is independent of B
P(AB)= P(A) P(B)

34.

Theorem. If E and F are independent , then
E and