Similar presentations:
Elements of probability. (Lecture 3)
1. Lecture #_3
Lecture #_3Elements of probability
1
2.
Definition 1A simple event is an outcome of an experiment that
can not be decomposed into a simpler outcome
Example 1. Tossing 1 fair coin
1 , 2
1 head (H)
2 tail (T)
2
3.
Example 2. Tossing 3 fair coins at once1 , 2 , 3 , 4 , 5 , 6 , 7 , 8
1 HHH 5 TTT
2 TTH 6 HHT
3 THT 7 HTH
4 HTT 8 THH
3
4.
A random variable X( ) is a function of , e.g., X( ) isthe number of heads in one trial, hence,
X( 1 ) 3, X( 6 ) X( 7 ) X( 8 ) 2,
X( 2 ) X( 3 ) X( 4 ) 1, X( 5 ) 0
Definition 2
An event is a collection of one or more simple events
4
5.
Example 3.A 2 Heads in one toss
A ω6,ω7 ,ω8
B More than one H in a trial
B ω1,ω6,ω7 ,ω8
C Exactly 2 tails (T)
C ω2,ω3,ω4
D At least one H or one T
D ω1,ω2,ω3,ω4,ω5,ω6,ω7 ,ω8
5
6.
Definition 3The sample space of an experiment is the collection of
all possible simple events
Denote it by Ω
{ 1 , 2 }
For example 1:
For example 2 : { 1 , 2 , ..., 8 }
6
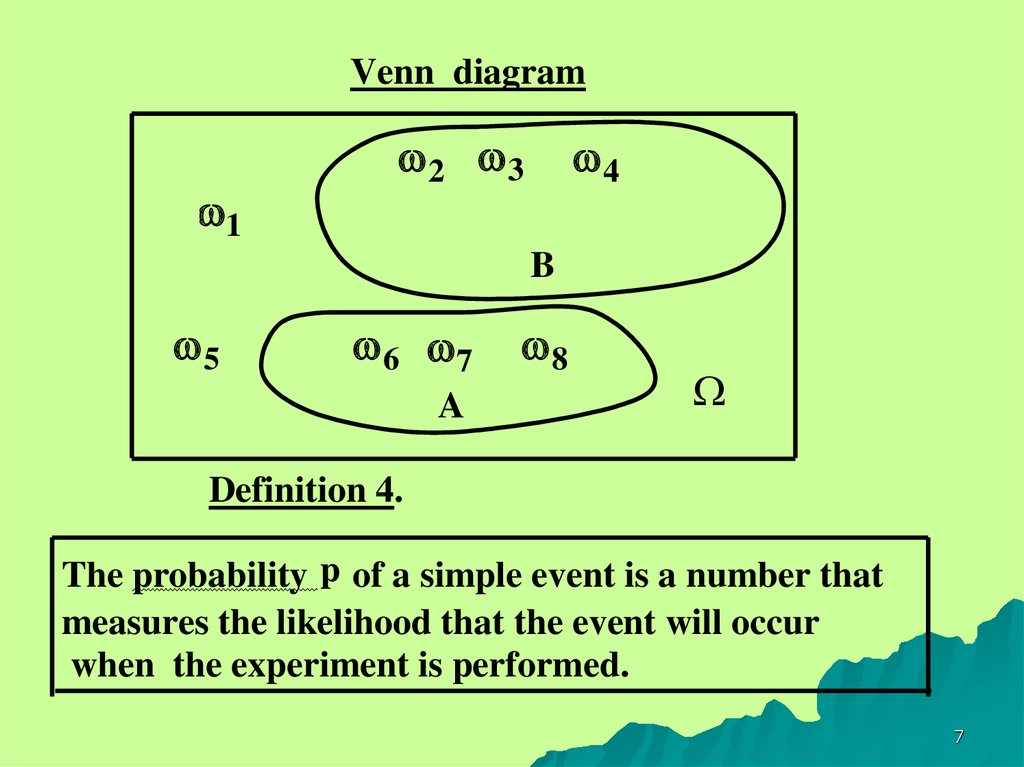
7.
Venn diagram1
2 3
4
B
5
6 7
A
8
Definition 4.
The probability p of a simple event is a number that
measures the likelihood that the event will occur
when the experiment is performed.
7
8.
I.Classical definition of probabilities. If one has n
equiprobable simple events 1 , ..., n , then the
probability
of
p( A)
A i1 , i 2 , ..., im
containing m simple events is
m
P( A )
n
Evidently, that P( ) 1.
8
9.
II. We may take p being equal to the relative frequencyf /n of a simple ith event if n is very large.
i
III. We may select p based on a priori knowledge of a
situation under study.
The case III is more frequently occurred. We guess or
formulate a hypothesis H concerning p and, using
statistics, test this hypothesis based on realizations
( x1 , ..., x n ) of a sample X n { X1 , ..., X n }.
Definition 5
The probability P( A) of an event A is calculated
by summing the probabilities of the simple events
belonging to A .
9
10. Steps for calculating probabilities
1. List the simple events2. Assign probabilities to simple events
3. Determine the number of simple events
containing in the event
4. Sum the simple event probabilities to
obtain the event probability
10
11.
For example 2p(ω i ) 1/8, i 1,8
p(A) p(2H) p{ω 6 ,ω 7 ,ω 8 }
1
8
1
8
1
8
3
8
p(B) P(more than 1H)
p{ω1 ,ω 6 ,ω 7 ,ω 8 }
1
8
1
8
1
8
1
8
1
2
p(D) p(Ω) 1 (certain event)
11
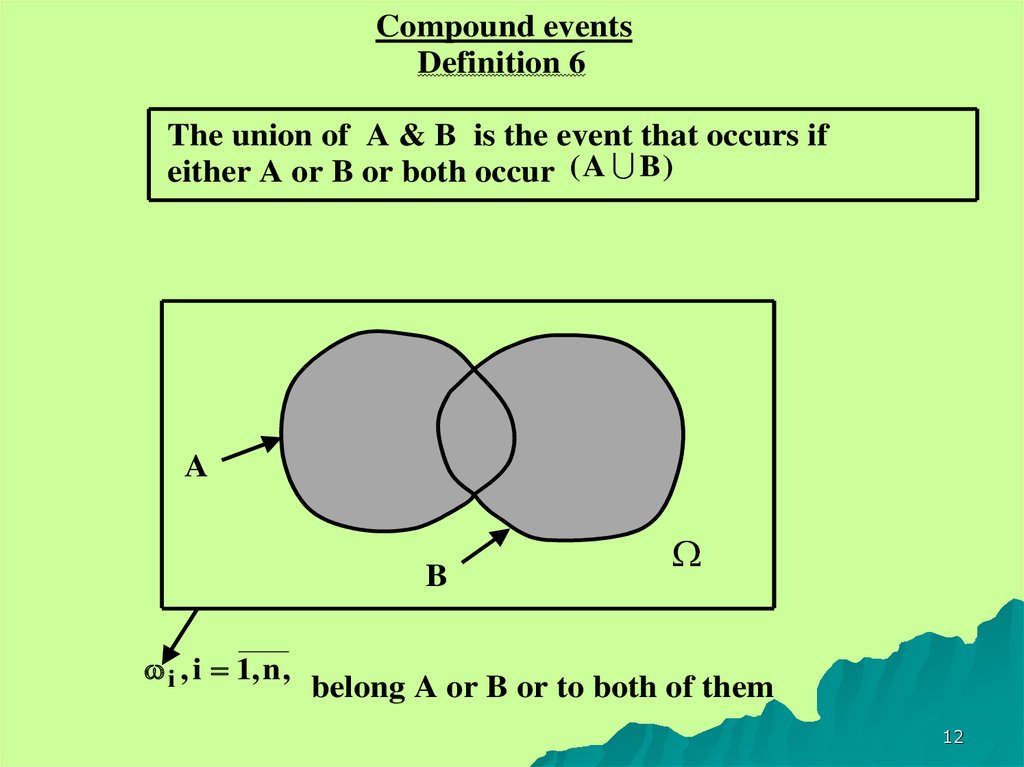
12.
Compound eventsDefinition 6
The union of A & B is the event that occurs if
either A or B or both occur ( A B )
A
B
i , i 1, n ,
belong A or B or to both of them
12
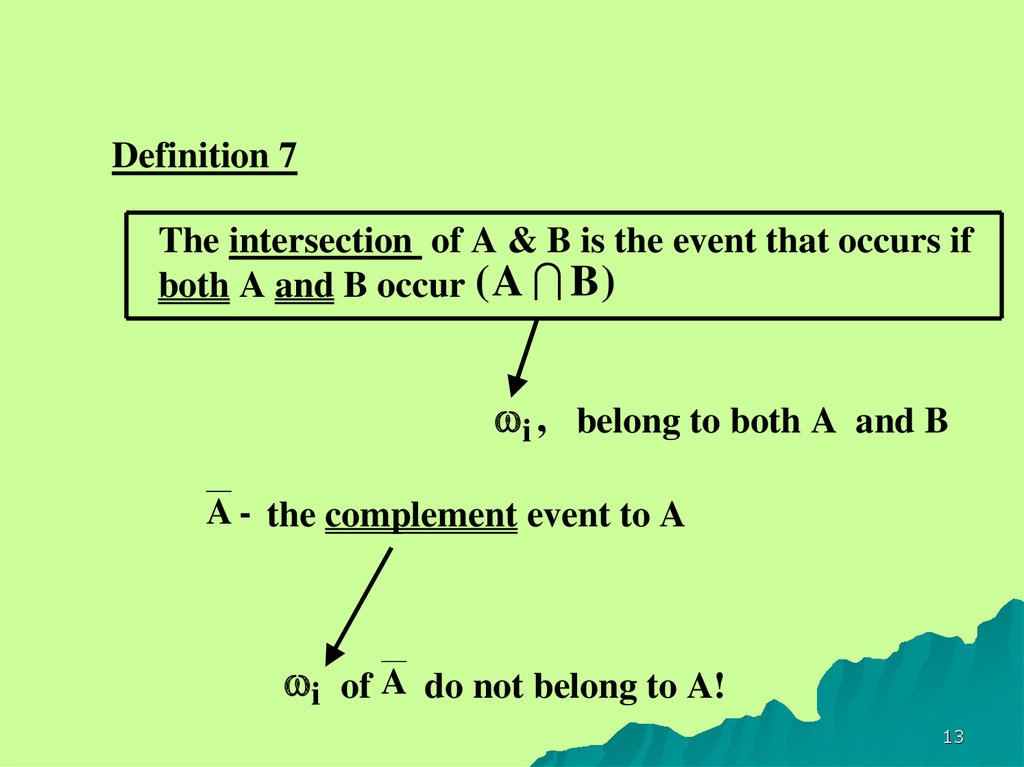
13.
Definition 7The intersection of A & B is the event that occurs if
both A and B occur ( A B )
i , belong to both A and B
A - the complement event to A
i of A do not belong to A!
13
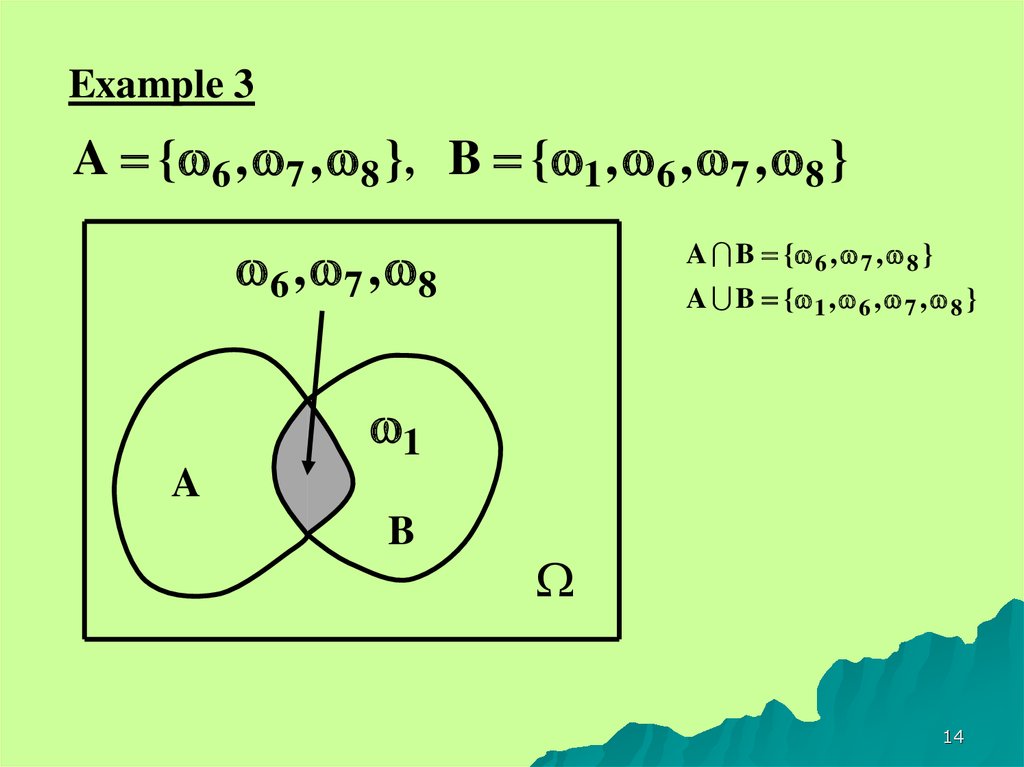
14.
Example 3A { 6 , 7 , 8 }, B { 1 , 6 , 7 , 8 }
6 , 7 , 8
A B { 6 , 7 , 8 }
A B { 1 , 6 , 7 , 8 }
1
A
B
14
15.
Let a set { 1 , ..., n } be given, then all possibleevents (combinations of i th ) (empty set,
corresponding to the improbable event) is algebra S of
events
15
16.
If two events A & B are mutually exclusive(incompatible), then
P( A B) P( A) P(B).
Suppose we have a target. A shooter produced a shot.
A to hit the target
B fail to hit
A&B are incompatible
P( A) P(B) 1
A B is the certain
event
16
17.
Axioms of probabilityFor every (a set of all possible simple events) and S
(algebra of events) we postulate
1) Axiom 1. For every S P(A)
2) Axiom 2. P( ) 1
-is certain event
3) Axiom 3. If S and B S are incompatible, then
P( A B) P( A) P(B).
The following two rules are consequences of axioms:
17
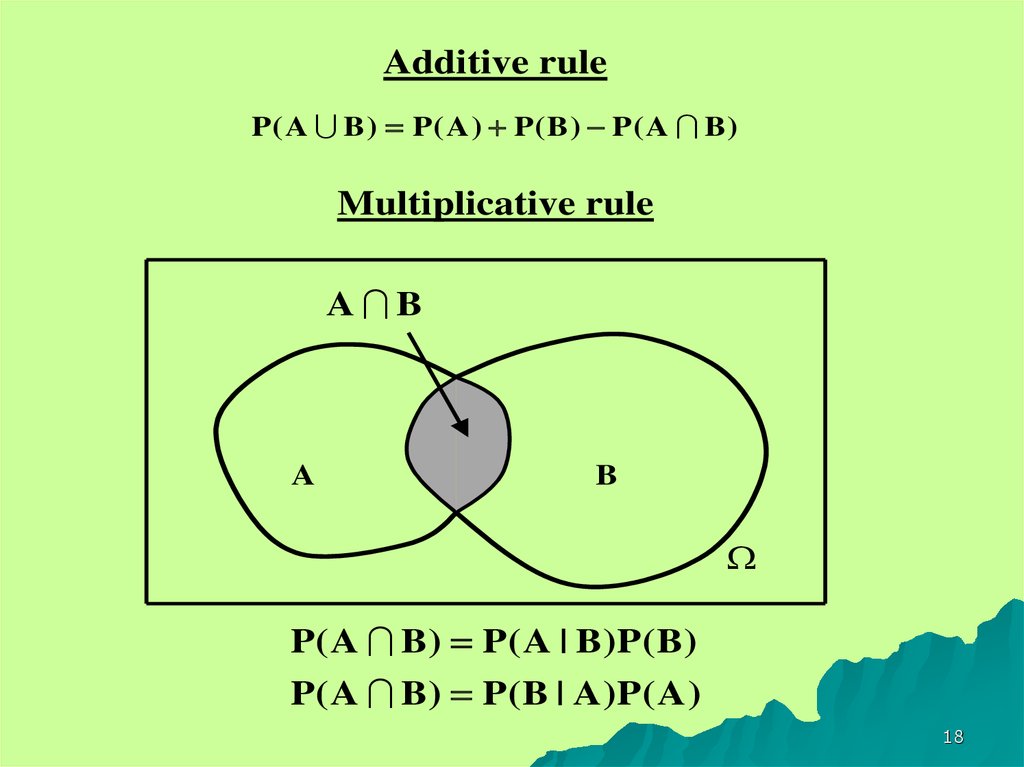
18.
Additive ruleP( A B ) P( A ) P(B ) P( A B )
Multiplicative rule
A B
A
B
P( A B ) P ( A | B )P ( B )
P( A B ) P ( B | A )P ( A )
18
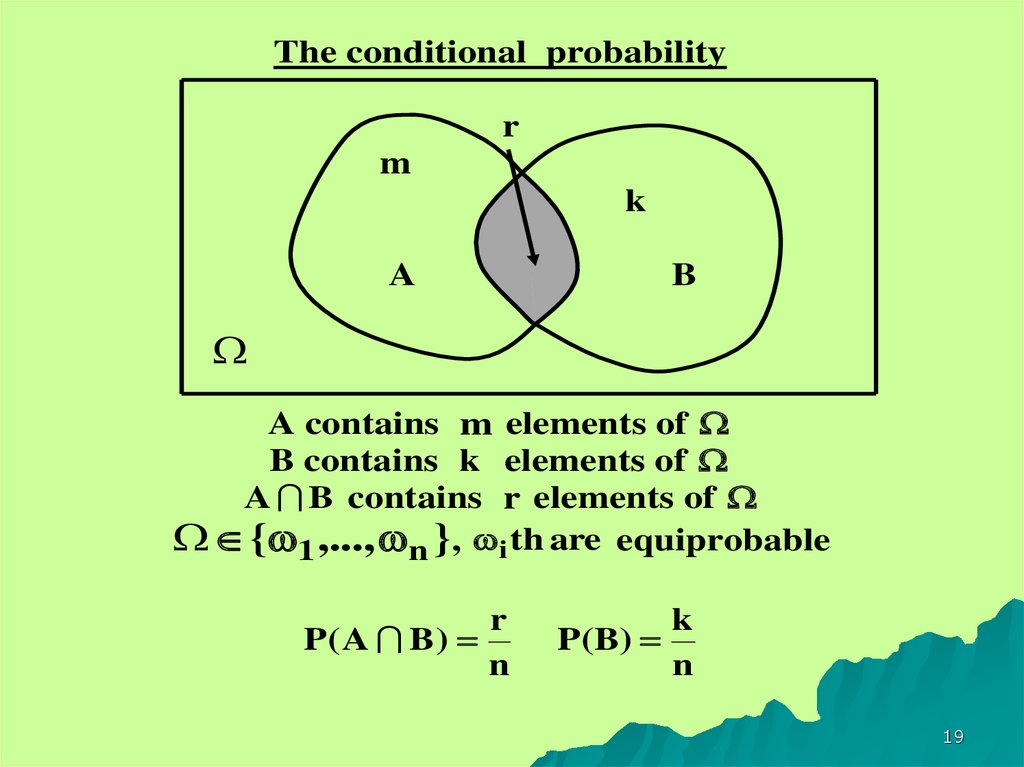
19.
The conditional probabilityr
m
k
A
B
A contains m elements of
B contains k elements of
A B contains r elements of
{ 1 ,..., n }, i th are equiprobable
r
P( A B )
n
k
P(B)
n
19
20.
Let the event B occurred. What is the prob. for A tooccur?
r r / n P( A B )
P( A | B )
k k /n
P( B )
P( A B )
P( A | B )
P( B )
20
21.
IndependenceEvents A and B are independent if the assumption
that B has occurred does not alter the probability that
A occurs, or if
P (A | B) = P (A)
or
P (B | A) = P (B)
Otherwise, A&B are dependent
21
22.
Example 2A 6 , 7 , 8 two H in one tos sin g
B 1 , 6 , 7 , 8 than 1 H in one tossing
3
4
8
P(A)
P(B)
P( ) 1
8
8
8
A B 6 , 7 , 8 A
3
P( A B ) P( A )
8
3 4 3
P( A B ) P( A | B )P( B )
4 8 8
3 1 3
3
P( A ) P( B ) P( A B )
8 2 16
8
22
23.
Hence, A and B are dependentP( A B ) 3 / 8 3
3
P( A | B )
P ( A ) !!
P( B )
1/ 2 4
8
For independent events
P(A B) = P(A) P(B)
23
24.
Random variable X( (discrete)X( is the number of H for example 2. From the
symmetry of a coin we may suppose that the
probability p to obtain a head in one trial is
p 1 / 2.(q 1 / 2 1 p) . Then
3 k 3 k
P ( X k ) p q
,
k
k 0,1,2,3.
2
3 2
3 1 1
1 1 3
P ( A ) P ( X 2 )
3
4 2 8
2 2 2
P(B ) P( X 1) P( X 2) P( X 3)
3
0
3
3 1 1
3 1 1
8 3 2 2
8 8 2
24
25.
Events (X=2) & (X=3) are mutually exclusive, henceP ((X=2) (X=3)) = P (X=2)+P (X=3).
We may consider P(X=k) as both known and known
within the unknown parameter p.
25
26.
Population moments (discrete case)Let P (X = k) be the p. d. of X, k {set of discrete
numbers}= .
P( X k ) 1
k K
Definition 9
The initial population moment of P (X = k) of order m
is
m k m P( X k ) E( X m )
k K
EX m - expectation of Xm or
expected value of Xm
26
27.
Definition 10The central population moment of P (X = k) of order
m is
m (k EX)m P( X k ) E( X EX)m
k K
Definition 11 (p.210)
The mean or expected value of a discrete r. v. X is
EX kP( X k )
k K
27
28.
Definition 12The variance of a discrete random variable X is
2 E( X ) 2 (k ) 2 P( X k )
k K
28
29.
Example Binomial distributionP (X k )
n
k
pk (1 p)n k , k=0,n
K 0,1, ...,n
n
EX k
k 0
n
k
pk (1 p)n k
n
kn!
pk (1 p)n k
k 1 k !(n k )!
n
n(n 1)!
p pk 1qn k
k 1 (k 1)!(n k )!
k 1
n
np
n 1
k 1
pk 1qn k
k 1 r k r 1
29
30.
p qnp,
r 0
n 1
n 1
r (n 1) r
n 1
(p q)
1
r p q
r 0
n 1
np
n 1
r
r (n 1) r
Thus,
EX np
By the same lines
2
E(X
)
npq
S tan dard deviation
npq (1a)
2
30























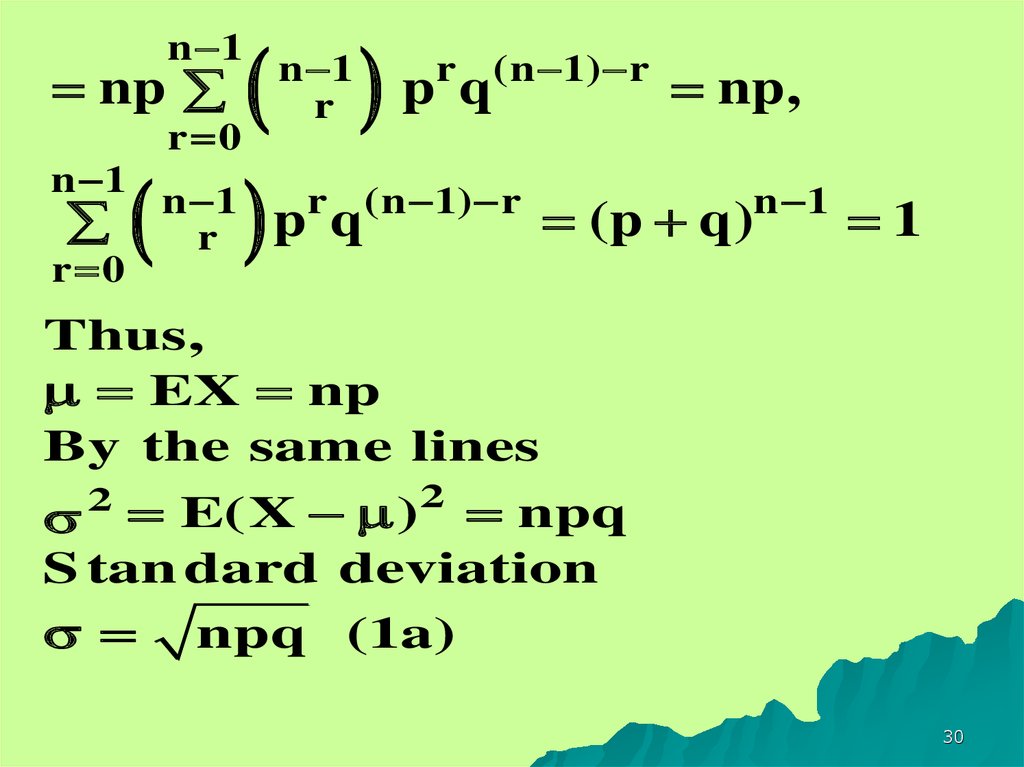
 mathematics
mathematics








