Векторы в пространстве

1.

Презентация на
тему:
Векторы в
пространстве.
Подготовил студент группы "2ХТ1" Туленов Максим

2.

Понятие вектора в пространстве.
• Вектором называется отрезок, для которого
указано, какой из его концов считается началом,
а какой - концом.
Направление вектора на рисунках отмечается
стрелкой.
• Любая точка пространства также может
рассматриваться как вектор. Такой вектор
называют нулевым. Начало и конец нулевого
вектора совпадают, и он не имеет какого либо
определённого направления.
Вектора обозначаются стрелками сверху, например:
Вектор с началом A и концом B обозначают как AB

3.

Длинна вектора.
• Длинна вектора равна длине
соответствующего ему отрезка.
AB = AB
• Векторы называются равными,
если они сонаправлены и их
длины равны.
• Два вектора называются
противоположными, если их
длины равны и они
противоположно направлены.

4.

Сложение и вычитание векторов.
• Для сложения векторов пользуются
правилом треугольника, которое
представлено на рисунке справа.
• Правило треугольника так же
применяется и для вычитания
векторов. Разностью векторов a и b
называется такой вектор, сумма
которого с вектором b равна
вектору a.

5.

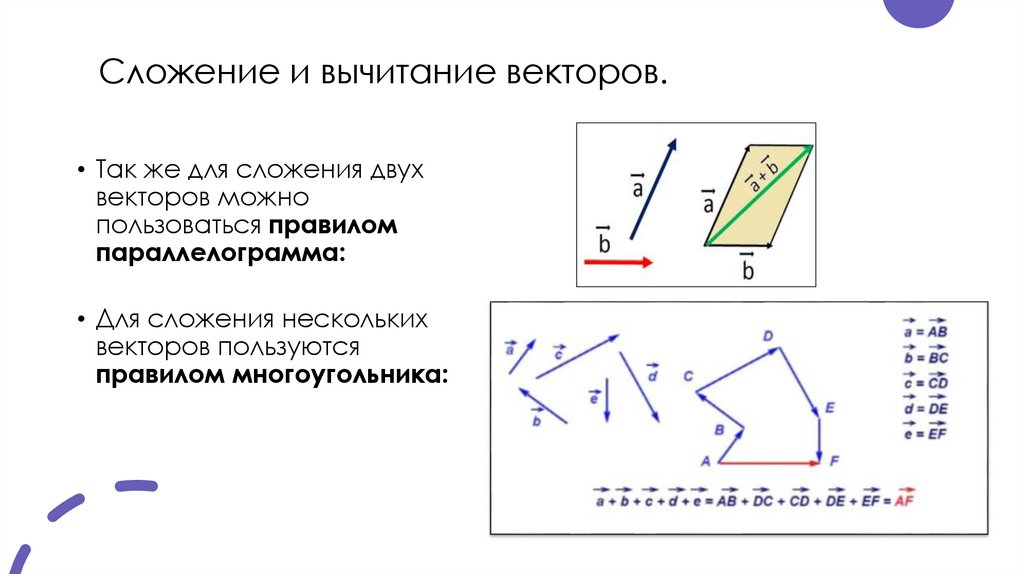
Сложение и вычитание векторов.
• Так же для сложения двух
векторов можно
пользоваться правилом
параллелограмма:
• Для сложения нескольких
векторов пользуются
правилом многоугольника:

6.

Умножение вектора
на число
• Произведением ненулевого
вектора a на число k называется
такой вектор b длина которого
равна k*a причем векторы a и b
сонаправлены про k > 0 и
противоположно направлены
про k < 0
• Произведением нулевого
вектора на любое число
считается нулевой вектор

7.

Коллинеарные и
компланарные векторы.
• Два ненулевых вектора называются
коллинеарными, если они лежат на
одной прямой или параллельных
прямых.
• Векторы называют компланарными,
если при откладывании их от одной
и той же точки они будут лежать в
одной плоскости. Другими словами,
векторы называются
компланарными, если имеются
равные им векторы, лежащие в
одной плоскости.

8.

Операции над
векторами
• Для векторов справедливы
переместительный,
сочетательный и
распределительный законы.
• A+B = B+A
• (A+B)+C = A+(B+C)
• (k*l)*A = k*(l*A)
• K*(A+B) = k*A + k*B
• (k+l)*A = k*A + l*A
• (A+B)*C = A*C + B*C
• K(A*B) = (kA)*B

9.

Применение векторов
• Помимо математики, векторы применяются во многих
науках. В физике встречается немало важных величин,
являющихся векторами, например сила, положение, скорость,
ускорение, вращающий момент, импульс, напряженность
электрического и магнитного полей. На языке векторов
формулируются основные законы механики и
электродинамики.
Так же с вектора используются в таких науках как биология,
химия, экономика.
Векторы можно встретить и в обычной жизни, например на
знаках дорожного движения.

10.

Спасибо за
просмотр!