Векторы в пространстве

1. Векторы в пространстве

2. Понятие вектора

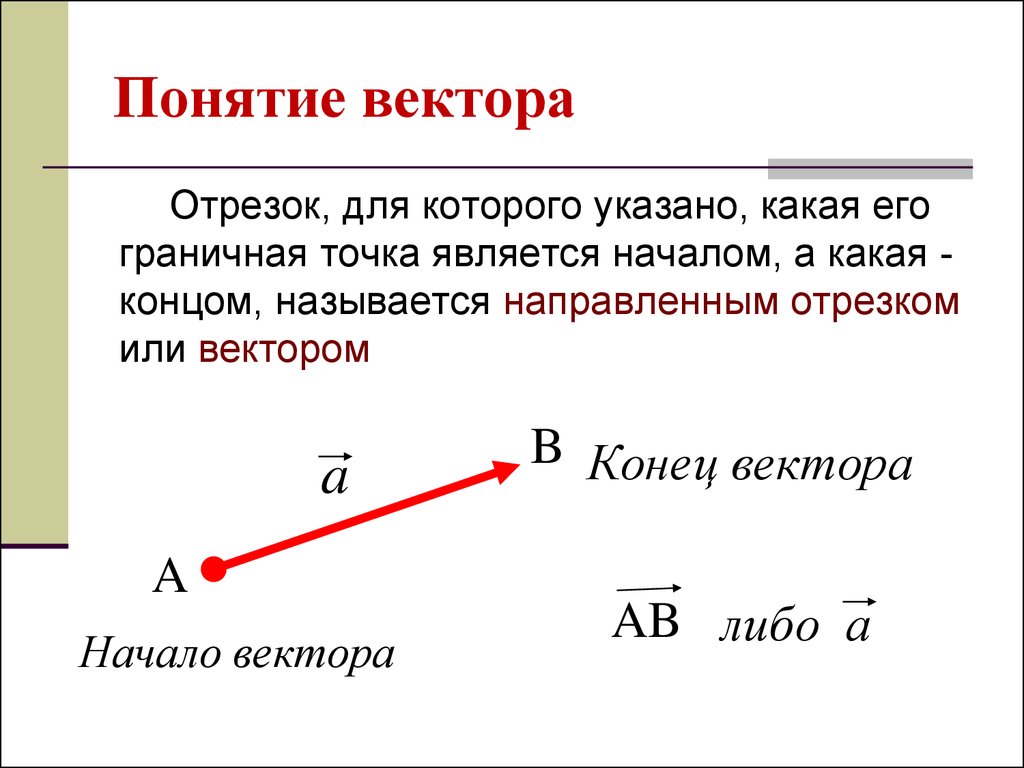
Отрезок, для которого указано, какая его
граничная точка является началом, а какая концом, называется направленным отрезком
или вектором
a
A
Начало вектора
B Конец вектора
AB либо а

3. Длина вектора

Е
К
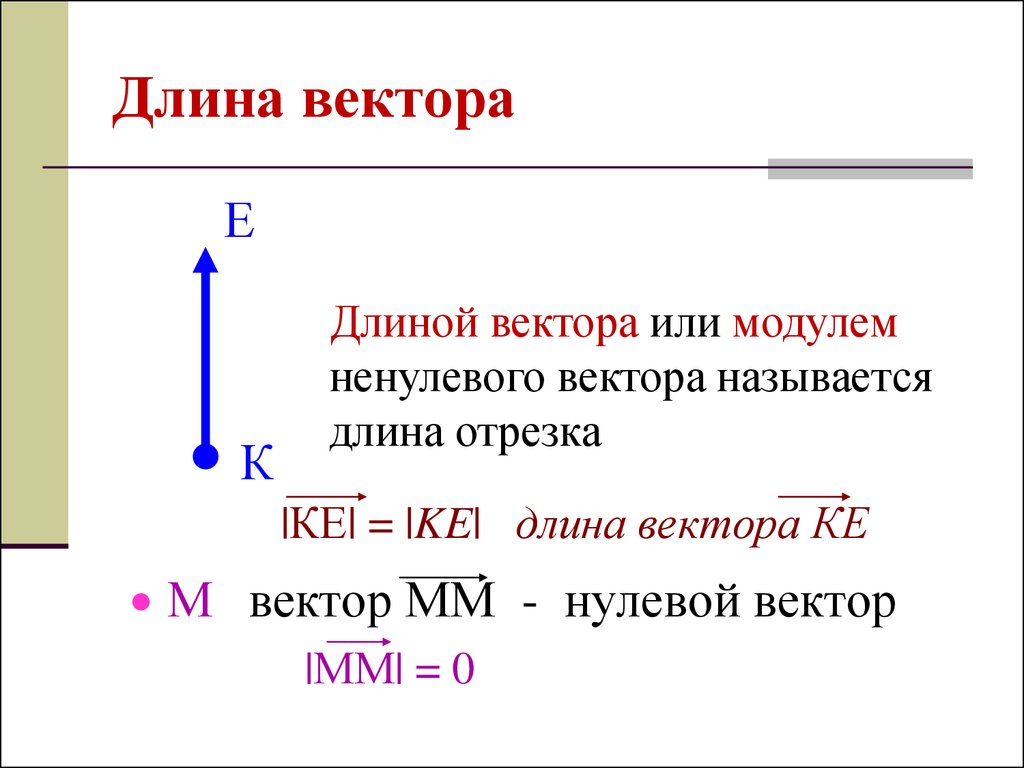
Длиной вектора или модулем
ненулевого вектора называется
длина отрезка
|КЕ| = |KE| длина вектора КЕ
М вектор ММ - нулевой вектор
|ММ| = 0

4. Коллинеарные векторы

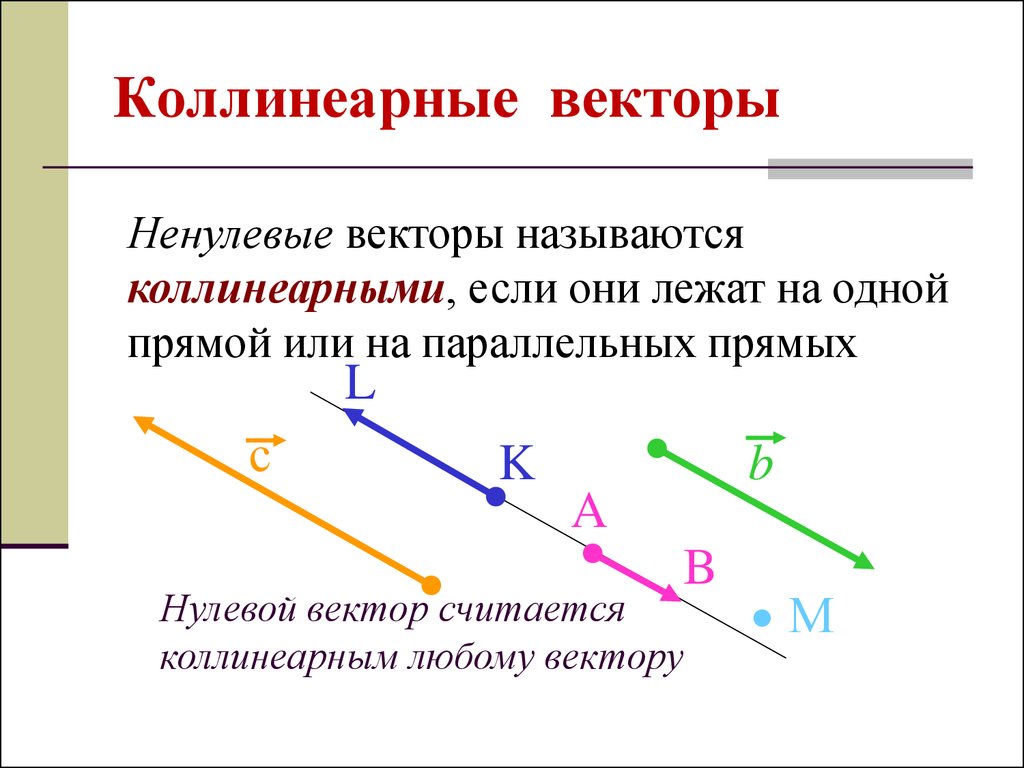
Ненулевые векторы называются
коллинеарными, если они лежат на одной
прямой или на параллельных прямых
L
с
K
b
A
Нулевой вектор считается
коллинеарным любому вектору
B
М

5. Сонаправленные векторы

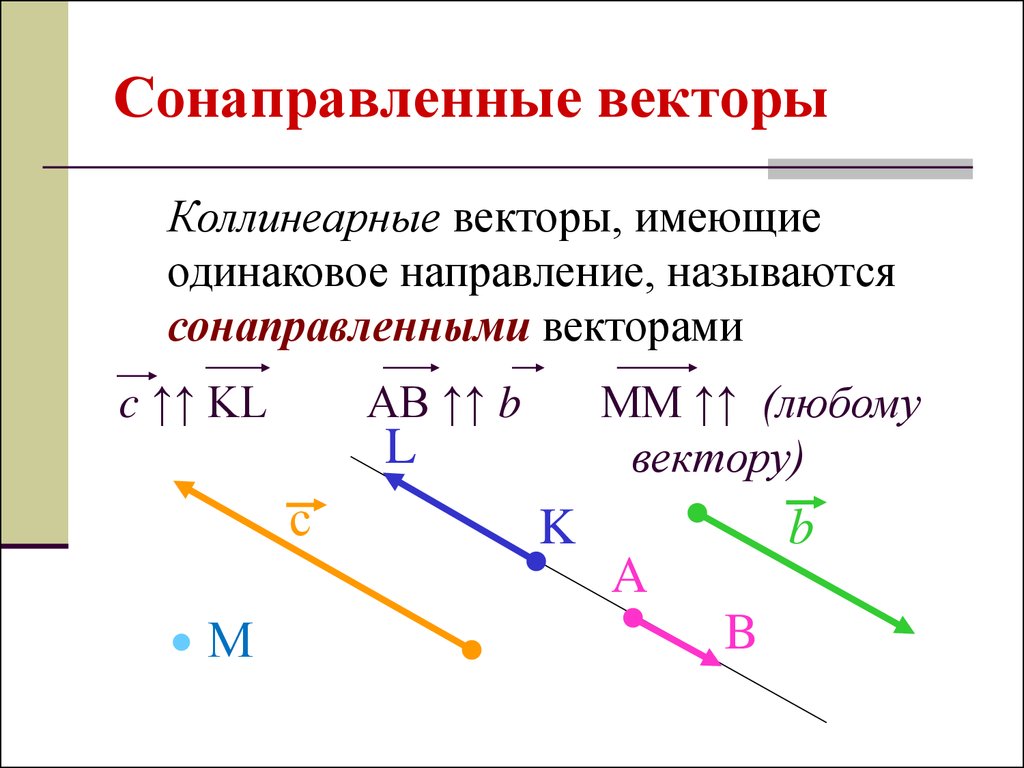
Коллинеарные векторы, имеющие
одинаковое направление, называются
сонаправленными векторами
c ↑↑ KL
AB ↑↑ b
MM ↑↑ (любому
вектору)
L
с
K
b
A
М
B

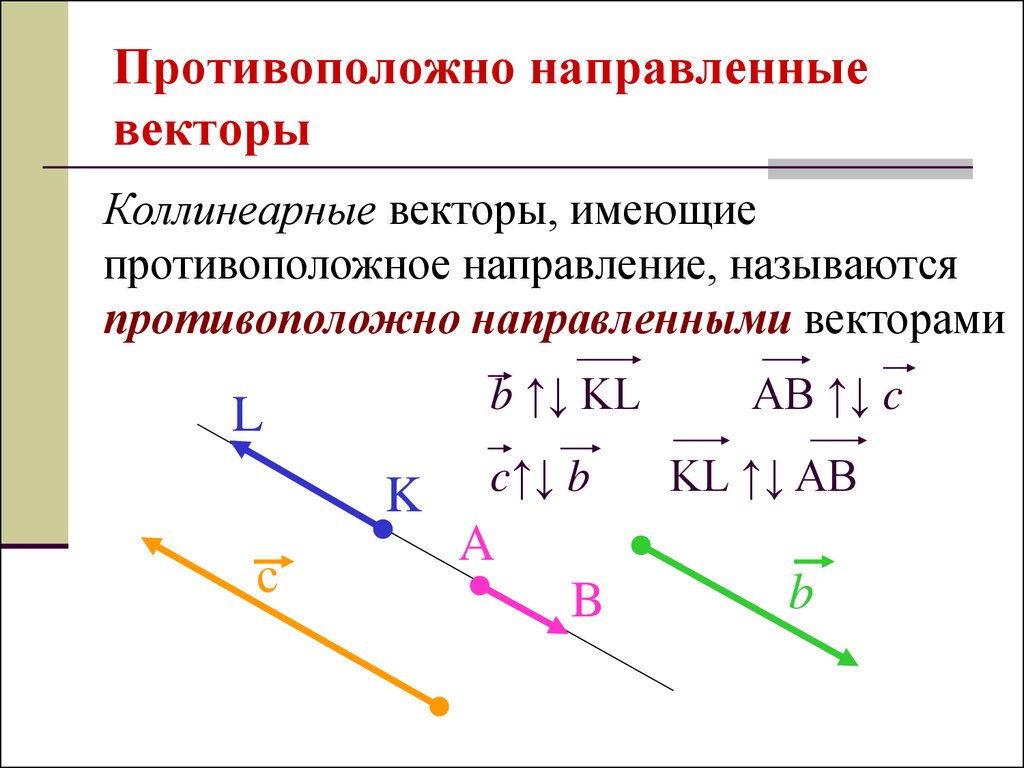
6. Противоположно направленные векторы

Коллинеарные векторы, имеющие
противоположное направление, называются
противоположно направленными векторами
b ↑↓ KL
L
K
с
c↑↓ b
AB ↑↓ c
KL ↑↓ AB
A
B
b

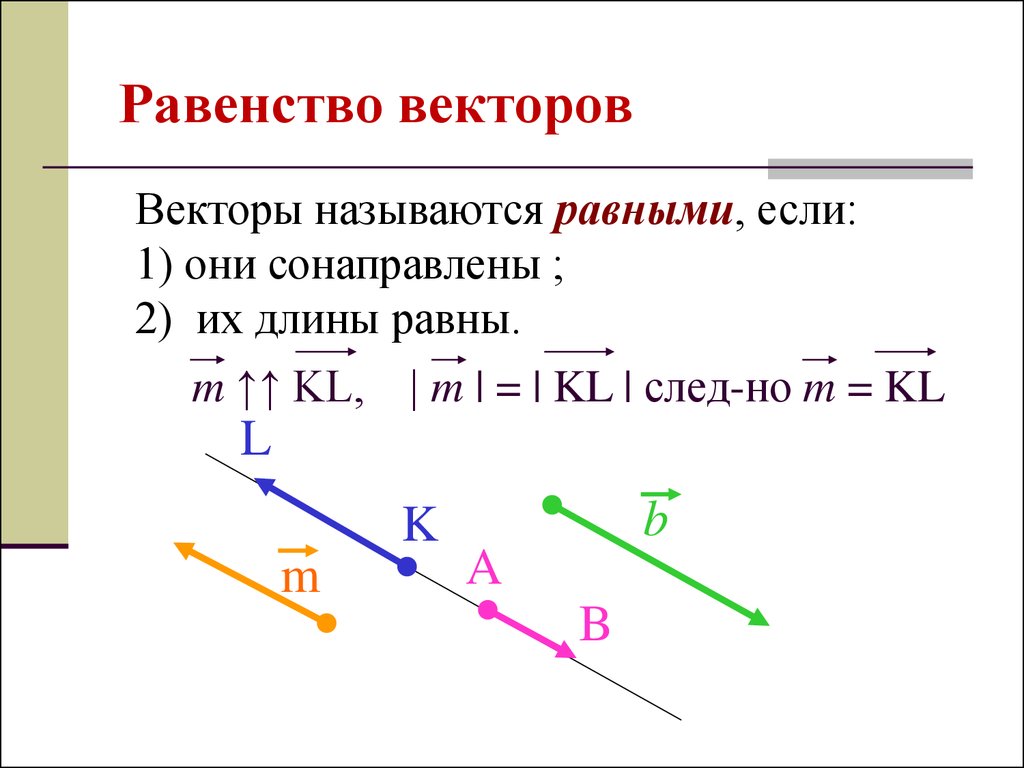
7. Равенство векторов

Векторы называются равными, если:
1) они сонаправлены ;
2) их длины равны.
m ↑↑ KL, | m | = | KL | след-но m = KL
L
K
m
b
A
B

8.

Векторы в пространстве
С1
D1
A1
ABCDA1 B1C1 D1 прямоуголь ный параллелепипед.
B1
AB 3, BC 4, CC1 5.
5
Назовите векторы, равные векторам
D
A
3
С
B
4
AB, BC , CC1 .
Назовите длины векторов :
AD, AA1 , AD1 , AC , BD1 .

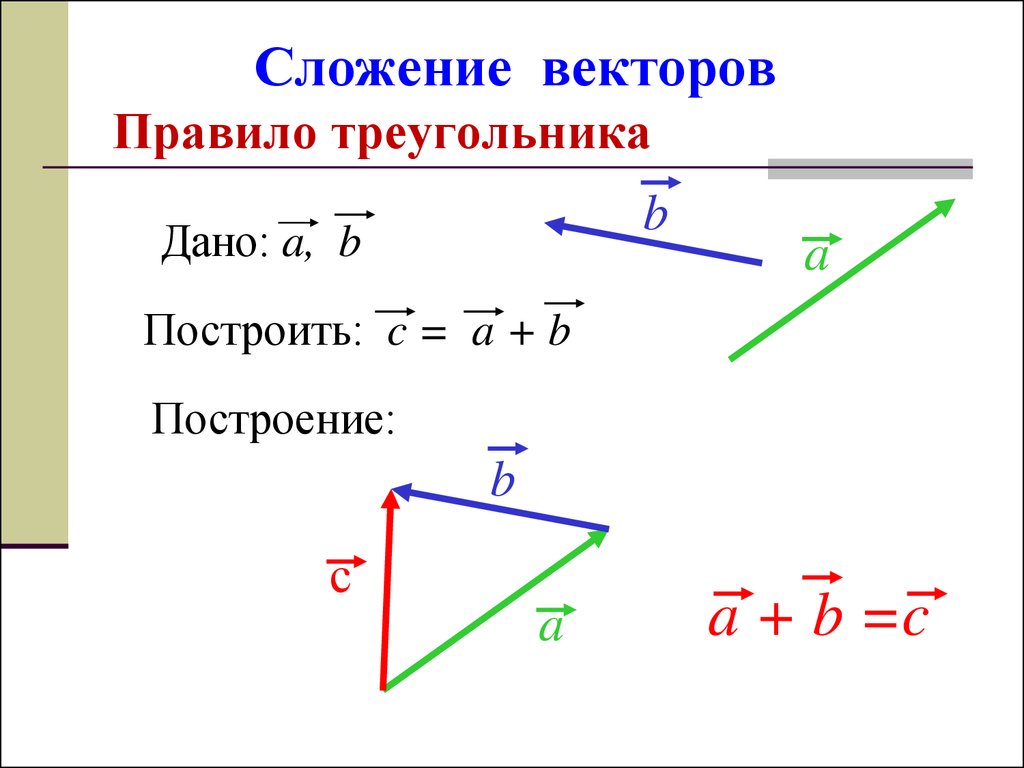
9. Сложение векторов Правило треугольника

b
Дано: a, b
a
Построить: c = a + b
Построение:
b
с
a
a + b =c

10. Сложение векторов Правило параллелограмма

b
Дано: a, b
a
Построить: c = a + b
Построение:
с
b
a
a + b =c

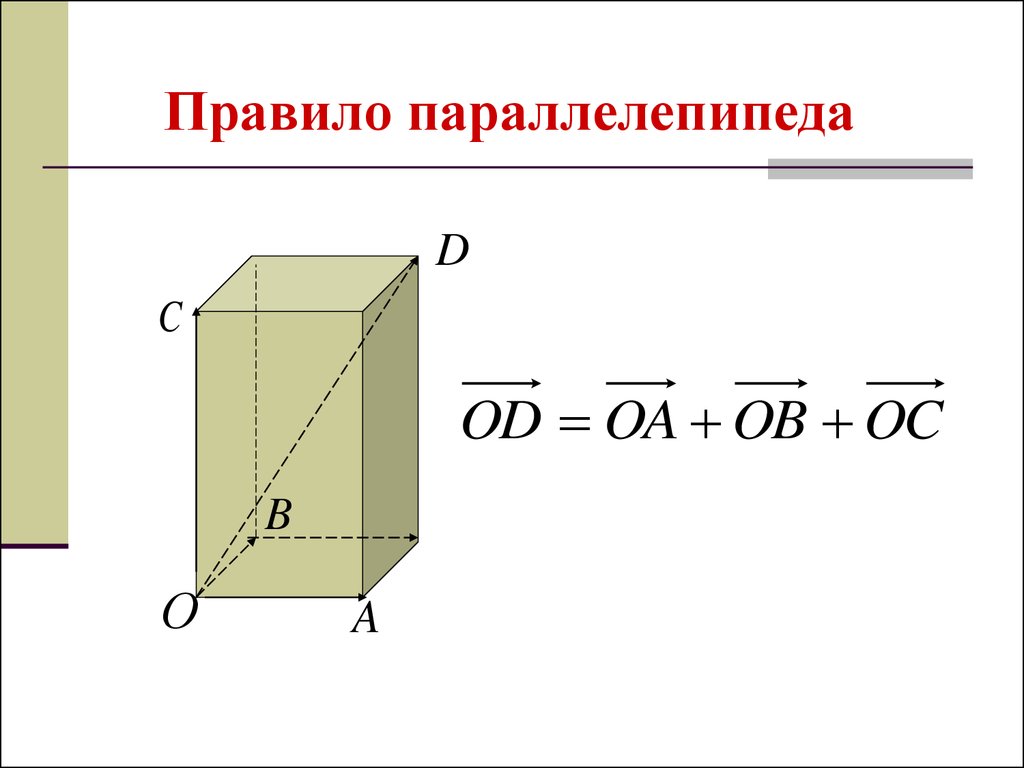
11.

Правило параллелепипеда
D
C
OD OA OB OC
B
О
A

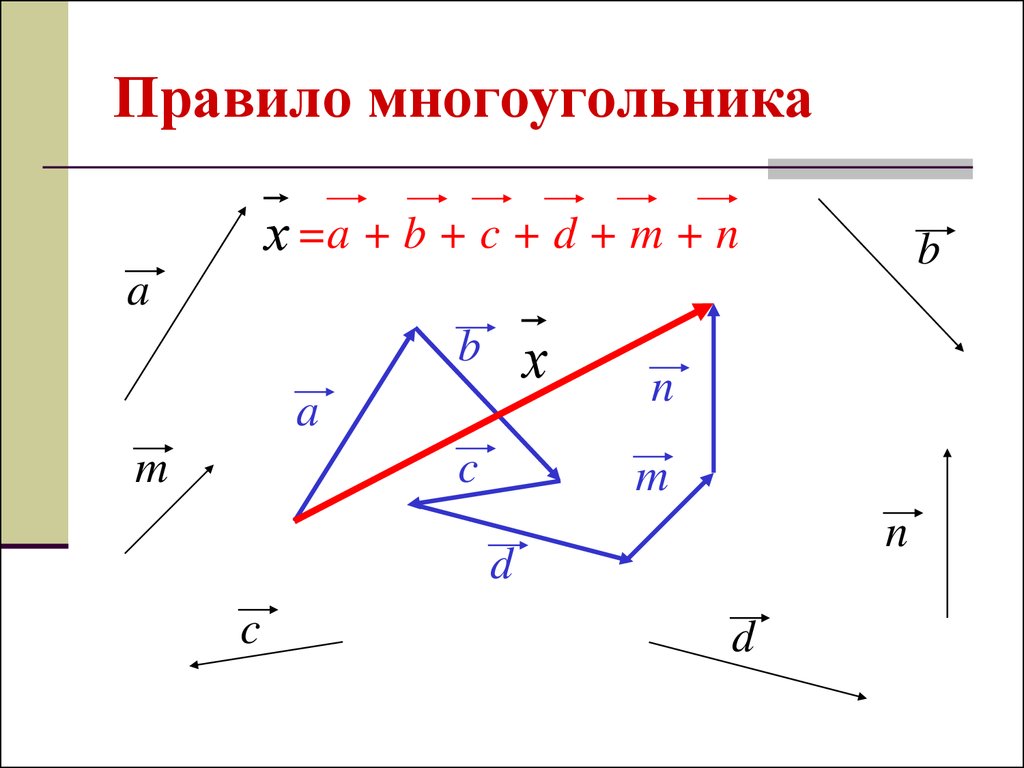
12. Правило многоугольника

х =a + b + c + d + m + n
b
a
х
b
a
m
c
n
m
n
d
c
d

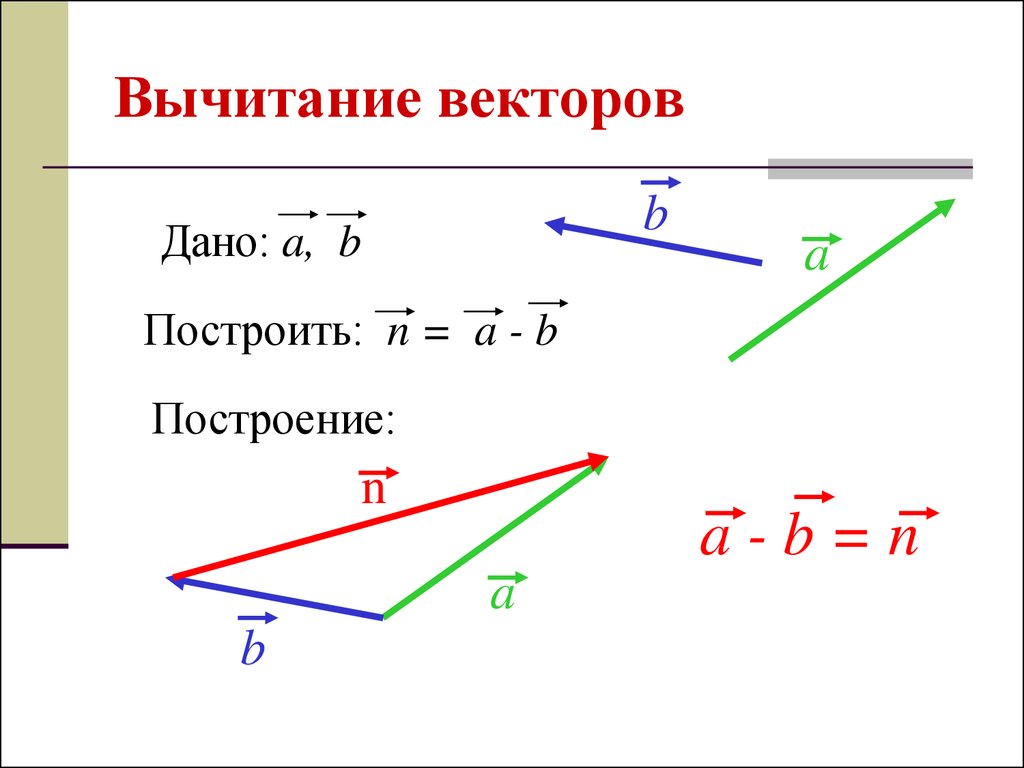
13. Вычитание векторов

b
Дано: a, b
a
Построить: n = a - b
Построение:
n
a-b=n
a
b

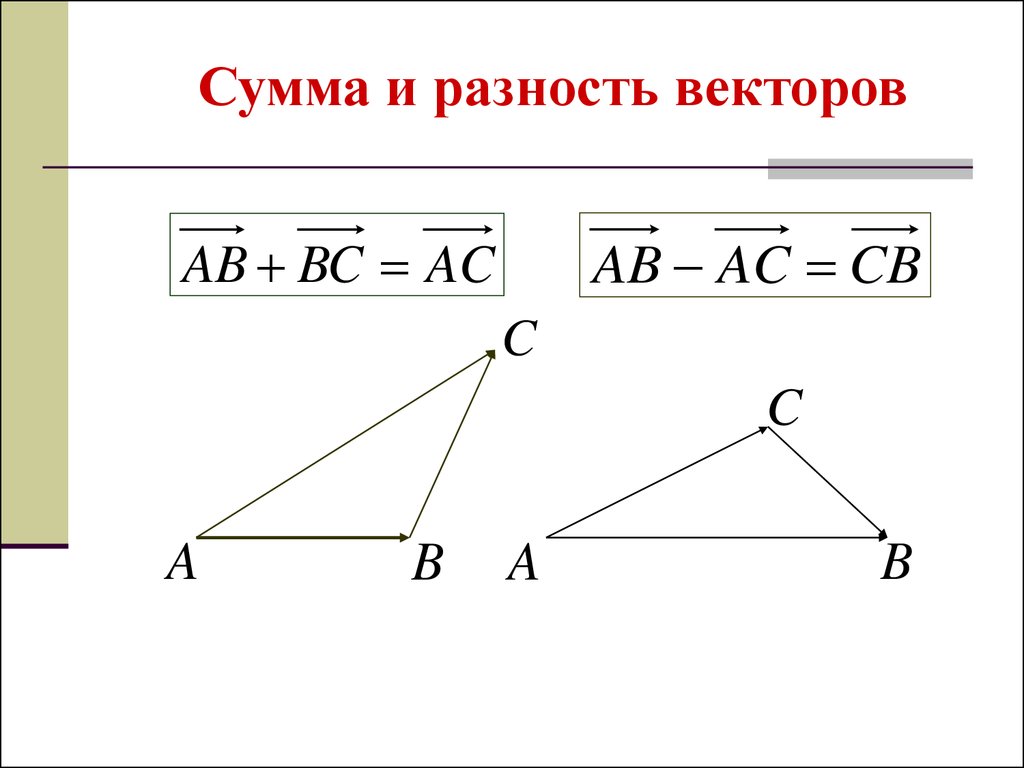
14.

Сумма и разность векторов
AB AC CB
AB BC AC
C
C
A
B
A
B

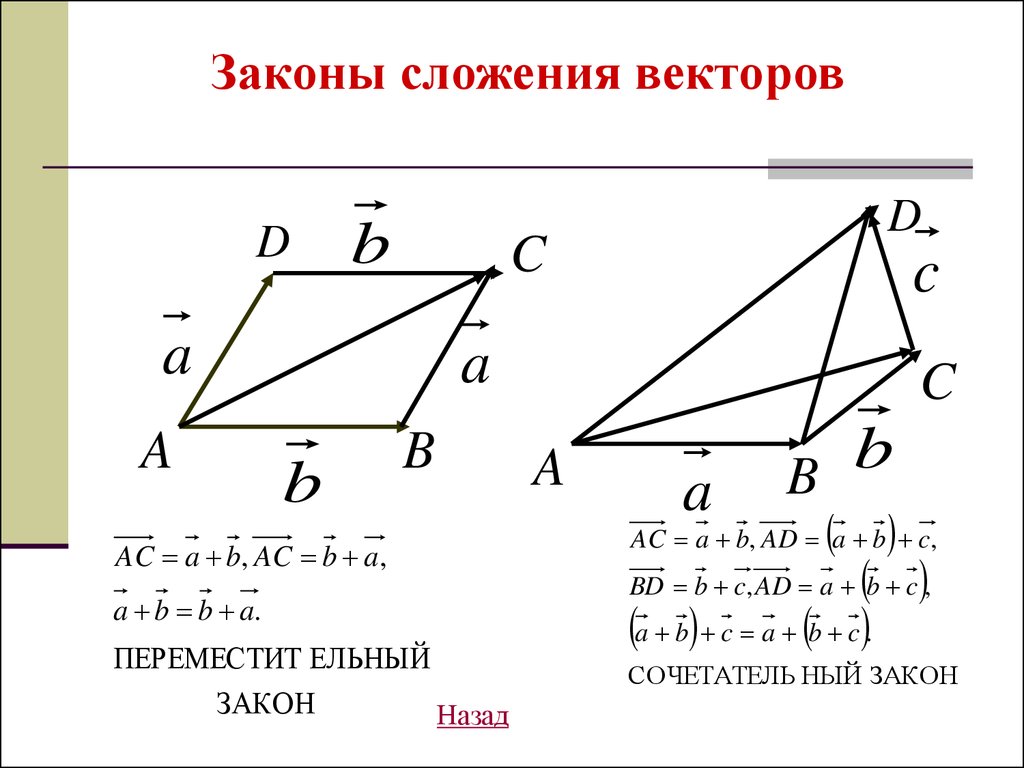
15.

Законы сложения векторов
D
b
D
C
a
c
a
A
b
B
A
a
b
B
AC a b, AD a b c,
AC a b, AC b a,
a b c a b c .
BD b c, AD a b c ,
a b b a.
ПЕРЕМЕСТИТ ЕЛЬНЫЙ
ЗАКОН
C
СОЧЕТАТЕЛЬ НЫЙ ЗАКОН
Назад

16. Умножение вектора a на число k

k·a = b,
|a| ≠ 0, k – произвольное число
|b| = |k|·|a|,
2a
если k> 0, то a ↑↑ b
a
если k< 0, то a ↑↓ b
-2a
Для любых чисел k, l и любых векторов a, b справедливы равенства:
1º. (kl)a= k(la) (сочетательный закон),
2º. (k+l)a= ka+la (первый распределительный закон),
3º. k(a+b) = ka+kb (второй распределительный закон).

17.

Умножение вектора на число
Сочетательный закон
kl a k l a
a
О
B
A
OA 3a , OB 6a ,
OB 2 OA 2 3a
6а 2 3а
2 3 a 2 3a

18.

Умножение вектора на число
Первый распределительный закон
k l a k a l a
a
О
OB 5a,
B
A
ОА 3а,
АВ 2а
ОВ OA АB
5а 3a 2а, тогда 3 2 a 3a 2a

19.

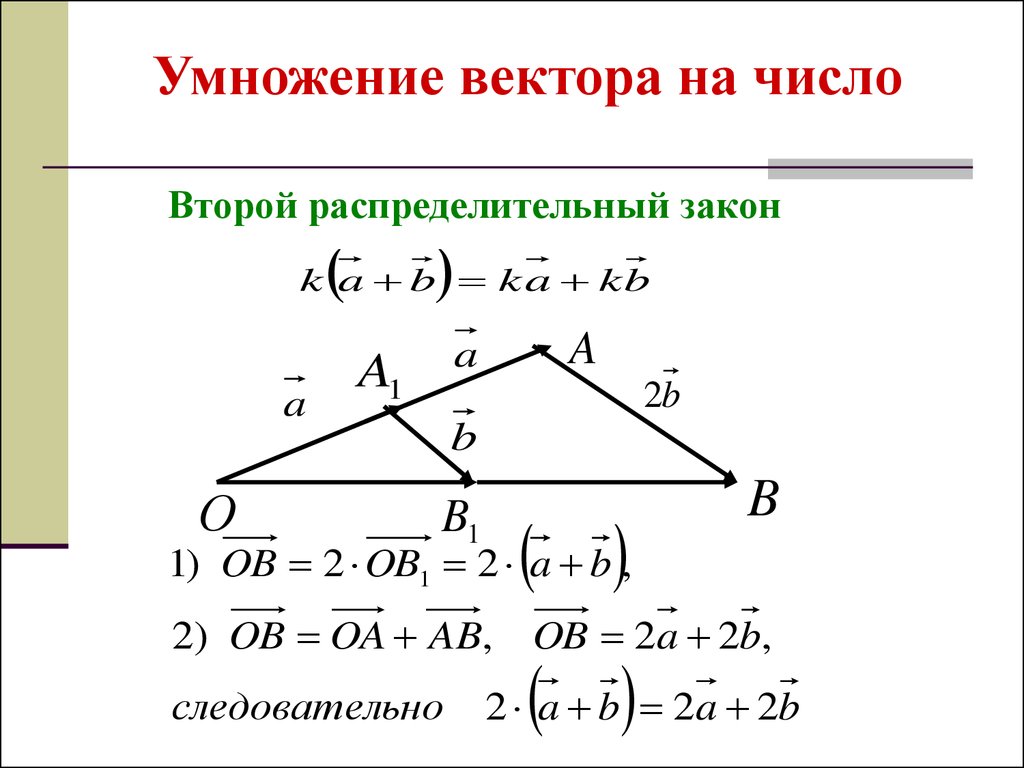
Умножение вектора на число
Второй распределительный закон
k a b k a kb
a
О
A
a
A1
2b
b
B1
B
1) OB 2 OB1 2 a b ,
2) OB OA AB, OB 2a 2b,
следовательно
2 a b 2a 2b

20.

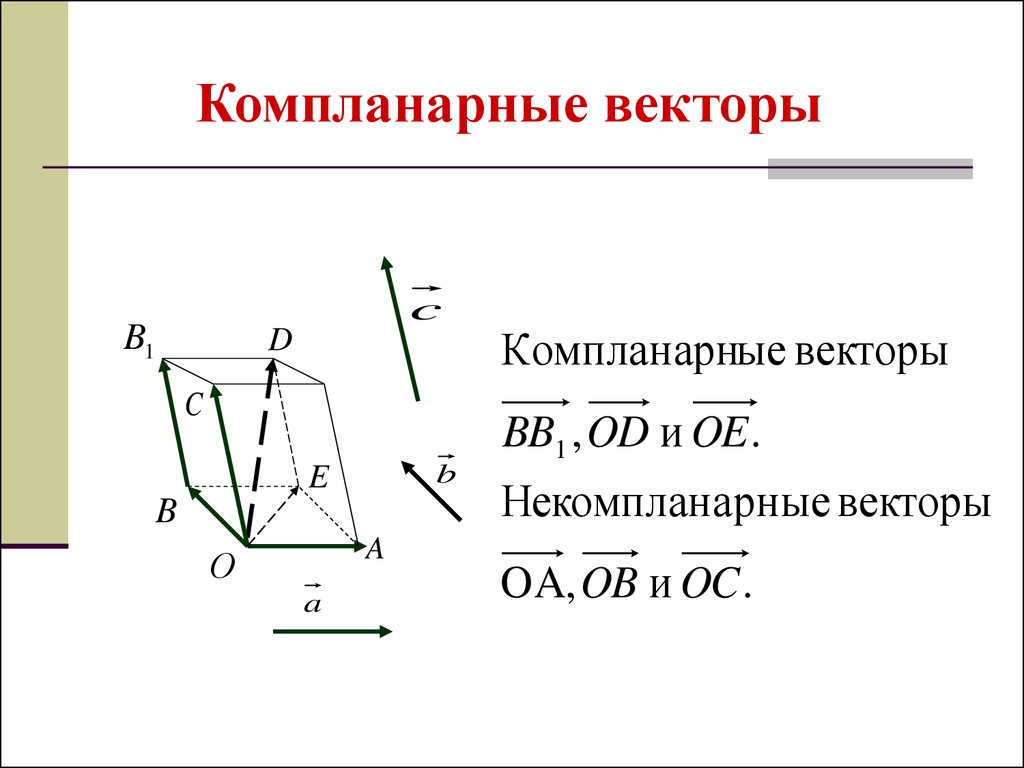
Компланарные векторы
Векторы называются компланарными,
если при откладывании их от одной точки они будут
лежать в одной плоскости.
Замечания
Если хотя бы один из трёх векторов — нулевой, то три
вектора считаются компланарными.
Тройка векторов, содержащая пару коллинеарных векторов,
компланарна.

21.

Компланарные векторы
c
B1
D
C
Компланарные векторы
BB1 , OD и OE .
b
E
B
A
О
a
Некомпланарные векторы
OA, OB и OC .

22. Прямоугольная система координат

Тройка взаимно
перпендикулярных
координатных прямых с
общим началом
координат.
Впервые введена
Р.Декартом(1596-1650)

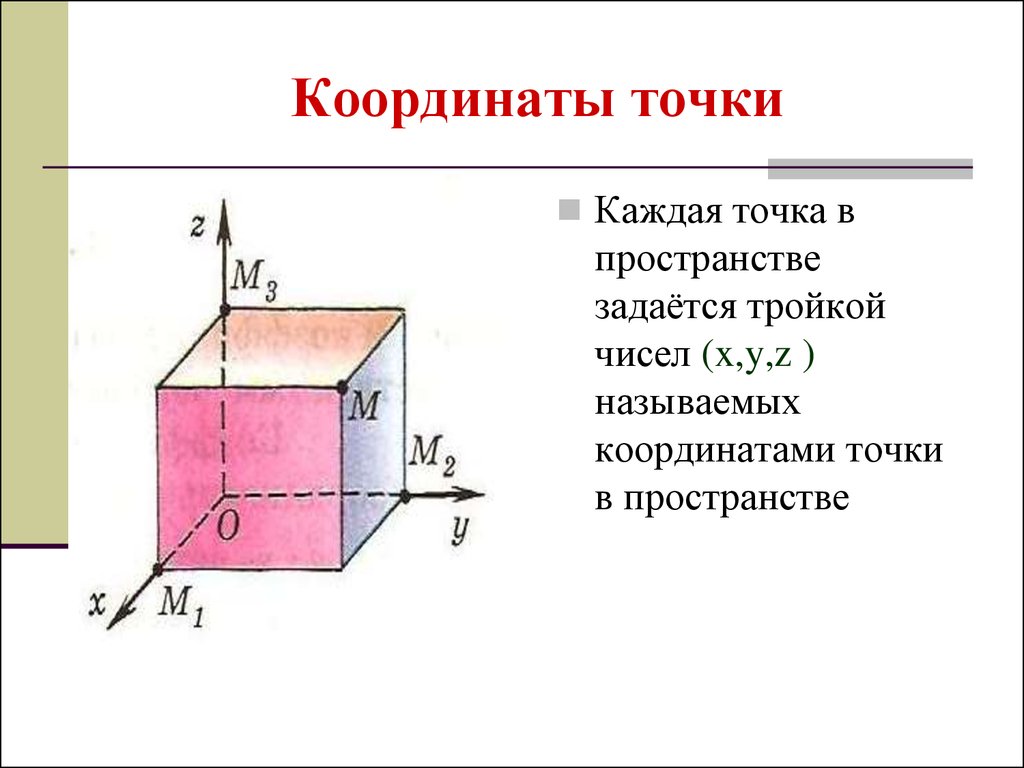
23. Координаты точки

Каждая точка в
пространстве
задаётся тройкой
чисел (x,y,z )
называемых
координатами точки
в пространстве

24. Координаты вектора

Векторы (i. j. k)
единичные векторы
Любой вектор можно
разложить по
координатным
векторам

25. Длина вектора

26. Скалярное произведение векторов

27. Свойства скалярного произведения. Угол между векторами.