Векторы в пространстве

1. Векторы в пространстве

вход

2. Содержание

I.
II.
III.
IV.
V.
VI.
Понятие вектора в пространстве
Коллинеарные векторы
Компланарные векторы
Действия с векторами
Разложение вектора
Базисные задачи
Проверь себя
Помощь в управлении презентацией
Выход

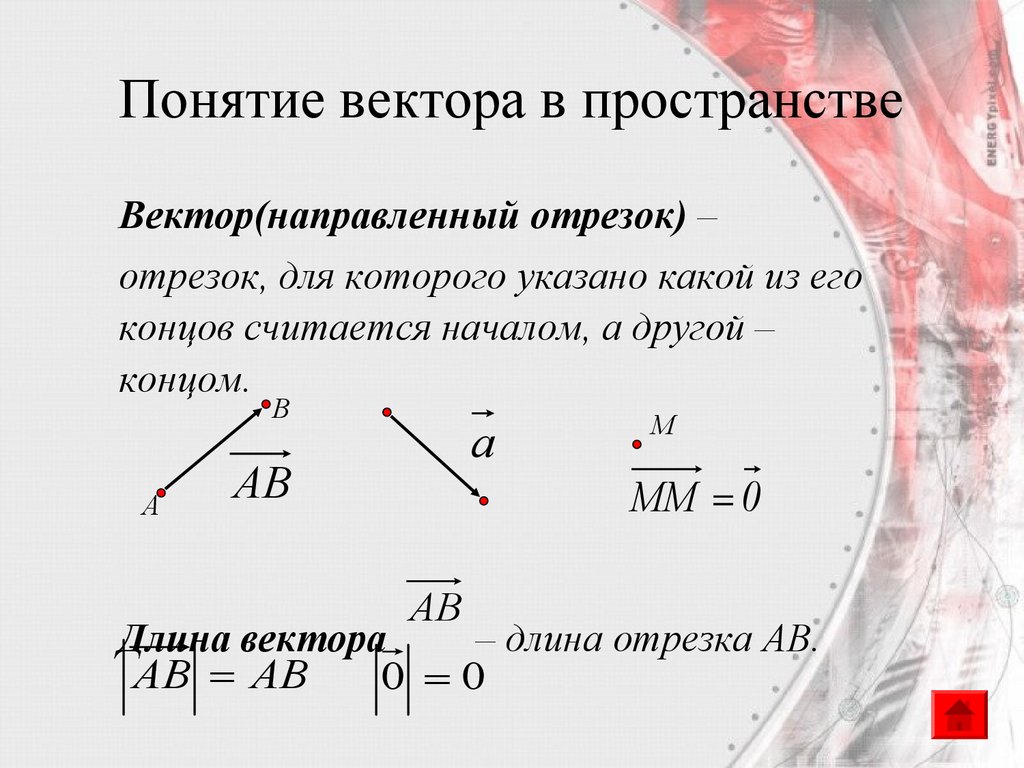
3. Понятие вектора в пространстве

Вектор(направленный отрезок) –
отрезок, для которого указано какой из его
концов считается началом, а другой –
концом.
В
А
a
AB
M
MM 0
AB
Длина вектора
– длина отрезка AB.
AB AB
0 0

4. Коллинеарные векторы

Два ненулевых вектора называются
коллинеарными, если они лежат на одной
прямой или параллельных прямых.
Среди коллинеарных различают:
• Сонаправленные векторы
• Противоположно направленные векторы

5. Сонаправленные векторы

Сонаправленные векторы - векторы, лежащие
по одну сторону от прямой, проходящей через их
начала.
a
a b
b
Нулевой вектор считается сонаправленным с
любым вектором.
• Равные векторы

6. Равные векторы

Равные векторы - сонаправленные векторы,
длины которых равны.
a
a b a b, a b
b
От любой точки можно отложить вектор,
равный данному, и притом только один.

7. Противоположно направленные векторы

Противоположно направленные векторы –
векторы, лежащие по разные стороны от прямой,
проходящей через их начала.
a
a b
b
Противоположные векторы

8. Противоположные векторы

Противоположные векторы – противоположно
направленные векторы, длины которых равны.
a
a b a b, a b
b
Вектором, противоположным нулевому,
считается нулевой вектор.

9. Признак коллинеарности

Если существует такое число k при котором
выполняетс я равенство a k b и при том
вектор b 0 , то векторы a и b коллинеарн ы.
Доказательство

10. Доказательство признака коллинеарности

Два вектора a и b коллинеарн ы тогда и
только тогда, когда имеет место равенство
a kb
вектор k a b, если k 0
( следует из определени я
вектор k a b, если k 0
произведен ия вектора на число )
Значит вектор b и k a коллинеарн ы,
т.к. сонаправленные и противолож но
направленные векторы лежат на одной
или параллельных прямых.
ч.т.д.

11. Определение компланарных векторов

Компланарные векторы – векторы, при
откладывании которых от одной и той же точки
пространства, они будут лежать в одной
плоскости.
Пример:
B1
A1
C1
D1
B
А
C
D
BB1 , AC,AC 1 компланарн ы, т.к.
BB1 AA1 , а векторы AA1 , AC , AC1
лежат в плоскости (AA1C)

12. О компланарных векторах

Любые два вектора всегда компланарны.
α
a
b
a
a
b
b
a и b компланарн ы
Три вектора, среди которых имеются два
коллинеарных, компланарны.
a, b и c
компланарн ы
если
a, b, c
a kb

13. Признак компланарности

Если вектор c можно разложить по векторам
а и b, т.е. представить в виде
с xa yb
где х и у некоторые числа, то векторы a, b
и c компланарн ы.
Доказательство
Задачи

14. Задачи на компланарность

1)
2)
Компланарны ли векторы:
а) a, b, 2a, 3b;
б) a, b, a b, a b ?
Справка
Решение
Известно, что векторы a , b и c компланарны.
Компланарны ли векторы:
а) a, 2b, 3c;
б) a b, a 2c, 2b 3c ?
Справка
Решение

15. Решение

а )векторы a и 2a коллинеарн ы,
векторы b и 3b коллинеарн ы,
значит векторы a, b, 2a и 3b компланарн ы
б )векторы a, b и a b компланарн ы,
векторы a, b и a b компланарн ы,
значит векторы a, b, a b и a b компланарн ы

16. Решение

a) если векторы a , 2b , 3c компланарн ы,
то существуют такие х и у, что
a xb y c
проверяем существуют ли такие т и п,что
a m 2b n 3c
имеем :
x
2m x m
2
y
3n y n
3
m и п определяют ся единственн ым образом,
значит векторы компланарн ы

17. Решение

б)если векторы a b , a 2c , 2b 3c
компланарн ы, то существуют такие х и у, что
a b x( a 2c ) y(2b 3c )
a b x a 2xc 2yb 3y c
a(1 x) b(1 2y) c( 2x 3y) 0
1 x 0 x 1
1
1 2y 0
y
3y 2x 0
2
1
a b a 2c (2b 3c )
2
искомые х и у существуют,
значит векторы компланарн ы

18. Доказательство признака компланарности

B1 OC x OA y OB
С
с x a yb
c
B
b
x, y некоторые числа
A
Доказать :
A1
O
Дано :
a
a, b и с компланарн ы
Доказатель ство :
Пусть a и b не коллинеарн ы
О произвольн ая точка
OA a , OB b
OA,OB ,OA1 ,OB1 (OAB)
OA1 x OA OB1 y OB
OC c OA1 OB1 x OA y OB
OA a ,OB b ,OC c лежат в одной плоскости
a ,b , c компланарн ы ч.т.д

19. Свойство компланарных векторов

Если векторы a, b и c компланарн ы, то один из них
можно выразить линейным образом через два других,
т.е. представить в виде :
с xa yb
причем коэффициен ты разложения
определяются единственным образом .

20. Действия с векторами

Сложение
Вычитание
Умножение вектора на число
Скалярное произведение

21. Сложение векторов

•Правило треугольника
•Правило параллелограмма
•Правило многоугольника
•Правило параллелепипеда
•Свойства сложения

22. Правило треугольника

Для сложения двух векторов необходимо :
1. отложить от какой нибудь точки А вектор
AB , равный а
2. от точки В отложить вектор BC , равный b
3. вектор AC называется суммой векторов a и b
B
a
a
b
А
b
a b
C

23. Правило треугольника

B
a
А
b
a b
C
Для любых трех точек А, В и С справедливо равенство:
AB BC AC

24. Правило параллелограмма

Для сложения двух векторов необходимо :
1. отложить от какой нибудь точки А
вектор AB, равный а
2. от точки А отложить вектор AC , равный b
3. достроить фигуру до параллелог рамма , проведя
дополнител ьные линии параллельн о данным
векторам
4. диагональ параллелограмма сумма векторов
B
a
a
b
А
с
b C
с a b

25. Свойства сложения

Для любых векторов a , b и c справедлив ы
равенства :
a b b a
переместит ельный закон
a b с а b с сочетатель ный закон

26. Правило многоугольника

Сумма векторов равна вектору, проведенному
из начала первого в конец последнего(при
последовательном откладывании).
a
B
b
C
A
e
E
c
d
a b c d e
Пример
D
AB BC C D DE AE

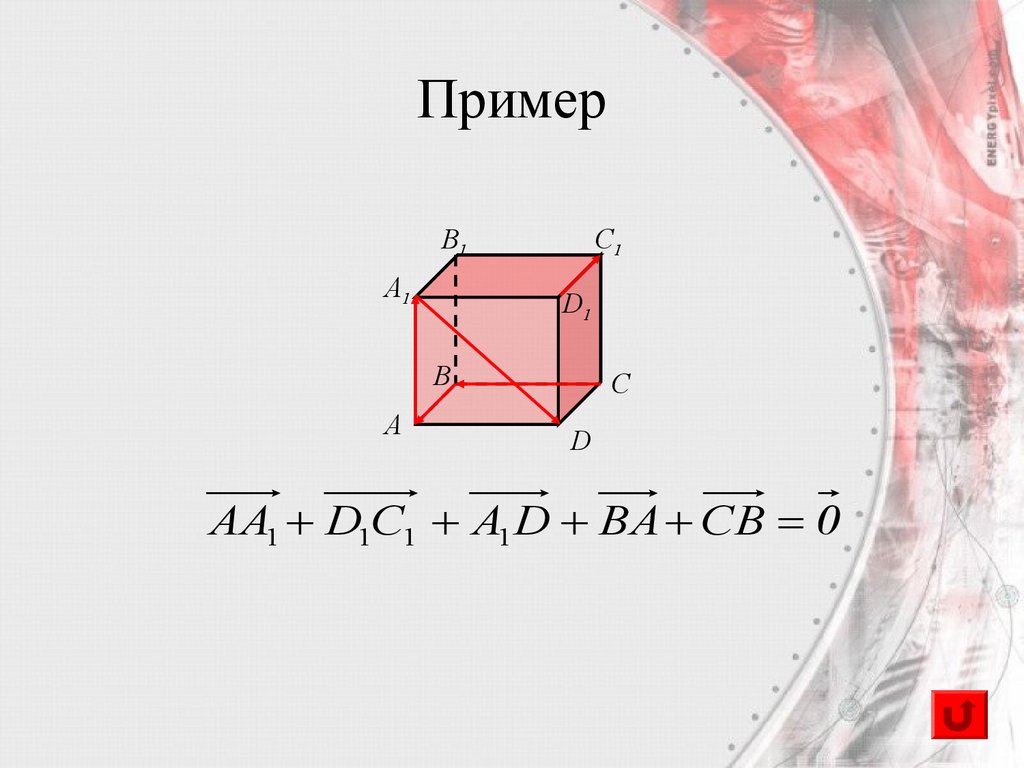
27. Пример

B1
A1
C1
D1
B
A
C
D
AA1 D1C1 A1 D BA CB 0

28. Правило параллелепипеда

Вектор, лежащий на диагонали параллелепипеда,
равен сумме векторов, проведенных из той же
точки и лежащих на трех измерениях
параллелепипеда.
B1
A1
с bB
А
C1
d
AB b
D1
C
a
AD a
D
AC1 AD AB AA1
AA1 c
AC1 d

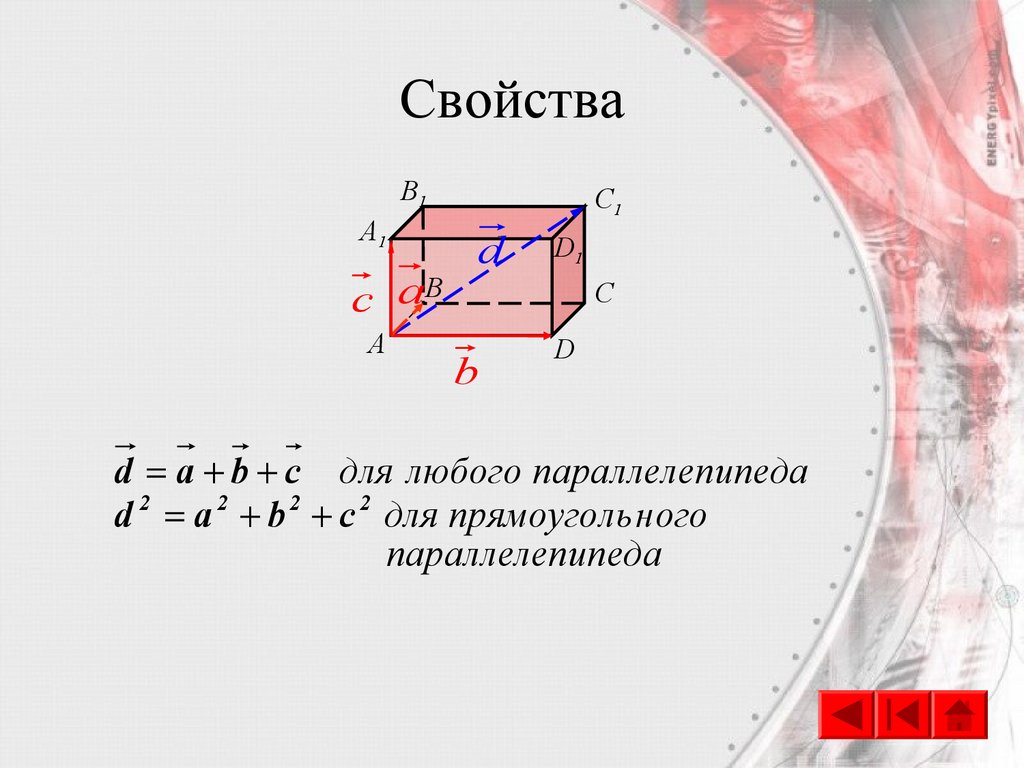
29. Свойства

B1
A1
с aB
А
C1
d
D1
C
b
D
d a b c для любого параллелепипеда
d 2 a 2 b 2 c 2 для прямоуголь ного
параллелепипеда

30. Вычитание векторов

• Вычитание
• Сложение с противоположным

31. Вычитание

Разностью векторов
и
называется
a b такой
вектор, сумма которого с вектором
вектору
.
a
равна
b

32. Вычитание

Для вычитания одного вектора из другого необходимо :
1. отложить от какой нибудь точки А
вектор AB, равный а
2. от этой же точки А отложить вектор AC ,
равный b
3. вектор CB называется разностью векторов a и b
a
B
b
Правило трех точек
a
a b
A
b
C

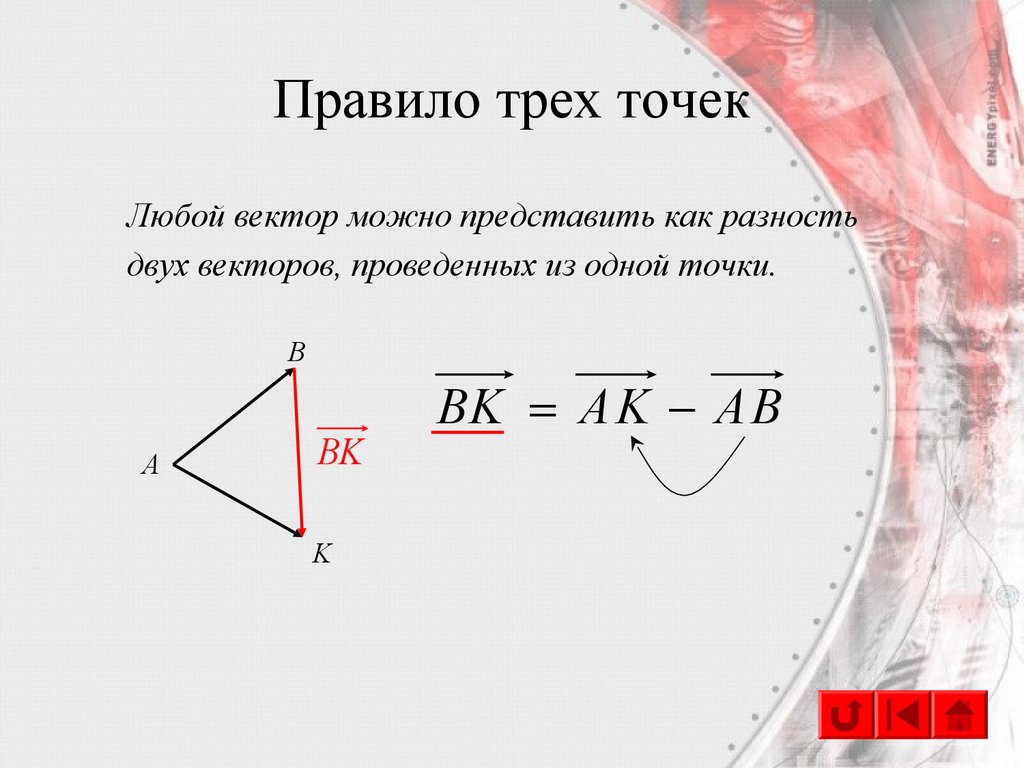
33. Правило трех точек

Любой вектор можно представить как разность
двух векторов, проведенных из одной точки.
B
А
BK
K
BK AK AB

34. Сложение с противоположным

Разность векторов a и b можно представить
как сумму вектора a и вектора,
противоположного вектору b.
a b a b
a
B
b
a b
b
O
А
a

35. Умножение вектора на число

Произведением ненулевого вектора a на число k
называется такой вектор b , длина которого
равна к а , при чем векторы a и b сонаправлены
при k 0 и противоположно направлены при k 0.
a
2a
b
1
b
3

36. Свойства

•Произведением нулевого вектора на любое число
считается нулевой вектор.
0 n 0
•Произведение любого вектора на число нуль есть
нулевой вектор.
n 0 0

37. Свойства

Для любых векторов a и b и любых
чисел k, l справедливы равенства :
(kl)a k(l a )
сочетатель ный закон
k( a b ) k a k b
1 ый распределительный
закон
(k l)a k a l a
2 ой распределительный
закон

38. Скалярное произведение

Скалярным произведением двух векторов
называется произведение их длин на косинус угла
между ними.
a b a b cos( a ; b )
Справедливые утверждения
Вычисление скалярного произведения в координатах
Свойства скалярного произведения

39. Справедливые утверждения

• скалярное произведение ненулевых векторов
равно нулю тогда и только тогда, когда эти
векторы перпендикулярны
a b 0 a 0 b 0 a b
• скалярный квадрат вектора (т.е. скалярное
произведение вектора на себя) равен квадрату
его длины
a
2
а
2
а
2

40. Вычисление скалярного произведения в координатах

Скалярное произведен ие векторов a x1 ; y1 ; z1
и b x 2 ; y 2 ; z 2 выражается формулой
a b x 1 x 2 y1 y 2 z 1 z 2
Доказательство