Векторы в пространстве

1.

2.

Коллинеарные
векторы
Абсолютная
величина
(длина вектора)
Обозначение
векторов
Нулевой
вектор
Действия
над
векторами
Компланарные
векторы
История
возникновения
вектора
Правило треугольника
Вычитание векторов
Правило
параллелограмма
Правило
Многоугольника
Понятие
вектора
Равенство
векторов

3.

Понятие вектора появилось в
XIX веке в работах
Герман Гюнтер Грассман 1809
—1877.
Уильям Роуан Гамильтон
4.08.1806 — 02.09.1865

4.

1845 году - ирландский
математик и астроном
Уильям Гамильтон
ввел понятие вектора
Почти одновременно…
исследования с другой
точки зрения немецким
математиком
Герман Грассман
Англичанин Уильям Клиффорд
сумел объединить два подхода в рамках общей теории
Окончательный вид - в трудах американского физика и
математика Джозайи Уилларда Гиббса ,
который в 1901 году опубликовал обширный учебник
по векторному анализу.

5.

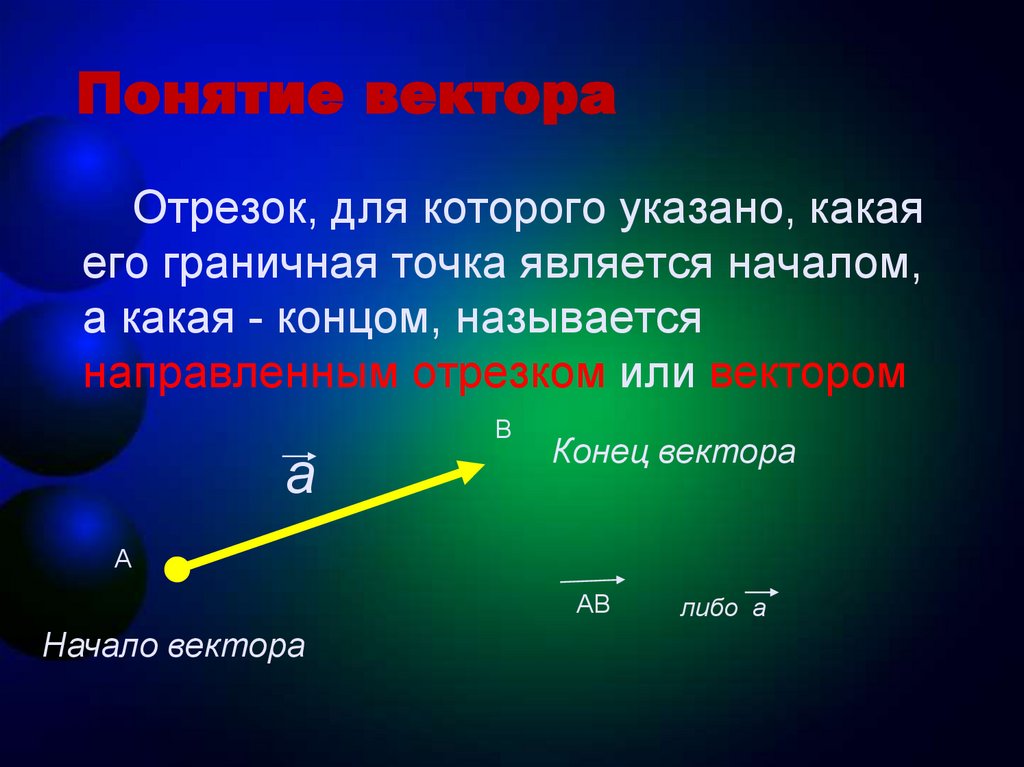
Понятие вектора
Отрезок, для которого указано, какая
его граничная точка является началом,
а какая - концом, называется
направленным отрезком или вектором
B
a
Конец вектора
A
AB
Начало вектора
либо а

6.

Длина вектора
Е
К
Длиной вектора или
модулем (абсолютной
величиной) ненулевого
вектора называется длина
отрезка
|КЕ| = |KE| длина вектора
М
КЕ
вектор ММ - нулевой вектор
|ММ| = 0

7.

Коллинеарные векторы
Ненулевые векторы называются
коллинеарными, если они лежат на
одной прямой или на параллельных
прямых
L
с
K
b
A
B
М
Нулевой вектор считается
коллинеарным любому вектору

8. Сонаправленные векторы

Коллинеарные векторы, имеющие
одинаковое направление,
называются сонаправленными
векторами
c ↑↑ KL
AB ↑↑ b
MM ↑↑ (любому
вектору)
L
с
b
K
A
М
B

9. Противоположно направленные векторы

Коллинеарные векторы, имеющие
противоположное направление,
называются противоположно
направленными векторами
L
b ↑↓ KL
AB ↑↓ c
c↑↓ b
K
KL ↑↓ AB
A
с
B
b

10.

Равенство векторов
Векторы называются равными, если:
1) они сонаправлены ;
2) их длины равны.
m ↑↑ KL, | m | = | KL | след-но m =
KLL
b
K
m
A
B

11.

Сложение векторов
Правило треугольника
b
Дано: a, b
a
Построить: c = a + b
Построение:
b
с
a
a + b =c

12. Сложение векторов Правило параллелограмма

b
Дано: a, b
a
Построить: c = a + b
Построение:
с
a
b
a + b =c

13.

Правило многоугольника
х =a + b + c + d + m + n
b
a
х
b
a
m
c
n
m
n
d
c
d

14.

Задача: мышки и сыр
a
b
c
d
e
i
f
g
a i 0
b g 0
c h 0
h
m
e
f
d
e f d m

15.

16.

Вычитание векторов
b
Дано: a, b
a
Построить: n = a - b
Построение:
n
a
b
a-b=n

17.

Правило параллелепипеда
D
C
OD OA OB OC
B
О
A

18.

Правило параллелепипеда
D
C
OD OA OB OC
B
О
A

19.

Компланарные векторы
Векторы называются компланарными,
если при откладывании их от одной точки они будут
лежать в одной плоскости.
Замечания
Если хотя бы один из трёх векторов — нулевой, то три
вектора считаются компланарными.
Тройка векторов, содержащая
пару коллинеарных векторов, компланарна.

20.

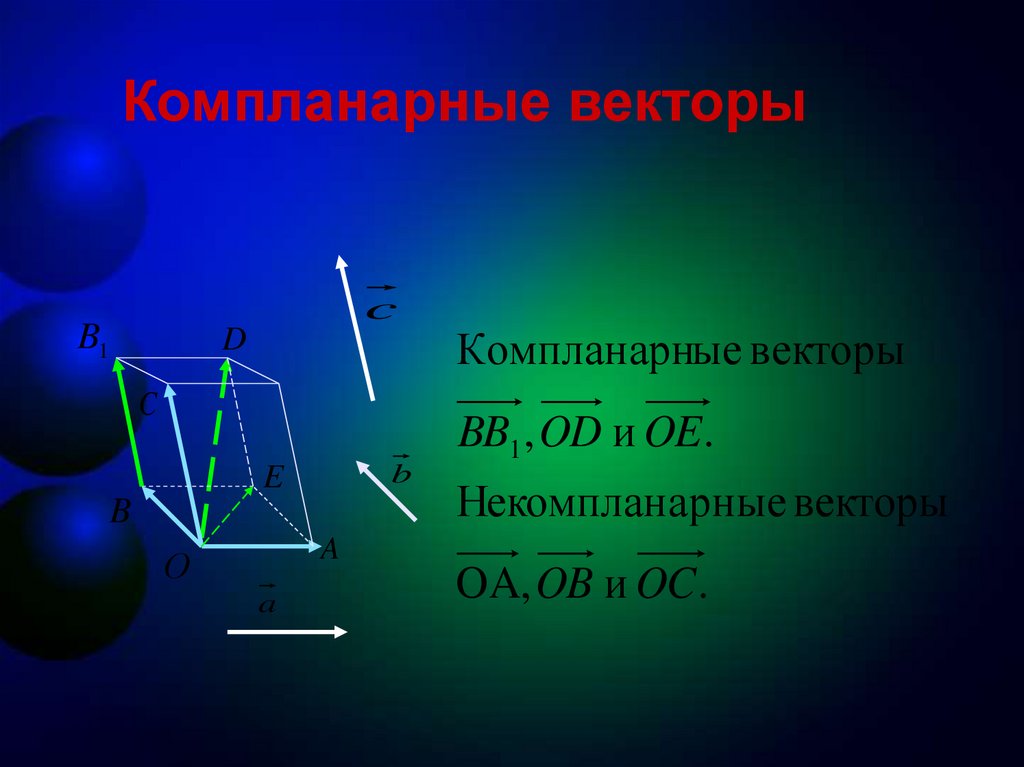
Компланарные векторы
c
B1
D
C
Компланарные векторы
BB1 , OD и OE .
b
E
B
A
О
a
Некомпланарные векторы
OA, OB и OC .

21.

F1 F1 F 4 0
F 2 F3 m
F3
F2
F4
m

22.

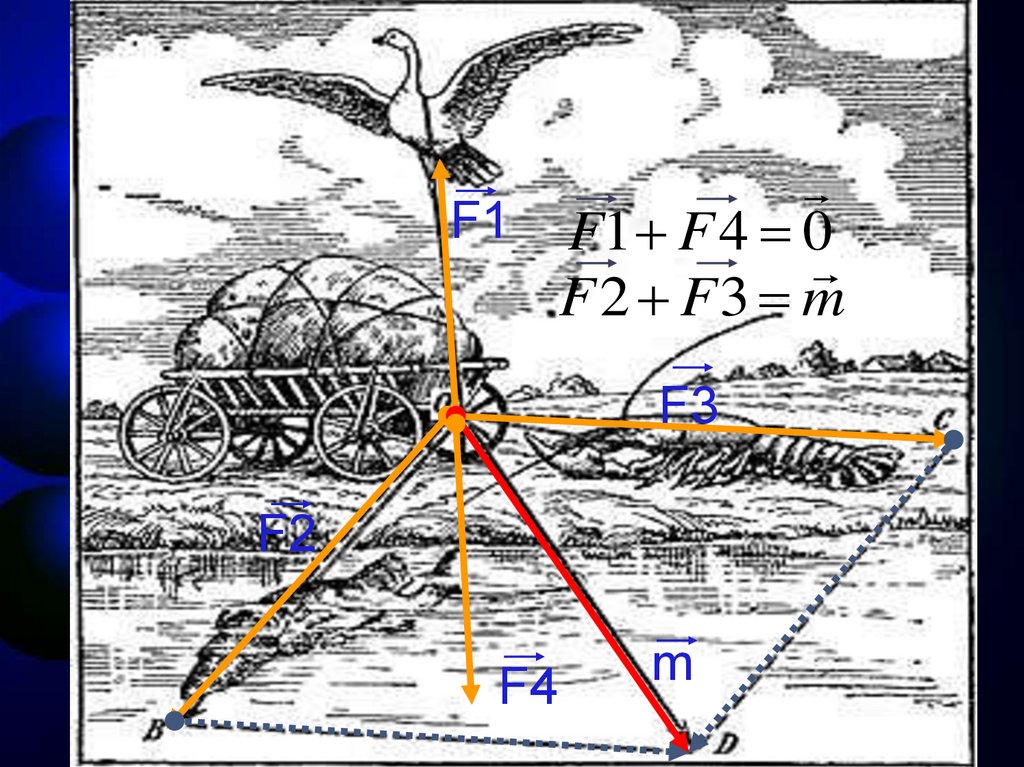
Задача о лебеде, раке и щуке,
решенная по правилам механики.
F1 - тяга лебедя, направлена вверх (, уменьшает трение колес о
землю и об оси, облегчая тем вес воза, а может быть, даже
вполне уравновешивая его, – ведь груз невелик («поклажа бы для
них казалась и легка»)
F2 - тяга щуки (ОВ), – вбок;
F3 - тяга рака (ОС), – назад;
F4 - вес воза, которая направлена отвесно вниз.
В какую сторону сдвинется воз: вперед, назад или вбок?
Это зависит уже от соотношения сил и от величины угла между ними.
При одном только условии воз может не сдвинуться
под действием этих трех сил:
если трение у его осей и о полотно дороги больше, чем
приложенные усилия. Но это не согласуется с утверждением,
что «поклажа бы для них казалась и легка».

23.

ТВОРЧЕСКАЯ ЗАДАЧА:
ИЗОБРАЗИТЬ НАПРАВЛЕНИЯ ДЕЙСТВИЯ
СИЛ ТЯГ ГЕРОЕВ БАСНИ
И РЕЗУЛЬТИРУЮЩИЙ ВЕКТОР ЭТИХ СИЛ