Вектори на площині

1. Вектори на площині

ВЕКТОРИ НА ПЛОЩИНІ
1

2. План

ПЛАН
1.Поняття вектора. Історична довідка.
2.Вектор. Модуль і напрям вектора. Рівність
векторів.
3.Координати вектора.
4.Додавання векторів.
5.Віднімання векторів.
6.Множення вектора на число. Колінеарні
вектори.
7.Скалярний добуток векторів.
2

3. Поняття вектора

ПОНЯТТЯ ВЕКТОРА
Поняття вектора є одним із фундаментальних понять сучасної
математики. Його можна визначати по-різному:
Як напрямлений
відрізок
Як упорядковану пару
точок, що є кінцями
напрямленого
відрізка
Як паралельне
перенесення
3

4. Поняття вектора

ПОНЯТТЯ ВЕКТОРА
Г. Грассман
В. Гамільтон
Поняття вектора уперше з’явилось в роботах
німецького математика XIX ст. Г. Грассмана і
ірландського математика В.Гамільтона. Потім воно було
охоче сприйняте багатьма математиками і фізиками.
В сучасній математиці це поняття відіграє дуже
важливу роль.
4

5. Застосування вектора

ЗАСТОСУВАННЯ ВЕКТОРА
Уперше поняття вектора як напрямленого
відрізка знайшло застосування в механіці для
зображення фізичних векторних величин:
швидкості, прискорення, сили, моменту сили
тощо.
Високий ступінь наочності і простота геометричних
операцій над векторами як напрямленими відрізками
сприяли тому, що поняття вектора знайшло загальне
визнання і застосування в інших розділах фізики: в
кінематиці, статиці, динаміці точки і динаміці системи,в
теорії відносності, в теорії потенціалу та гідродинаміці.
Також стало одним із основних понять таких наук, як
векторна алгебра, векторний аналіз, теорія поля.
5

6. Математичне поняття вектора

МАТЕМАТИЧНЕ ПОНЯТТЯ ВЕКТОРА
Проте хоча поняття вектора знайшло перше
застосування в фізиці, це математичне поняття, усі операції
над якими виконуються за законами математики.
Вектор як математичне поняття міцно ввійшов у
шкільну математику, у різні нематематичні науки. В школі
за допомогою векторного методу розв’язується багато
різноманітних задач, які не мають іншого способу
розв’язання.
Саме тому вивчення поняття вектора є дуже важливим
в сучасних умовах розвитку математичних наук.
6

7. Вектор. Позначення вектора

ВЕКТОР. ПОЗНАЧЕННЯ ВЕКТОРА
Вектором називається
напрямлений відрізок,
тобто відрізок в якому
виділено початок і кінець
Вектори позначають так:
а, b, c
Або за початком і кінцем:
AB, CD.
7

8. Модуль вектора

МОДУЛЬ ВЕКТОРА
Абсолютною величиною
(або модулем) називається
довжина відрізка, що
задає вектор.
Абсолютна величина нульвектора дорівнює нулю.
а
| a | AB
| 0 | 0
8

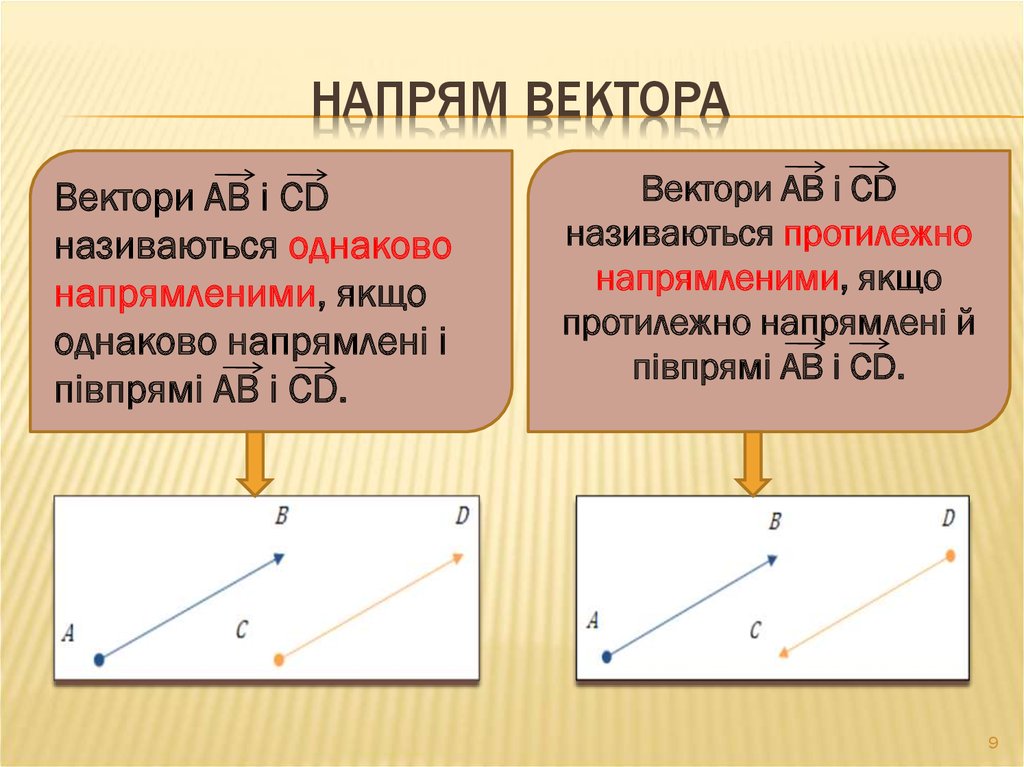
9. Напрям вектора

НАПРЯМ ВЕКТОРА
Вектори АВ і CD
називаються однаково
напрямленими, якщо
однаково напрямлені і
півпрямі АВ і СD.
Вектори АВ і СD
називаються протилежно
напрямленими, якщо
протилежно напрямлені й
півпрямі АВ і СD.
9

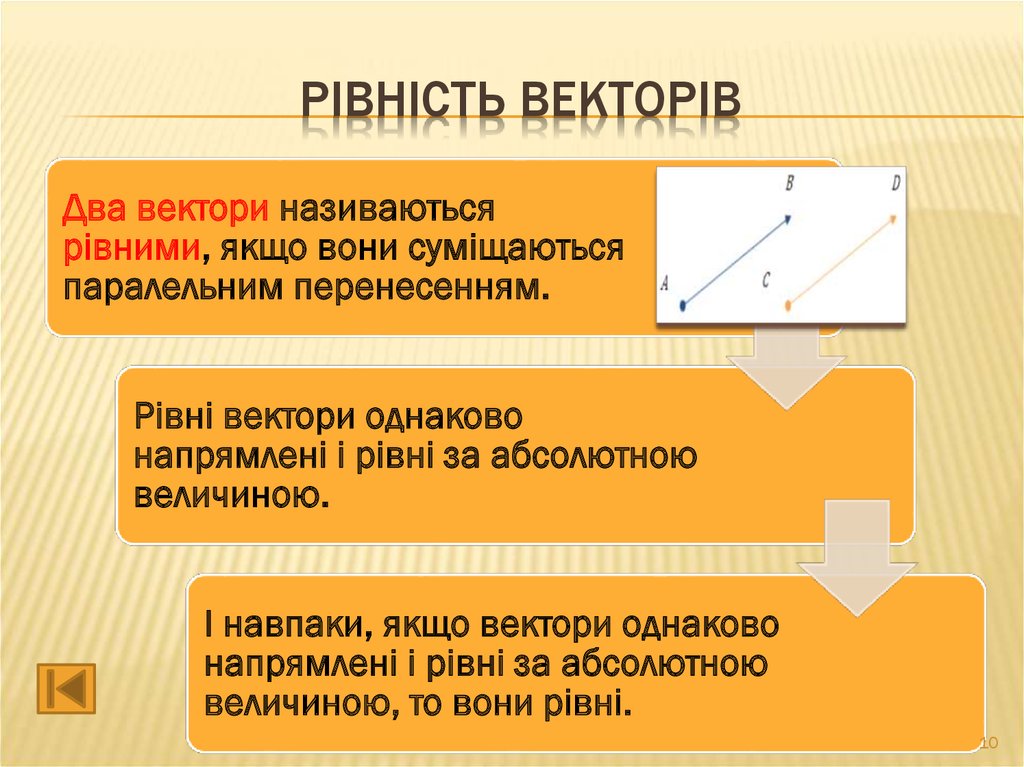
10. Рівність векторів

РІВНІСТЬ ВЕКТОРІВ
Два вектори називаються
рівними, якщо вони суміщаються
паралельним перенесенням.
Рівні вектори однаково
напрямлені і рівні за абсолютною
величиною.
І навпаки, якщо вектори однаково
напрямлені і рівні за абсолютною
величиною, то вони рівні.
10

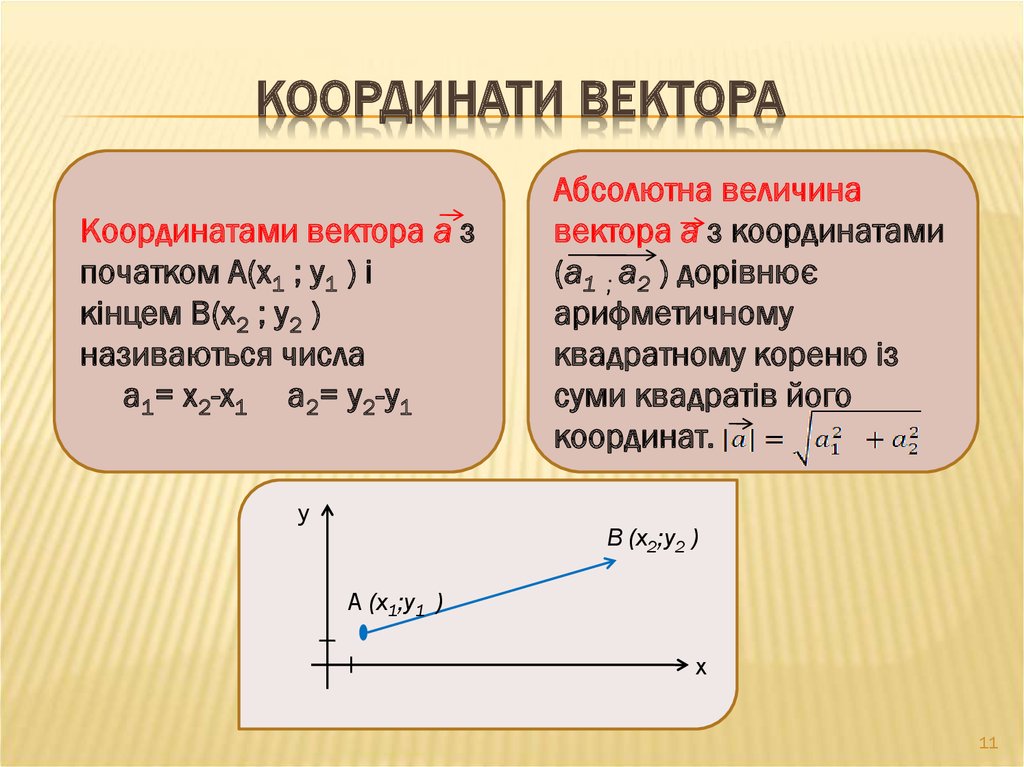
11. Координати вектора

КООРДИНАТИ ВЕКТОРА
Координатами вектора а з
початком А(х1 ; у1 ) і
кінцем В(х2 ; у2 )
називаються числа
а1= х2-х1 а2= у2-у1
y
Абсолютна величина
вектора а з координатами
(а1 ; а2 ) дорівнює
арифметичному
квадратному кореню із
суми квадратів його
координат.
В (х2;у2 )
A (х1;у1 )
x
11

12. Задача №1

ЗАДАЧА №1
Дано точки А(3;5) і В(-3;3). Знайдіть
координати вектора АВ.
ЗАДАЧА №2
Дано вектор а(3;4). Знайти
абсолютну величину вектора а.
12

13. Розв’язання №1

РОЗВ’ЯЗАННЯ №1
АВ(-3-3;3-5) =АВ(-6;-2).
Відповідь. АВ(-6;-2)
РОЗВ’ЯЗАННЯ №2
ІаІ =
=
=
Відповідь. ІаІ= 5.
13

14. Дії з векторами

ДІЇ З ВЕКТОРАМИ
Сумою векторів а і b з
координатами а1, а2 і
b1, b2 називається
вектор с з
координатами а1 + b1 ,
а2 + b2 , тобто
а(а1, а2 ) + b(b1, b2 ) =
= с(а1+ b1 ; а2 + b2 )
Закони додавання
а+0=а
а+b=b+а
а+(b+c)=(a+b)+c
b
а
с
c=a+b
14

15. Задача №3

ЗАДАЧА №3
Знайдіть координати вектора с, що є сумою
векторів а(4;8) і b(-4;5).
РОЗВ’ЯЗАННЯ
Нехай с(c1; с2 ).
c1 =а1+ b1 ; c1 = 4 – 4= 0;
С2 = а2 + b2 ; С2 = 8 + 5=13.
Отже с(0;13).
Відповідь. с(0;13)
15

16. Додавання векторів

ДОДАВАННЯ ВЕКТОРІВ
Правило
трикутника
Правило
паралелограма
В
А
В
С
•АВ+ВС=АС
А
С
D
•АВ+АD=АС
16

17. Віднімання векторів

ВІДНІМАННЯ ВЕКТОРІВ
Правило для
побудови
різниці двох
векторів
• Щоб побудувати вектор, який дорівнює
різниці векторів а і b, треба від однієї точки
відкласти вектори а і b, що дорівнюють їм.
Тоді вектор, початок якого збігається з
кінцем вектора b, а кінець – з кінцем
вектора а, буде різницею векторів а і b.
В
a
Побудова
А
a-b
b
С
АВ – АС = СВ
17

18. Задача №4 задача№5

ЗАДАЧА №4
Дано вектори а і b
(див.рис.). Побудувати
вектор: с = а + b.
ЗАДАЧА№5
Дано вектори а і b
(див.рис.). Побудувати
вектор: с = а - b.
b
а
b
а
18

19. Побудова №4 Побудова №5

ПОБУДОВА №4
b
ПОБУДОВА №5
a
a- b
b
а
b
19

20. Множення вектора на число.

МНОЖЕННЯ ВЕКТОРА НА ЧИСЛО.
Добутком вектора
(а1;а2) на число λ
називається вектор
(λа1; λа2), тобто
(а1;а2) λ=(λа1; λа2)
Закони множення
вектора на число
Для будь – якого
вектора а та чисел λ, μ
(λ + μ) а = λа + μа
Для будь – яких двох
векторів а і b та числа λ
λ (а + b ) = λ а +λb
20

21. Задача №6 задача №7

ЗАДАЧА №6
Дано вектори с (-3 ; 8 )
і b (4; 16). Обчислити
координати вектора
n = b + c.
ЗАДАЧА №7
Дано вектори d і b
( див. рис.). Побудувати
вектор m=2b.
b
d
21

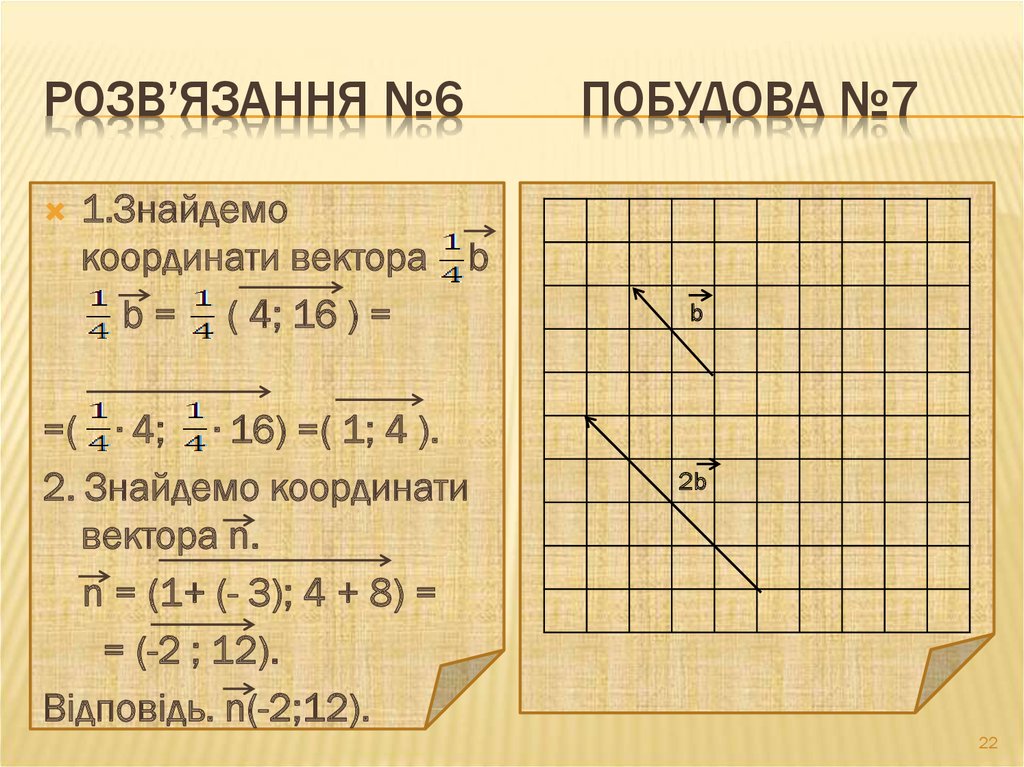
22. Розв’язання №6 побудова №7

РОЗВ’ЯЗАННЯ №6
1.Знайдемо
координати вектора
b = ( 4; 16 ) =
ПОБУДОВА №7
b
=( ∙ 4; ∙ 16) =( 1; 4 ).
2. Знайдемо координати
вектора n.
n = (1+ (- 3); 4 + 8) =
= (-2 ; 12).
Відповідь. n(-2;12).
b
2b
22

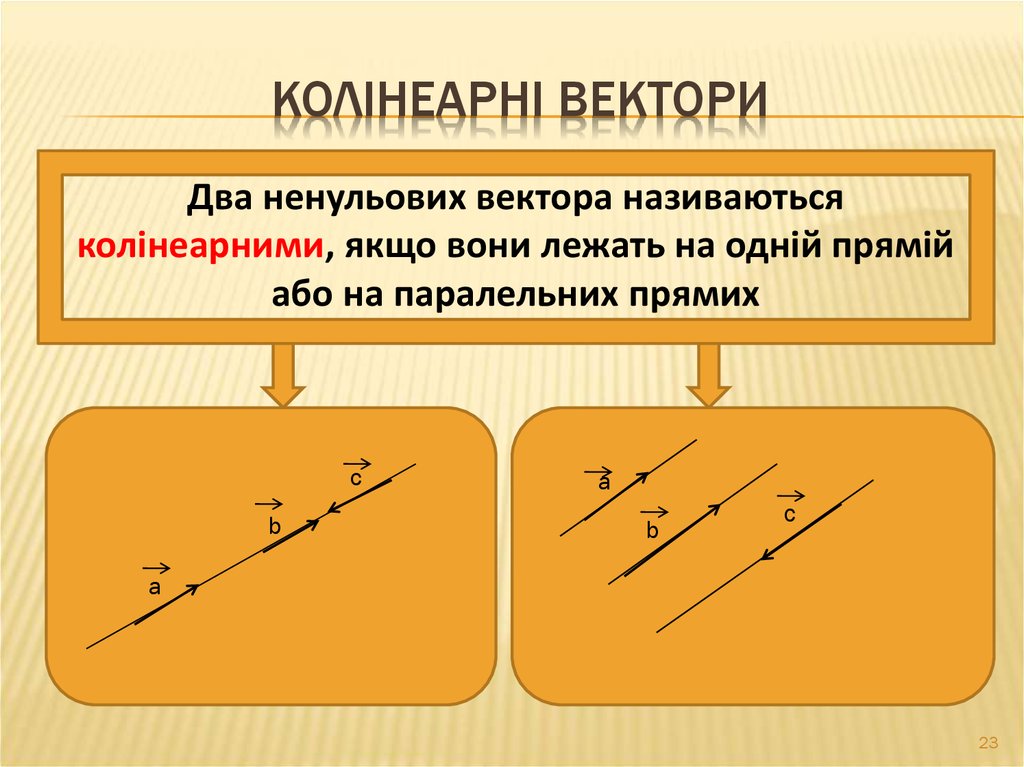
23. Колінеарні вектори

КОЛІНЕАРНІ ВЕКТОРИ
Два ненульових вектора називаються
колінеарними, якщо вони лежать на одній прямій
або на паралельних прямих
с
b
а
b
c
а
23

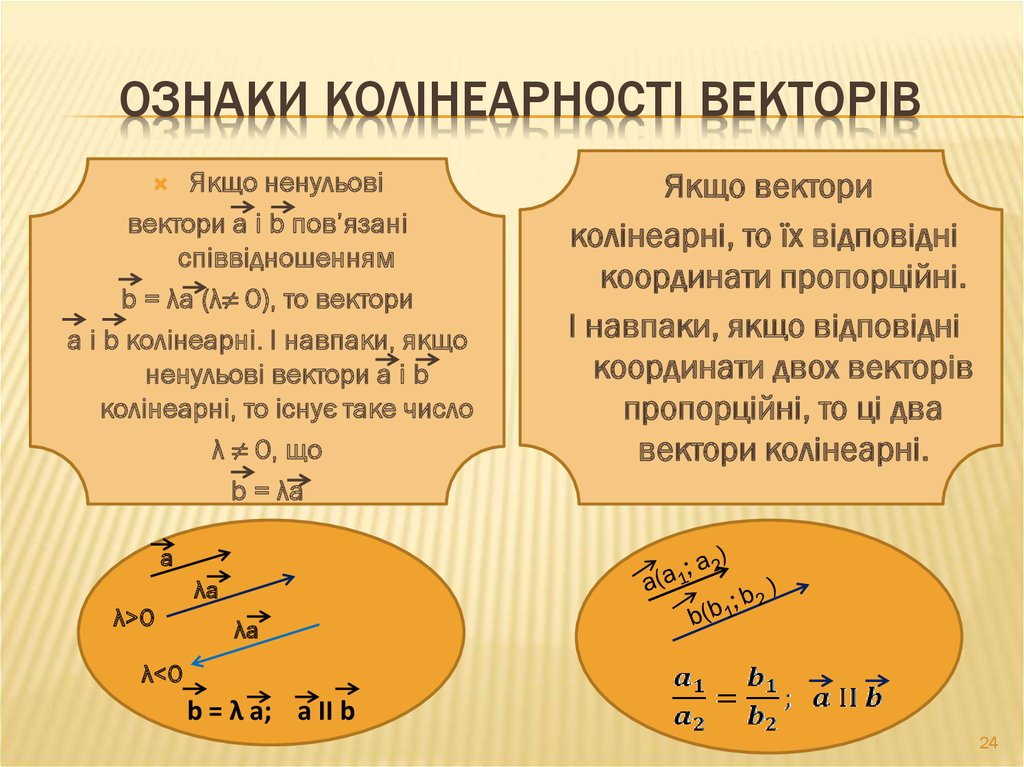
24. Ознаки колінеарності векторів

ОЗНАКИ КОЛІНЕАРНОСТІ ВЕКТОРІВ
Якщо ненульові
вектори а і b пов’язані
співвідношенням
b = λа (λ≠ 0), то вектори
а і b колінеарні. І навпаки, якщо
ненульові вектори а і b
колінеарні, то існує таке число
λ ≠ 0, що
b = λа
Якщо вектори
колінеарні, то їх відповідні
координати пропорційні.
І навпаки, якщо відповідні
координати двох векторів
пропорційні, то ці два
вектори колінеарні.
а
λ>0
λа
λа
λ<0
b = λ а; а II b
24

25. Задача № 8

ЗАДАЧА № 8
Дано
чотири точки А(3;0),
В(0;1), С(2;7) і D(5;6).
Доведіть, що вектори АВ і
СD колінеарні.
25

26. доведення

ДОВЕДЕННЯ
1.Знайдемо координати вектора АВ.
АВ (0-3;1-0) =АВ(-3; 1);
2.Знайдемо координати вектора СD.
СD (5 – 2;6 – 7) =СD(3;-1).
3. Якщо АВ ІІ СD і АВ(х1;х2 ), СD(у1;у2 ),
то
;
;
-1= -1,
було довести.
отже АВ ІІ СD, що й треба
26

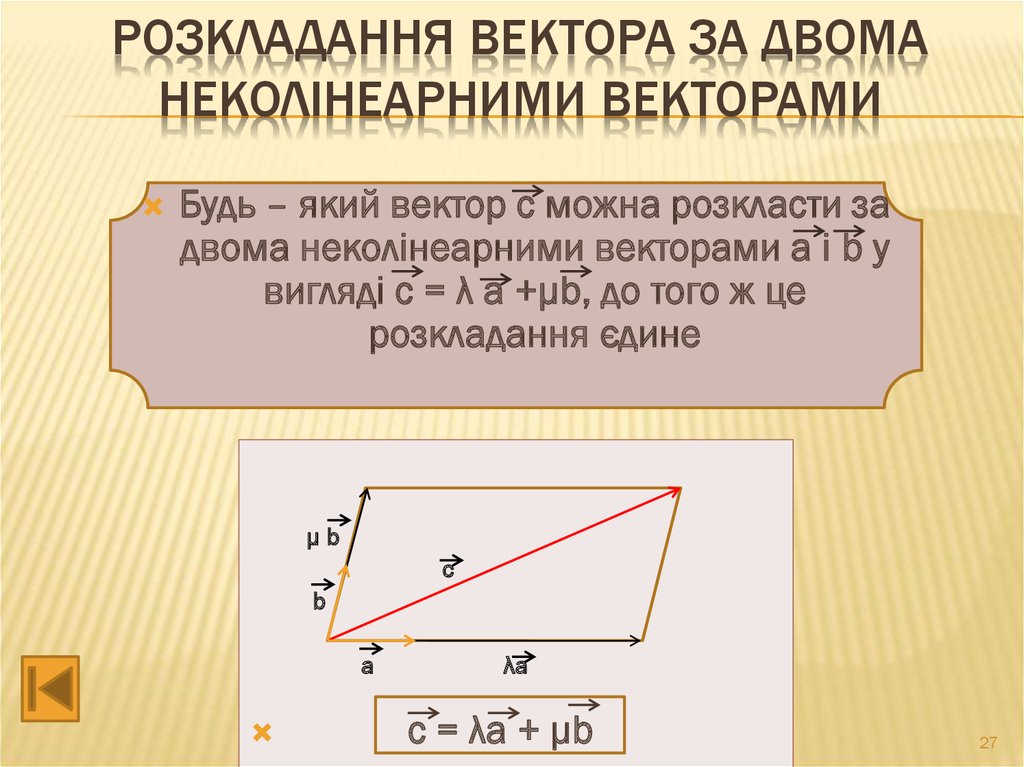
27. Розкладання вектора за двома неколінеарними векторами

РОЗКЛАДАННЯ ВЕКТОРА ЗА ДВОМА
НЕКОЛІНЕАРНИМИ ВЕКТОРАМИ
Будь – який вектор с можна розкласти за
двома неколінеарними векторами а і b у
вигляді с = λ а +μb, до того ж це
розкладання єдине
μb
с
b
а
λа
с = λа + μb
27

28. Скалярний добуток векторів

СКАЛЯРНИЙ ДОБУТОК ВЕКТОРІВ
Скалярним добутком векторів а(а1;а2) і b(b1;b2) називається
число а1b1+a2b2
а
β
b
Якщо а ∙ b = 0, то a b
28

29. Задача № 9 Задача № 10

ЗАДАЧА № 9
Знайти кут між
векторами а і b, якщо
І а І = 4√2, І b І = 3,
а ∙ b= 12.
ЗАДАЧА № 10
Довести, що вектори а і
с перпендикулярні,
якщо а(3;2), с(6;-9).
29

30. Розв’язання №9 Доведення №10

РОЗВ’ЯЗАННЯ №9
а ∙ b= І а І∙ І b І∙
;
;
=
β = 45˚
Відповідь : 45˚.
ДОВЕДЕННЯ №10
Якщо вектори
перпендикулярні, то їх
скалярний добуток
дорівнює нулю.
а ∙ с = 0,
а ∙ с = 3∙ 6 + 2 ∙ (-9)=
= 18 – 18 = 0,
тобто а с.
30