One-dimensional Photonic Crystals

1.

MIPT / PHYSTECH
One-dimensional
Photonic Crystals
Moscow Institute of Physics and Technology
Evgeny Ryabkov
06.12.2022

2.

Multilayer film
• ε(z) varies along the z axis only (one
dimension);
• Each layer is uniform and extends to infinity
along the x and y axes. The periodicity along
z extends to infinity;
• Bragg mirror for light within a frequency
within a specified range.
J. Joannopoulos, Photonic crystals:
molding the flow of light (Pinceton
Univ. Press,1995).
1

3.

Bloch’s theorem
• Bloch’s theorem: solutions to
the Schrödinger equation in a periodic
potential take the form of a plane
wave modulated by a periodic function:
• Stationary solution of the wave equation propagating in a periodic structure:
E(r, t) = U(r) exp[ikxx + ikyy + ikzz]exp[-iwt]
2

4.

Electromagnetic modes of a MF
• Infinite film consisting of 2
periodic layers with the
periodicity L = L1 + L2;
ε1, L1
ε2, L2
• Continuous symmetry along
the xy plane
• Discrete translational
symmetry in the z direction.
J. Joannopoulos, Photonic crystals: molding
the flow of light (Pinceton Univ. Press,1995).
3

5.

Electromagnetic modes of a MF
• The wave vector corresponding to xy plane can assume any value due to continuous
translational symmetry
• The wave vector kz can be restricted to a finite interval, the one-dimensional Brillouin
zone, due to discrete translational symmetry in the z direction;
• Kz = β for simplicity.
E(r, t) = U(r) exp[ikxx + ikyy]exp[iβt]
4

6.

Electromagnetic modes of a MF
• Solutions for (kx, ky) = 0;
• The solution in each film can be presented as a
pair of counter-propagating plane waves:
E(r) = ai εexp[ikiz] + biεexp[-ikiz]
Image courtesy of Denis G. Baranov
ε
where is a fixed polarization vector for on-axis propagation through the periodic
structure, and ai and bi are complex amplitudes of forward and backward propagating waves
5

7.

Transfer matrix method
fields in one film:
fields in 2 consecutive films:
Denis G. Baranov, Handbook on Theoretical Nanophotonics, in progress
6

8.

Transfer matrix method
The matrix describing propagation across films:
One can derive the interface transfer matrix
that relates the outgoing waves to the
incoming ones:
Denis G. Baranov, Handbook on Theoretical Nanophotonics, in progress
7

9.

Transfer matrix method
ri,j - complex Fresnel reflection coefficients
(for a particular polarization
state q = s; p) for incidence from medium i
onto medium j;
ti,j – complex transmission coefficients for
incidence from medium i into medium j.
Resolving the equation with respect to
an+1 and bn+1 one can get:
Denis G. Baranov, Handbook on Theoretical Nanophotonics, in progress
8

10.

Transfer matrix method
The resulting transfer-matrix of the system:
The reflection and transmission
coefficients of the entire system:
Denis G. Baranov, Handbook on Theoretical Nanophotonics, in progress
9

11.

Electromagnetic modes of a MF
The relationship for the given unit cell takes the form:
- In the case of two altering films
The Bloch’s phase factor must be equal to the eigenvalue of the composite transfer matrix of the unit cell
10

12.

Electromagnetic modes of a MF
The characteristic equation for determining the extended
modes of 1D photonic crystals
The general solution of this characteristic
equation can be written as
Extended modes are not localized in any part of the system and propagate freely without attenuation
11

13.

Electromagnetic modes of a MF
Photonic band gaps – regions with no allowed
modes in the crystal (the wave vector is
imaginary).
The right hand-plot shows that the gap widens
considerably as the dielectric constant is increased.
J. Joannopoulos, Photonic crystals: molding
the flow of light (Pinceton Univ. Press,1995).
12

14.

Band gaps
The physical mechanism behind the emergence of
bandgaps is the total reflection of the Bloch wave by
each unit cell, which makes propagation in the periodic
structure impossible.
Band gaps in terms of reflectance
Courtesy of Denis G. Baranov
13

15.

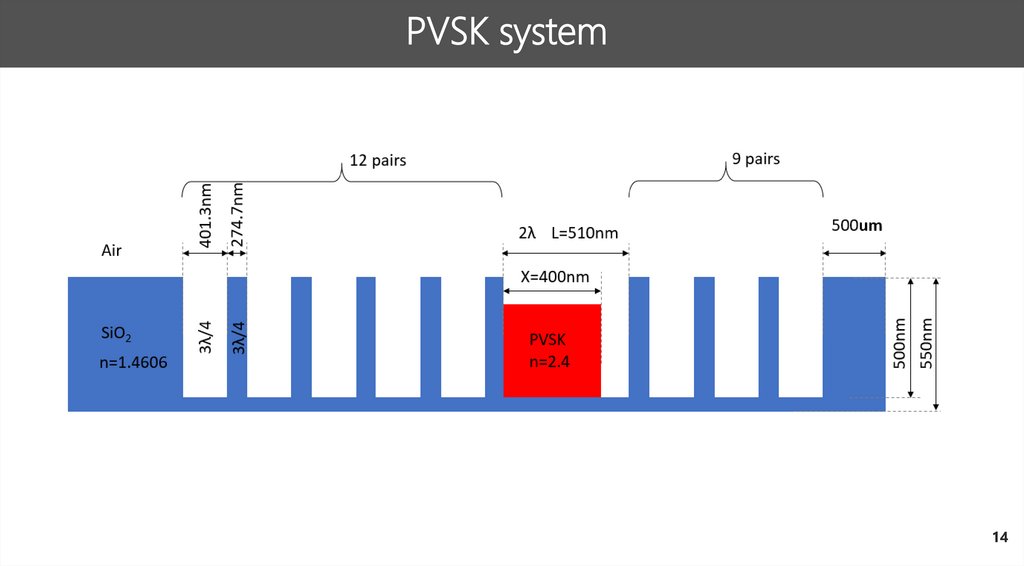
PVSK system
14

16.

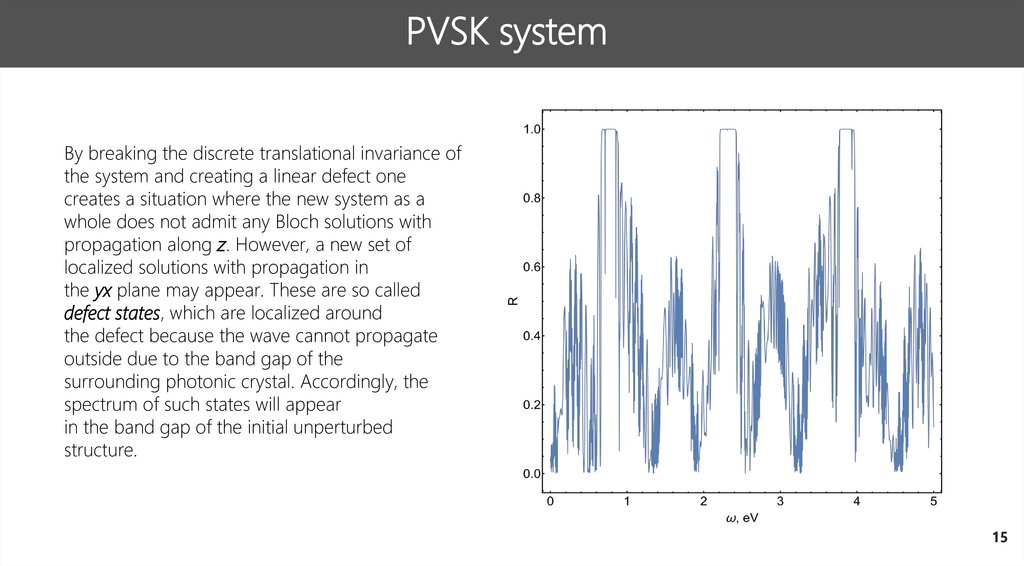
PVSK system
By breaking the discrete translational invariance of
the system and creating a linear defect one
creates a situation where the new system as a
whole does not admit any Bloch solutions with
propagation along z. However, a new set of
localized solutions with propagation in
the yx plane may appear. These are so called
defect states, which are localized around
the defect because the wave cannot propagate
outside due to the band gap of the
surrounding photonic crystal. Accordingly, the
spectrum of such states will appear
in the band gap of the initial unperturbed
structure.
15

17.

17