Similar presentations:
Алгебра и начала анализа. Радианная мера углов
1. Алгебра и начала анализа
Радианная мерауглов
Воробьев Леонид Альбертович, г.Минск
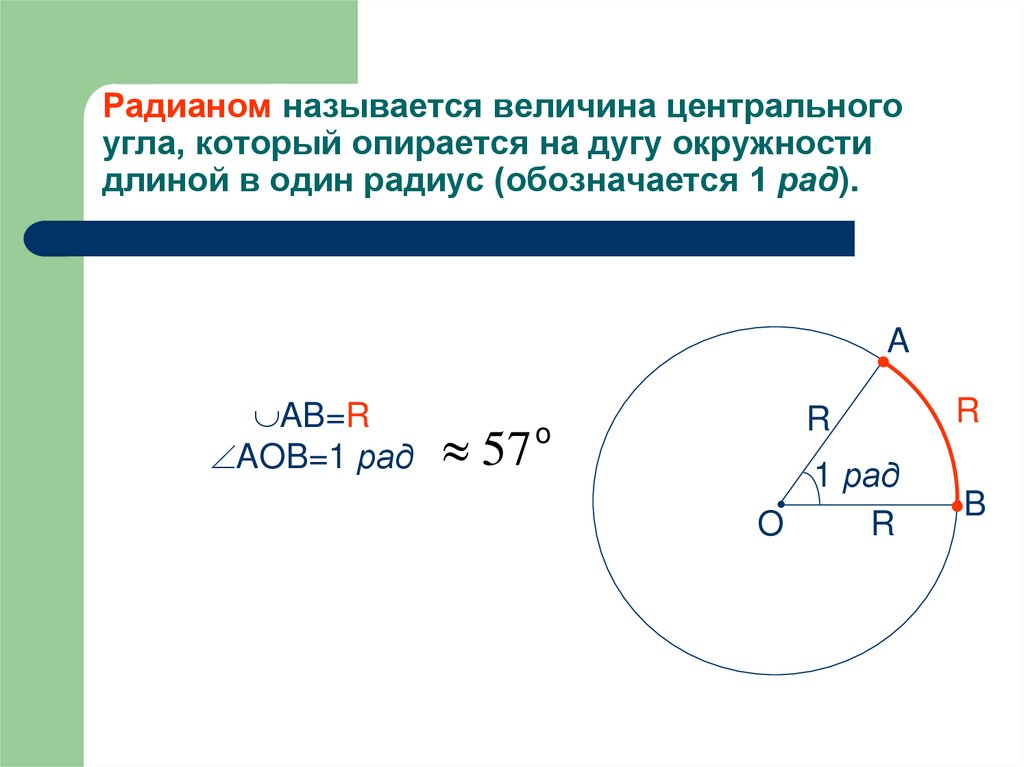
2. Радианом называется величина центрального угла, который опирается на дугу окружности длиной в один радиус (обозначается 1 рад).
AAB=R
AOB=1 рад
57
o
R
R
1 рад
O
R
B
3.
Перевод из градусной меры в радианную инаоборот
α0= α0·
Пример:
0
180
правило перевода из
градусной меры в радианную;
рад
20 20
20
180 9
180
α рад= α· 180
Пример:
0
правило перевода из
радианной меры в градусную.
180 180
36
5 5
5
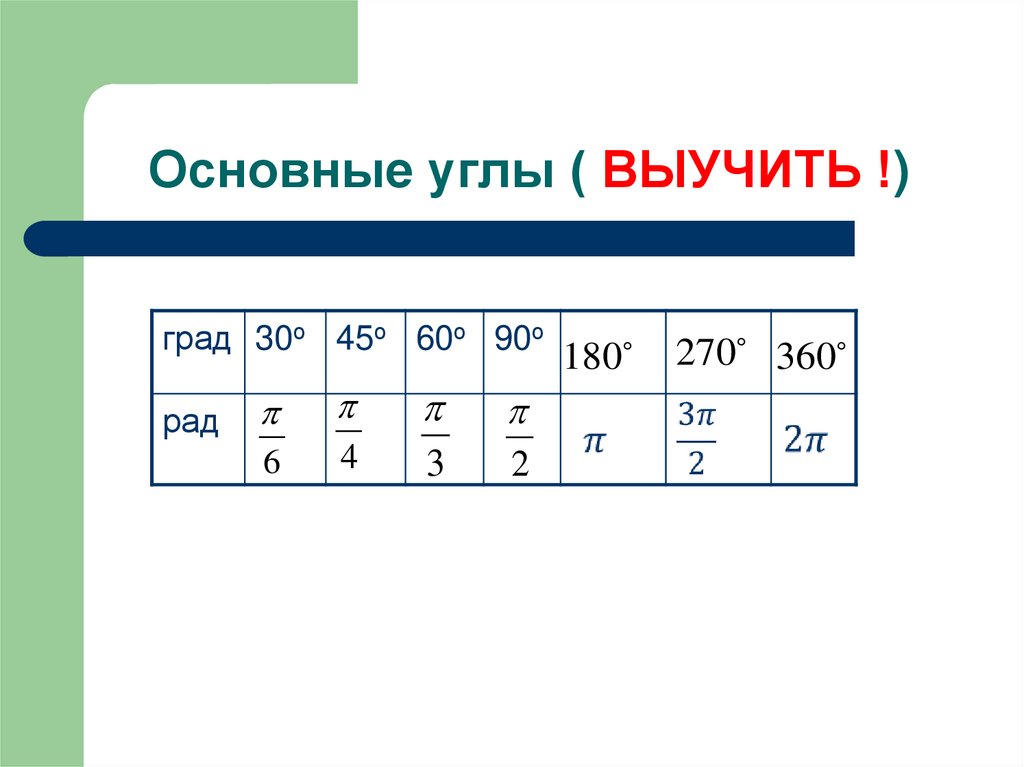
4. Основные углы ( ВЫУЧИТЬ !)
град 30о 45о 60о 90орад
6
4
3
2
180
270 360
5.
Найти градусную меру угла,выраженного в радианах:
1.
150о
2.
135о
3.
120о
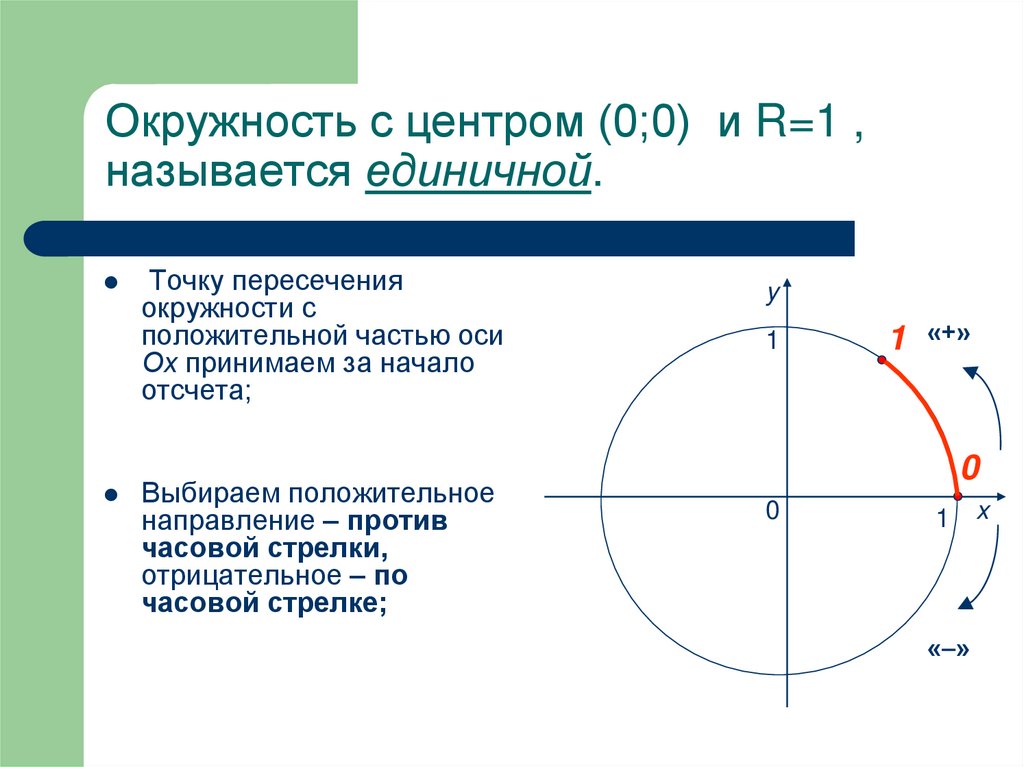
6. Окружность с центром (0;0) и R=1 , называется единичной.
Точку пересеченияокружности с
положительной частью оси
Ох принимаем за начало
отсчета;
Выбираем положительное
направление – против
часовой стрелки,
отрицательное – по
часовой стрелке;
y
1
1 «+»
0
0
1
« »
x
7. Напомним, что декартова система разбивается координатными осями на четыре координатные четверти – I, II, III и IV.
Задание 2. Определитеграницы координатных
четвертей через углы
поворота в градусной мере,
взятых в положительном
направлении.
Задание 3. Выполните
предыдущее задание, при
условии, что выбирается
отрицательное
направление углов
поворота.
y
1
II
1
I
0
0
III
1
IV
x
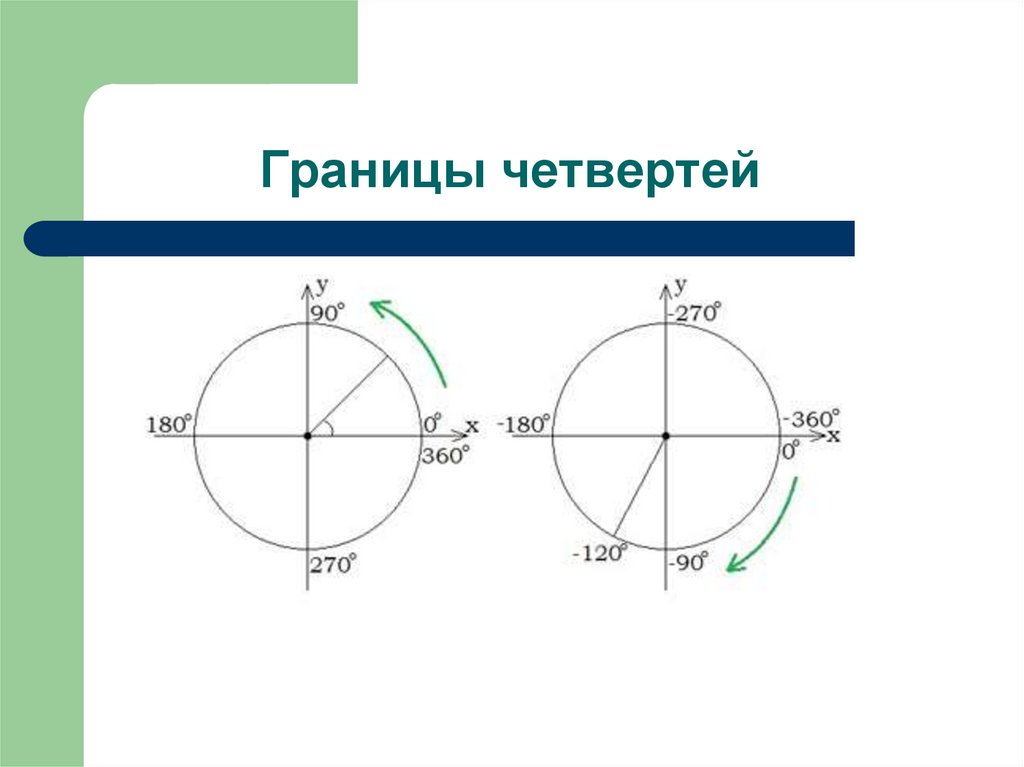
8. Границы четвертей
9.
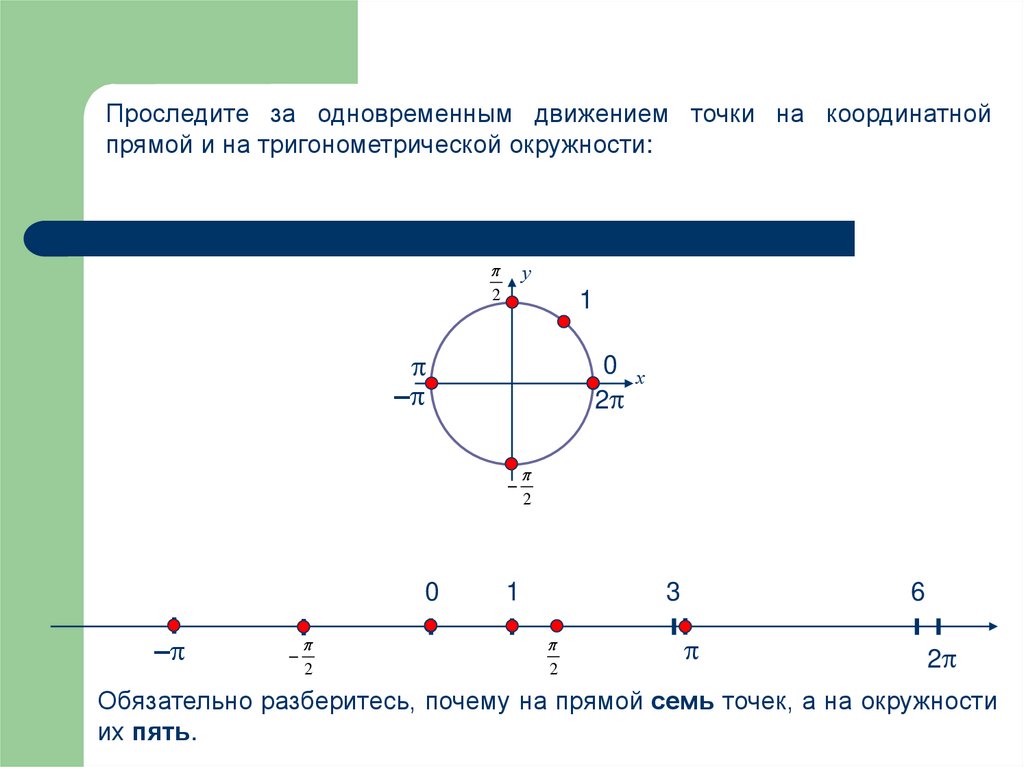
Проследите за одновременным движением точки на координатнойпрямой и на тригонометрической окружности:
2
у
1
–
0 х
2
0
–
2
2
1
3
2
6
2
Обязательно разберитесь, почему на прямой семь точек, а на окружности
их пять.
10. В какой четверти находится угол:
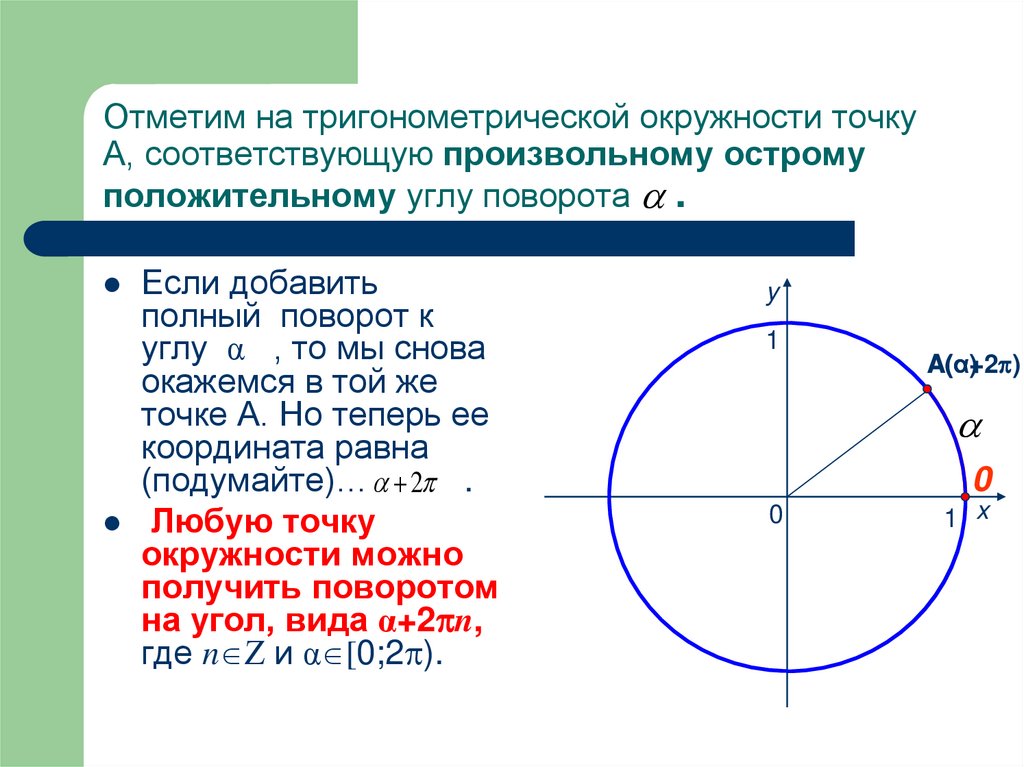
Отметим на тригонометрической окружности точкуА, соответствующую произвольному острому
положительному углу поворота .
Если добавить
полный поворот к
углу α , то мы снова
окажемся в той же
точке А. Но теперь ее
координата равна
(подумайте)… 2 .
Любую точку
окружности можно
получить поворотом
на угол, вида α+2 n,
где n и α [0;2 ).
y
1
A(α)
A(α+2 )
0
0
1 x
11. Отметим на тригонометрической окружности точку А, соответствующую произвольному острому положительному углу поворота .
В какой четверти углы:790 0 = 360 . 2 + 70
= 700 - Iч
-9100 = - ( 360 . 2 + 190) = - 1900 – II ч
12000 = 360 . 3 + 120 = 1200 - IIч






 mathematics
mathematics