Similar presentations:
Радианная мера угла
1.
9 класс2.
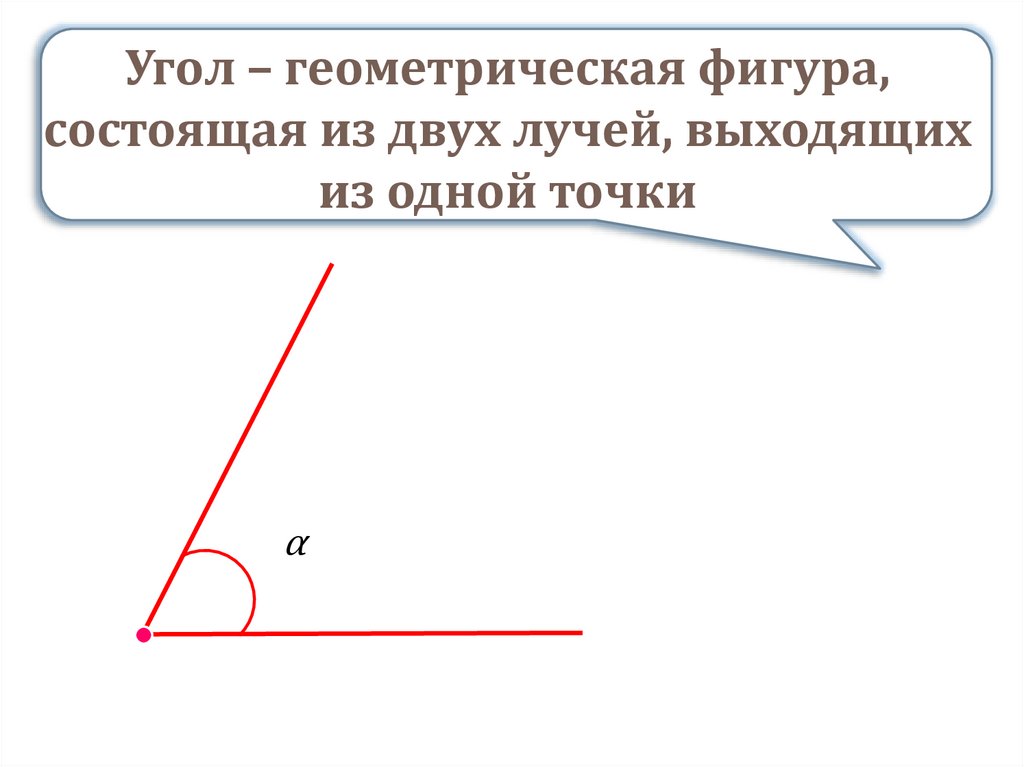
Угол – геометрическая фигура,состоящая из двух лучей, выходящих
из одной точки
α
3.
Измерение углов60
0
4.
Развитие тригонометриивызвало необходимость в 19
веке введения новой меры
измерения угловрадианной.
Число Пи – математическая
константа, которая выражает
отношение длины окружности к
её диаметру
5.
6.
7.
о8.
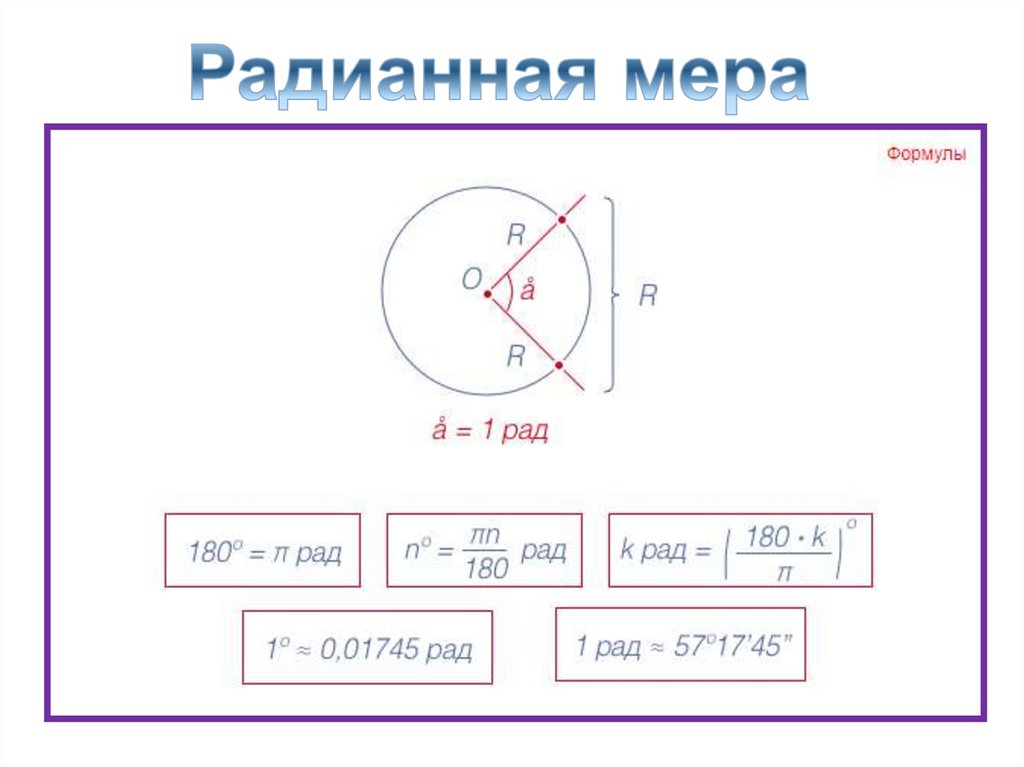
Радиан (от латинского radius - спица колеса)9.
10.
11.
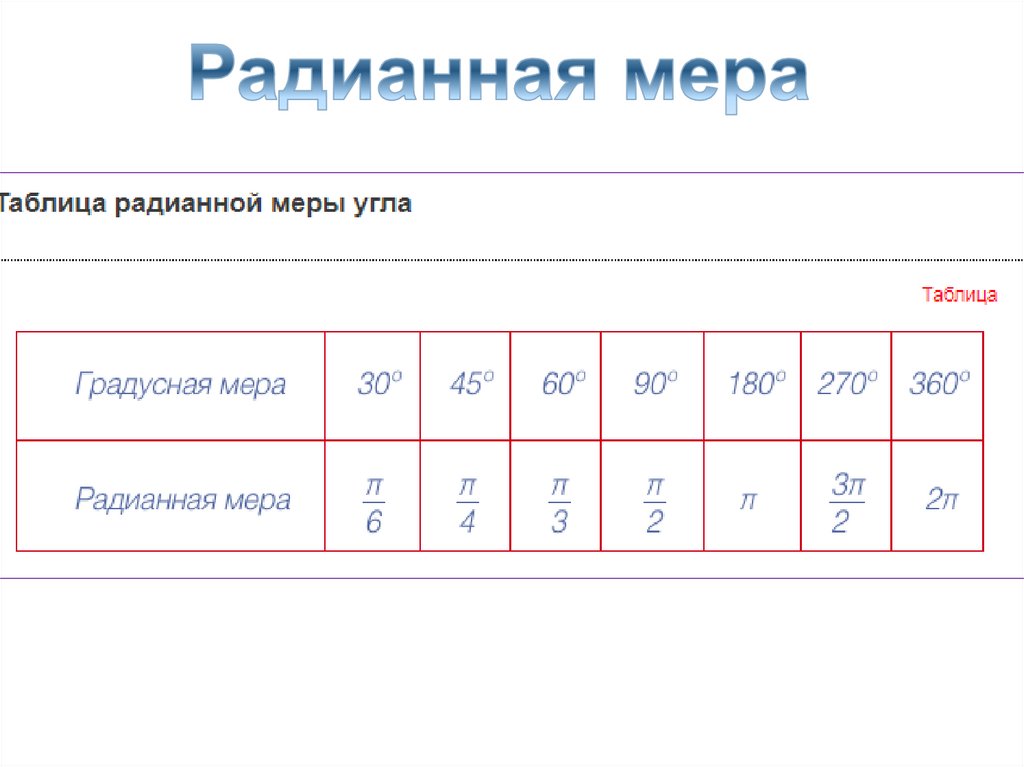
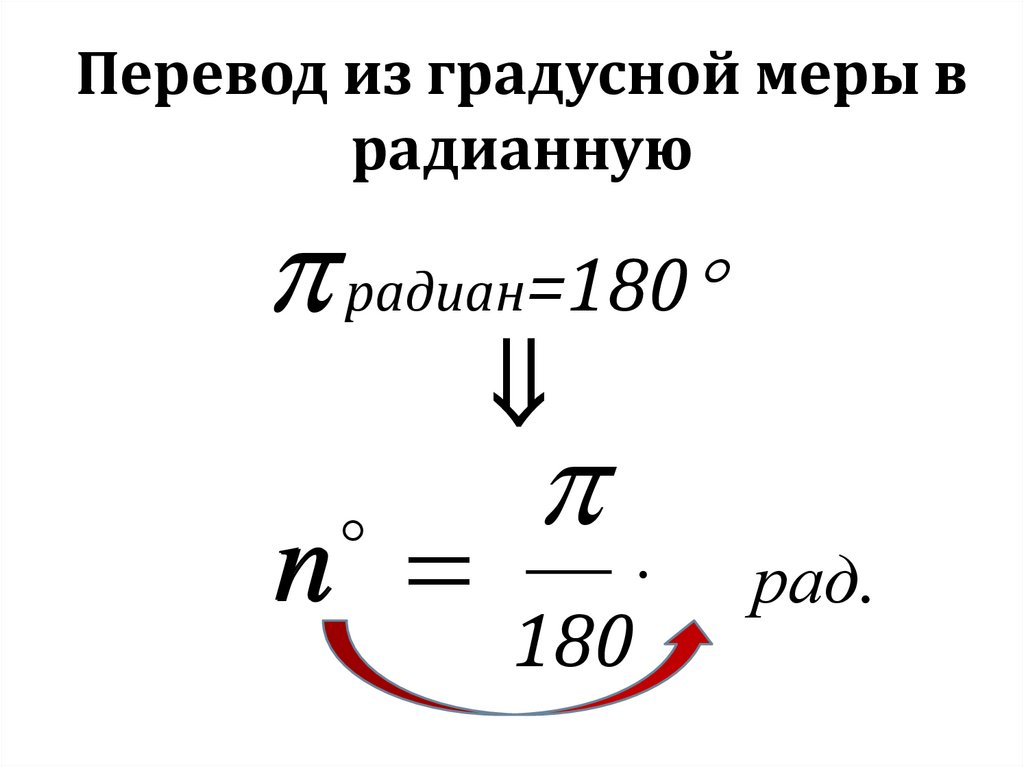
Перевод из градусной меры врадианную
радиан=180
рад.
1
180
12.
Перевод из градусной меры врадианную
радиан=180
n
180
рад.
13.
Примеры:1. 60
60
рад.
рад.
3
180
90
рад
.
рад
.
2. 90
180
2
3
135
рад
.
3. 135
рад
.
4
180
14.
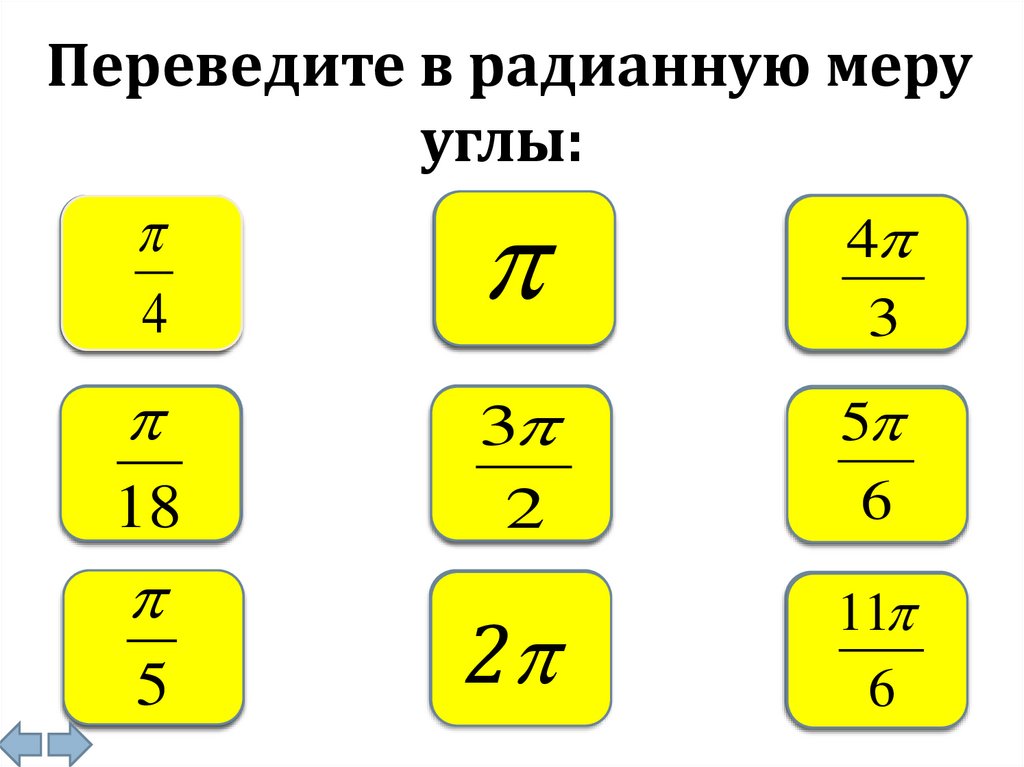
Переведите в радианную мерууглы:
4
45
180
240
10
3
270
2
5
150
6
360
2
11
330
6
4
18
36
5
3
15.
Перевод из радианной меры вградусную
радиан=180
a m
180
16.
Примеры:180
1.
рад.
18
10
10
180
2.
рад.
20
9
9
4 180
4
240
3.
рад.
3
3
17.
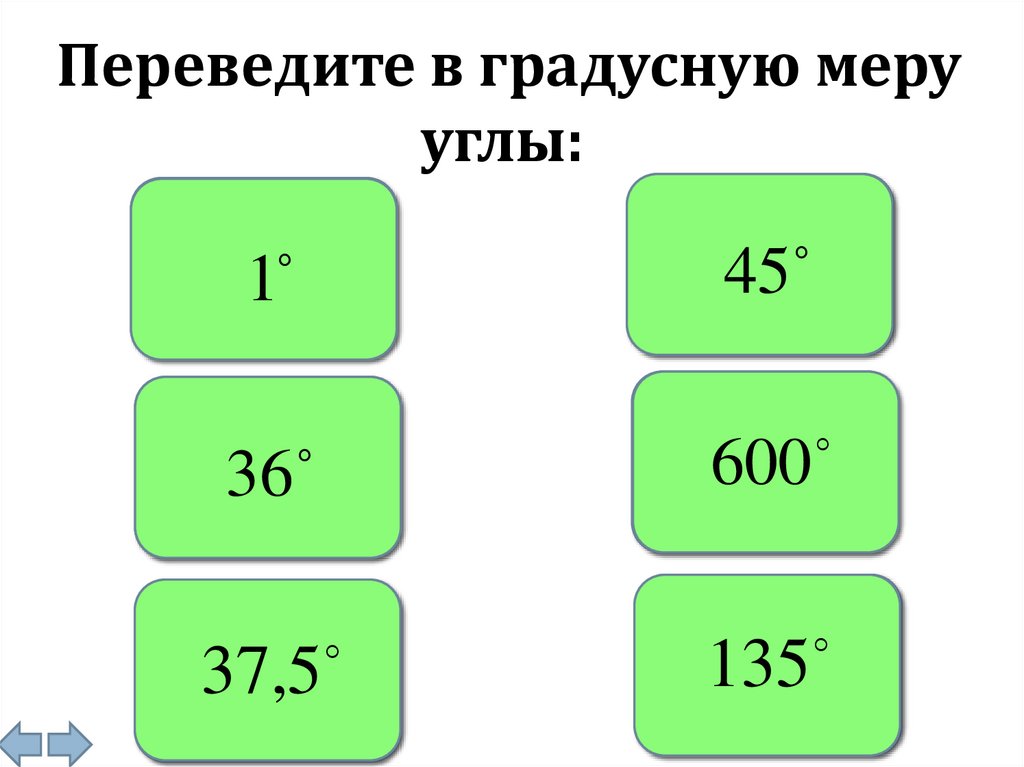
Переведите в градусную мерууглы:
рад
.
1
180
.
рад
36
5
5
37,рад
5 .
24
4
.
рад
45
10
600
рад.
3
3
рад.
135
4
18.
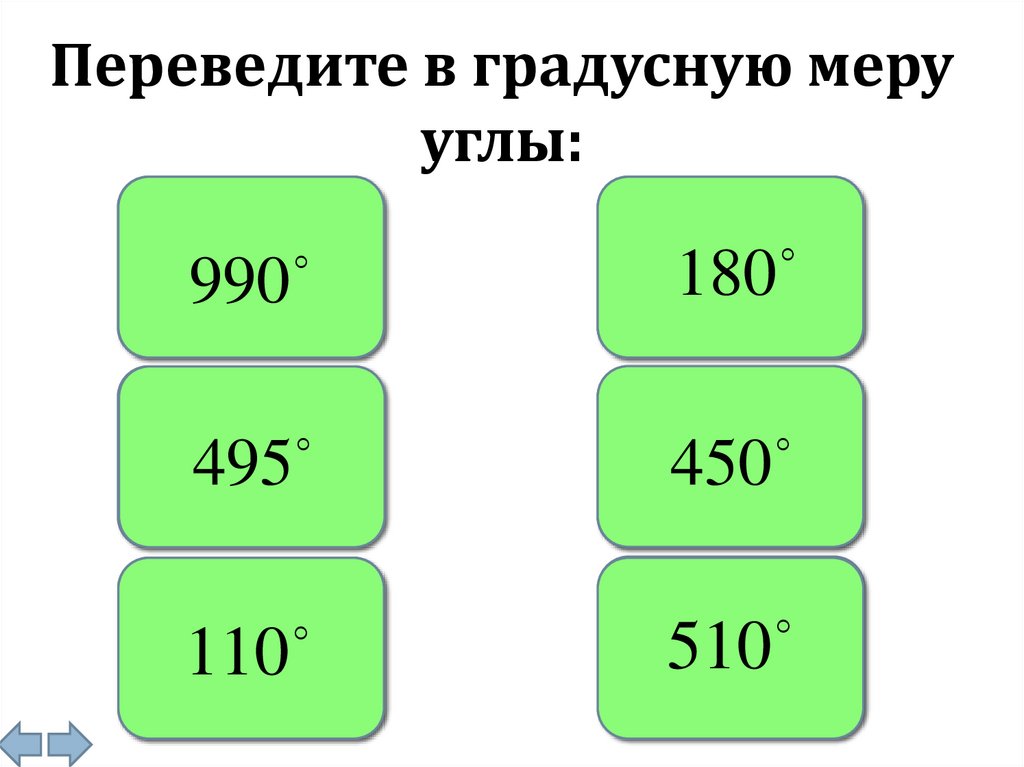
Переведите в градусную мерууглы:
11
рад.
990
2
11
рад.
495
4
11
110рад.
18
180
рад.
5
рад.
450
2
17
510рад.
6
19.
Перевод из градусной меры врадианную:
n
n
180
рад
.
Перевод из радианной меры в
градусную:
m рад. m 180
20.
21.
Единичная окружностьОкружность с центром в начале системы координат Oxy и
Положительное
Отрицательное
Точку
пересечения
радиусом,
равным
единице, называется единичной, а
направление поворота:
направление
поворота:
окружности
с – тригонометрическим.
ограниченный
ей круг
против часовой стрелки.
по
часовой стрелке.
y частью оси
положительной
Ох 0принимают за начало
3200
497
отсчета
540
O
+
x
–
22.
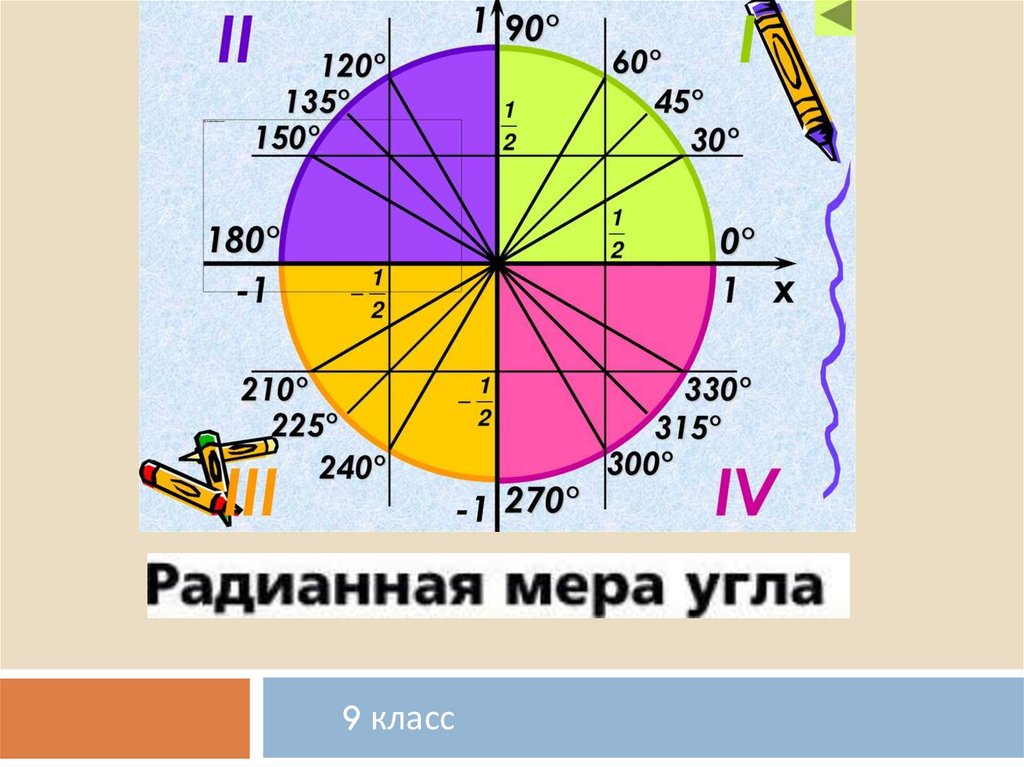
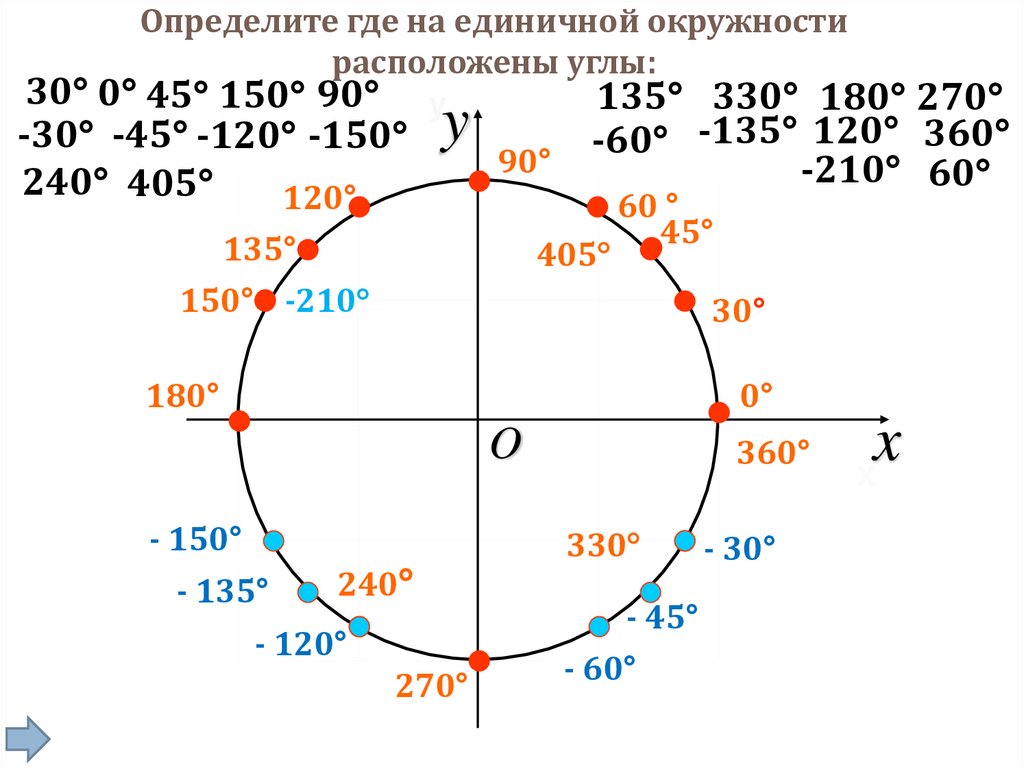
Определите где на единичной окружностирасположены углы:
30 0 45 150 90 у
135 330 180 270
-30 -45 -120 -150
240 405
120°
y
90°
135°
150° -210
-60 -135 120 360
-210 60
405
60 °
45°
30°
180°
0°
O
- 150°
- 135°
240
- 120°
270°
360°
330
- 45°
- 60°
- 30°
x
Х
23.
Расположите на единичной окружности углы:3
4
2
17
3
4
19
6
3
4
11
4
6
2
2
3
5
6
у
2
5
6
3
3
4
17
4
x
19
6
3
4
2
3
2
11
6
4
24.
Единичная окружностьII четверть
y
90 ° < < 180 °
2
O
I четверть
0° < < 90°
0
2
180° < < 270°
270° < < 360°
3
2
3
2
2
III четверть
IVчетверть
x
25.
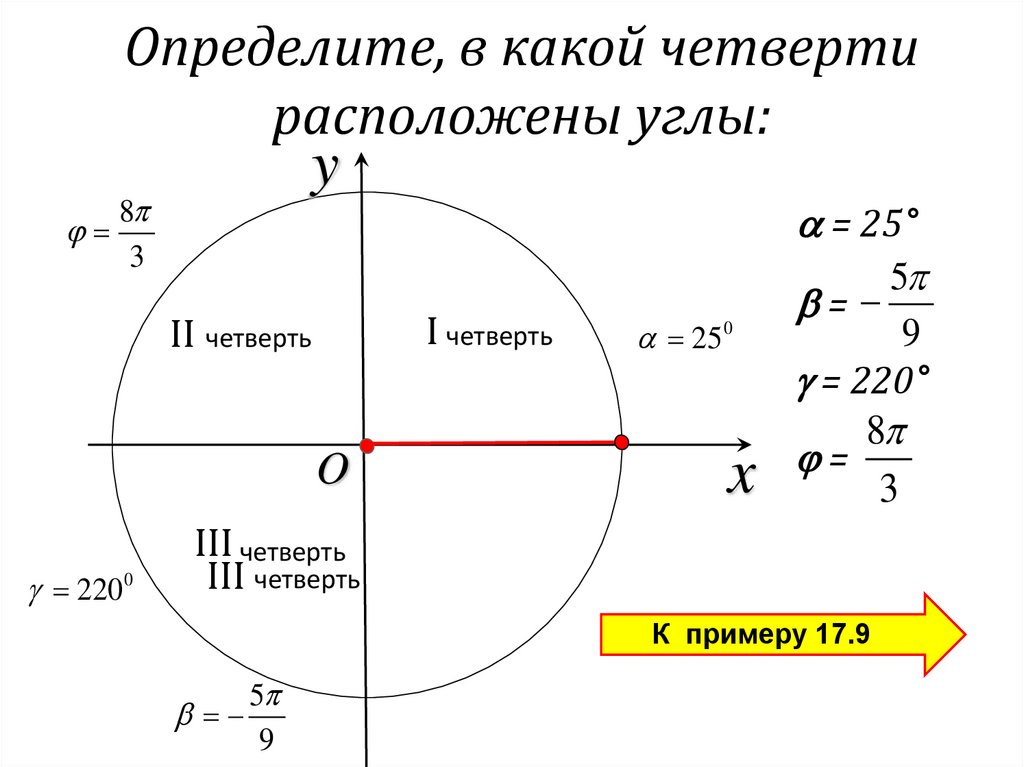
Определите, в какой четвертирасположены углы:
y
8
3
I четверть
II четверть
O
220 0
25 0
x
= 25°
5
=
9
= 220°
8
=
3
III четверть
III четверть
К примеру 17.9
5
9
26.
РЕШЕНИЕ1) IV; 2) IV; 3) III; 4) IV; 5) I; 6) II
РЕШЕНИЕ
1) 0,-1; 2) -1,0; 3) 0,1; 4) 0,1; 5) 0,1; 6) 1,0
27.
РЕШЕНИЕ1) 0,-1; 2) -1,0; 3) 0,-1; 4) -1,0; 5) -1,0
28.
РЕШЕНИЕ1)
3
;
;
2
2
2)
; ;
29.
К каждому из 3х углов , показанных на рис.17.8, необходимо множествозначений, связанных с множеством соответствующих единичных
окружностей ,например, для
30.
К каждому из 3х углов , показанных на рис.17.9, необходимо добавитьмножество значений, связанных с множеством соответствующих
единичных окружностей ,например, для
31.
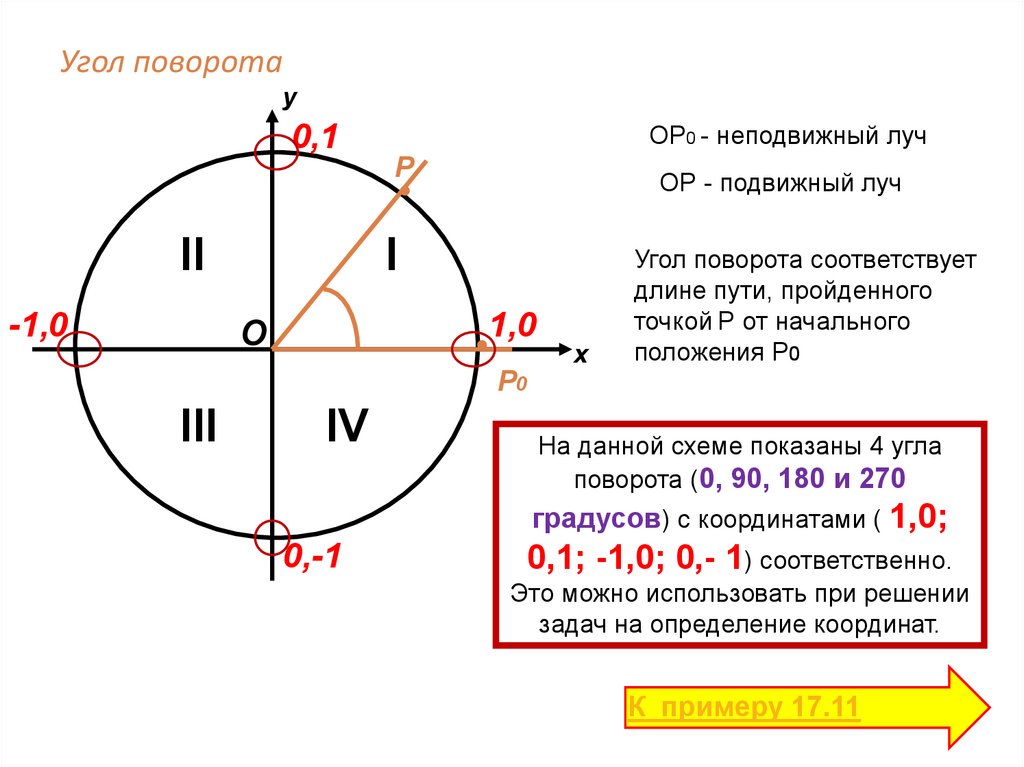
Угол поворотау
0,1
II
-1,0
ОР0 - неподвижный луч
Р
ОР - подвижный луч
I
1,0
О
Р0
III
IV
х
Угол поворота соответствует
длине пути, пройденного
точкой Р от начального
положения Р0
На данной схеме показаны 4 угла
поворота (0, 90, 180 и 270
градусов) с координатами ( 1,0;
0,-1
0,1; -1,0; 0,- 1) соответственно.
Это можно использовать при решении
задач на определение координат.
К примеру 17.11
32.
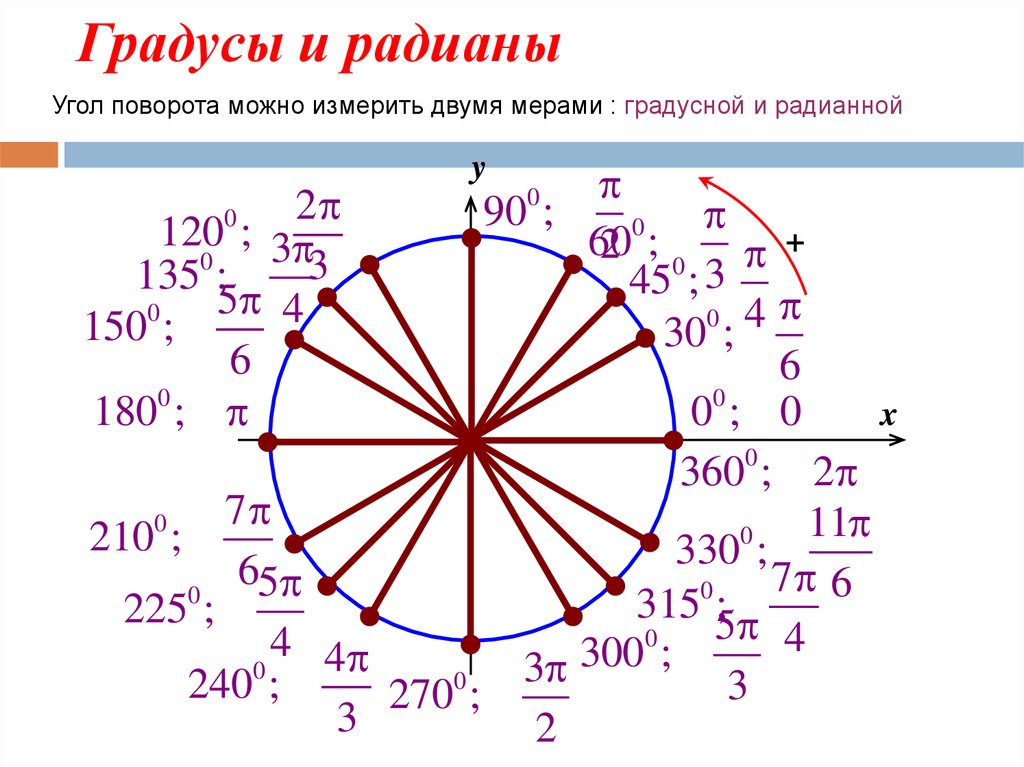
Градусы и радианыУгол поворота можно измерить двумя мерами : градусной и радианной
2
90
;
0
0
120 ; 3
60
;0 +
2
0
3
3
135 ;
45
;
5 4
0
0 4
150 ;
30 ;
6
6
x
00 ; 0
1800 ;
0
0
360 ; 2
7
0
11
0
210 ;
330
;
65
7 6
0
0
315 5;
225 ;
0
4
4 4
300
;
3
0
2400 ;
3
270 ;
3
2
y
0
33.
Градусы и радианыy
3
270 ;
2
0
1800 ;
00 ; 0
x
0
30 ;
6
0
45 ;
0
4
60
;
0
3
90 ;
2
0
-
34.
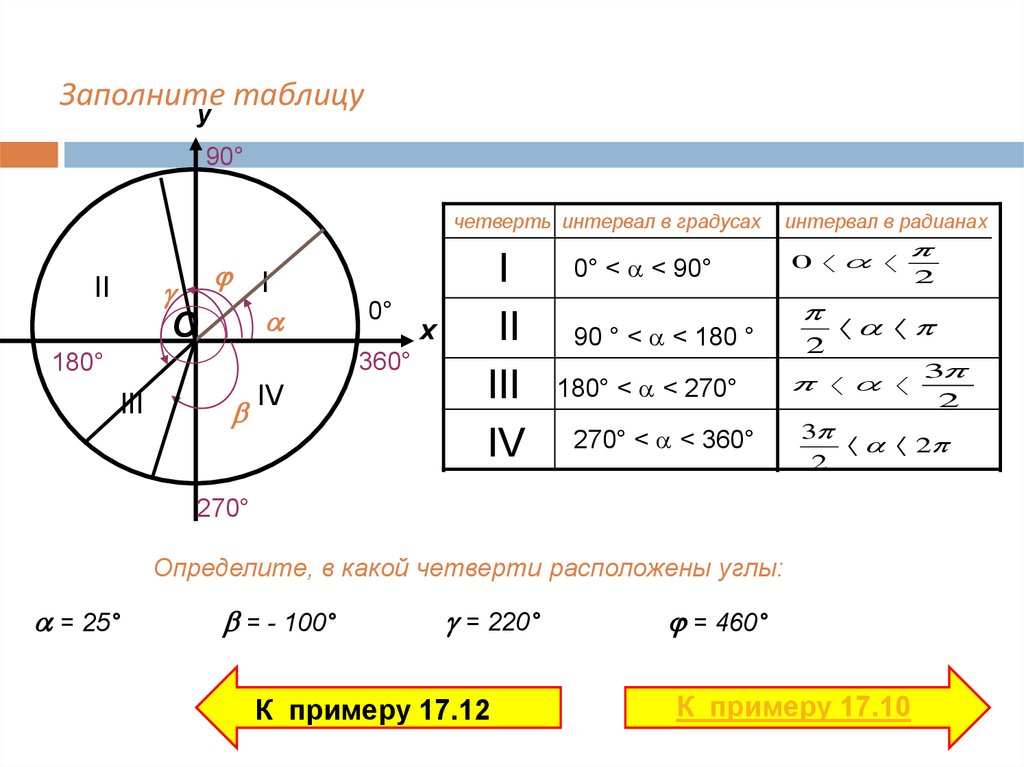
Заполните таблицуу
90°
четверть интервал в градусах
I
25
О
II
0°
360°
180°
III
IV
х
I
II
III
IV
0° < < 90°
90 ° < < 180 °
180° < < 270°
270° < < 360°
интервал в радианах
0
2
Определите, в какой четверти расположены углы:
= - 100°
= 220°
К примеру 17.12
3
2
3
2
2
270°
= 25°
2
= 460°
К примеру 17.10







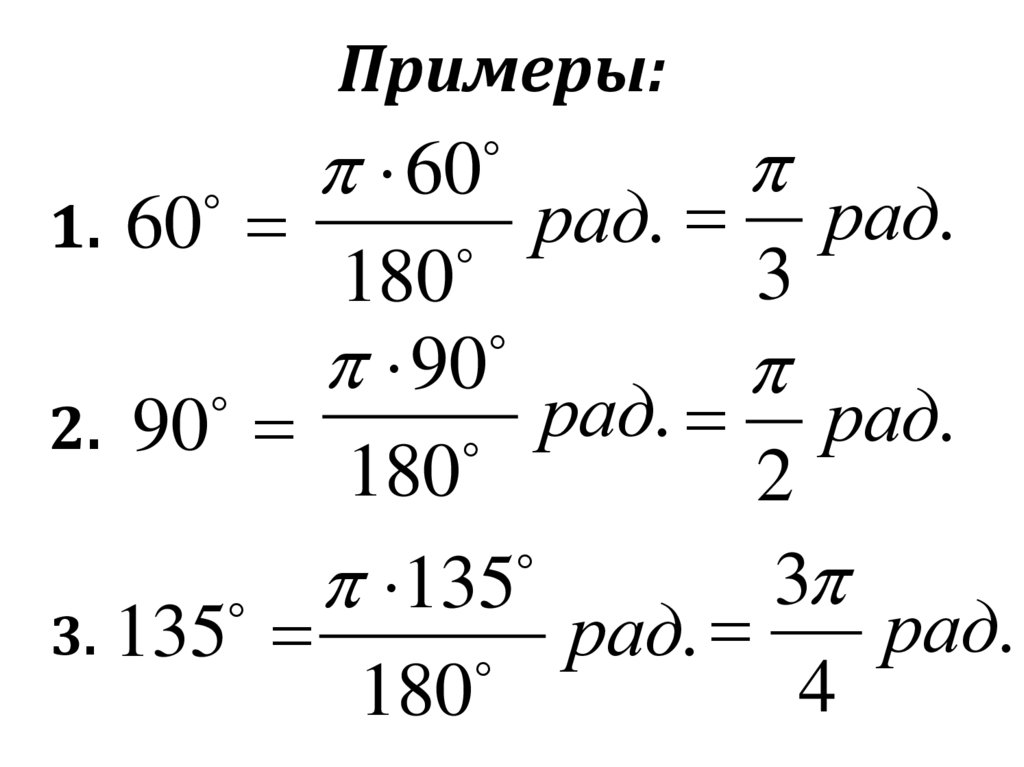

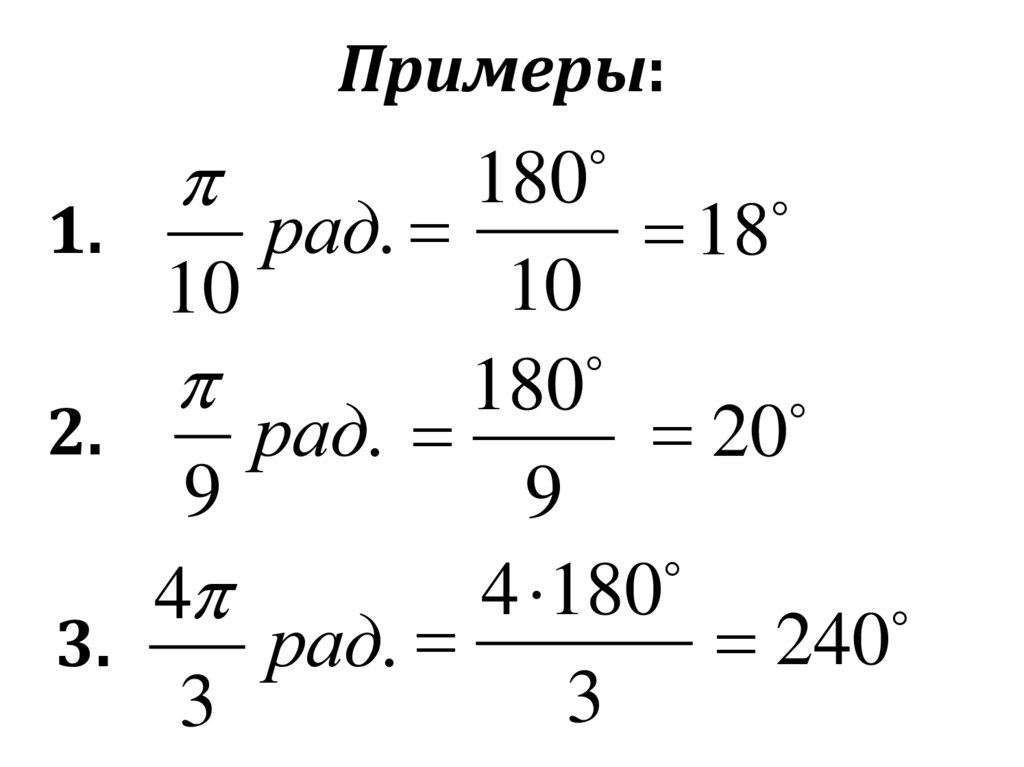
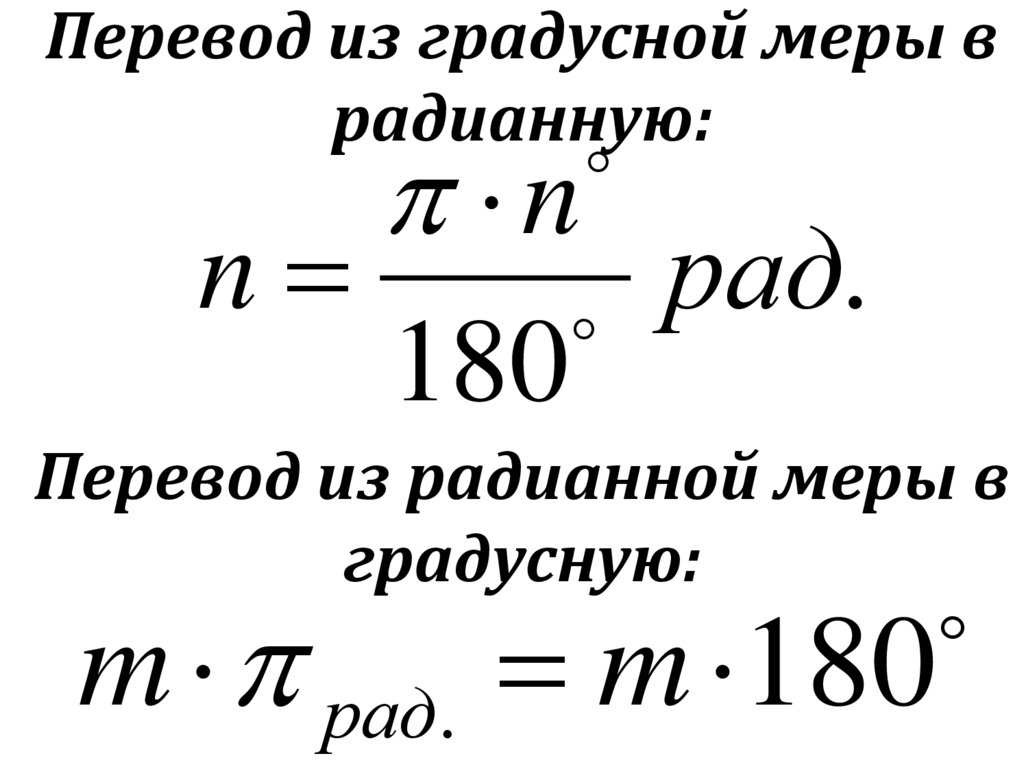










 mathematics
mathematics