Similar presentations:
Радианная мера угла
1. Тема 2: Радианная мера угла.
2.
В тетради построй единичную окружность через точку Ау
-270° 90°
-180°
А360°
х
0°-360°
О
180°
-90°
270°
3. Задание 1:(выполнить в тетради)
• На единичной окружностиизобразить угол поворота, равный
150°, -45°, -135°.
Задание 2:(перечертить в тетрадь
содержание следующего слайда)
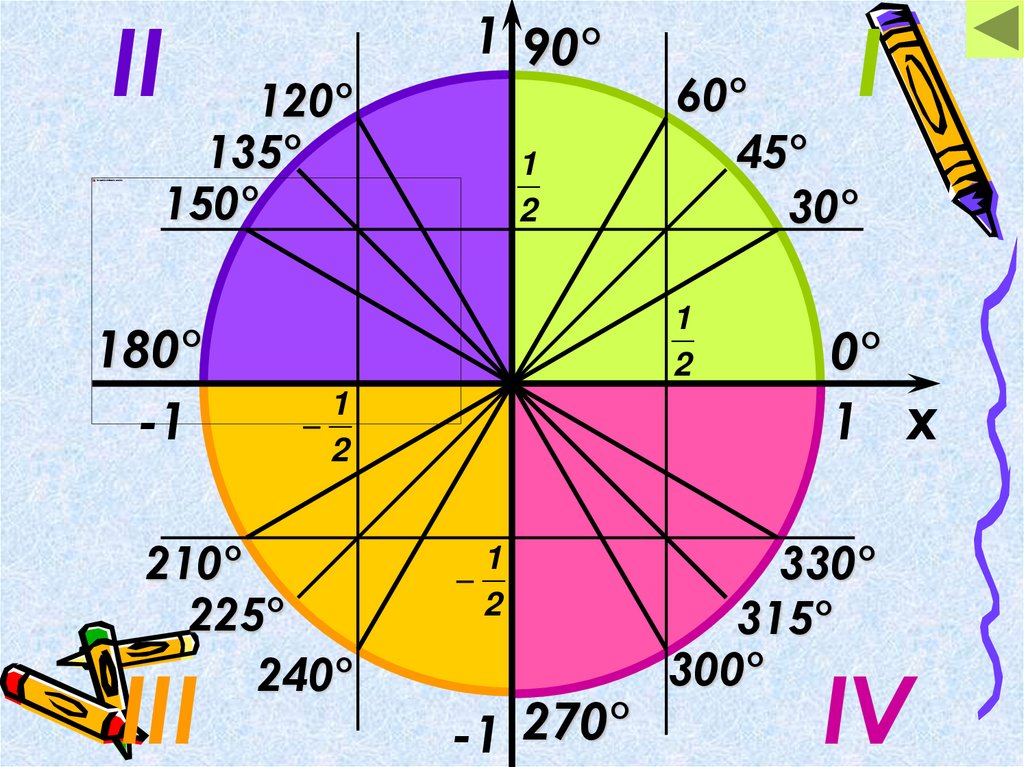
4.
II120°
135°
150°
180°
-1
1
2
I
60°
45°
30°
1
2
1
2
210°
225°
240°
III
1 90°
1
2
-1 270°
0°
1 x
330°
315°
300°
IV
5.
II четверть180°
О
у
90°
I четверть
В
α
Так, если 0° ‹ α ‹ 90°, то α-угол I четверти
если 90° ‹ α ‹ 180°, то α-угол II четверти;
А
если 180° ‹ α ‹ 270°, то α-угол III четверти;
0° х
если 270° ‹ α ‹ 360°, то α-угол IV четверти.
270°
III четверть
IV четверть
Углы 0°, ±90°, ±180°, ±270°, ±360° не относятся
ни к какой четверти.
Подумай: Угол в 430° является углом какой четверти ?
т.к. 430°= 360°+70° и 0 °‹ 70°‹ 90°, то этот угол лежит в I
четверти.
Так, например, угол в 920° является углом III четверти, т.к.
920 °=360°▪ 2+200 °
6. Задание 3:(запиши)
• Углом какой четверти являетсяугол α, если:
α=283°, 190°, -20°, -110°, 550 °, -730°.
7.
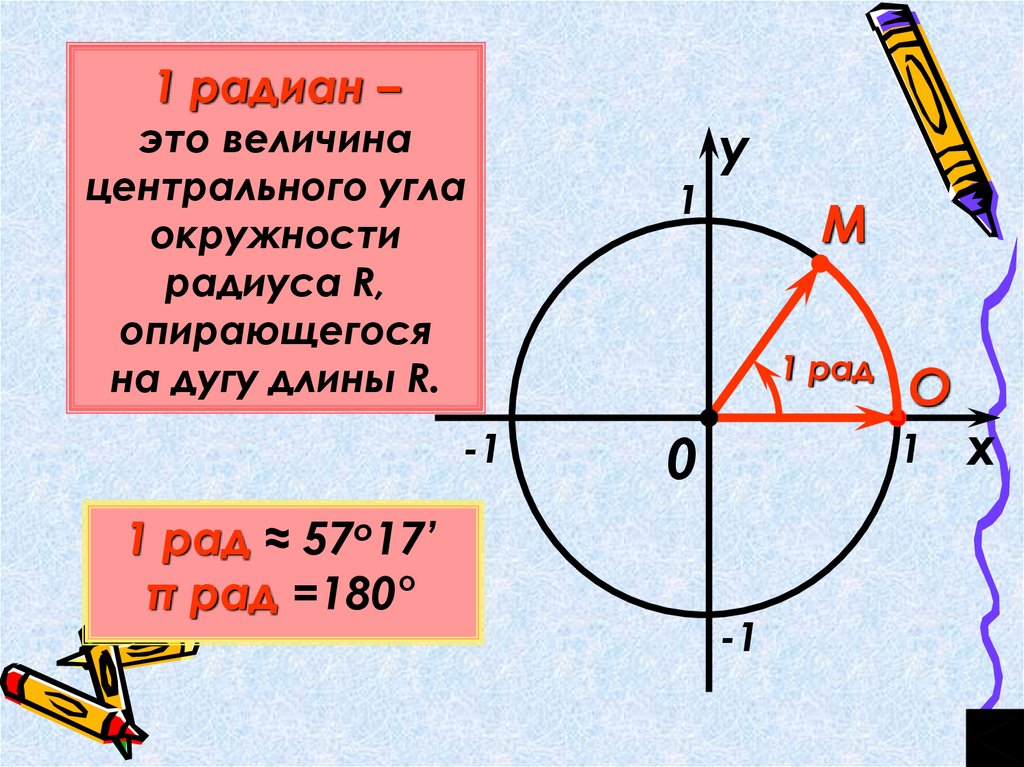
1 радиан –это величина
центрального угла
окружности
радиуса R,
опирающегося
на дугу длины R.
-1
1 рад ≈ 57о17’
π рад =180°
1
y
M
1 рад
0
О
1
-1
x
8. Перевод градусной меры в радианную
πα = α
180o
30°=?
90°=?
60°=?
9. Перевод радианной меры в градусную
π4
o
180
α рад = α
π
3π
2
π
6
10.
11.
Дадим определение синуса, косинуса, тангенса икотангенса произвольного угла α.
Пусть при повороте около точки О на угол α
начальный радиус АО переходит в радиус ОВ.
у
В(х; у)
R
О
α
А
Синусом угла α называется отношение
ординаты точки В к длине радиуса.
х
х
Sin α= у
R
у
В(х; у)
Косинусом угла α называется отношение
абсциссы точки В к длине радиуса.
x
Cos α= R
О
RR
α
А
х
12.
Тангенсом угла α называетсяотношение ординаты точки В к ее
абсциссе.
у
В(х; у)
О
α
А
tg α= y
x
х
у
Котангенсом угла α называется отношение
абсциссы точки В к ее ординате.
ctg α=
x
y
В(х; у)
О
α
А
х
13.
№0 Мизинец№1 Безымянный
№2 Средний
№3 Указательный
№4 Большой
00
300
450 sin
600
900
α
=
n
2
14.
Значение синуса№ пальца
Угол α
Расчет по формуле
0
0
1
30
sin 30 0
2
45
sin 450
3
60
4
90
0
0
2
sin 0 0
1
1
2
2
2
2
sin 60 0
sin 90 0
3
2
4
1
2
15.
Значение косинуса№ пальца Угол α
4
0
3
30
2
45
1
60
0
90
Расчет по формуле
cos 0 0
4
1
2
cos 30 0
cos 450
3
2
2
2
cos 60 0
1
1
2
2
cos 90 0
0
0
2
16.
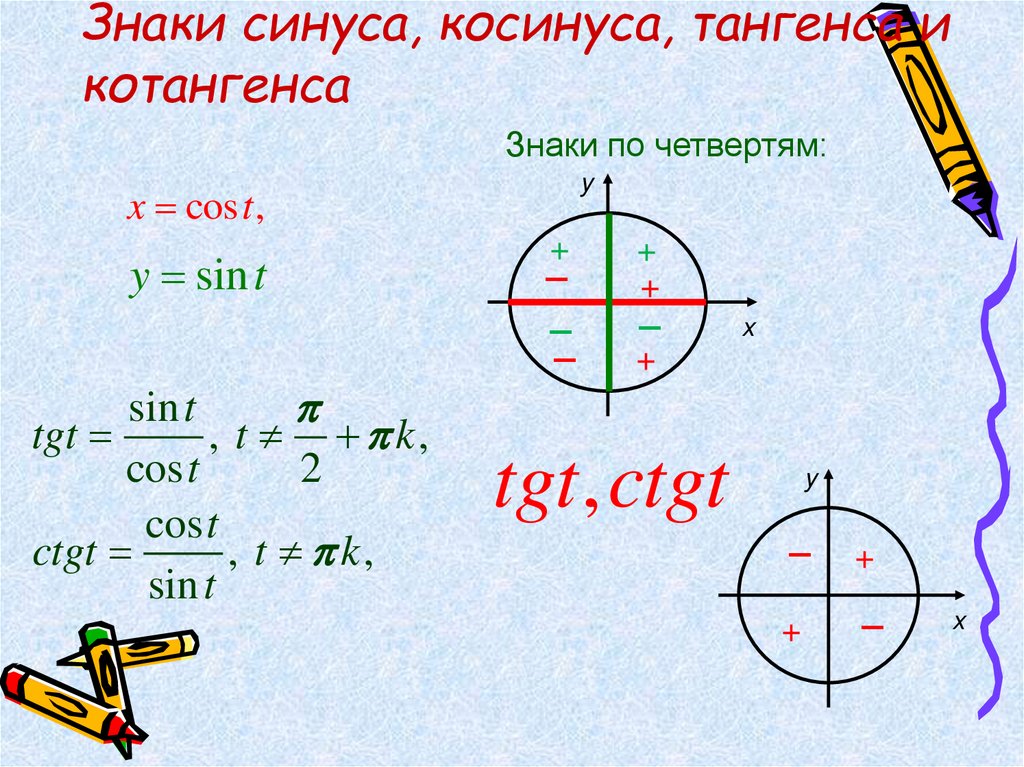
Знаки синуса, косинуса, тангенса икотангенса
Знаки по четвертям:
y
x cos t ,
y sin t
sin t
tgt
, t k,
cos t
2
cos t
ctgt
, t k,
sin t
+
–
–
–
+
+
–
x
+
tgt , ctgt
y
–
+
+
–
x













 mathematics
mathematics








