Радианный метод измерения углов вращения и связь с градусной мерой

1. Радианный метод измерения углов вращения и связь с градусной мерой

2. Контрольные вопросы

1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
Что такое тригонометрия?
Что называют единичной окружностью?(сделайте чертеж и запишите
порядок квадрантов)
Какие углы называют углами вращения?(продемонстрируйте на чертеже
положительные и отрицательные углы)
Опишите и продемонстрируйте на чертеже как отметить на единичной
окружности угол 225 0
Опишите и продемонстрируйте на чертеже как отметить на единичной
окружности угол 120 0
Какой угол равен 1 радиан?(продемонстрируйте на чертеже)
Запишите формулы перевода из градусной меры в радианную и
наоборот
Составьте таблицу наиболее часто встречающихся углов в градусах и
радианах
Разберите и запишите решение примера 1.
Разберите и запишите решение примера 2.

3. ТРИГОНОМЕТРИЯ

(от др.-греч. τρίγωνον «треугольник»
и μετρέω «измеряю», то
есть измерение треугольников) —
раздел математики, в котором
изучаются тригонометрические
функции и их использование
в геометрии

4. Единичная окружность

Единичная окружность — окружность, центр которой расположен в
начале координат и радиус которой равен 1.
Единичную окружность с установленным соответствием между
действительными числами и точками окружности называют числовой
окружностью.
Запомните порядок расположения
координатных четвертей (квадрантов)!

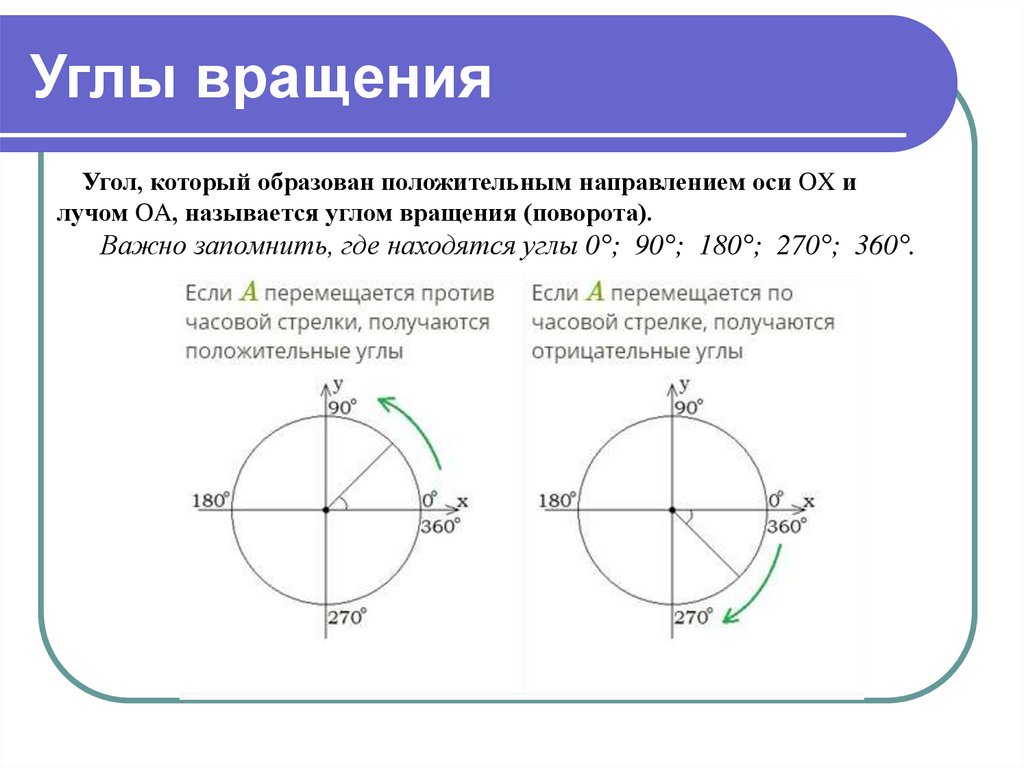
5. Углы вращения

Угол, который образован положительным направлением оси OX и
лучом OA, называется углом вращения (поворота).
Важно запомнить, где находятся углы 0°; 90°; 180°; 270°; 360°.

6. Углы вращения

7. Углы вращения

8. Радианная мера угла

Понятие угла и его градусного измерения известно из курса
планиметрии .
Вместе с тем, в математике наравне с градусной мерой угла
используется радианная.
Возьмем на координатной плоскости окружность с центром в
точке О и радиусом R. Отметим на ней дугу РМ, длина которой
равна R и угол РОМ.
Центральный угол, опирающийся на дугу,
длина которой равна радиусу окружности,
называется углом в 1 радиан.

9. Радианная мера угла

Так как дуга длиной πR (полуокружность), стягивает
центральный угол в 180°, то дуга длиной R, стягивает угол
в π раз меньший, т.е.
И наоборот
Так как π = 3,14, то 1 рад = 57,3°

10. Формулы перевода из градусной меры в радианную и наоборот

Если угол содержит a радиан, то его градусная мера равна
И наоборот
Обычно при обозначении меры угла в радианах наименование
«рад» опускают.
Например, 360° = 2π рад, пишут 360° = 2π

11. Радианная мера угла

Полезно помнить следующую сравнительную таблицу
значений наиболее часто встречающихся углов в
градусах и радианах:

12. Пример 1.

Найти радианную меру угла равного
а) 40° , б)120° , в)105°
Решение
а) 40° = 40·π / 180 = 2π/9
б) 120° = 120·π/180 = 2π/3
в) 105° = 105·π/180 = 7π/12

13. Пример 2.

Найти градусную меру угла, выраженного в радианах
а) π/6 , б) π/9, в) 2·π/3
Решение
а) π/6 = 180°/6 = 30°
б) π/9 = 180°/9 = 20°
в) 2π/3 = 2·180°/6 = 120°