Similar presentations:
Слайд-лекции по дисциплине «Высшая математика»
1.
Инновационный Евразийский университетКафедра «Математика»
Слайд-лекции по дисциплине
«Высшая математика»
Для студентов 2 курса ТГТ группы ПРПИ-19 и ТОРА -19
2020-2021 уч. г.
2. Линейная алгебра
Система двух линейных уравнений с двумя неизвестными и понятиеопределителя 2-го порядка.
Определители 3-го порядка, вычисление и свойства.
Система двух линейных уравнений с тремя неизвестными.
Правило Крамера.
Система
трех однородных
линейных уравнений с тремя
неизвестными.
Понятие определителя n-го порядка.
Обобщение формулы Крамера на случай системы n - линейных уравнений.
Понятие матрицы. Линейные операции над матрицами.
Обратная матрица.
Решение системы линейных уравнений матричным способом.
Ранг матрицы.
Теорема Кронеккера-Капелли.
Решение систем линейных уравнений методом Гаусса
3. Понятие определителя 2-го порядка
Определитель второго порядка, соответствующий таблицеэлементов
a1
a2
b1
, определяется равенством
b2
D det
a1
b1
a2
b2
a1b2 a2b1
где a1 и b2 – элементы главной диагонали,
a2 и b1 – элементы побочной диагонали
Пример
4. Системы 2-х линейных уравнений с 2-мя неизвестными
a1x b1 y c1a2x b2 y c 2
x
b1
b2
y
a1
a2
5. Варианты решений
Δ≠0– система имеет единственное решениех
х
,
у
у
- формулы Крамера
Δ=0, Δx≠0, Δу ≠0, Δz ≠0- система не имеет решения
Δ=0, Δx=0, Δу =0, Δz =0-система имеет бесконечное
множество решений
6. Определители 3-го порядка, вычисление и свойства
Определитель третьего порядка, соответствующий таблицеэлементов
a1
a2
a
3
b2
a1
b1
c1
a2
b2
c2 a1 b2 c3+ a2 b3 c1+ a3 b1 c2- a3 b2 c1- a1 b3 c2- a2 b1 c3
a3
b3
c3
b1
b3
c1
c 2 , определяется равенством
c 2
где a1 ,b2 и c3 – элементы главной диагонали,
a3 ,,b2 и c1 – элементы побочной диагонали
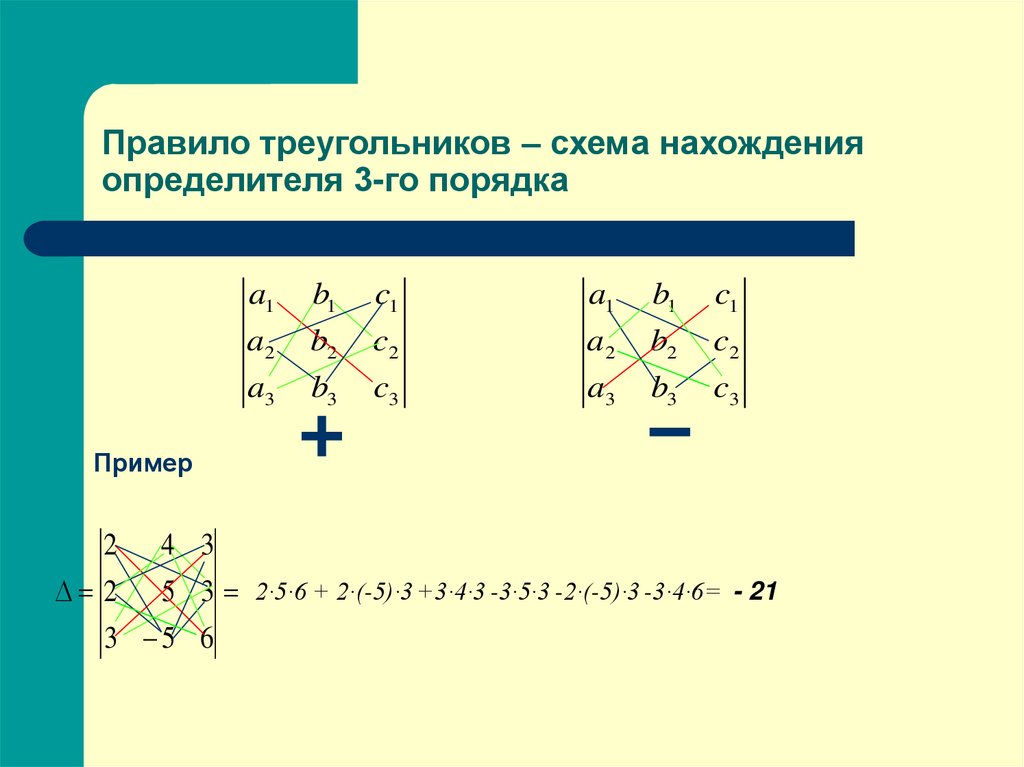
7. Правило треугольников – схема нахождения определителя 3-го порядка
a1b1
c1
a1
b1
c1
a2
b2
c2
a2
b2
c2
a3
b3
c3
a3
b3
c3
Пример
2
2
4 3
5 3 2∙5∙6 + 2∙(-5)∙3 +3∙4∙3 -3∙5∙3 -2∙(-5)∙3 -3∙4∙6= - 21
3 5 6
8. Правило Саррюса- схема нахождения определителя 3-го порядка
a1 b1 c1a1 b1
a2 b2 c2 a2 b2
a3 b3 c3 a3 b3
a1 b2 c3+ b1 c2 a3 + c1 a2 b3 - c1 b2 a3 - a1 c2 b3 - b1 a2 c3
Пример
2
4 3
2
4
2
5 3
2
5 2∙5∙6 + 4∙3∙3+3∙2∙(-5) -3∙5∙3 -2∙3∙(-5) -4∙3∙6= - 21
3 5 6
3 5
9. Свойства определителей
1. Значение определителя не изменится, если строки определителязаменить столбцами, а столбцы – соответствующими строками.
2. Общий множитель элементов какой-нибудь строки (или столбца)
может быть вынесен за знак определителя.
3. Если элементы одной строки (столбца) определителя
соответственно равны элементам другой строки (столбца), то
определитель равен нулю.
4. При перестановке двух строк (столбцов) определитель меняет
знак на противоположный.
5. Определитель не изменится, если к элементам одной строки
(столбца) прибавить соответственные элементы другой строки
(столбца), умноженные на одно и тоже число.
6. Если все элементы какой-нибудь строки (столбца) равны нулю, то
определитель равен нулю.
10. Пример
Вычислить определитель 3-го порядка2 3 1
4 3 3
4 3 3
Так как элементы 2-ой и 3-ей строки одинаковы, то
определитель равен 0.
11. Система двух линейных уравнений с тремя неизвестными.
a1 x b1 y c1 z 0a2 x b2 y c2 z 0
Если a1/a2=b1/b2=c1/c2, то система сводится к одному
уравнению (например, первому), из которого одно выражается
через два других, значения которых остаются произвольными.
Если a1/a2=b1/b2=c1/c2 не выполнено, то решения системы
находятся по формулам
x
b1
c1
b2
c2
t,
y
a1
c1
a2
c2
t, z
a1
b1
a2
b2
t.
12. Правило Крамера – метод решения системы линейных уравнений
a1 x b1y c1 z d1a 2 x b2y c 2 z d 2
a x b3y c3 z d 3
3
a1
b1
c1
d1
b1
c1
a2
b2
b2
a3
b3
c2 , x d 2
c3
d3
c2 , y a2 d 2 c2 , z a2 b2 d 2
a3 d 3 c3
c3
a3 b3 d 3
b3
a1
d1
c1
a1
b1
d1
13. Варианты решений
Δ≠0– система имеет единственное решениех х,
у
у
, z
z
- формулы Крамера
Δ=0, Δx≠0, Δу ≠0, Δz ≠0- система не имеет решения
Δ=0, Δx=0, Δу =0, Δz =0-система имеет бесконечное
множество решений
14. Пример: Решить систему линейных уравнений
2 x y 3z 9,8 x 3 y 5 z 13,
2 x 5 y z 5.
15. Система трех однородных линейных уравнений с тремя неизвестными.
Линейное уравнение называется однородным, если его свободныйчлен равен нулю.
Система линейных уравнений называется однородной, если все
входящие в нее уравнения являются линейными однородными
уравнениями.
a1 x b1 y c1 z 0
a2 x b2 y c2 z 0
a x b y c z 0
3
3
3
Если определитель отличен от нуля, то она имеет единственное
решение x=0, y=0, z=0.
В противном случае она имеет бесконечное множество решений
16. Понятие определителя n-го порядка.
Определителем n-го порядка называется числоΔ,образованное
из
n2
чисел
aij(элементов),
расположенных в квадратной таблице из n строк и n
столбцов, следующим образом
a11 ... a1 j ... a1n
a21 ... a2 j ... a2 n
... ... ... ... ...
an1 ... anj ... ann
17.
Минором Мij элемента aij определителя n-гопорядка называется определитель (n-1)-го порядка
который получается путем вычеркивания в исходном
определителе строки и столбца, содержащих элемент
aij.
Алгебраическим дополнением Аij элемента aij
определителя n-го порядка называется его минор,
умноженный на (-1) i+j
Аij=(-1) i+j Мij
18. Теорема Лапласа
Каждый определитель равен сумме произведений элементов любойего строки(столбцов) на их алгебраические дополнения, т.е.
19. Пример: Вычислить определитель, разлагая его по элементам второго столбца
20. Пример: Вычислить определитель 4-го порядка
2 5Пример:
Вычислить определитель 4-го порядка
3
2
5
9
1
1
6
4
2
2
18
7 10
Прибавим к первой строке удвоенную третью, ко второй строке -третью,
умноженную на -2, а к четвертой строке – третью, умноженную на -2:
2 5
1
1
3
2
5
9
1
1
6
4
2
2
18
7 10
Получили преобразованный определитель, который можно разложить по
первому столбцу:
0
17
7
1
0
7
1
5
1
6
4
2
0
30
15
6
17
7
30
7
1
17
5 3 7
15 6
10
1
7
1
1
5
306
5 2
Теперь определитель 3-го порядка можно также разложить по строке
(столбцу) или подсчитать по правилу треугольников, предварительно
вынося за знак определителя общий множитель третьей строки
21. Обобщение формулы Крамера на случай системы n - линейных уравнений.
Обобщение формулы Крамера на случай системы n линейных уравнений.a 11 x1 a 12 x 2 ... a 1n x n b1
a21 x1 a22 x2 ... a2 n xn b2 ;
...............
a x a x ... a x b .
n2 2
nn n
n
n1 1
Из коэффициентов при неизвестных составим определитель, т.е.
det
a11
a12
a21
a22 ... a2 n
.
an1
.
... a1n
...
.
an 2 ... ann
22. Варианты решений
Если для системы уравнений определитель Δ≠0, тосистема имеет единственное решение
x
i
i
, i 1, n
где определитель Δi - полученный из определителя
Δ заменой i-го столбца на столбец свободных
членов.
23. Пример: Решить систему линейных уравнений
Вычислим определитель системы24. Поскольку ∆ ≠ 0, система уравнений может быть решена по формулам Крамера. Найдем определители ∆x1 – ∆x4:
õ1õ2
25.
õ3Таким же образом высчитываем ∆х4 и получаем: ∆х1 = ∆х2 = –∆х3 =
∆х4,
и, следовательно, х1 = х2 = –х3 = х4 = 1.
26. Понятие матрицы. Линейные операции над матрицами
Матрицейразмера
т
х
n
называется
прямоугольная таблица чисел, содержащая т строк и
n столбцов
a11
a21
...
А
ai1
...
a
m1
a12
... a1 j
a22
... a2 j
...
...
...
ai 2
...
aij
...
...
...
am 2 ... amj
... a1n
... a2 n
... ...
... ain
... ...
... amn
Наряду
с
круглыми
скобками используются
и другие обозначения
матрицы: [ ], || ||.
или, в сокращенной записи, А=(аij); i=1, 2, ..., m;
j = 1, 2, ..., n.
27. Виды матриц
Две матрицы А и В одного размера называются равными,если они совпадают поэлементно, т.е. aij = bij для любых
i=1, 2, ..., m; j = 1, 2, ..., n.
Матрица называется квадратной n-го порядка, если число
ее строк равно числу столбцов и равно n
Матрица, состоящая из одной строки, называется
матрицей-строкой, а из одного столбца-матрицей-столбцом
28. Виды матриц
a11Матрица AT a12
.
a
1n
a 21
a 22
.
a 2n
... a m1
... a m 2
...
.
... a mn
получающаяся из матрицы A
заменой строк столбцами (и наоборот), называется
транспонированной (по отношению к матрице матрицей.
Матрица называется симметрической матрицей, если AT= A
кососимметрической, если AT= -A
29. Линейные операции над матрицами.
Умножением матрицы на число k называется матрица,каждый элемент которой умножен на это число.
Суммой двух матриц одинаковых размеров называется
матрица, элементы которой равны суммам элементов
исходных матриц, расположенных на соответствующих
местах.
Разность двух матриц одинаковых размеров определяется
через предыдущие операции: А - В=А+(-1) В.
Умножением матрицы на матрицу называется матрица,
каждый элемент которой равен сумме произведения
элементов i -й строки первой матрицы на
соответствующие элементы j-го столбца второй
матрицы.
30. Обратная матрица
Квадратная матрица А-1 определитель которой detA≠0,называется неособенной или невырожденной матрицей. В
противном случае она называется вырожденной или особенной.
Квадратная матрица называется обратной к квадратной
матрице, если выполняется равенство
1
1
AА А А Е
31. Теорема (необходимое и достаточное условие существования обратной матрицы).
Обратнаяматрица
существует
(и
единственна) тогда и только тогда, когда исходная
матрица невырожденная
A11
1 A12
1
А
А .
A
1n
An1
... An 2
... .
... Ann
A21 ...
A22
.
A2 n
32. Пример: Найти матрицу, обратную к матрице
1A 3
0
2
2
1
0
1
2
33. Пример: Найти матрицу, обратную матрице А=
1 4 34 2 1
Найти матрицу, обратную матрице А=
3 6 3
Пример:
Найдем определитель исходной матрицы:
1
4
∆А= 4
2
3
6
3
1 0
3
Так как ∆А = 0, то данная матрица не
является вырожденной, и для нее нельзя
составить обратную матрицу
34. Решение системы линейных уравнений методом обратной матрицы
35. Пример: Решить систему уравнений
x1 x3 2,x1 x2 x3 6,
x 3 x 5.
3
2
36. Ранг матрицы.
Пусть в матрицеa11
a
A 21
.
a
m1
a12
...
a22
...
.
.
am 2
...
a1n
a2 n
.
amn
произвольно выделено k строк и k столбцов. Элементы, стоящие
на пересечении выделенных строк и столбцов, образуют
квадратную матрицу порядка k, определитель, которой называется
минором k-го порядка матрицы.
Максимальный порядок r отличных от нуля миноров матрицы,
называется рангом матрицы и обозначается r(A). Любой минор
порядка r, отличный от нуля, называется базисным минором.
37. Методы вычисления ранга матрицы - метод окаймляющих миноров
Пусть в матрице найден минор k-го порядка,отличный от нуля. Рассмотрим лишь те миноры
(k+1)-го порядка, которые содержат в себе
(окаймляют) минор , если все они равны нулю, то
ранг минора равен k. В противном случае среди
окаймляющих миноров найдется ненулевой минор
(k+1)-го порядка, и вся процедура повторяется.
38. Пример: Найти ранг матрицы
10
A
2
2
2
1
1
1
5
1
4
2
4
3
.
11
8
39. Совместность систем уравнений. Теорема Кронеккера-Капелли.
40. Пример: Установить совместимость системы
2 x1 x2 x3 3 x4 2,4 x x 7 x 1,
1
3
4
2 x2 3 x3 x4 1,
2 x1 3 x2 4 x3 2 x4 3.
41. Литература
Основная:Щипачев В.С. Высшая математика. Учебн. Для вузов. 3-е изд., стер.-М., Высшая школа. 1996-479 с.
Щипачев В.С. Задачник по высшей математике. Учебн. Для вузов. 2-е изд., испр.-М., Высшая школа
1998-304с.
Рябушко А.П. Сборник индивидуальных заданий по высшей математике., Минск «Высшая школа.»,
1991г., часть 1, 2, 3.
Данко П.Е., Попов А.Г., Кожевников Т.Я., Высшая математика в упражнениях и задачах, ч.1,2,
М.В.Ш., 1996 г.
Мантуров О.В., Матвеев Н.М. Курс высшей математики. Москва, Высшая школа., 1, 2, 3 т., 1991,
448с.
Кудрявцев Л.Д. Курс математического анализа., М., 1988, 1989, т.1-3
Гурман В. Е. Руководство к решению задач по теории вероятностей и математической статистики.
Высшая школа. 1979 г.
Ильин В. А., Позняк Э. Г. Аналитическая геометрия. Н., 1988 – 223 с.
Владимиров В. С., Жариков В. П. Уравнение математической физики. М. 2003 г.
Чудесенко В. Ф. Сборник заданий по специальным курсам высшей математики. М., В. Ш., 1985 –
105 с.
Дополнительная:
Каплан И. А. Практические занятия по высшей математике. Харьков, 1980 г.
Пискунов Н. П. Дифференциальное и интегральное исчисление по математике для вузов. М., 1970
г., 1985 г., т. 1, 2
Бугров Я. С., Никольский С. М. Высшая математика. Дифференциальное и интегральное
исчисление. М., 1980 г., 1984 г.
Бугров Я. С., Никольский С. М. Высшая математика. Дифференциальные уравнения. Кратные
интегралы. Ряды. Функции комплексного переменного. М., 1981 г., 1985 г.








































 mathematics
mathematics








