Similar presentations:
Высшая математика. Лекция 2
1. Высшая математика Лекция 2 Группы LT 10-24, KA 9-24
СЛАУ2. Линейная алгебра
Системы из n линейных уравнений с nнеизвестными.
Метод Гаусса решения систем линейных
уравнений
Ранг матрицы
Исследование систем линейных уравнений
Однородные системы линейных уравнений
3. Системы из n линейных уравнений с n неизвестными
Рассмотрим общую квадратную систему линейных уравнений:a11x1 a12 x 2 a1n x n b1
a21x1 a22 x 2 a2n x n b2
an1x1 an2 x 2 ann x n bn
Система линейных уравнений называется совместной, если она
имеет решение и несовместной, если она не имеет решений.
Совместная система называется определенной, если она имеет
единственное решение и неопределенной, если она имеет
бесконечное множество решений.
Система называется однородной, если b1 b2 bn 0
Однородная система совместна, так как всегда имеет нулевое
решение.
4. Системы из n линейных уравнений с n неизвестными
Для сокращения выкладок запишем систему из трех уравнений стремя неизвестными:
a11x1 a12 x 2 a13 x 3 b1
a21x1 a22 x 2 a23 x 3 b2
a x a x a x b
33 3
3
31 1 32 2
a11 a12 a13
a 21 a 22 a 23
a31 a32 a33
Вспомогательные определители получаются из главного
определителя, если заменить соответствующий столбец столбцом
свободных членов:
b1 a12 a13
a11 b1 a13
a11 a12 b1
1 b 2 a 22 a 23
2 a 21 b 2 a 23
3 a 21 a 22 b 2
b3 a32 a33
a31 b3 a33
a31 a32 b3
5. Системы из n линейных уравнений с n неизвестными
По величине главного и вспомогательных определителей можносудить о характере системы:
Если
0 то система совместна и определенна.
Если 0, 1 2 3 0
неопределенна.
то система совместна и
Если 0, но 1 0 или 2 0 или 3 0 то
система несовместна.
В общем случае будем иметь n +1 определителей n – ого порядка
, 1, 2 , 3 , , n 2 , n 1, n
и, если 0 , то решение системы находится по формулам
Крамера:
1
x1 ;
2
x2
;
n
xn
6. Метод Гаусса решения систем линейных уравнений
Рассмотрим задачу решения системы линейных уравненийразмерностью (m x n). Запишем систему в матричном виде: A X B
Если закрепить раз и
a11 a12 a13 a1n x1 b1 навсегда нумерацию
a21 a22 a23 a2n x 2 b2 неизвестных, то можно
неизвестные в
опустить
системы и
записи
a a a a x b записать ее в виде
mn n
m матрицы, отделяя
m1 m 2 m3
b1
a11 a12 a13 a1n
a21 a22 a23 a2 n b2
B A B
a a a a b
m
mn
m1 m 2 m 3
столбец свободных
членов вертикальной
чертой.
Расширенная матрица
системы
7. Метод Гаусса решения систем линейных уравнений
Следующие действия над расширенной матрицей системыназываются элементарными преобразованиями.
Умножение или деление элементов строк на одно и то же
число, не равное нулю
Перестановка местами двух строк
Прибавление к элементам строки элементов другой строки,
умноженных на произвольный множитель.
Конечной целью элементарных преобразований является
получение верхнетреугольной матрицы, у которой все элементы,
стоящие под главной диагональю равны нулю. Преобразования
стараются производить так, чтобы на главной диагонали
появлялись единицы.
a11 a12
a 21 a 22
a
31 a32
a13
a 23
a33
b1
1 c 12
b2 0 1
0 0
b3
c 13
c 23
1
d1
d2
d3
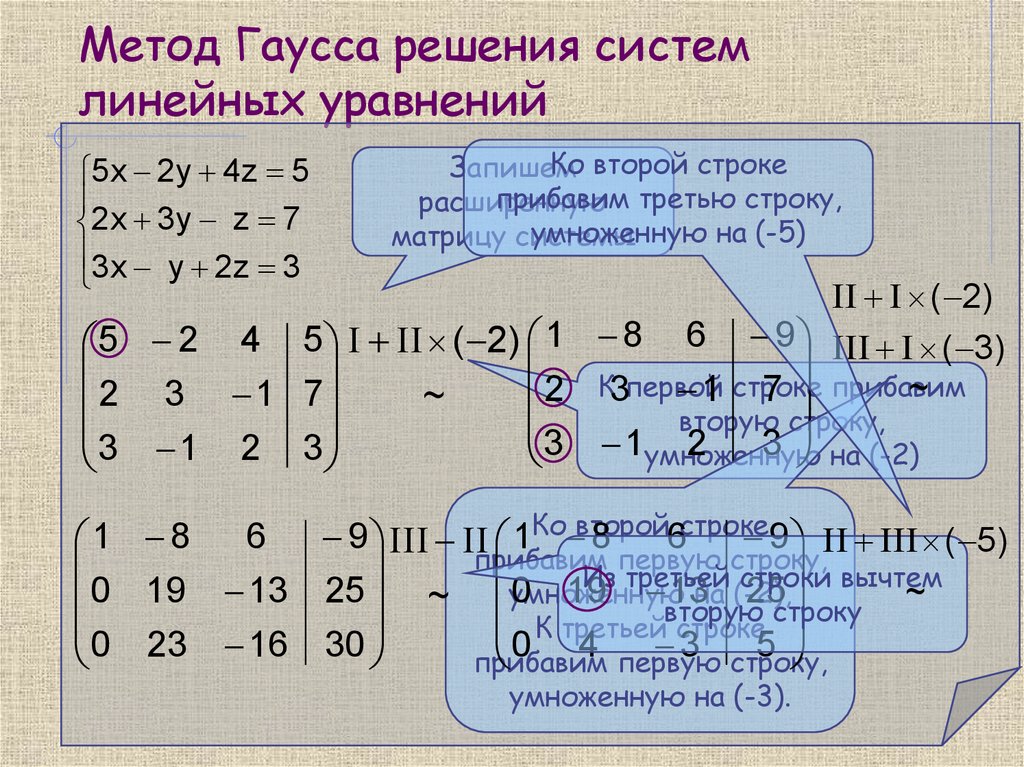
8. Метод Гаусса решения систем линейных уравнений
5x 2y 4z 52x 3y z 7
3x y 2z 3
Ко второй строке
Запишем
прибавим третью строку,
расширенную
умноженную на (-5)
матрицу системы
( 2)
5 2 4 5 ( 2) 1 8 6 9 ( 3)
~
1 строке
7 прибавим
2 К3первой
~
2 3 1 7
строку,
3 1 вторую
3 1 2 3
2
3
умноженную
на (-2)
6
9 1Ко второй
8
6строке
9 ( 5)
1 8
прибавим
первую
строку,
вычтем
Из третьей строки
0 19 13на (-2),
25
~
0 19 13 25 ~ умноженную
вторую строку
строке
0 23 16 30
0 К третьей
4 первую
3 строку,
5
прибавим
умноженную на (-3).
9. Метод Гаусса решения систем линейных уравнений
( 1): 5
~
1 8 6 9 4 1 8 6 9
0
~
0 1 2
0 1 2 0
строке
0 4 3 5
0 К0третьей
прибавим
5
5
вторую строку,
умноженную на 4
1 8 6 9
Вторую строку умножим
на (-1), третью
строку
Восстановим
систему:
0 1 2 0
разделим на 5
0 0
1
1
x 8y 6z 9
x 9 8y 6z
x 9 16 6 1
y
2
z
0
y 2
y 2z 2
z 1
z 1
z
1
x 1 y 2
z 1
10. Ранг матрицы
Рассмотрим прямоугольную матрицу размерностью (m x n).a11 a12
a 21 a 22
a
a32
31
am1 am 2
a13
a 23
a33
am 3
a1n
aa1111 a12 aa131n
a 2n
a1112 aa121n
22aa 3121 a3222 aa233n
M33M
a3n M
a2132 aa223n
aam311 aam322 a33mn
amn
Выделим в этой матрице произвольное число k строк и k столбцов.
Элементы матрицы А, стоящие на пересечении выделенных строк
и столбцов, образуют определитель k - того порядка.
Минором k-того порядка матрицы А называют определитель,
полученный из А выделением произвольных k строк и k столбцов.
11. Ранг матрицы
Рангом матрицы называется наибольший порядок отличного отнуля минора этой матрицы.
2 3 4 5
A 0 2 3 1
0 2 2 4
Матрица А имеет 4 минора 3 - его порядка,
например:
18 миноров 2 - го порядка, например:
2 3 4
0 2 3 20
0 2 2
2 3
4
0 2
12 миноров 1 - го порядка – сами элементы.
Наибольший порядок отличного от нуля минора
этой матрицы равен 3, поэтому: r ( A ) 3
12. Ранг матрицы
Определитель, порядок которого равен рангу матрицы, называетсябазисным минором. Он может быть не единственным.
Можно показать, что эквивалентные преобразования не меняют
ранга матрицы. Поэтому, когда требуется вычислить ранг матрицы,
ее приводят к треугольному виду.
Ранг матрицы равен числу ненулевых строк матрицы,
приведенной к треугольному виду
1 3 2 1 3 2 ( 2) 1 3 2
A 0 5 4 ~ 0 5 4
0 5 4
~
1 7 6
0 0 0
0 10 8
r( A ) 2
13. Исследование систем линейных уравнений
Теорема Кронекера - Капелли.Для того, чтобы система линейных алгебраических уравнений
была совместна (имела решение ), необходимо и достаточно,
чтобы ранг расширенной матрицы
системы равнялся рангу
матрицы коэффициентов: r (B) r ( A )
Если r (B) r( A ) n (числу неизвестных), то система
совместна и определенна (имеет единственное решение).
Если r(B) r( A ) n ,то система совместна и неопределенна
(имеет бесконечное множество решений).
Если r (B) r ( A ) ,то система несовместна (не имеет решений).
При решении систем линейных алгебраических уравнений нет
необходимости заранее вычислять ранги основной и расширенной
матриц. Их определение производится автоматически при
выполнении метода исключения Гаусса.
14. Исследование систем линейных уравнений
2x1 2x 2 2x 3 4x1 x 2 x 3 0
3 x1 3 x 2 x 3 2
x1 x 2 3 x 3 2
1 1 1 2 ( 3) 1
0
1 1 1 0 V
~
0
3 3 1 2
0
1 1 3 2
2 2 2 4
:2
1 1 1 0
3 3 1 2 ~
1 1 3 2
1 1
2
0 2 2
0 4 4
0 4
4
: ( 2)
: ( 4)
V : 4
~
15. Исследование систем линейных уравнений
10
0
0
1
0
0
0
1
1
1
1
2 1
1 V 0
~
0
1
0
1
r(B) r( A ) 2
1
0
0
0
1
1
0
0
2
1
0
0
система совместна
n 3 - число неизвестных
r(B) n система неопределенна
n r 3 2 1 - число свободных переменных
Восстановим систему:
Пусть x 2 t.
x1 1 t
x1 2 t x 3 1 t
x1 t x 3 2
x2 t
x3 1
x3 1
x 1
3
16. Исследование систем линейных уравнений
( 2)1 2 4 1
2 1 5 1
~
1 1 1 3
1 2 4 1 1 2 4 1
~
0 3 3 3
0 3 3 3
0 3 3
0 0
2
0
5
r(B) 3
r( A ) 2
r(B) r( A ) система несовместна
x 2y 4z 1
2x y 5z 1
x y z 3
17. Однородные системы линейных уравнений
Система линейных уравнений называется однородной, если всесвободные члены ее равны нулю.
a11x1 a12 x 2 a1n x n 0
a21x1 a22 x 2 a2n x n 0
am1x1 am2 x 2 amn x n 0
Однородная система всегда имеет решение:
x1 0
x 2 0 xn 0
Это решение называется тривиальным. Оно является
единственным решением системы в случае, когда r( A ) n
Если r( A ) n , то система имеет бесконечное множество
решений.
18. Однородные системы линейных уравнений
Пусть: r ( A ) r nТогда система имеет r базисных переменных и n – r свободных
переменных.
Общее решение системы запишется в виде:
x1( t1,..., t n r )
...
x r ( t1,..., t n r )
X
t1
...
t
n r
Базисные переменные,
зависящие от свободных
переменных
Значения свободных
переменных
t1 xr 1; t 2 xr 2 ; tn r xn
19. Однородные системы линейных уравнений
Выберем n - r частных решений однородной системы, полученныхиз общего решения следующим образом: полагаем одно из
значений свободных переменных равным 1, а остальные равными
0 :
x1(1,0,..., 0)
x1(0,0,...,1)
x1(0,1,..., 0)
x r (0,0,...,1)
x r (1,0,..., 0)
x r (0,1,..., 0)
0
1
0
X
X1
X2
n r
0
0
1
1
0
0
Эти решения образуют фундаментальную систему решений
однородной системы (ФСР).
20. Однородные системы линейных уравнений
( 2)1 1 5 7 ( 3)
~
1
2 1 4
3 2 1 6
Найти фундаментальную систему решений:
x1 x 2 5 x 3 7 x 4 0
2x1 x 2 4 x 3 x 4 0
3 x 2x x 6 x 0
2
3
4
1
1 1 5 7 1 1 5 7 ( 1)
~
~
0 1 14 15
0 1 14 15
0 0
0 1 14 15
0
0
1 1 5 7
0 1 14 15
r( A ) 2
n 4
n r 4 2 2 - число свободных переменных
21. Однородные системы линейных уравнений
Обозначим:x 3 t1
x4 t2
(в качестве свободных переменных обычно берут те,
которые имеют 0 на главной диагонали)
x 1 x 2 5t 1 7t 2
x 1 x 2 5t 1 7t 2 0
x 2 14t1 15t 2
x 2 14t1 15t 2 0
x1 14t1 15t 2 5t1 7t 2 11t1 12t 2 Фундаментальная
система решений
x 2 14t1 15t 2
11t1 12t 2
14t1 15t 2
X
t1
t
2
11 решение
12
Общее
15
14
X2
X1
0
1
1
0
22. Метод Жордана-Гаусса для решения СЛАУ
Метод Жордана-Гаусса для решения СЛАУОсновные понятия
Произвольный способ выбора
разрешающих элементов
Выбор разрешающих элементов на
главной диагонали матрицы системы
23. Основные понятия
Основные понятияОпределение 1
Метод Жордана-Гаусса — один из
методов, предназначенный для решения
систем линейных алгебраических
уравнений.
Этот метод является модификацией
метода Гаусса — в отличие от исходного
(метода Гаусса) метод Жордана-Гаусса
позволяет решить СЛАУ в один этап (без
использования прямого и обратного
ходов).






















 mathematics
mathematics








