Similar presentations:
Сдвиг графика квадратичной функции у=ах2 вдоль осей координат
1.
Сдвиг графикаквадратичной функции
у=ах2 вдоль осей координат
9 класс
г. Воронеж 2019
2. Цели урока:
научиться строить графики функции
у=ах2+q, у=а(х+p)2 из графика у=ах2;
обобщить выводы для функции
вида
у=а(х+p)2+q.
3.
У9
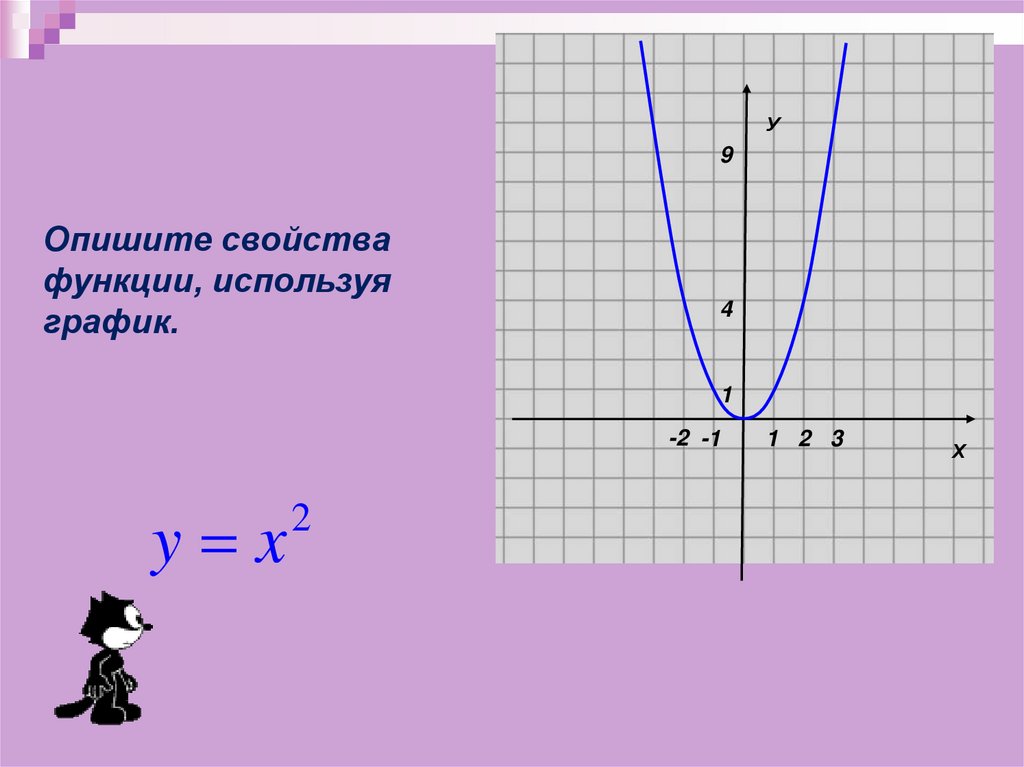
Опишите свойства
функции, используя
график.
4
1
-2 -1
y x
2
1 2 3
Х
4.
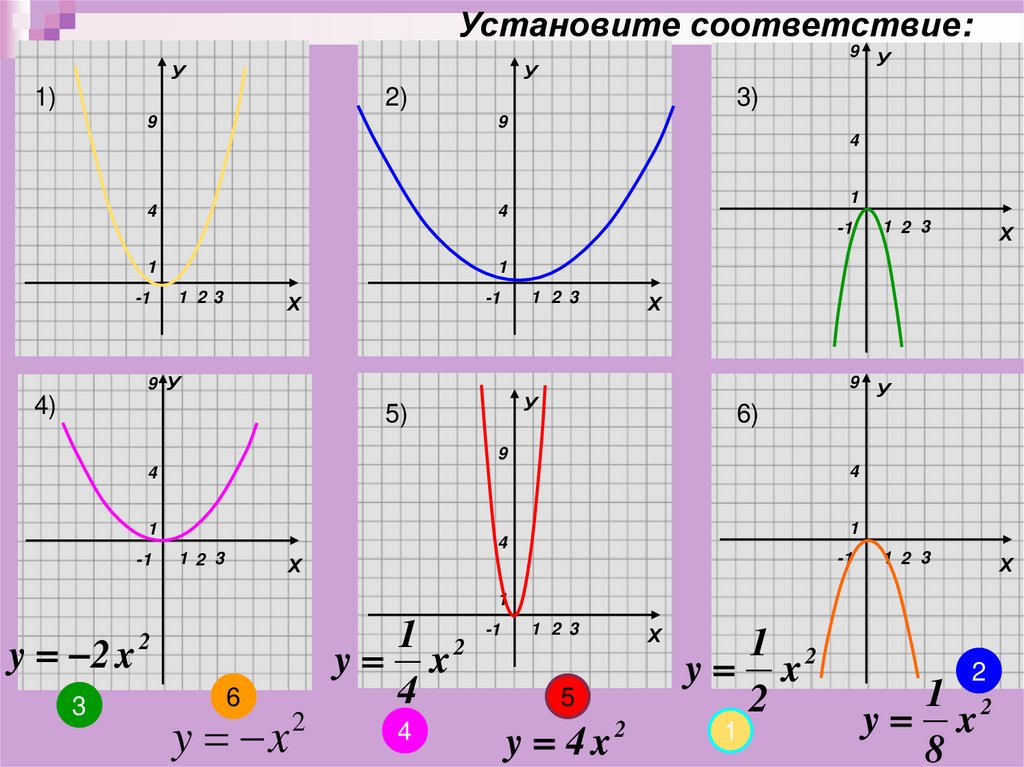
Установите соответствие:9
У
У
1)
2)
9
У
3)
9
4
4
1
4
-1
1
-1
1 2 3
Х
1
1 2 3
1 2 3
-1
Х
9 У
Х
9
4)
У
5)
У
6)
9
4
4
1
-1
1
4
1 2 3
-1
Х
1 2 3
Х
1
y 2 x
3
1 2
y x
4
2
6
y x
2
4
-1
1 2 3
5
y 4 x2
Х
1 2
y x
2
1
2
1 2
y x
8
5.
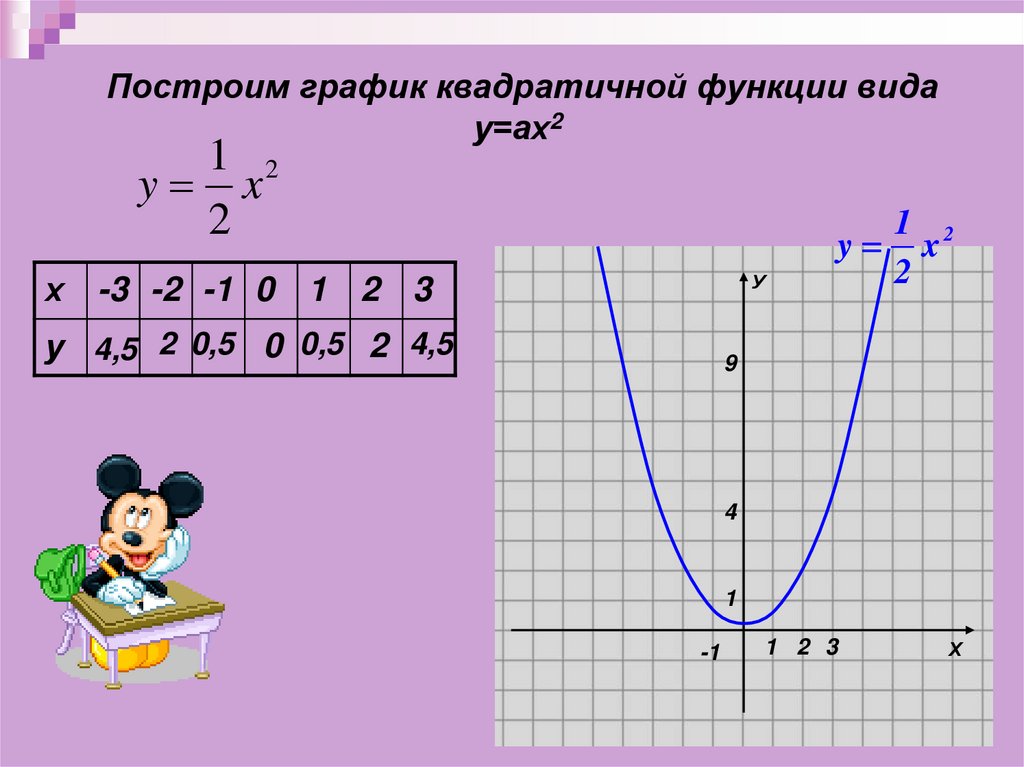
Построим график квадратичной функции видау=ах2
1 2
y x
2
х -3 -2 -1 0 1 2 3
У
у 4,5 2 0,5 0 0,5 2 4,5
1 2
y x
2
9
4
1
-1
1 2 3
Х
6.
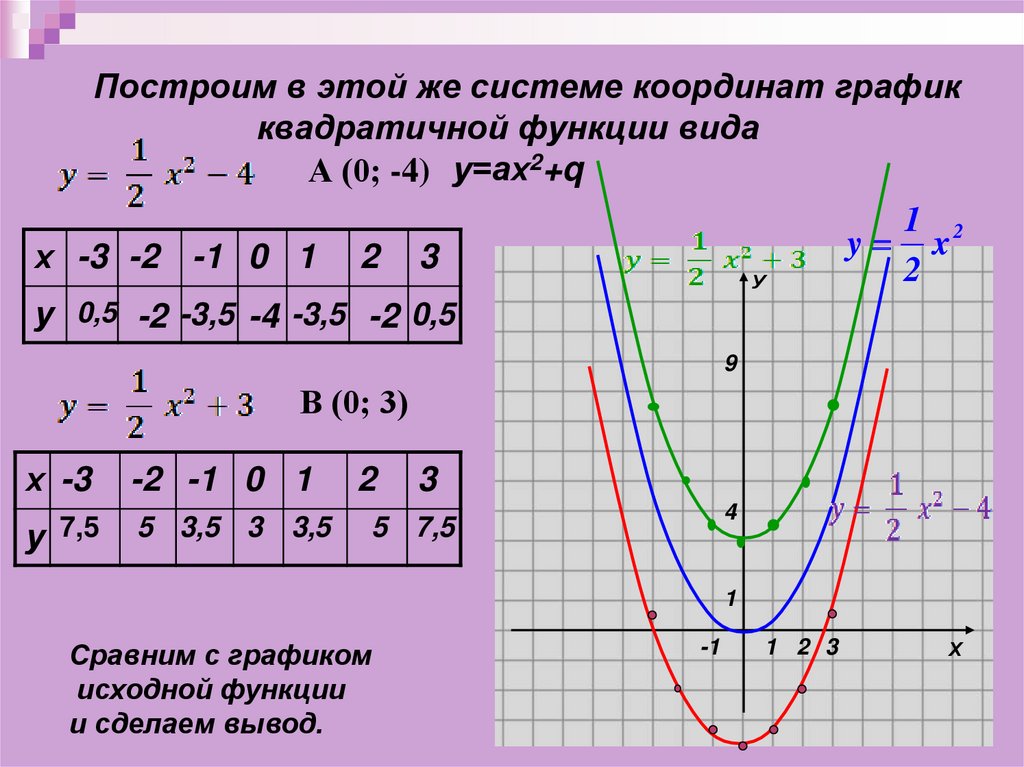
Построим в этой же системе координат графикквадратичной функции вида
А (0; -4) у=ах2+q
1 2
y x
х -3 -2 -1 0 1 2 3
2
У
у 0,5 -2 -3,5 -4 -3,5 -2 0,5
9
В (0; 3)
х -3
-2 -1 0 1
у 7,5
5 3,5 3 3,5
2
3
4
5 7,5
1
Сравним с графиком
исходной функции
и сделаем вывод.
-1
1 2 3
Х
7.
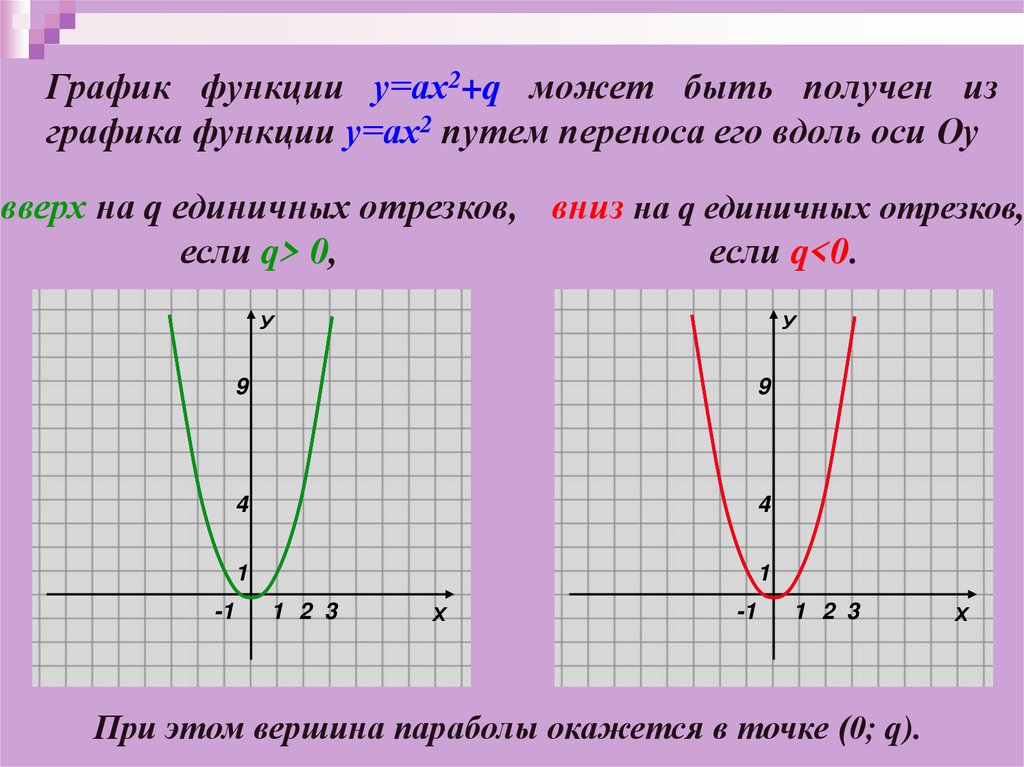
График функции у=ах2+q может быть получен изграфика функции у=ах2 путем переноса его вдоль оси Оу
вверх на q единичных отрезков, вниз на q единичных отрезков,
если q> 0,
если q<0.
У
-1
У
9
9
4
4
1
1
1 2 3
Х
-1
1 2 3
При этом вершина параболы окажется в точке (0; q).
Х
8.
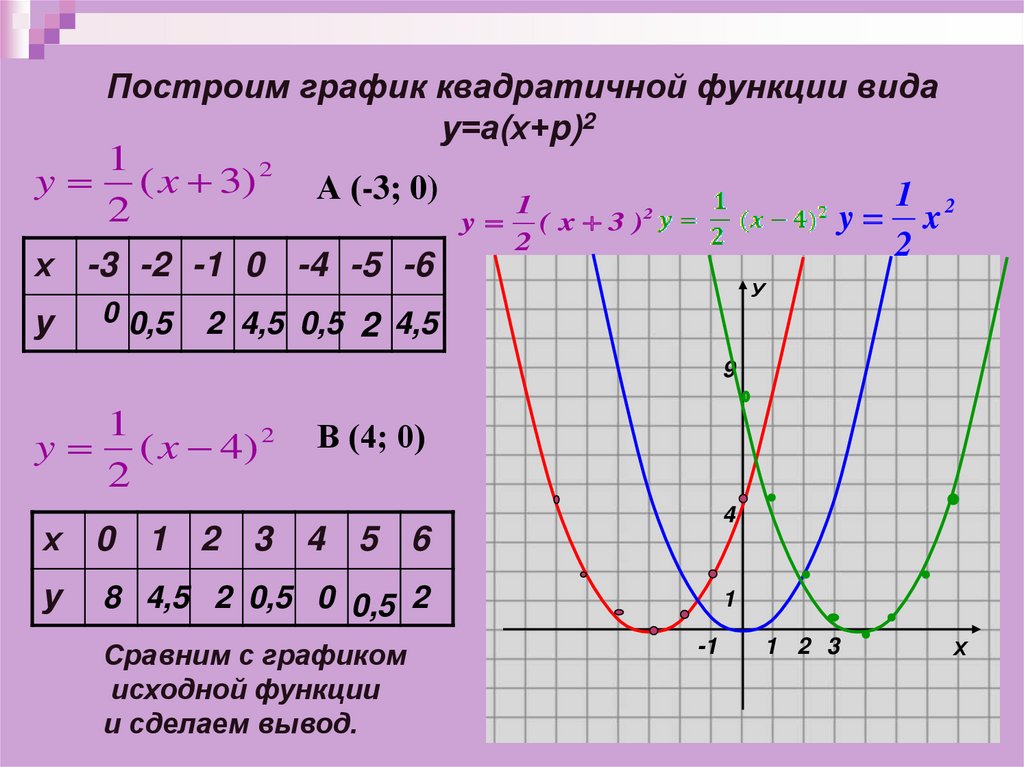
Построим график квадратичной функции видау=а(х+p)2
1
y ( x 3) 2
2
А (-3; 0)
х -3 -2 -1 0 -4 -5 -6
у
0 0,5
1 2
y x
2
1
y ( x 3 )2
2
У
2 4,5 0,5 2 4,5
9
1
y ( x 4) 2
2
В (4; 0)
4
х 0 1 2 3 4 5 6
у
8 4,5 2 0,5 0 0,5 2
Сравним с графиком
исходной функции
и сделаем вывод.
1
-1
1 2 3
Х
9.
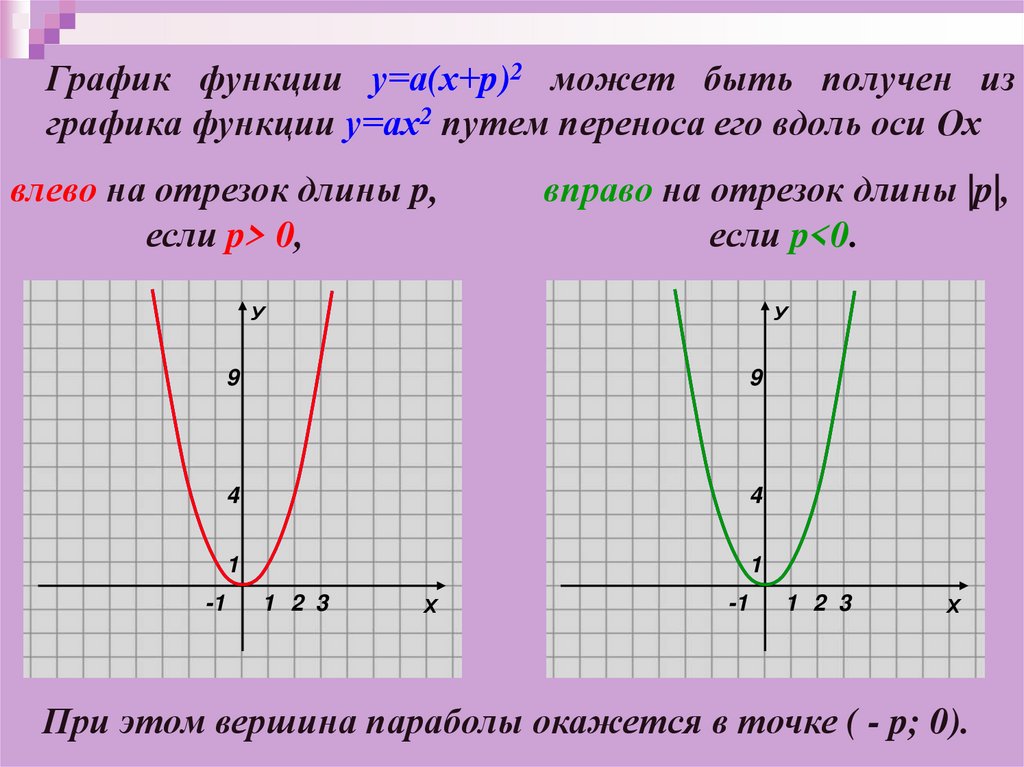
График функции у=а(х+p)2 может быть получен изграфика функции у=ах2 путем переноса его вдоль оси Ох
влево на отрезок длины p,
если p> 0,
вправо на отрезок длины |p|,
если p<0.
У
-1
У
9
9
4
4
1
1
1 2 3
Х
-1
1 2 3
Х
При этом вершина параболы окажется в точке ( - p; 0).
10.
График функции у=а(х+p)2+q может быть получениз графика функции у=ах2
с помощью двух
параллельных переносов:
вдоль оси Оу на |q| единиц – вверх или вниз в
зависимости от знака числа q,
и вдоль оси Ох на |p| единиц – влево или вправо в
зависимости от знака числа p.
Вершиной параболы у=а(х+p)2+q будет точка (- p; q ).
11.
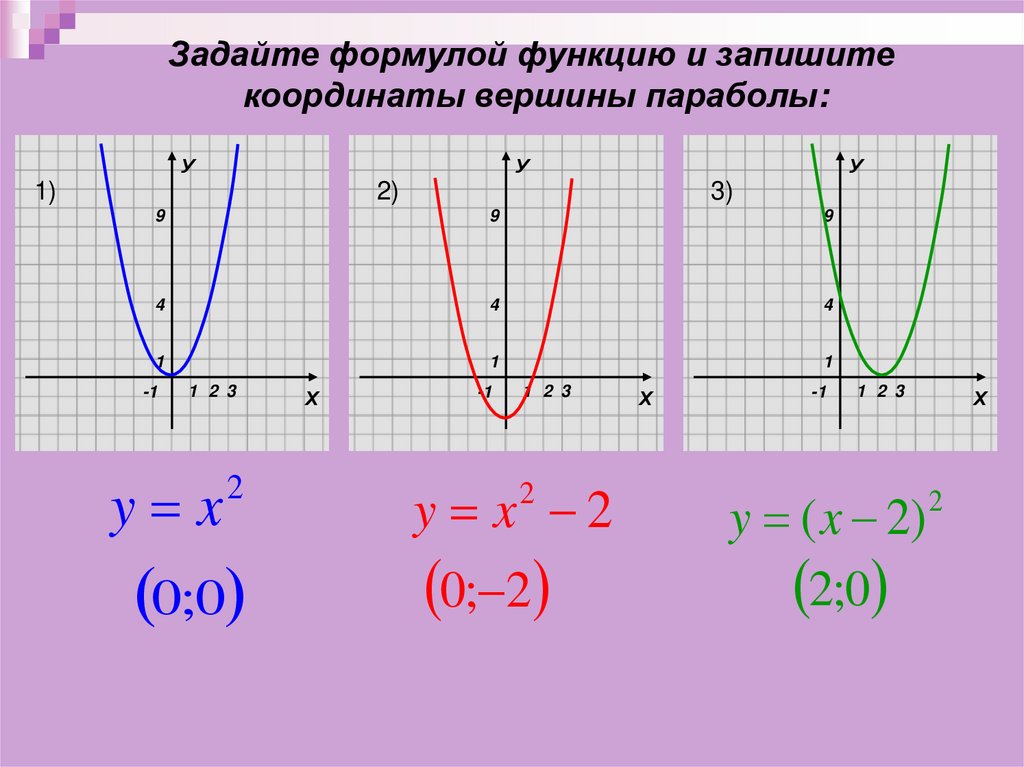
Задайте формулой функцию и запишитекоординаты вершины параболы:
У
У
1)
У
2)
3)
9
9
9
4
4
4
1
1
1
-1
1 2 3
y x
2
0;0
Х
-1
1 2 3
y x 2
0; 2
2
Х
-1
1 2 3
y ( x 2)
2;0
Х
2
12.
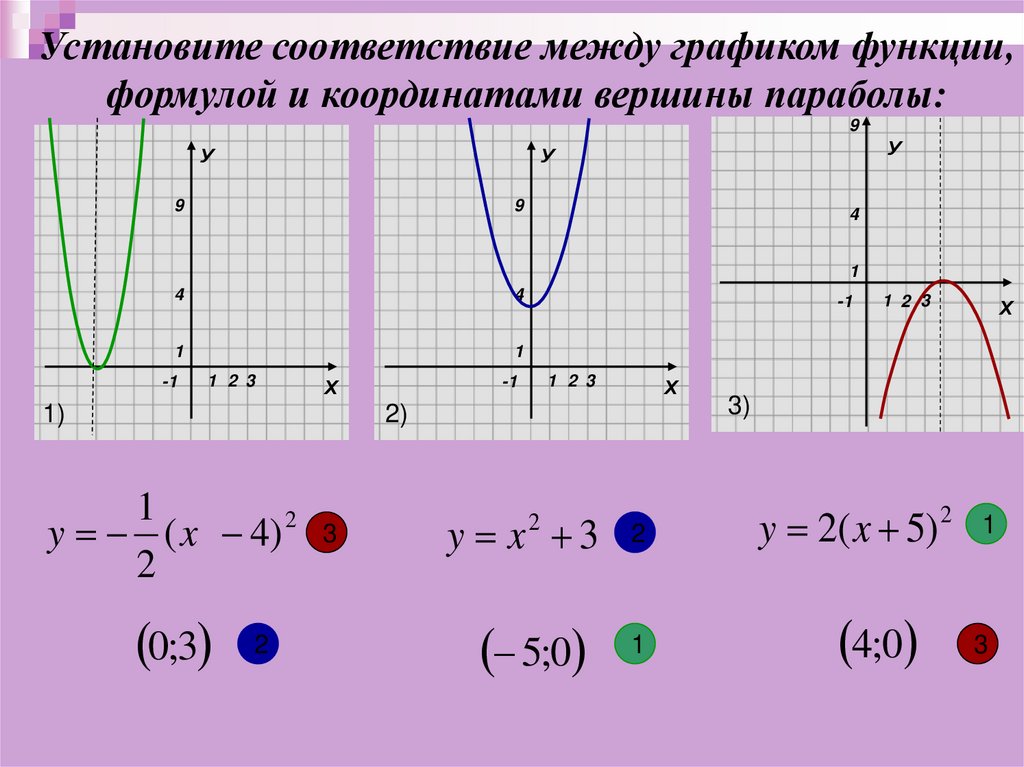
Установите соответствие между графиком функции,формулой и координатами вершины параболы:
9
У
У
У
9
9
4
1
4
4
1
1
-1
1 2 3
1 2 3
-1
Х
1)
-1
Х
2)
1
y ( x 4) 2
2
0;3
2
3
y x 3
2
2
5;0
1
1 2 3
Х
3)
y 2( x 5)
4;0
2
1
3
13.
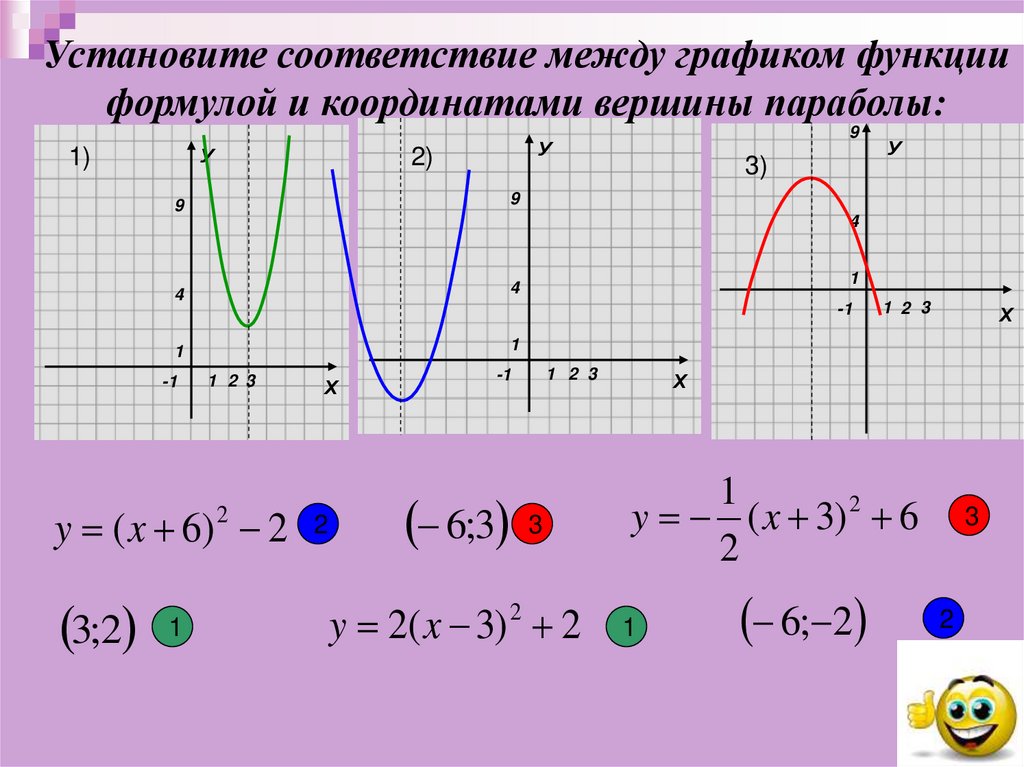
Установите соответствие между графиком функцииформулой и координатами вершины параболы:
У
1)
9
У
2)
3)
У
9
9
4
-1
1 2 3
y ( x 6) 2
2
3;2
1
1 2 3
Х
1
1
-1
1
4
4
Х
2
1 2 3
-1
6;3
3
y 2( x 3) 2
2
Х
1
2
y ( x 3) 6
2
1
6; 2
3
2
14.
Учебник № 106, 109, 111.15.
Итоги урока- Как из параболы y ax 2
получить параболу
y аx 2 q ?
2
- Как из параболы
y ax
получить параболу y a( x p) 2 ?
y ax
- Как из параболы
получить параболу у=а(х+p)2+q
2
16.
Домашнее задание.П. 6 , № 107 (а, б), 108 (в, г), 110, 116
17.
Молодцы.Спасибо.






 mathematics
mathematics








