Similar presentations:
Квадратичная функция у = ах2 + bx + c
1.
7 КЛАСС. АЛГЕБРА.Ш.А. АЛИМОВ
Квадратичная функция
у = ах2 + bx + c
Савченко Е.М.
МОУ гимназия №1, г. Полярные Зори, Мурманская обл.
2.
y=2
ax +bx
+c
a, b, c числа
а 0
Если а=0, то y=bx+c
это линейная функция
3.
b = 0, c = 0y=
у
2
x
0
х - 3 - 2 -1 0 1 2 3
у 9 4 1 0 1 4 9
1
х
4.
y0
y
x
0
1
0
1
2
2
-2
x
: xy 0(;
Rx)
y( y(()xy:))y
ED
5.
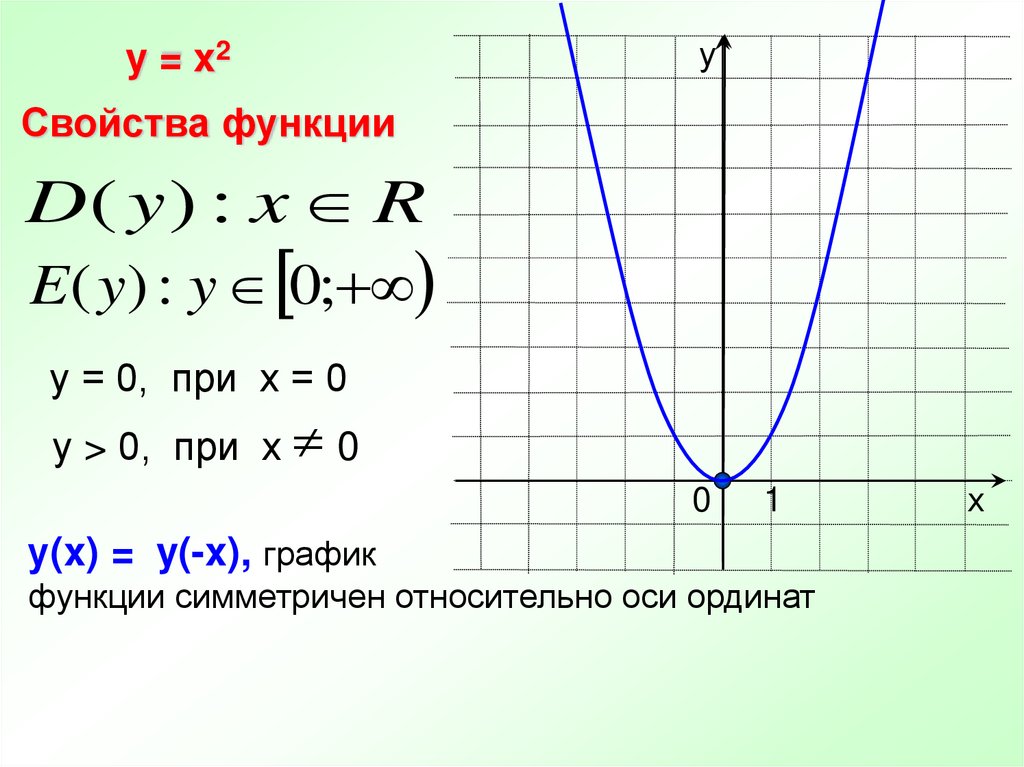
y = x2у
Свойства функции
D( y ) : x R
E( y) : y 0;
у = 0, при х = 0
у > 0, при х 0
0
1
у(x) = y(-x), график
функции симметричен относительно оси ординат
х
6.
y x2
;0
y
0;
-1 0 1 2
x
7.
Свойства функцииу
х<0
у2 у1
x2 > x1, то у2 < y1
Функция убывает
при х < 0
у1 у2
х>0
х1
х2 0
1 х1
х2
х
x2 > x1, то у2 > y1
Функция возрастает
при х > 0
Большему значению аргумента
соответствует
меньшее значение
большее
значение функции
функции
8.
Парабола обладает многимиинтересными свойствами,
которые широко используются
в технике. Например, на оси
симметрии параболы есть
точка, которую называют
фокусом параболы. Если в
этой точке находится источник
света, то все отраженные от
параболы лучи идут
параллельно. Это свойство
используется при
изготовлении прожекторов,
локаторов и других приборов.
Фокусом параболы у = х2
является точка
1
0;
4
у
х
1
9.
у№ 586
х = 0,8
у 0,8
х = 1,5
у 2,6
х = 1,9
у 3,7
х = -2,3
у 6
х = -1,5
у 2,6
-3 -2 -1 0
1 2 3
х
10.
у№ 586
у=2
х1 1,4
у=3
х 1,7
у = 4,5
х 2,1
у = 6,5 х 2,5
-3 -2 -1 0
1 2 3
х
11.
№ 592Верно ли утверждение,
что функция у = х2
возрастает:
у
14
12
1) на отрезке [ 1; 4]
10
2) на интервале (2; 5)
8
3) на промежутке х >3
6
4) на отрезке [–3; 4]
4
2
-3 -2 -1 0
1 2 3 4
х
12.
№ 593На одной координатной
плоскости построена
парабола у = х2 и
прямая у = 3.
При каких значениях х
точки параболы лежат
выше прямой?
у
14
12
10
8
6
х ( ; 3 ) ( 3; )
4
у=3
ниже прямой?
2
х ( 3; 3 )
-3 -2 -1 0
1 2 3 4
х
13.
у№ 594
14
При каких х значения
функции у = х2
12
1)
больше 9;
y>9
х ( ; 3) (3; )
10
у=9
8
6
4
2
-3 -2 -1 0
1 2 3 4
х
14.
у№ 594
При каких х значения
функции у = х2
у = 25
2) не больше 25;
у 25
х [ 5; 5]
-5
5
х
15.
у№ 594
При каких х значения
функции у = х2
у = 16
3) не меньше 16;
у 16
х ( ; 4] [4; )
-4
4
х
16.
у№ 594
При каких х значения
функции у = х2
у = 36
4) меньше 36
у 36
х ( 6; 6)
-6
6
х
17.
a = 2, b = 0, c = 0y=
у
2
2x
0
х - 3 - 2 -1 0 1 2 3
у 18 8 2 0 2 8 18
1
х
18.
a = 0,5, b = 0, c = 0у
1 2
y= x
2
0
х - 3 - 2 -1 0 1 2 3
у 4,5 2 0,5 0 0,5 2 4,5
1
х
19.
y = ax2ya>1
y = ax2
0 < a <1
-1 0 1 2
x
20.
b = 0, c = 0y
у
2
= x–
0
х - 3 - 2 -1 0 1 2 3
у - 9 - 4 - 1 - 0 - 1 - 4 -9
1
х
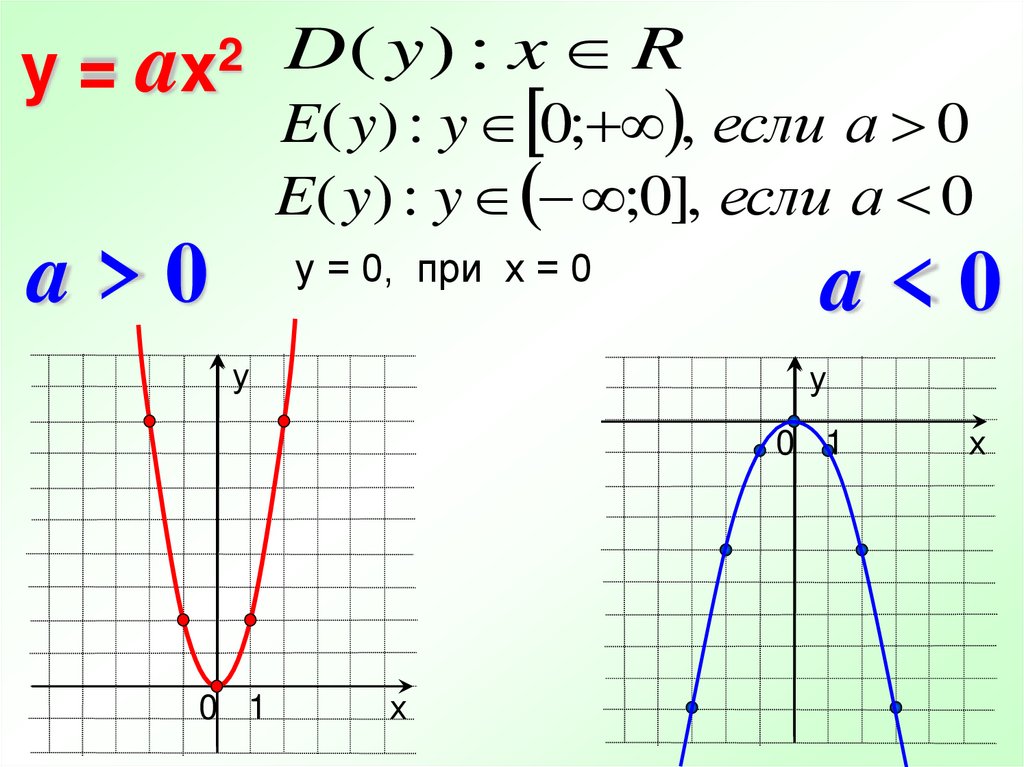
21.
y=a2
x
a>0
D( y ) : x R
E( y) : y 0; , если а 0
E( y) : y ;0], если а 0
у = 0, при х = 0
у
a<0
у
0 1
0 1
х
х
22.
y = ax2у(x) = y(-x), график функции симметричен
относительно оси ординат
у > 0, при х 0, при а > 0
a<0
у < 0, при х 0, при а < 0
a>0
у
у
0 1
0 1
х
х
23.
y x2
;0
y
0;
-1 0 1 2
x
24.
y = ax2a>0
у
Функция убывает
при х < 0
0
1
х
Функция возрастает
при х > 0
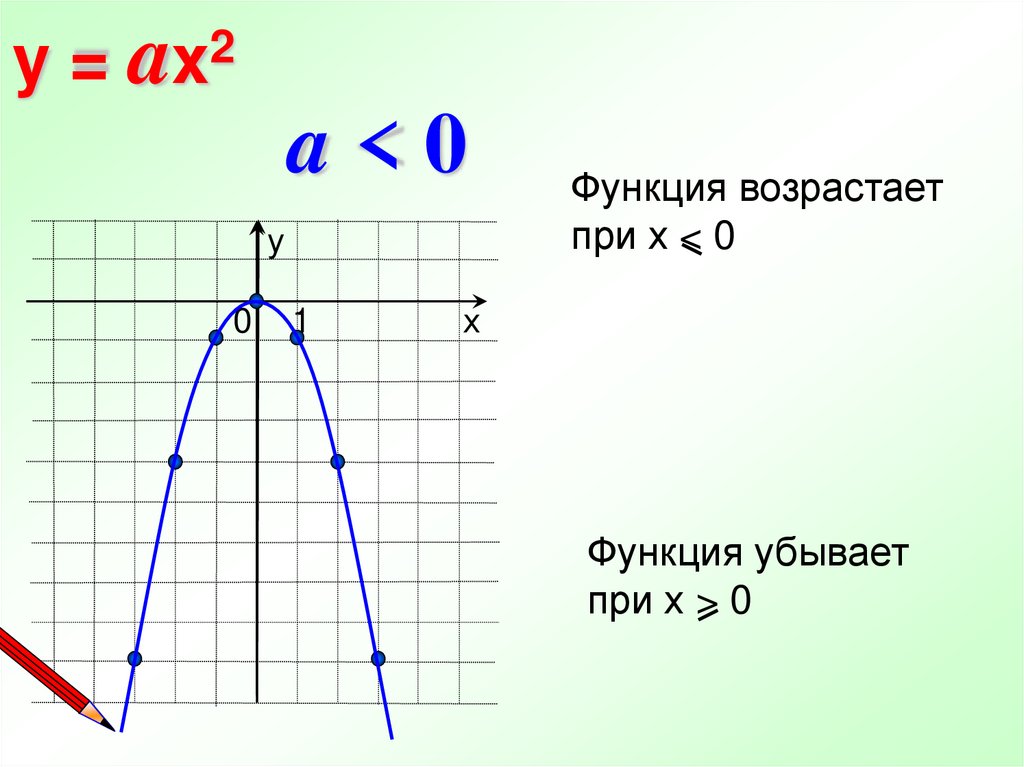
25.
y = ax2a<0
у
0
1
Функция возрастает
при х < 0
х
Функция убывает
при х > 0
26.
№ 599. С помощью графика функции у = – х2 решитьнеравенства.
2 х 8
2
у
-2
2
0
1
х
у = – 2х2
у=–8
х ( ; 2] [2; )
27.
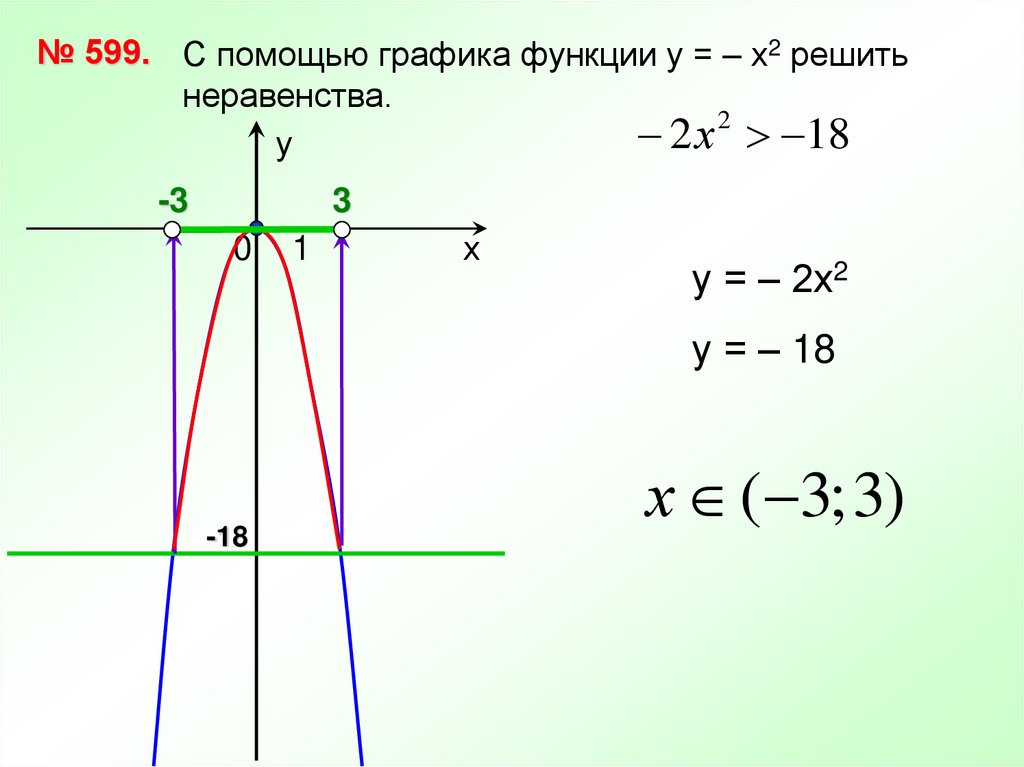
№ 599. С помощью графика функции у = – х2 решитьнеравенства.
2
2 х 18
у
-3
3
0
1
х
у = – 2х2
у = – 18
-18
х ( 3; 3)
28.
№ 599. С помощью графика функции у = – х2 решитьнеравенства.
2
2 х 32
у
-4
4
0
1
х
у = – 2х2
у = – 32
х [ 4; 4]
-32



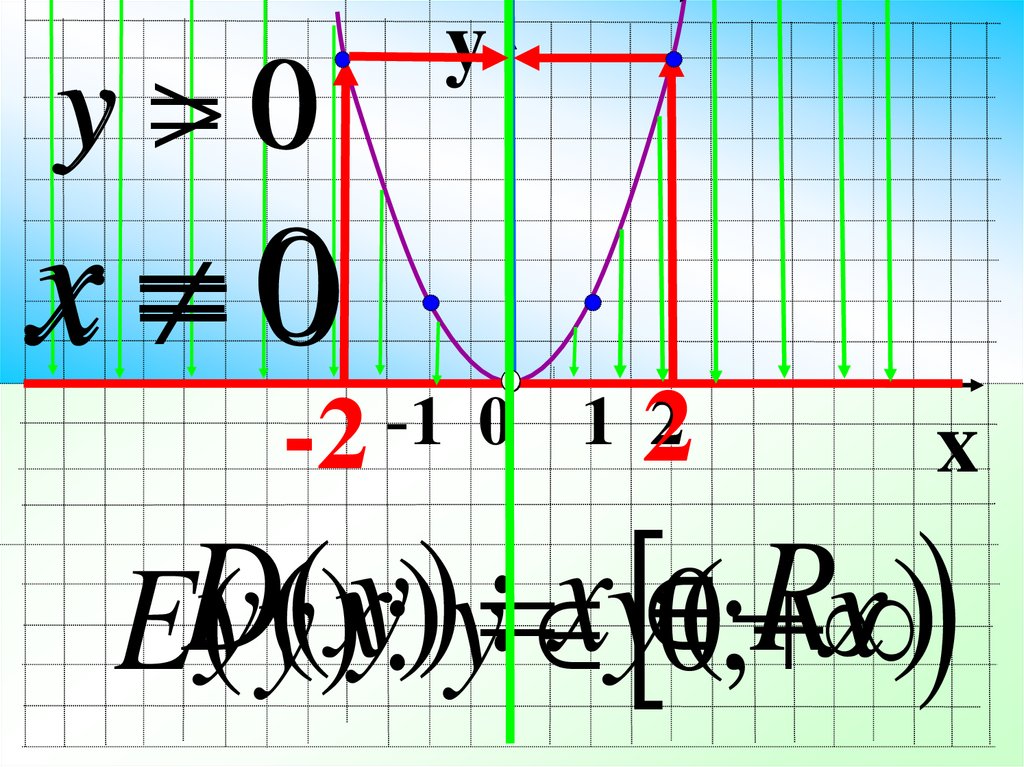




















 mathematics
mathematics








