Формулы приведения

1. ФОРМУЛЫ ПРИВЕДЕНИЯ

2.

ФОРМУЛЫ ПРИВЕДЕНИЯ
позволяют выразить значения
тригонометрических функций любого угла
через функции острого угла (угла I четверти)
Нужно и возможно ли запомнить все эти формулы?

3.

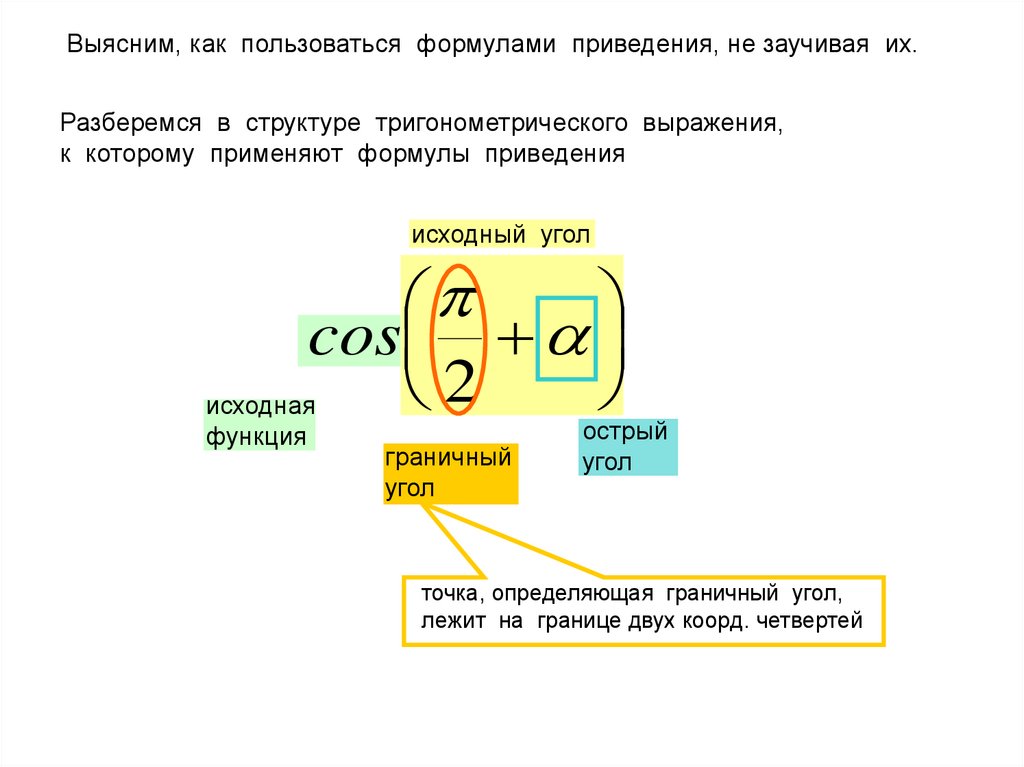
Выясним, как пользоваться формулами приведения, не заучивая их.
Разберемся в структуре тригонометрического выражения,
к которому применяют формулы приведения
исходный угол
cos
2
исходная
функция
граничный
угол
острый
угол
точка, определяющая граничный угол,
лежит на границе двух коорд. четвертей

4.

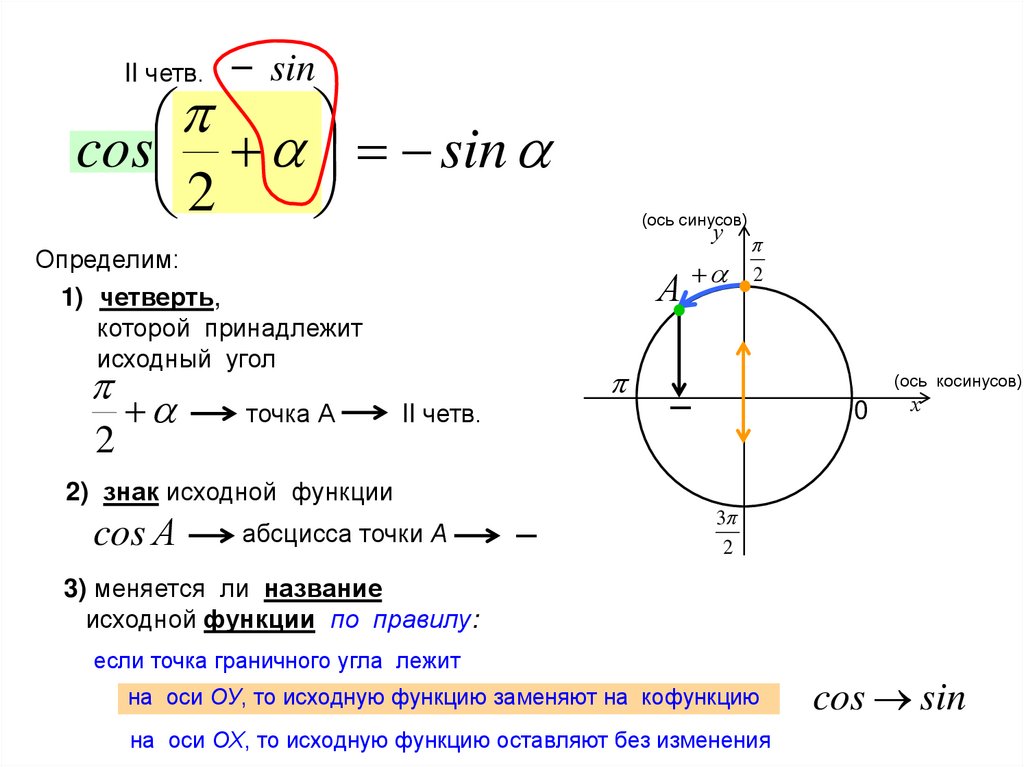
II четв.
¯ sin
cos sin
2
Определим:
1) четверть,
которой принадлежит
исходный угол
2
точка А
у
2
А
II четв.
абсцисса точки А
0
0
¯
2) знак исходной функции
cos А
(ось синусов)
¯
(ось косинусов)
х
3
2
3) меняется ли название
исходной функции по правилу:
если точка граничного угла лежит
на оси ОУ, то исходную функцию заменяют на кофункцию
на оси ОХ, то исходную функцию оставляют без изменения
cos sin

5.

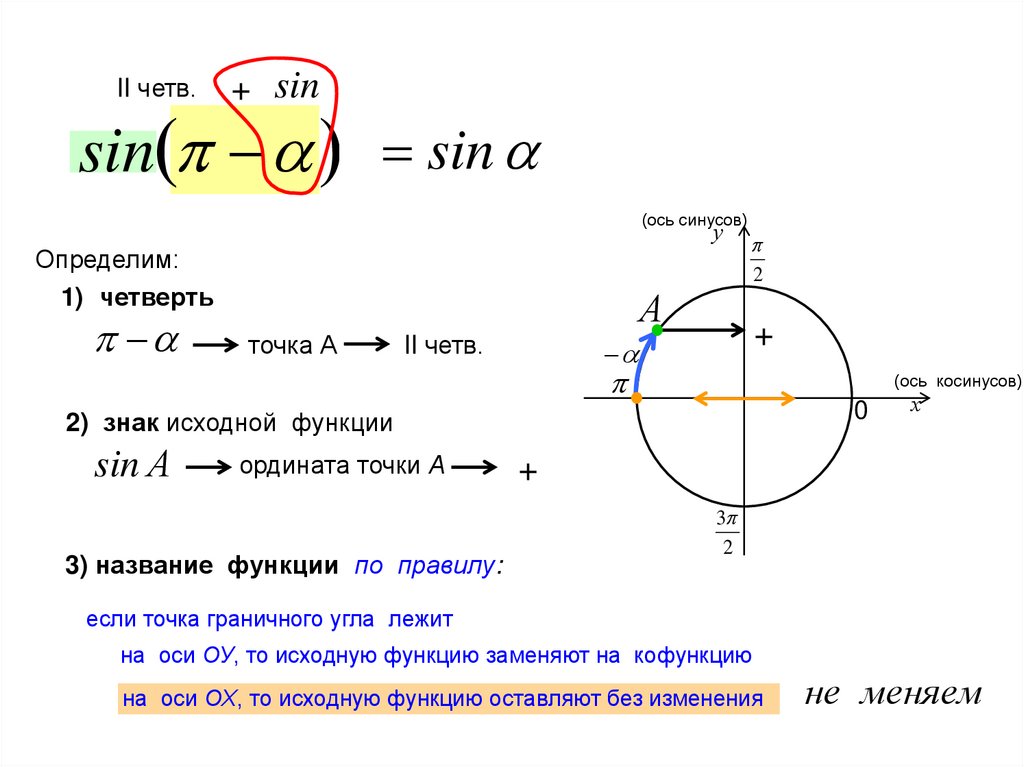
II четв.
+ sin
sin sin
(ось синусов)
у
Определим:
1) четверть
А
точка А
II четв.
2) знак исходной функции
sin А
2
ордината точки А
3) название функции по правилу:
+
0
0
(ось косинусов)
х
+
3
2
если точка граничного угла лежит
на оси ОУ, то исходную функцию заменяют на кофункцию
на оси ОХ, то исходную функцию оставляют без изменения
не меняем

6.

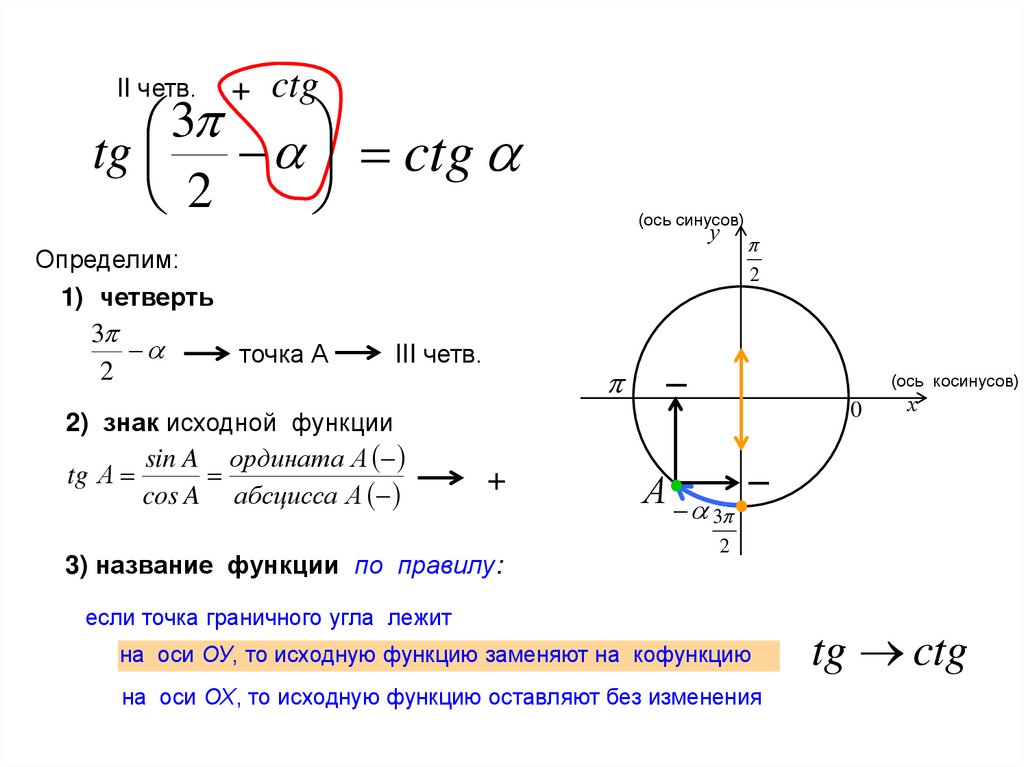
II четв.
+ ctg
3
tg ctg
2
(ось синусов)
у
2
Определим:
1) четверть
3
2
точка А
III четв.
2) знак исходной функции
sin A ордината А
tg А
cos A абсцисса А
+
3) название функции по правилу:
(ось косинусов)
¯
0
х
А• •¯
3
2
если точка граничного угла лежит
на оси ОУ, то исходную функцию заменяют на кофункцию
на оси ОХ, то исходную функцию оставляют без изменения
tg ctg

7.

Попытаемся применить формулы, определяя
1) четверть, 2) знак исходной функции, 3) меняем функцию?
без рисунка
III четв.
cos
3π¯
sin α cos
2
III четв.
+ cos
cos α cos
Найдите ошибки.
II четв.
tg
¯
tg α tg
π
cos α sin
2

8.

Домашнее задание