Similar presentations:
Формулы приведения. 10 класс
1. Формулы приведения
10 класс2.
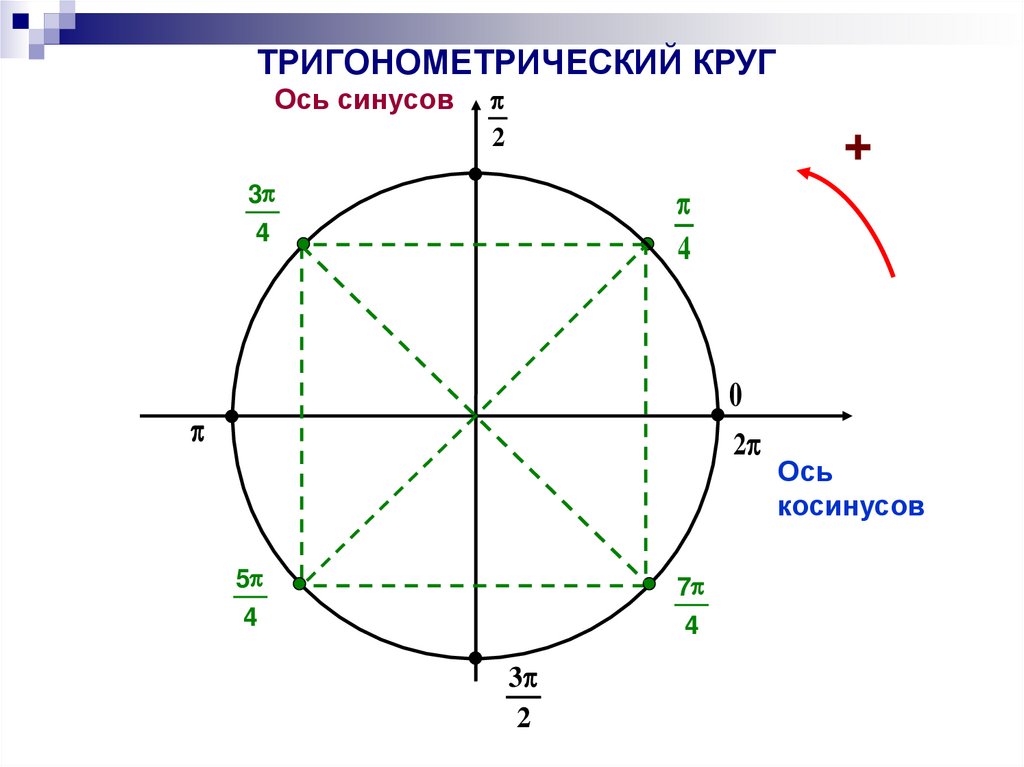
ТРИГОНОМЕТРИЧЕСКИЙ КРУГОсь синусов
2
+
3
4
4
0
2
5
4
7
4
3
2
Ось
косинусов
3.
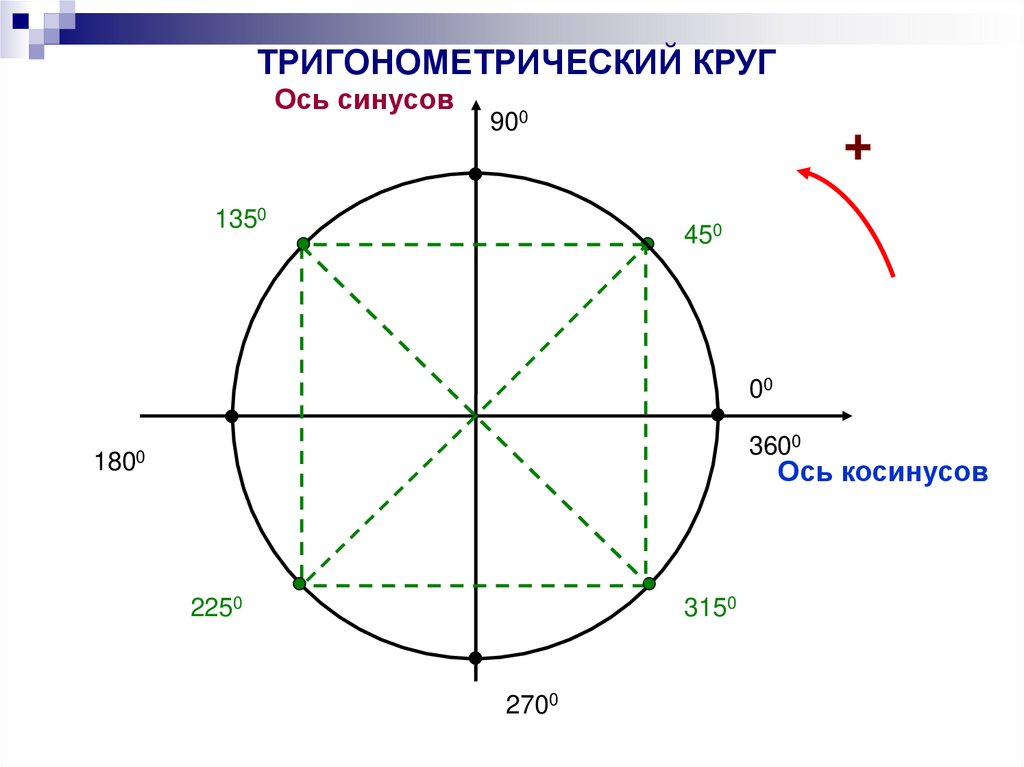
ТРИГОНОМЕТРИЧЕСКИЙ КРУГОсь синусов
900
1350
+
450
00
3600
1800
Ось косинусов
2250
3150
2700
4.
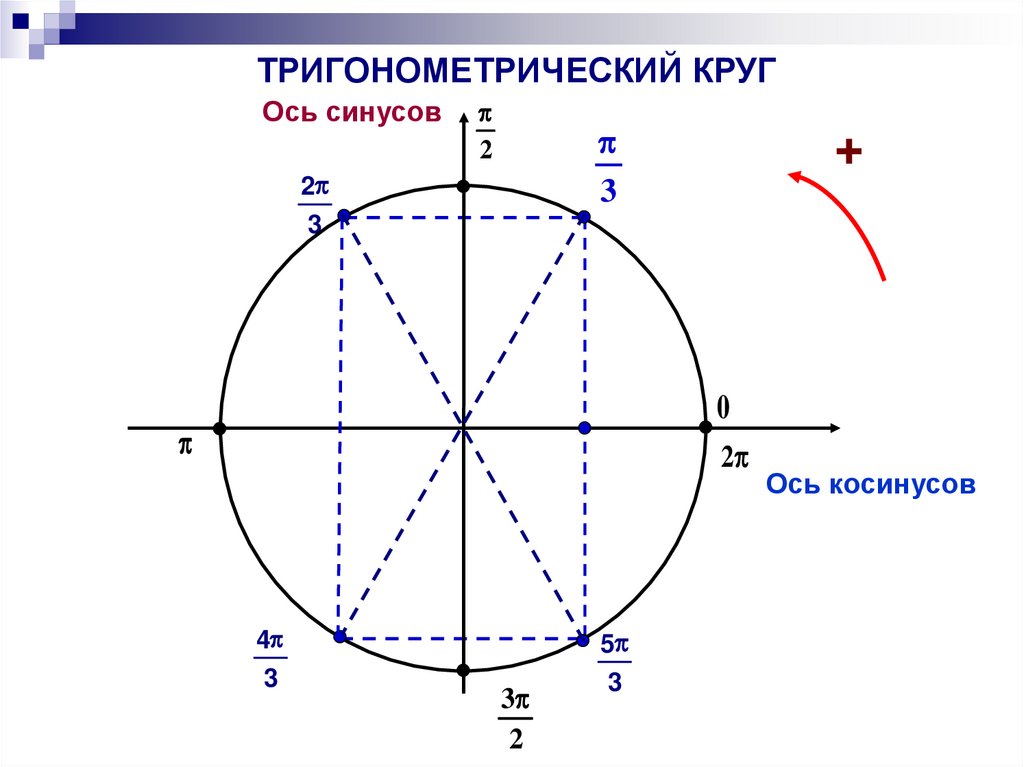
ТРИГОНОМЕТРИЧЕСКИЙ КРУГОсь синусов
2
3
2
3
+
0
2
4
3
3
2
5
3
Ось косинусов
5.
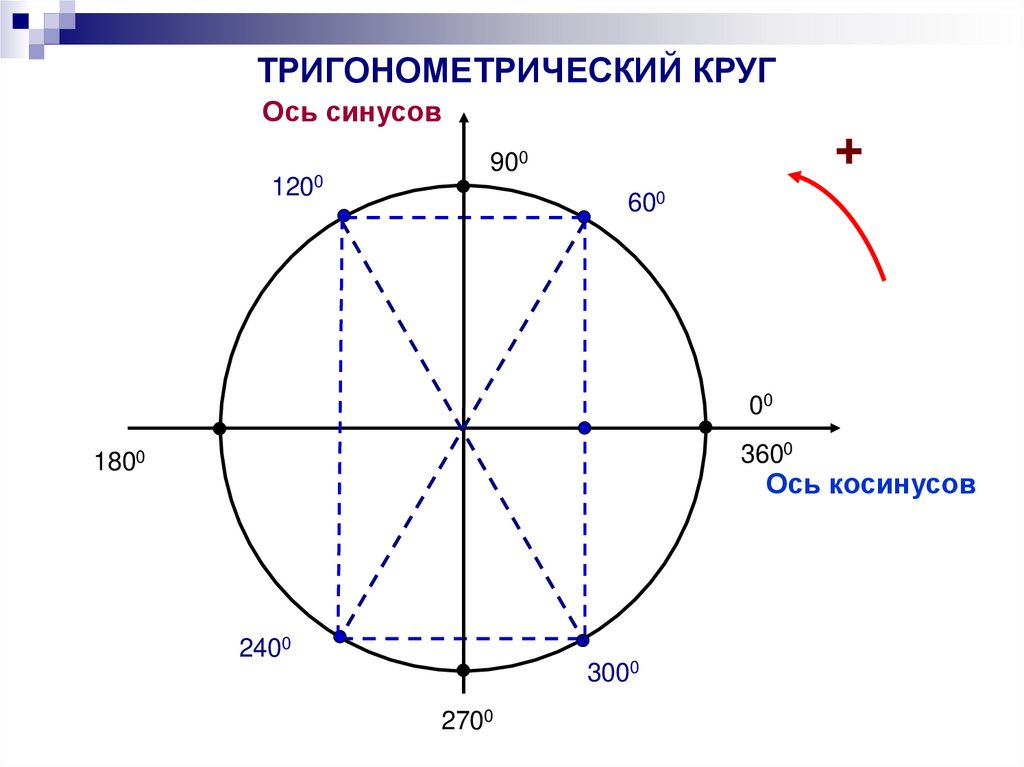
ТРИГОНОМЕТРИЧЕСКИЙ КРУГОсь синусов
1200
+
900
600
00
3600
1800
Ось косинусов
2400
3000
2700
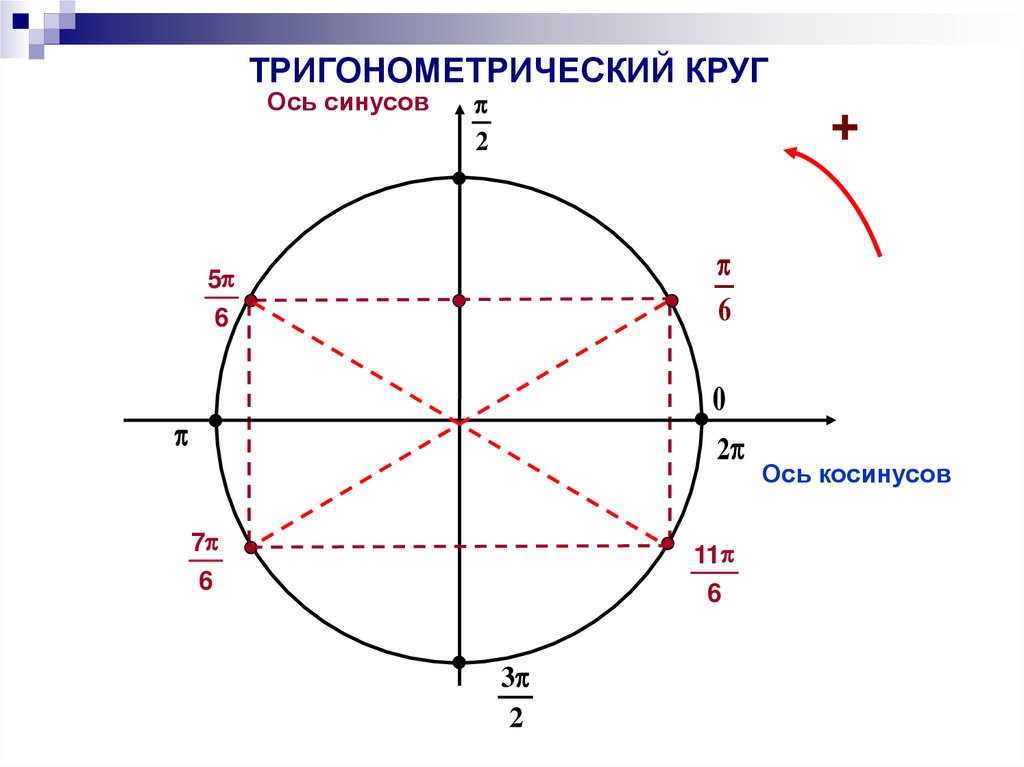
6.
ТРИГОНОМЕТРИЧЕСКИЙ КРУГОсь синусов
2
+
6
5
6
0
2
7
6
11
6
3
2
Ось косинусов
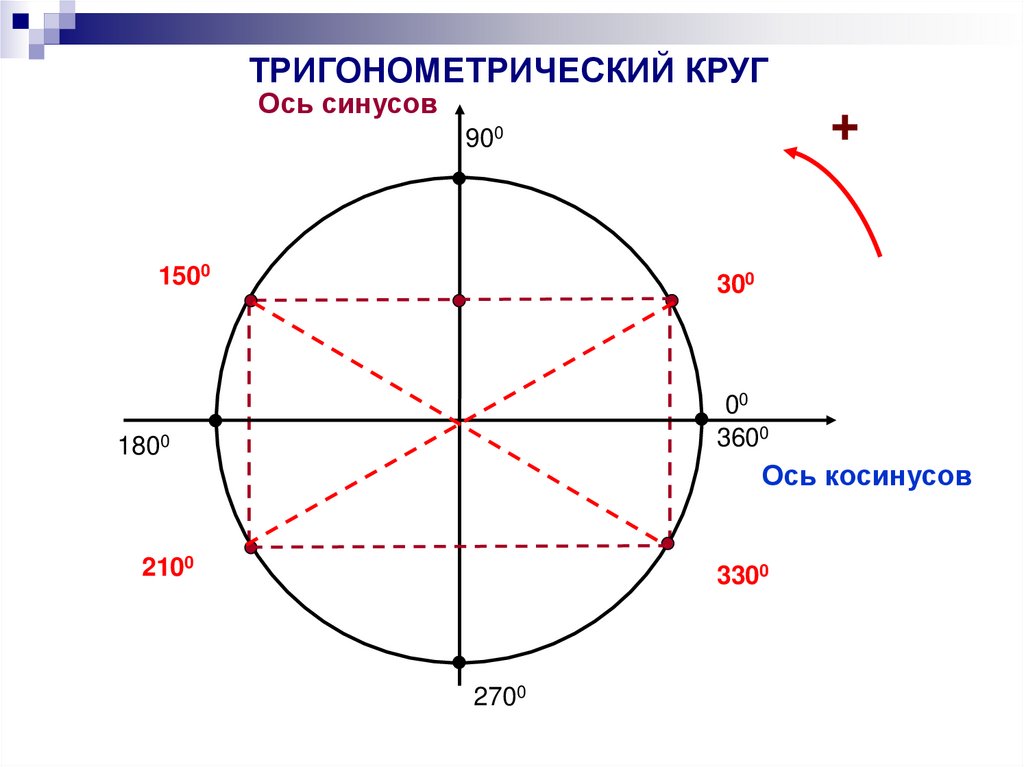
7.
ТРИГОНОМЕТРИЧЕСКИЙ КРУГОсь синусов
+
900
1500
300
00
3600
1800
Ось косинусов
2100
3300
2700
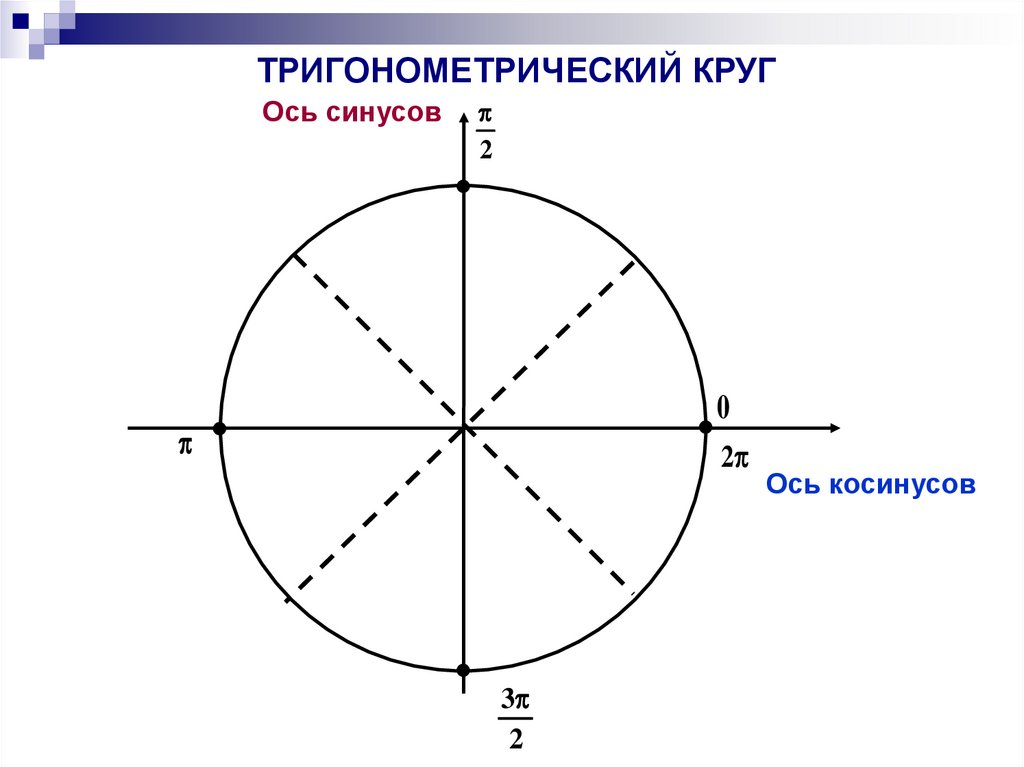
8.
ТРИГОНОМЕТРИЧЕСКИЙ КРУГОсь синусов
2
0
2
3
2
Ось косинусов
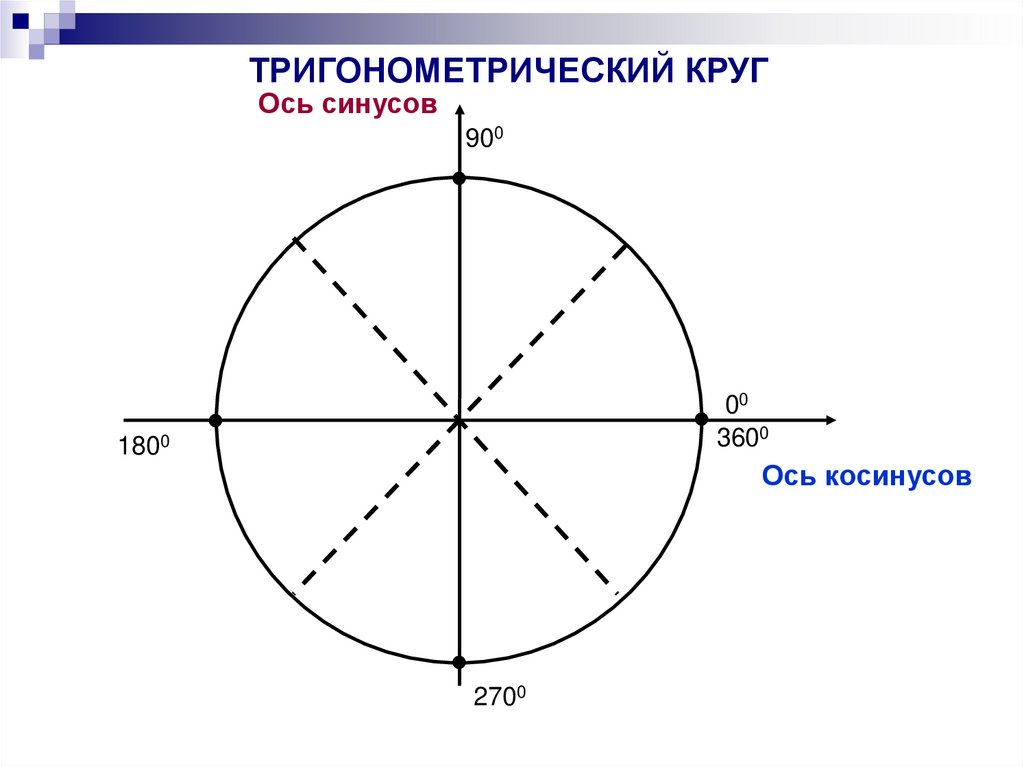
9.
ТРИГОНОМЕТРИЧЕСКИЙ КРУГОсь синусов
900
00
3600
1800
Ось косинусов
2700
10. Выводы
От границ четвертей можно выполнятьповорот
против
часовой стрелки ( знак + )
по часовой стрелке ( знак – )
при этом эти формулы называют
Формулами приведения
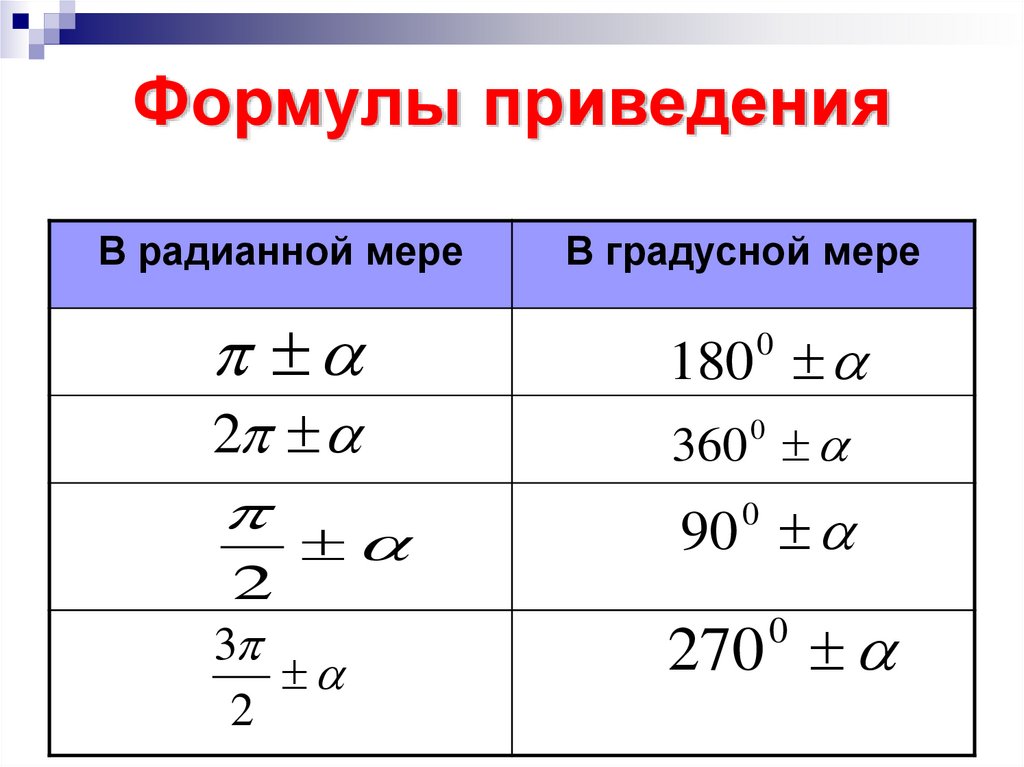
11. Формулы приведения
В радианной мере2
2
3
2
В градусной мере
180
0
360 0
90
0
270
0
12. Способ применения формул:
1. Если даны формулы2
360
180
0
0
название исходной функции
не меняется.
13. Способ применения формул:
2. Если даны формулы2
3
2
90
0
270
0
название исходной функции
заменяется на противоположную:
sin α cos α
tg α ctg α
14. Способ применения формул:
3. По формуле определить в какойчетверти находится угол и определить
знак исходной функции
4. Знак функции в правой части
совпадает со знаком исходной
функции
15. Рассмотрим примеры:
sin(2
II ч
) +
cos
Решение
1.Дана формула 2
, значит название функции
sin заменяем на противоположную cos.
2. 2
это угол II четверти, значит sin α > 0.
3. Знак + перед новой функции можно не ставить.
16.
IV чctg (360 )
0
ctg
Решение
1. Дана формула 3600 – α, значит
название функции ctg не меняем.
2. 3600 – α это угол IV четверти, значит
ctg α < 0.
3. Перед новой функцией ставим знак – .
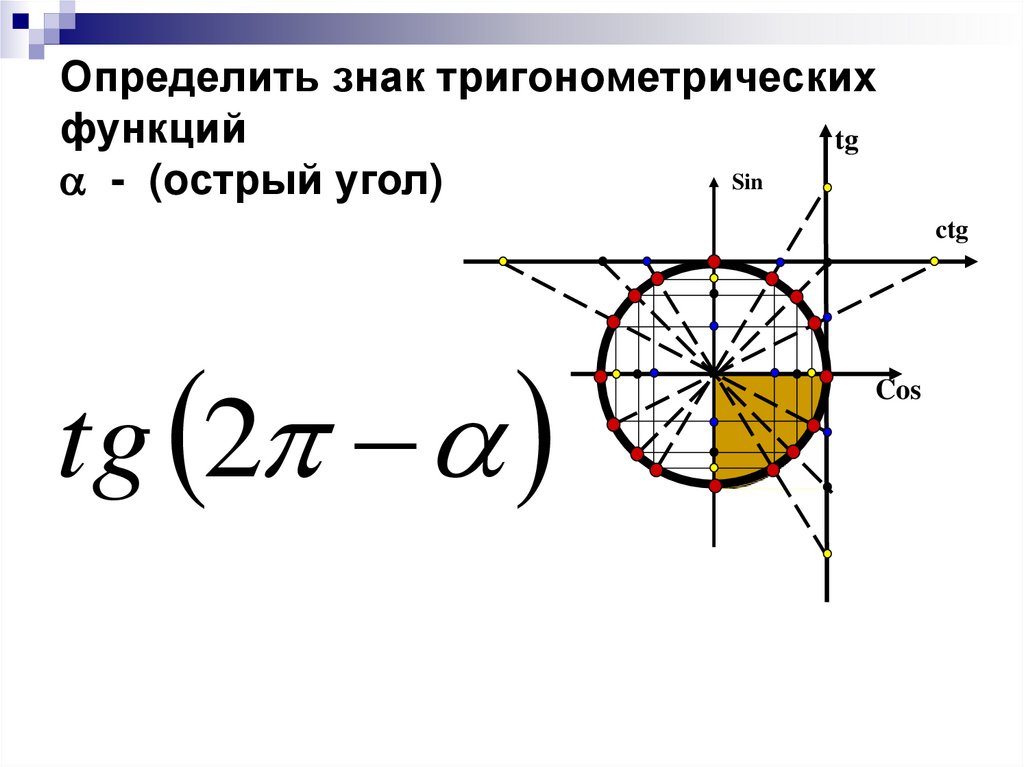
17. Определить знак тригонометрических функций, - (oстрый угол)
Определить знактригонометрических функций, tg Sin
(oстрый угол)
ctg
ctg ( )
Cos
18. Определить знак тригонометрических функций, - (oстрый угол)
Определить знакtg
тригонометрических функций,
Sin
- (oстрый угол)
ctg
ctg
2
Sin
2
Cos
19. Определить знак тригонометрических функций - (oстрый угол)
Определить знак тригонометрическихфункций
tg
Sin
- (oстрый угол)
ctg
tg 2
Cos
20. Определить знак тригонометрических функций, - (oстрый угол)
Определить знактригонометрических функций, tg Sin
(oстрый угол)
ctg
Sin
Cos
21. Выполните следующие задания:
1 заданиесos (П - )
tg ( 3 )
2
ctg(
2 )
sin(1800 + )
ответ
22.
Выполните следующие задания:2 задание
ответ
sin( )
cos( 270 )
0
tg (
2
)
ctg ( 360 )
0
23.
Выполните следующие задания:3 задание
2
sin (
2
ответ
)
ctg (2 )
2
Когда дана функция в квадрате, то четверть не
определяют!!!
Работает только «смена» функций, если дана
«рабочая» формула приведения!!
24.
25. Выполните тест
1.Поставьте вместо звёздочки такое число,при котором наименование функции меняться:
А) не будет
Б) будет
sin(
cos(
tg(
ctg(
*
*
*
*
- a)
+ a)
+ a)
- a)
sin( *
cos( *
tg( *
ctg( *
+ a)
- a)
+ a)
- a)
26. Выполните тест
2. Замените одно из слагаемых в аргументетригонометрической функции так, чтобы
функция поменяла название:
А) sin(π – t)
Б) cos(2π + t)
В) tg(3600 – t)
Г) ctg(7200 + t)
27. Выполните тест
3. Поставьте вместо звёздочки число так, чтобыполучившееся равенство стало верным:
А) sin(
Б) cos(
В) tg(
Г) sin(
Д) ctg(
*
*
*
*
*
+ t) = – cos t
- t) = sin t
+ t) = – ctg t
+ t) = – sin t
- t) = tg t
28. Выполните тест
4.Поставьте вместо звёздочки знак «+» или«-» так, чтобы получилось верное равенство:
А) sin(
2
- t) = * cos t
Б) cos( 2 ) = * cos
В) cos( 3 ) = * sin
2
Г) tg(2700 + t) = * ctg t
Д) ctg(3600 + t) = * сtg t
29. Выполните тест
5. Упростите:А)
Б)
В)
Г)
cos ( )
2
sin(3600 – t)
tg(2π + t)
ctg(3π - t)
30. Выполните задание
1.Вычислите с помощью формул приведения:в градусной мере
А) sin 2400 =
Б) tg 1200 =
В) cos 3000 =
Г) ctg 3150 =
Д) sin(- 5100) =



















 mathematics
mathematics








