Similar presentations:
Формулы приведения
1. На модели тригонометрического круга покажите углы и назовите четверть, в которой располагается данный угол
1940,1260,
3720,
2780.
третья
вторая
первая
четвертая
Назовите граничные углы в пределах от 0 до 2π.
Чему равен sin90º,cos90º, sin π, cos π , sin270º,cos270º.
Представьте углы 1940 ,1260, 3720 , 2780 в виде суммы
граничного и острого.
2. На модели тригонометрического круга покажите углы, назовите четверть и знаки тригонометрических функций этих углов
22
вторая
четвёртая
третья
3
2
третья
3.
Чему равен cos30˚, sin60˚, cos390˚, sin420˚,9
5
сos , cos
, cos
?
4
4
4
4. Формулы приведения
Цели урока:• доказать формулы приведения;
• рассмотреть примеры применения формул
приведения к вычислению тригонометрических
функций различных углов
5.
,,
,
,
,
,
,
.
Определение
Формулами приведения называют формулы,
позволяющие привести тригонометрические
функции аргументов
2
, ,
к аргументу
3
, 2 .
2
6. Известны!
соs (sin(
2
2
) sin
) cos
7.
Работа по группам:доказать формулу, используя формулы сложения
1) cos(
2) sin(
2
2
)
sin
)
cos
3) cos( )
3
4) sin(
)
2
5) sin( )
3
6) cos( )
2
cos
сos
sin
sin
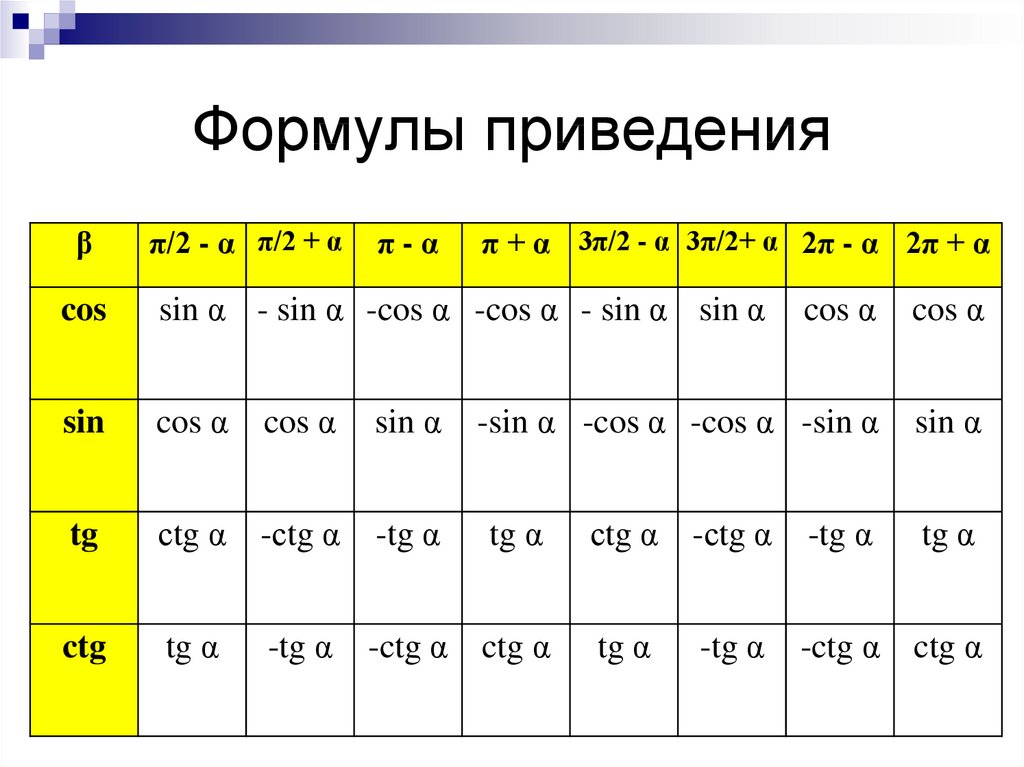
8. Формулы приведения
βπ/2 - α π/2 + α
π-α
π + α 3π/2 - α 3π/2+ α 2π - α 2π + α
cos
sin α - sin α -cos α -cos α - sin α sin α
cos α
cos α
sin
cos α -cos α sin α
-sin α -cos α cos α -sin α
sin α
9. Формулы приведения
βπ/2 - α π/2 + α
π-α
π + α 3π/2 - α 3π/2+ α 2π - α 2π + α
cos
sin α - sin α -cos α -cos α - sin α sin α
sin
cos α
cos α
sin α
tg
сtg α -сtg α
-tg α
ctg
tg α
-ctg α ctg α
-tg α
cos α
cos α
-sin α -cos α -cos α -sin α
sin α
tg α
сtg α -сtg α
-tg α
tg α
-ctg α ctg α
-tg α
tg α
10. Мнемоническое правило записи формулы приведения
1.2.
В правой части формулы ставится тот знак,
который имеет левая часть при условии 0
2
Если в левой части формулы угол равен
3
,
, то синус заменяется на косинус,
2
2
тангенс - на котангенс и наоборот.
Если угол равен ,2 , то замены не
происходит.
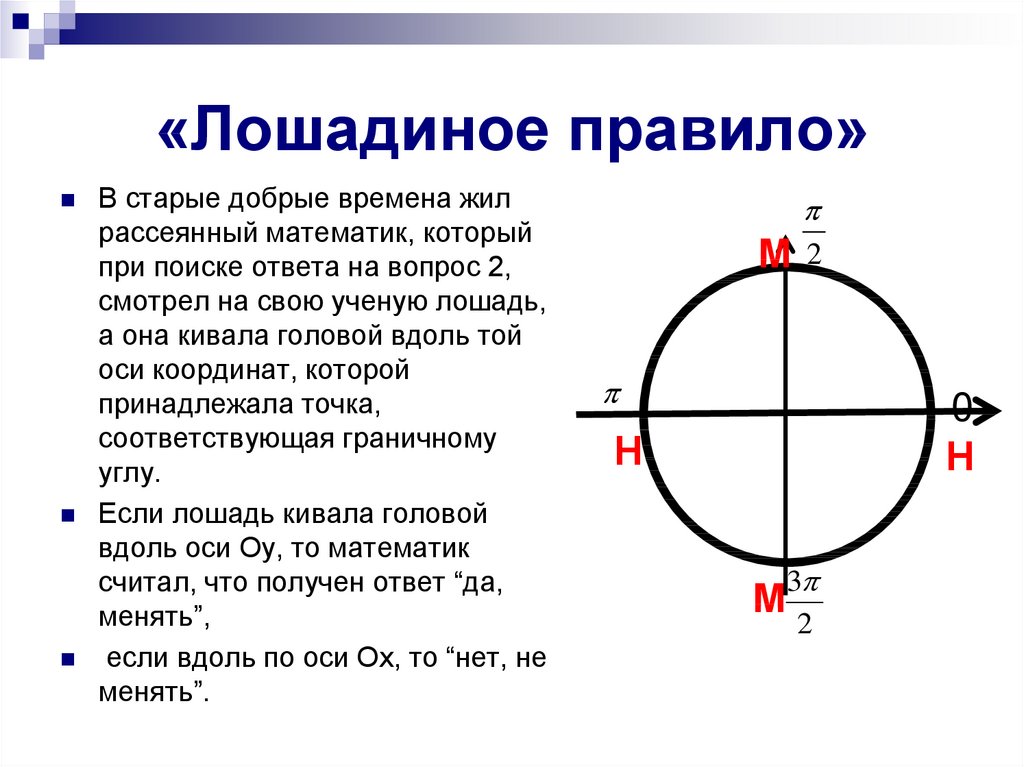
11. «Лошадиное правило»
В старые добрые времена жилрассеянный математик, который
при поиске ответа на вопрос 2,
смотрел на свою ученую лошадь,
а она кивала головой вдоль той
оси координат, которой
принадлежала точка,
соответствующая граничному
углу.
Если лошадь кивала головой
вдоль оси Оу, то математик
считал, что получен ответ “да,
менять”,
если вдоль по оси Ох, то “нет, не
менять”.
М
2
0
Н
Н
3
М
2
12.
Воспользовавшись мнемоническимправилом записать формулу приведения
3
1) sin(
)
2
2)tg ( )
3)ctg (
2
)
М
2
0
Н
Н
3
М
2
13.
Примеры на вычисление:1) cos 120
2) sin 135
5
3) cos
4
14.
Вычислите самостоятельно:1) cos 225
2) sin 315
3
3)tg
4
7
4) cos( )
3
15. Домашнее задание
Выучить мнемоническое правило дляформул приведения;
№ 154, 155 (всем),
158 (по желанию).
Презентация об Эйлере (по желанию
после каникул).













 mathematics
mathematics








