Similar presentations:
Тригонометрия. Формулы приведения
1. «ФОРМУЛЫ ПРИВЕДЕНИЯ»
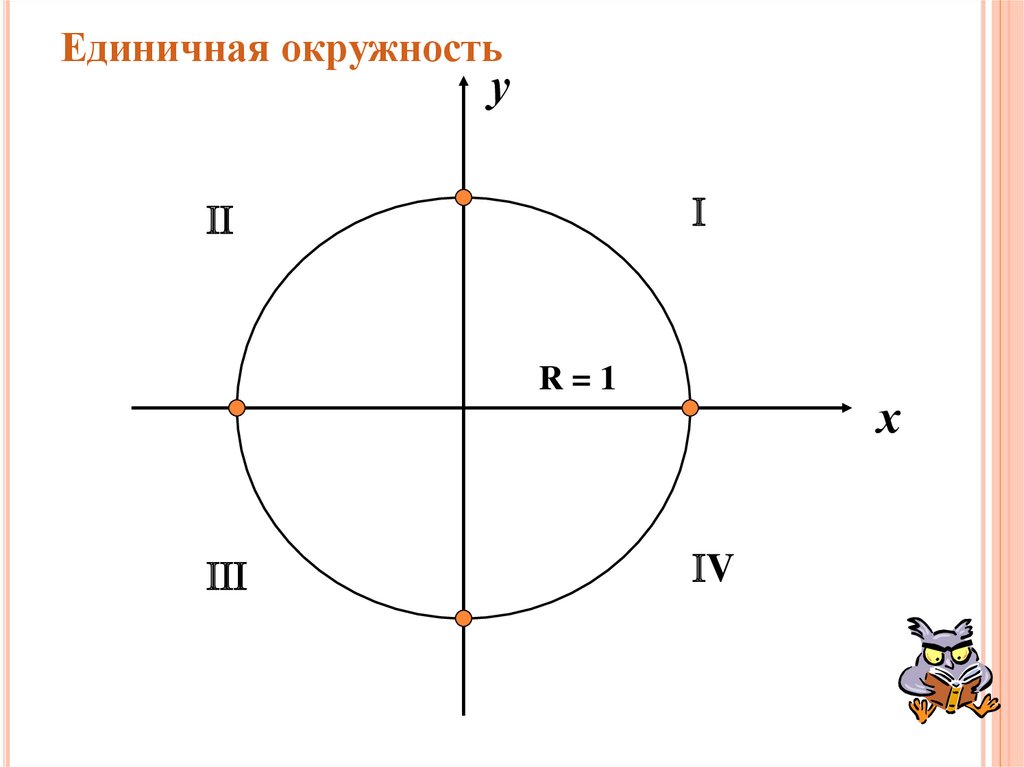
2. Единичная окружность
уR=1
х
V
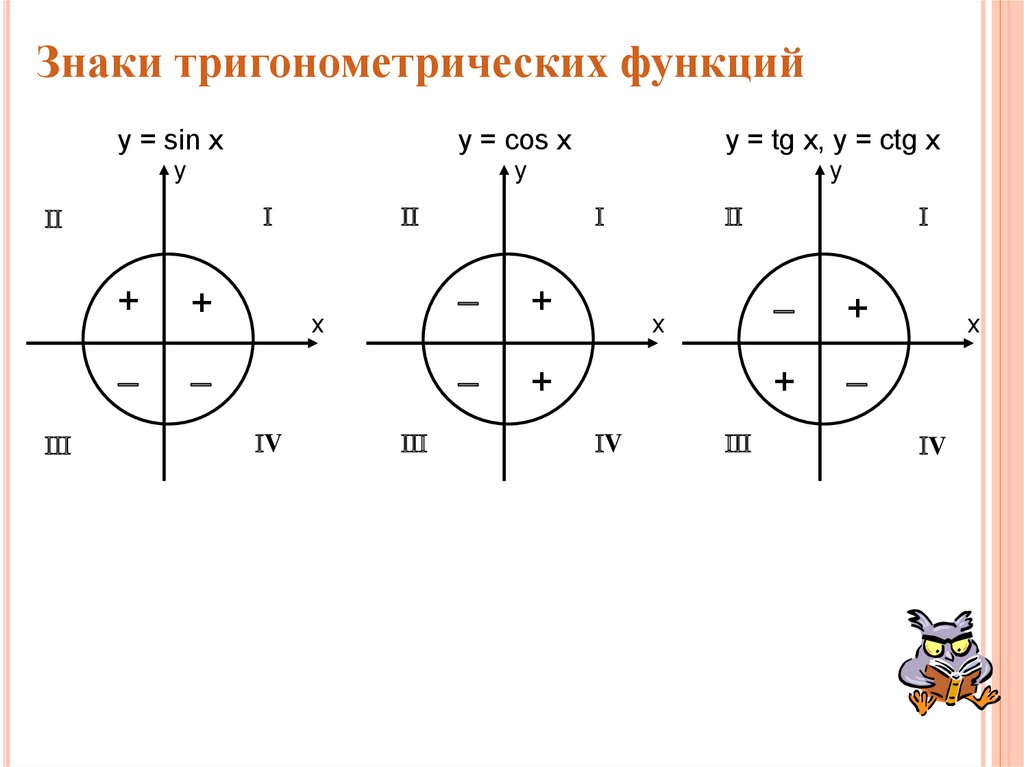
3. Знаки тригонометрических функций
y = sin xy = cos x
y = tg x, y = ctg x
y
y
y
+
+
x
V
+
+
x
V
+
+
x
V
4. Определите четверть:
ОПРЕДЕЛИТЕ ЧЕТВЕРТЬ:96
273
120
2
2
3
2
3
2
5.
1cos 60° =
2
1
sin =
2
6
tg 45° = 1
3
ctg 3 = 3
cos 135° = ?
6. ФОРМУЛЫ ПРИВЕДЕНИЯ
- это формулы, позволяющие выражатьзначения тригонометрических функций
любого угла через функции угла первой
четверти, т.е. < 90°.
90
0
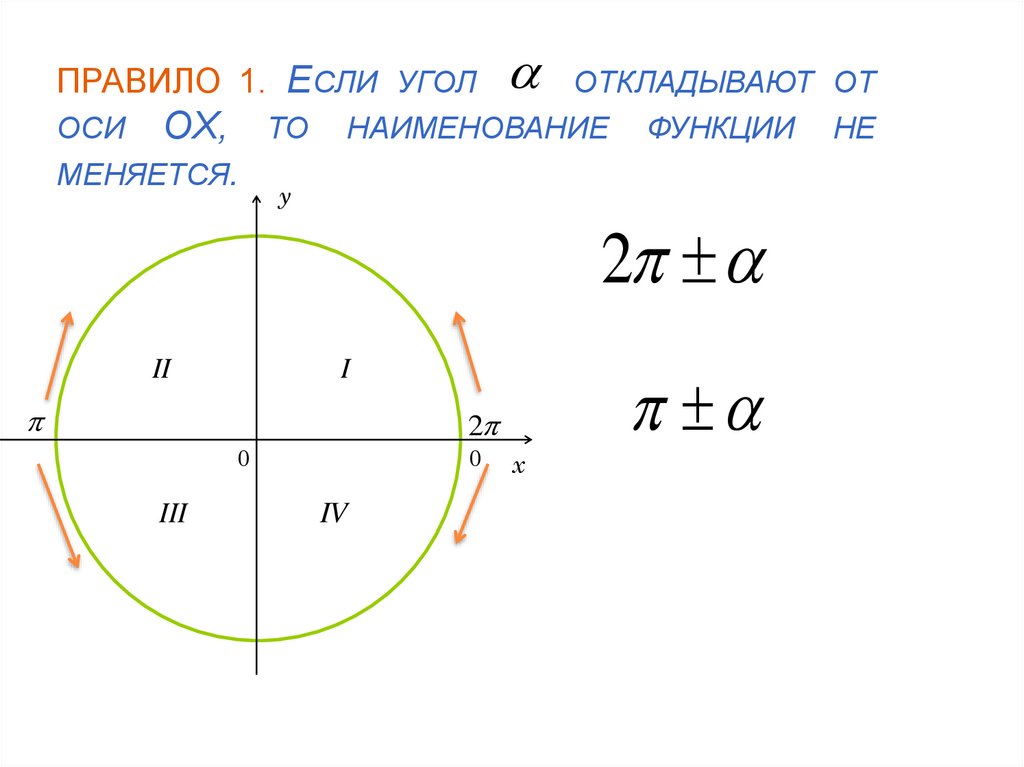
7. ПРАВИЛО 1. Если угол откладывают от оси ОX, то наименование функции не меняется.
ПРАВИЛО 1. ЕСЛИ УГОЛОСИ ОX, ТО
МЕНЯЕТСЯ.
НАИМЕНОВАНИЕ
y
II
ФУНКЦИИ
2
I
2
0
III
ОТКЛАДЫВАЮТ ОТ
0
IV
x
НЕ
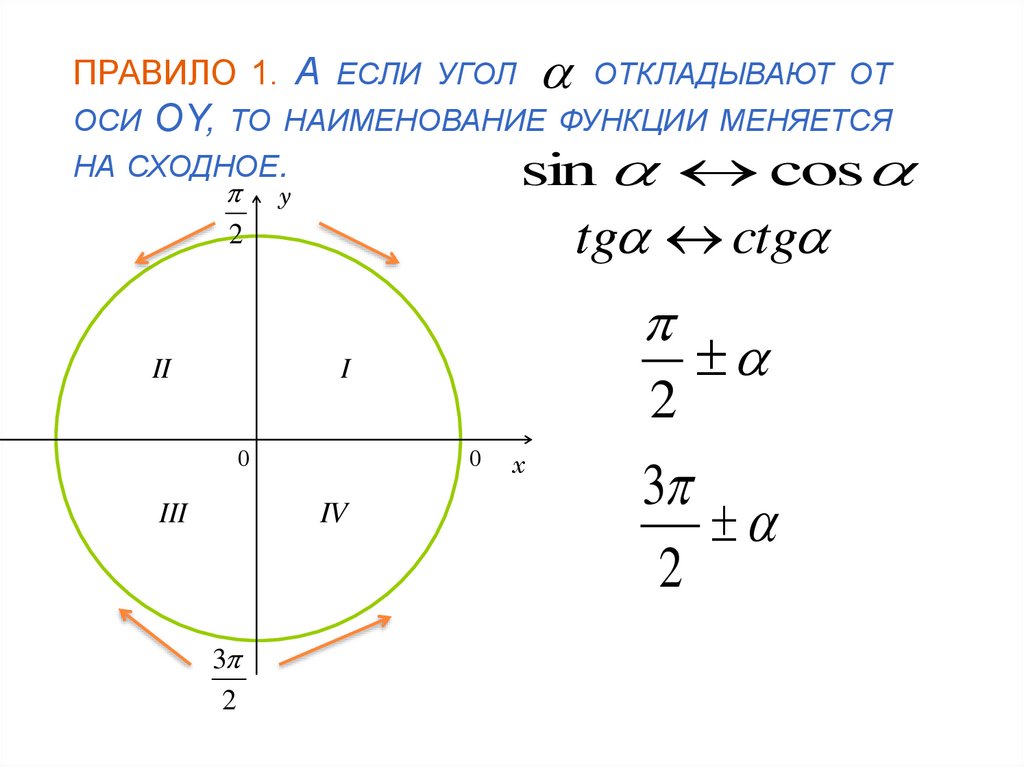
8. ПРАВИЛО 1. А если угол откладывают от оси ОY, то наименование функции меняется на сходное.
ПРАВИЛО 1. А ЕСЛИ УГОЛОСИ
ОY,
ОТКЛАДЫВАЮТ ОТ
ТО НАИМЕНОВАНИЕ ФУНКЦИИ МЕНЯЕТСЯ
sin cos
НА СХОДНОЕ.
y
tg ctg
2
II
I
0
0
IV
III
3
2
2
x
3
2
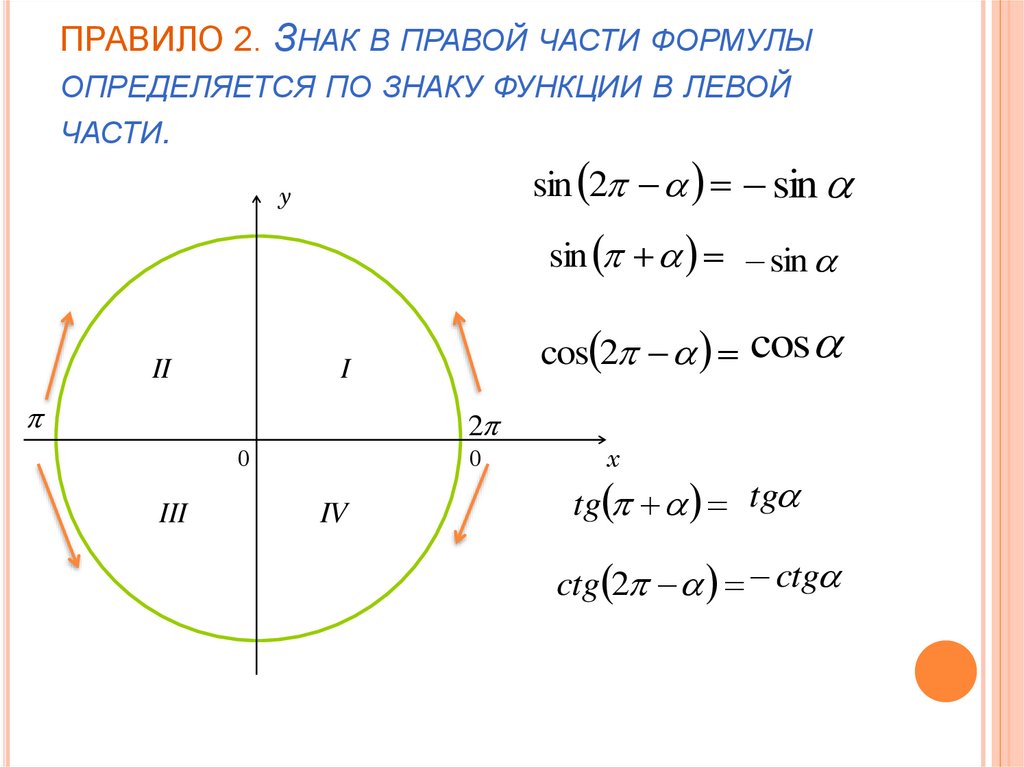
9. ПРАВИЛО 2. Знак в правой части формулы определяется по знаку функции в левой части.
ПРАВИЛО 2. ЗНАК В ПРАВОЙ ЧАСТИ ФОРМУЛЫОПРЕДЕЛЯЕТСЯ ПО ЗНАКУ ФУНКЦИИ В ЛЕВОЙ
ЧАСТИ.
sin 2 sin
y
sin sin
II
cos 2
I
2
0
III
0
IV
cos
x
tg tg
ctg 2 ctg
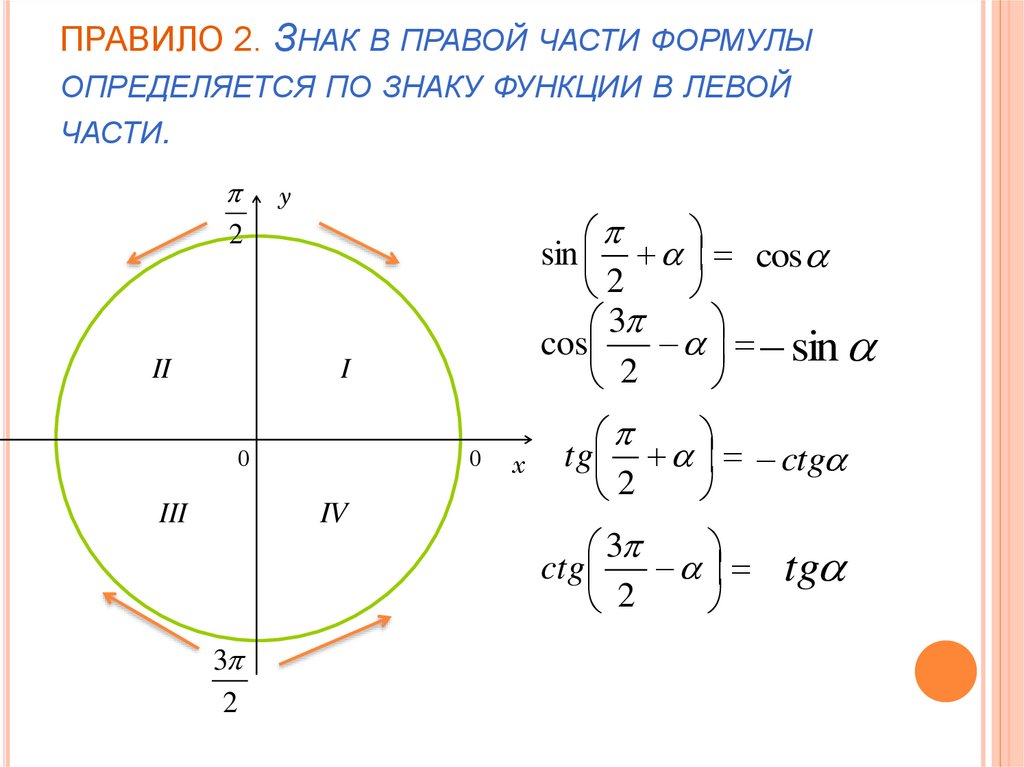
10. ПРАВИЛО 2. Знак в правой части формулы определяется по знаку функции в левой части.
ПРАВИЛО 2. ЗНАК В ПРАВОЙ ЧАСТИ ФОРМУЛЫОПРЕДЕЛЯЕТСЯ ПО ЗНАКУ ФУНКЦИИ В ЛЕВОЙ
ЧАСТИ.
2
II
y
sin cos
2
3
cos
sin
2
I
0
0
IV
III
3
2
x
tg ctg
2
3
ctg
2
tg
11. Запишите формулы приведения
ЗАПИШИТЕ ФОРМУЛЫ ПРИВЕДЕНИЯsin 90 0
tg 270
cos
ctg
cos 180 0 cos
0
sin 270 0 cos
sin
cos 90 0 sin
sin 360 0
12. Алгоритм применения формул приведения
1) Определить, какой координатной четвертипринадлежит угол;
2) Найти знак данной функции в этой четверти;
3) Определить, меняется данная функция на
«кофункцию» или нет:
sinα cosα
tgα ctgα
13. Задание 1.Выразите тригонометрические функции через угол меньше 45°.
ЗАДАНИЕ 1.ВЫРАЗИТЕ ТРИГОНОМЕТРИЧЕСКИЕФУНКЦИИ ЧЕРЕЗ УГОЛ МЕНЬШЕ 45°.
cos123
cos 90
33 sin 33
tg174
tg 180 6 tg6
sin 168 sin 180 12 sin 12
tg 263 tg 270 7 ctg 7
ctg 380 ctg 360 20 ctg 20
cos 969 cos 270 31 sin 31
14. ЗАДАНИЕ 2. Упростить выражение
3 cos 3 cos 360 cos 90 sin 1803 cos 3 cos sin sin
2sinα
15. ЗАДАНИЕ 3. Найти значение выражения:
IIcos (90° + 45°)
- sin 45°
2
cos 135° =
=
=
2
cos(180° - 45°)
- cos 45 °
4
sin
3
III
π
3π π
sin
= sin
3
3 3
3
- sin 2
3
16. Задание 4 . Упростить выражение
ЗАДАНИЕ 4 . Упростить выражениеsin 150° · tg225° =
sin 180 30 tg(180 45 )
= sin30 tg45
1
1
= 0,5
= 1
2
2
17. Задание 5. Упростить выражение
ЗАДАНИЕ 5. Упростить выражениеsin 150° · tg225° =
sin 180 30 tg(180 45 ) sin 90 60 tg(270 - 45 )
1
1
sin30
tg45
1
=
= cos60 ctg45 1
2
2
1
=
= 0,5
2
1
=
= 0,5
2


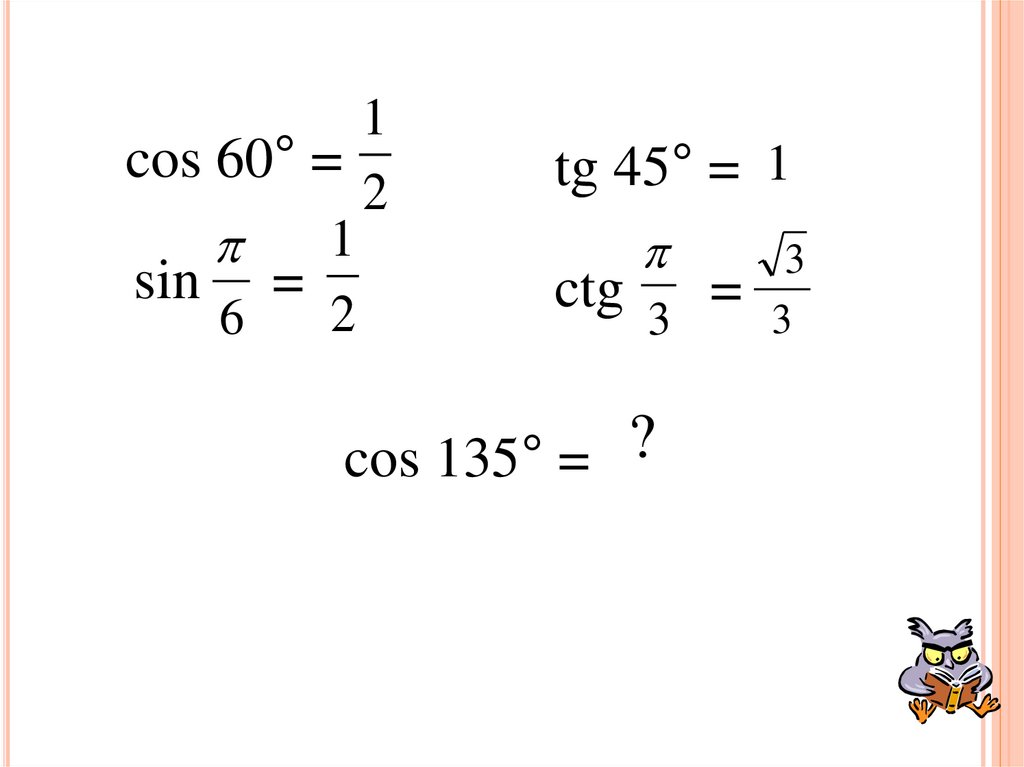









 mathematics
mathematics








