Similar presentations:
Формулы приведения
1. ФОРМУЛЫ ПРИВЕДЕНИЯ
2. ФОРМУЛЫ ПРИВЕДЕНИЯ
Позволяют вычислить значениятригонометрических функций угла любой четверти
через угол I четверти
3. Закончите формулы:
ЗАКОНЧИТЕ ФОРМУЛЫ:sin 50 cos 50
2
sin
cos
2
tg
cos cos sin sin
sin cos cos sin
1
4. Расставьте знаки:
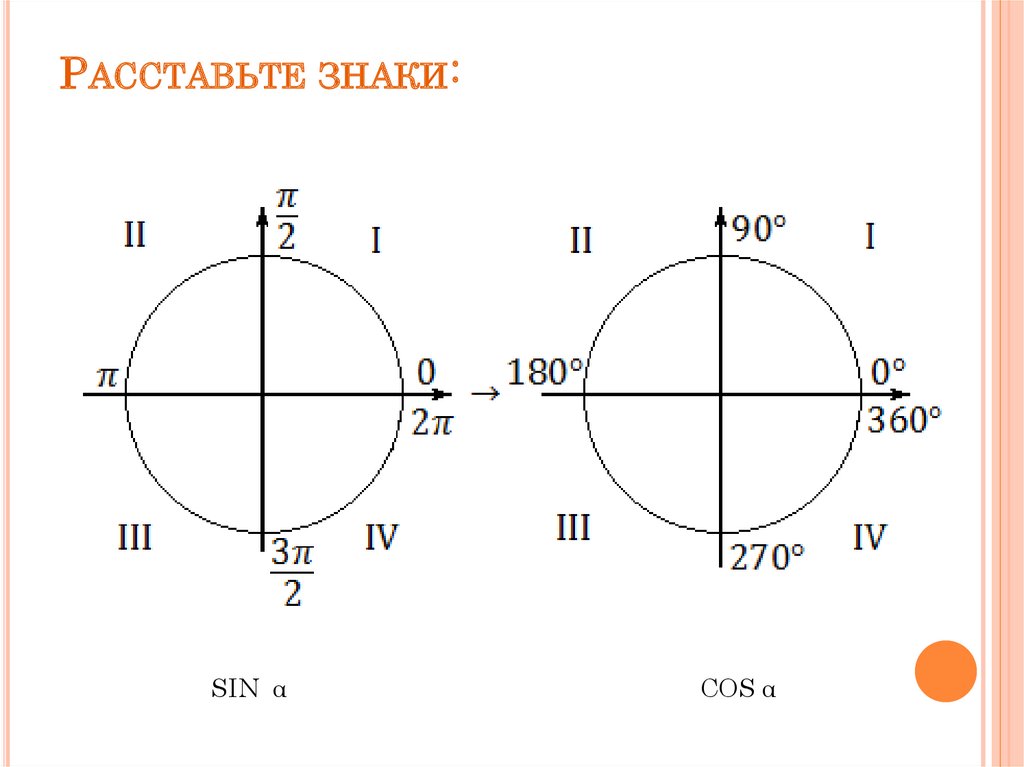
РАССТАВЬТЕ ЗНАКИ:SIN α
COS α
5. Определите четверть:
ОПРЕДЕЛИТЕ ЧЕТВЕРТЬ:96
273
120
2
2
3
2
3
2
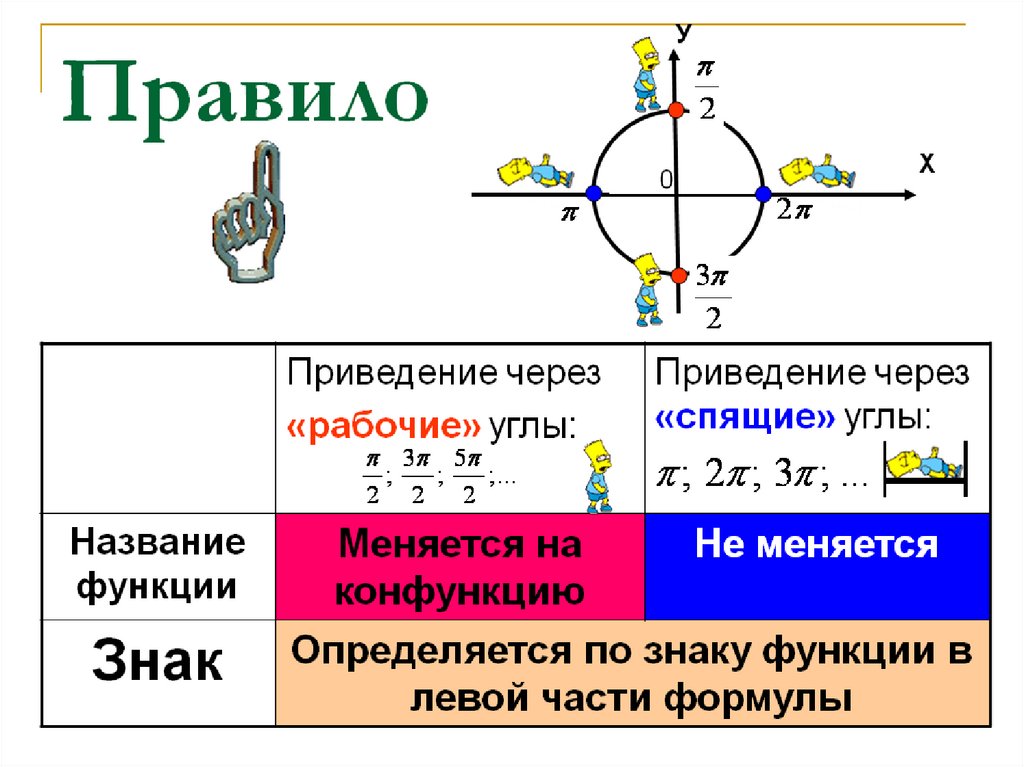
6. ПРАВИЛО 1. Если угол откладывают от оси ОX, то наименование функции не меняется.
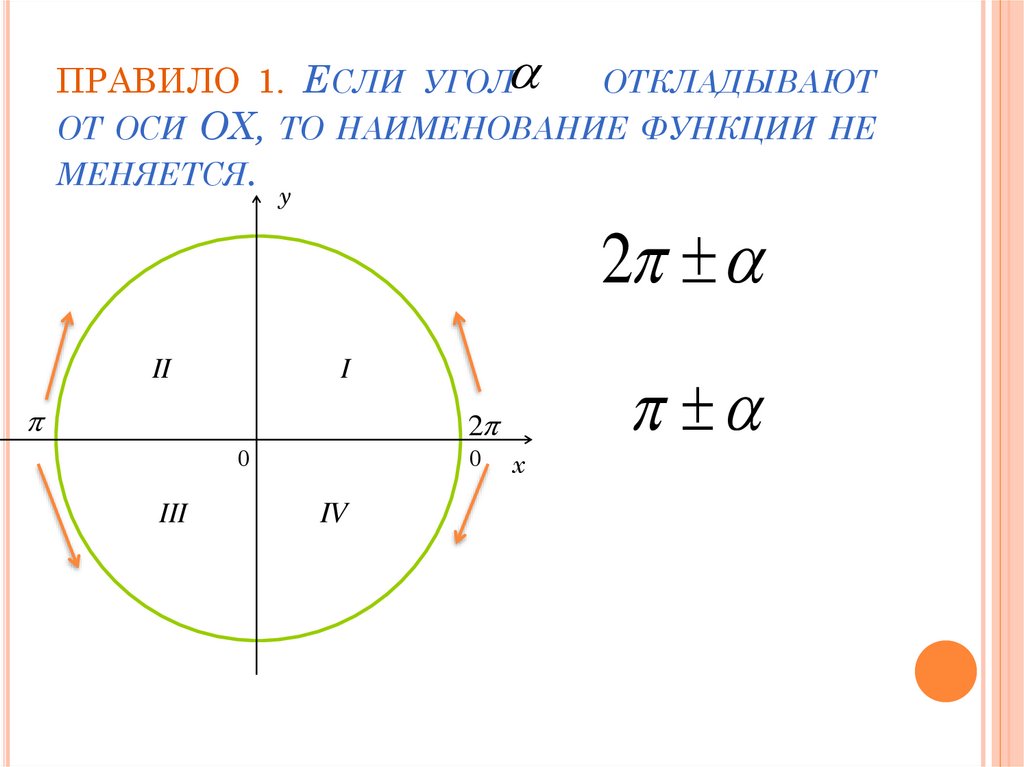
ПРАВИЛО 1. ЕСЛИ УГОЛОТКЛАДЫВАЮТ
ОТ ОСИ ОX, ТО НАИМЕНОВАНИЕ ФУНКЦИИ НЕ
МЕНЯЕТСЯ.
y
II
2
I
2
0
III
0
IV
x
7. ПРАВИЛО 1. А если угол откладывают от оси ОY, то наименование функции меняется на сходное.
ПРАВИЛО 1. А ЕСЛИ УГОЛОТ ОСИ
ОY,
ОТКЛАДЫВАЮТ
ТО НАИМЕНОВАНИЕ ФУНКЦИИ
cos
tg ctg
МЕНЯЕТСЯ НА СХОДНОЕ
.
sin
y
2
II
I
0
0
IV
III
3
2
2
x
3
2
8. ПРАВИЛО 2. Знак в правой части формулы определяется по знаку функции в левой части.
ПРАВИЛО 2. ЗНАК В ПРАВОЙ ЧАСТИФОРМУЛЫ ОПРЕДЕЛЯЕТСЯ ПО ЗНАКУ
ФУНКЦИИ В ЛЕВОЙ ЧАСТИ.
sin 2 sin
y
sin sin
II
cos 2
I
2
0
III
0
IV
cos
x
tg tg
ctg 2 ctg
9. ПРАВИЛО 2. Знак в правой части формулы определяется по знаку функции в левой части.
ПРАВИЛО 2. ЗНАК В ПРАВОЙ ЧАСТИФОРМУЛЫ ОПРЕДЕЛЯЕТСЯ ПО ЗНАКУ
ФУНКЦИИ В ЛЕВОЙ ЧАСТИ.
2
II
y
sin cos
2
3
cos
sin
2
I
0
0
IV
III
3
2
x
tg ctg
2
3
ctg
2
tg
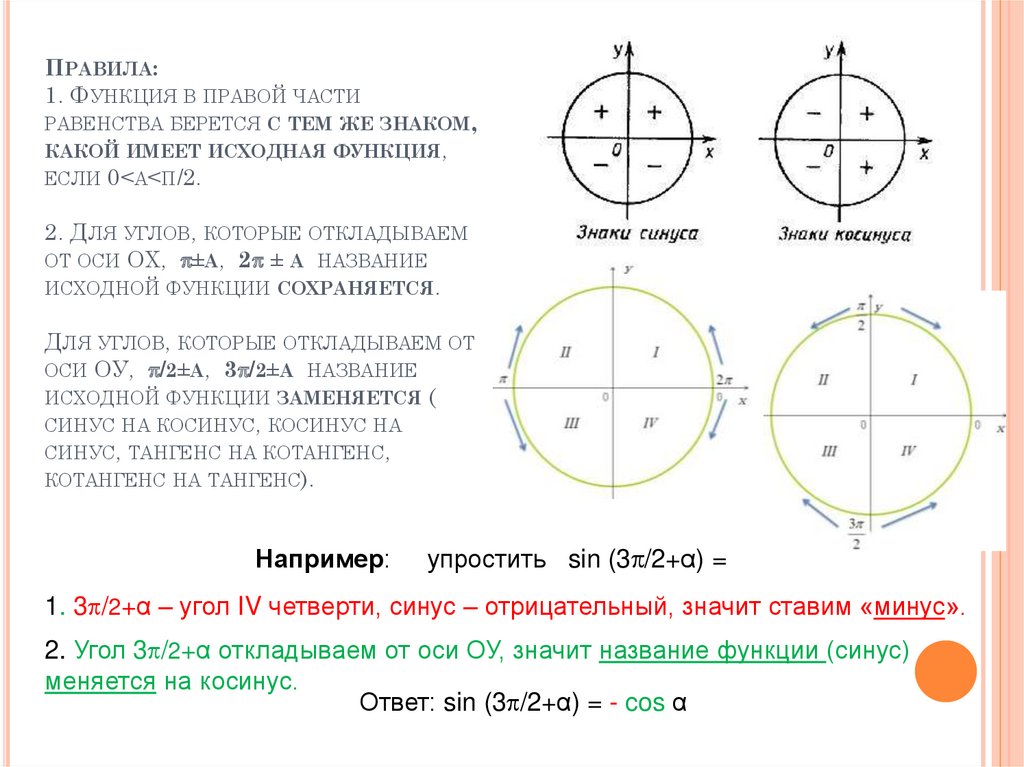
10. Правила: 1. Функция в правой части равенства берется с тем же знаком, какой имеет исходная функция, если 0<α<π/2. 2. Для
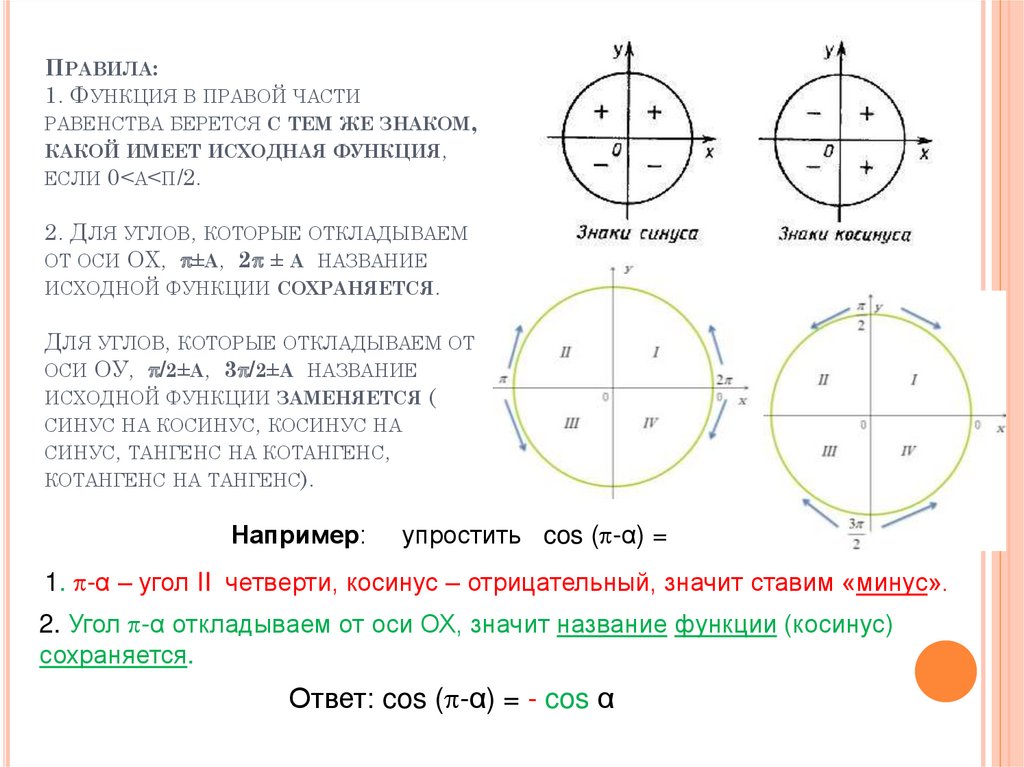
ПРАВИЛА:1. ФУНКЦИЯ В ПРАВОЙ ЧАСТИ
РАВЕНСТВА БЕРЕТСЯ С ТЕМ ЖЕ ЗНАКОМ,
КАКОЙ ИМЕЕТ ИСХОДНАЯ ФУНКЦИЯ,
ЕСЛИ 0<Α<Π/2.
2. ДЛЯ УГЛОВ, КОТОРЫЕ ОТКЛАДЫВАЕМ
ОТ ОСИ ОХ, ±Α, 2 ± Α НАЗВАНИЕ
ИСХОДНОЙ ФУНКЦИИ СОХРАНЯЕТСЯ.
ДЛЯ УГЛОВ, КОТОРЫЕ ОТКЛАДЫВАЕМ ОТ
ОСИ ОУ, /2±Α, 3 /2±Α НАЗВАНИЕ
ИСХОДНОЙ ФУНКЦИИ ЗАМЕНЯЕТСЯ (
СИНУС НА КОСИНУС, КОСИНУС НА
СИНУС, ТАНГЕНС НА КОТАНГЕНС,
КОТАНГЕНС НА ТАНГЕНС).
Например:
упростить cos ( -α) =
1. -α – угол II четверти, косинус – отрицательный, значит ставим «минус».
2. Угол -α откладываем от оси ОХ, значит название функции (косинус)
сохраняется.
Ответ: cos ( -α) = - cos α
11. Правила: 1. Функция в правой части равенства берется с тем же знаком, какой имеет исходная функция, если 0<α<π/2. 2. Для
ПРАВИЛА:1. ФУНКЦИЯ В ПРАВОЙ ЧАСТИ
РАВЕНСТВА БЕРЕТСЯ С ТЕМ ЖЕ ЗНАКОМ,
КАКОЙ ИМЕЕТ ИСХОДНАЯ ФУНКЦИЯ,
ЕСЛИ 0<Α<Π/2.
2. ДЛЯ УГЛОВ, КОТОРЫЕ ОТКЛАДЫВАЕМ
ОТ ОСИ ОХ, ±Α, 2 ± Α НАЗВАНИЕ
ИСХОДНОЙ ФУНКЦИИ СОХРАНЯЕТСЯ.
ДЛЯ УГЛОВ, КОТОРЫЕ ОТКЛАДЫВАЕМ ОТ
ОСИ ОУ, /2±Α, 3 /2±Α НАЗВАНИЕ
ИСХОДНОЙ ФУНКЦИИ ЗАМЕНЯЕТСЯ (
СИНУС НА КОСИНУС, КОСИНУС НА
СИНУС, ТАНГЕНС НА КОТАНГЕНС,
КОТАНГЕНС НА ТАНГЕНС).
Например:
упростить sin (3 /2+α) =
1. 3 /2+α – угол IV четверти, синус – отрицательный, значит ставим «минус».
2. Угол 3 /2+α откладываем от оси ОУ, значит название функции (синус)
меняется на косинус.
Ответ: sin (3 /2+α) = - cos α
12.
Упростить:sin ( +α) =
1). +α – угол … четверти, синус в этой четверти имеет знак
…
2). Угол +α откладываем от оси …, значит название
функции (синус) …
Ответ: sin ( +α) = - sin α
cos (3 /2+α) =
1). В какой четверти угол?
2). От какой оси откладываем угол? Менять ли название
функции?
Ответ: cos (3 /2+α) = sin α
sin (3 /2-α) =
1). В какой четверти угол?
2). От какой оси откладываем угол? Менять ли название
функции?
Ответ: sin (3 /2-α) = - cos α
13.
14.
Применение формул приведения :Для вычислений:
3
2
3
2
1
2
2
2
15.
Будем считать, что угол α – угол I четверти, т.е. α˂ /2Эти формулы называются
формулами приведения.
16. Задание 1.Выразите тригонометрические функции через угол меньше 45°.
ЗАДАНИЕ 1.ВЫРАЗИТЕТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ЧЕРЕЗ
УГОЛ МЕНЬШЕ 45°.
cos123
cos 90
33 sin 33
tg174
tg 180 6 tg6
sin 168 sin 180 12 sin 12
tg 263 tg 270 7 ctg 7
ctg 380 ctg 360 20 ctg 20
cos 969 cos 270 31 sin 31
17. Задание 2. Упростите выражение.
ЗАДАНИЕ 2. УПРОСТИТЕ ВЫРАЖЕНИЕ.3 cos 3 cos 360 cos 90 sin 90
3 cos 3 cos sin sin 2 sin


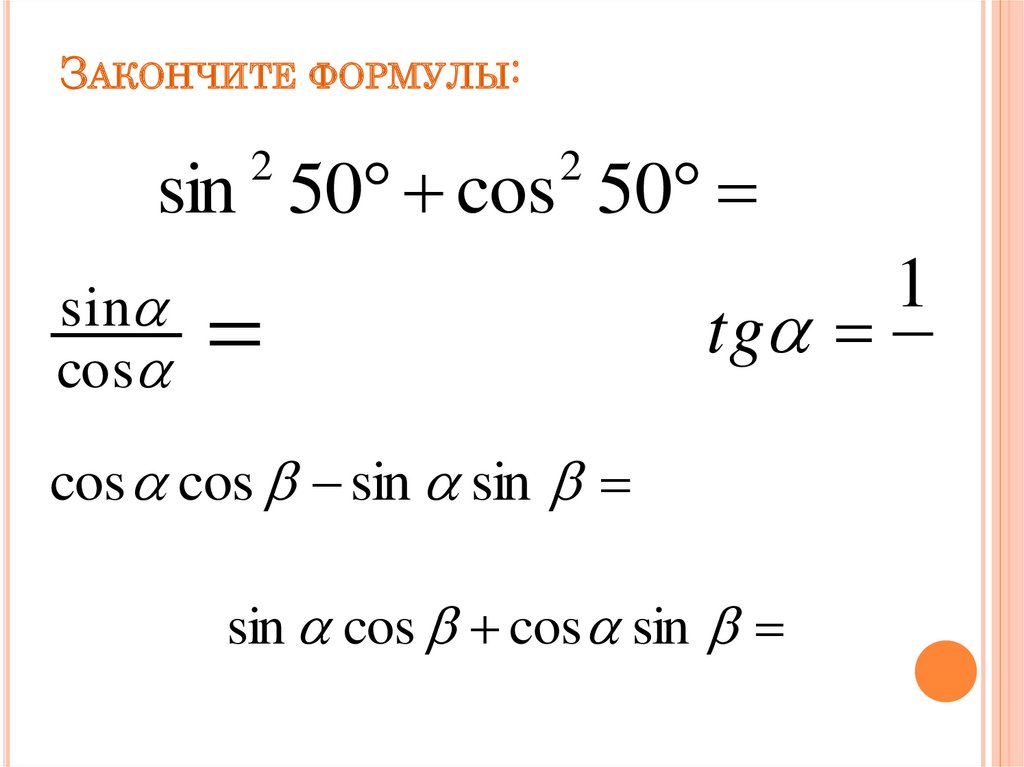









 mathematics
mathematics








