Формулы приведения

1. Формулы приведения

2. ЗАДАНИЕ

1. Повторяете с 3
ЗАДАНИЕ
по 5 слайд
2. Записать 6,7,8
3.Пример
упрощения ,слайд
№9
4.Решить №89
5. Сдаете на
следующем уроке

3.

В какой
четверти
находится
угол ?
• 1250; 3500;
2300;1850;3300
0
• -800
0
725 ;
0
72 ;

4.

Определить
знаки:
• sin 1350;
• sin (-2570); sin 8200;
• cos (-2750);
• sin 1170; cos 3850;
• tg 950; ctg (-3650);
ctg
0
78

5. Превратить в градусы:

Превратить
в градусы:
3П 3П П
; ;
;
2 4 2
7П 5П 2П
;
;
6 3 3

6.

sin(
• Формулы
• вида:
n
)
2
n
cos(
)
2
n
tg (
)
2
n
ctg (
)
2
Можно упростить, пользуясь правилом

7.

• 1.Если в формуле
Правило
содержится 900 или
2700, функция меняется
на «кофункцию»,синус
на косинус, косинус на
синус, тангенс на
котангенс, котангенс на
тангенс.
Если в формуле
содержится 1800 или
3600, то функция не
меняется

8.

ПРАВИЛО
2. В правой части
ставится тот знак
, который имела
бы левая часть
при условии,что 0
< α < П/2

9. Пример:

сos (2700 + α ) = sin α
Пример:
В левой части имеем 2700,
по первому правилу
меняем сos на sin. Знак
определяем по левой
части, а ставим его в
правую.
2700 + α – это 4 четверть. В
ней косинус(НЕ СИНУС)
имеет знак плюс.Знаки на
слайдах №11,12,13

10.

ПРИМЕР
tg ( 1800 - α ) = - tg α
В формуле 180
градусов. По
первому правилу,
тангенс не
меняем.Четверть
вторая .Знак
тангенса минус.
Ставим его в
правую часть

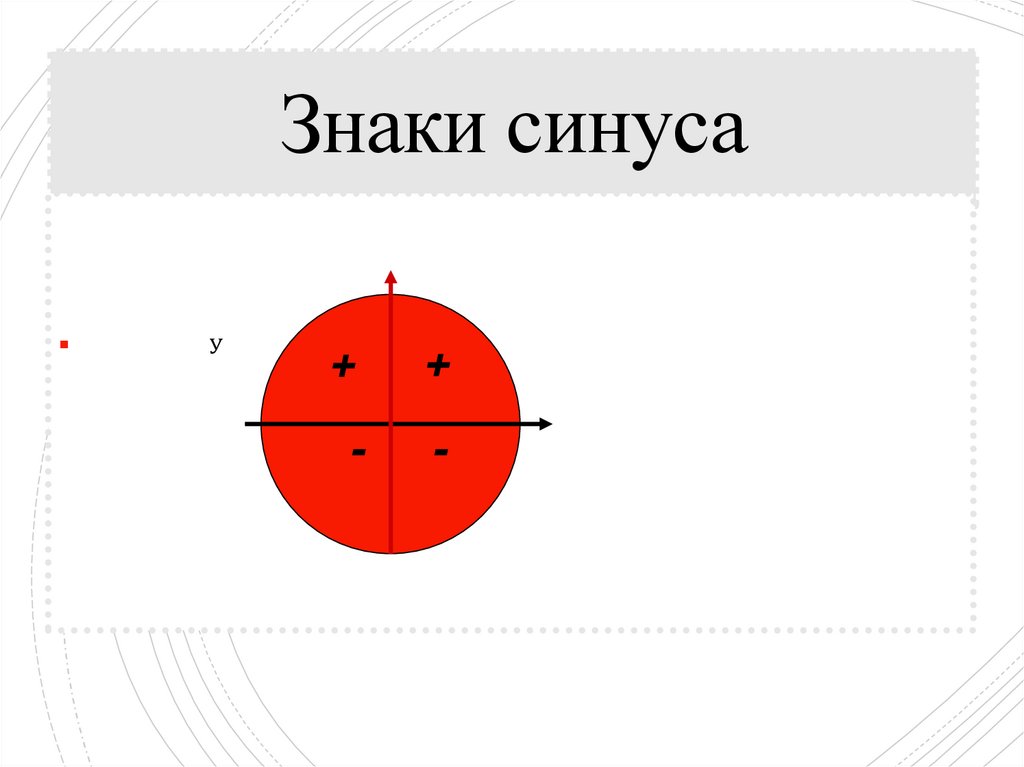
11. Знаки синуса

У
х
+
+
-
-

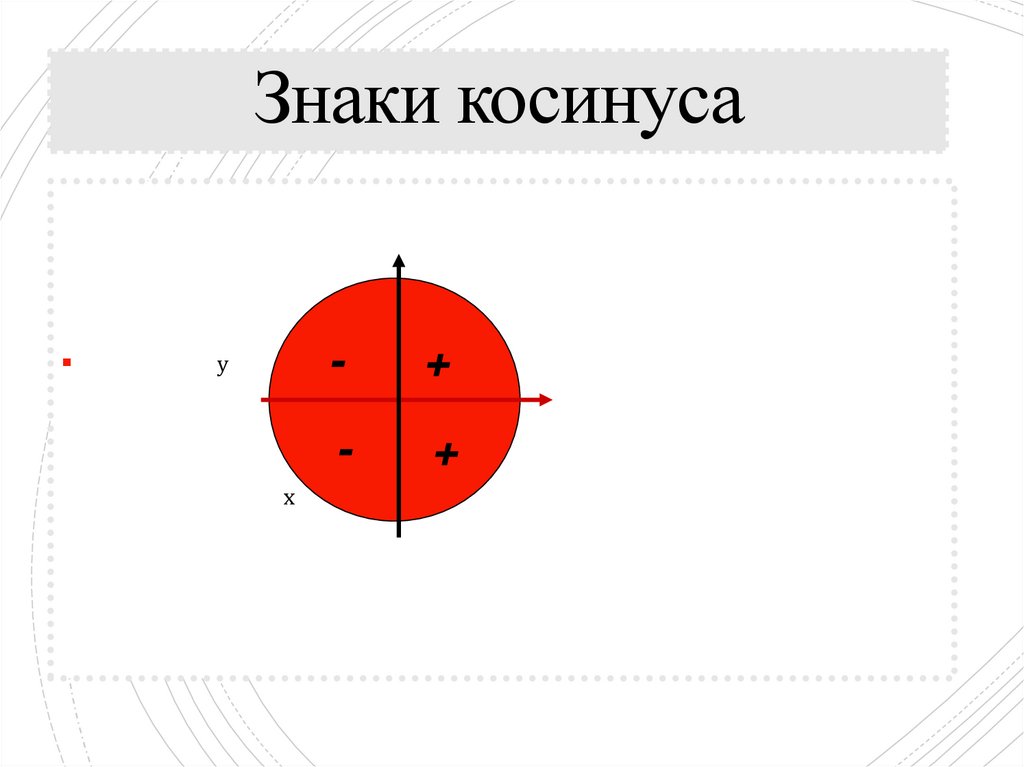
12. Знаки косинуса

у
х
-
+
-
+

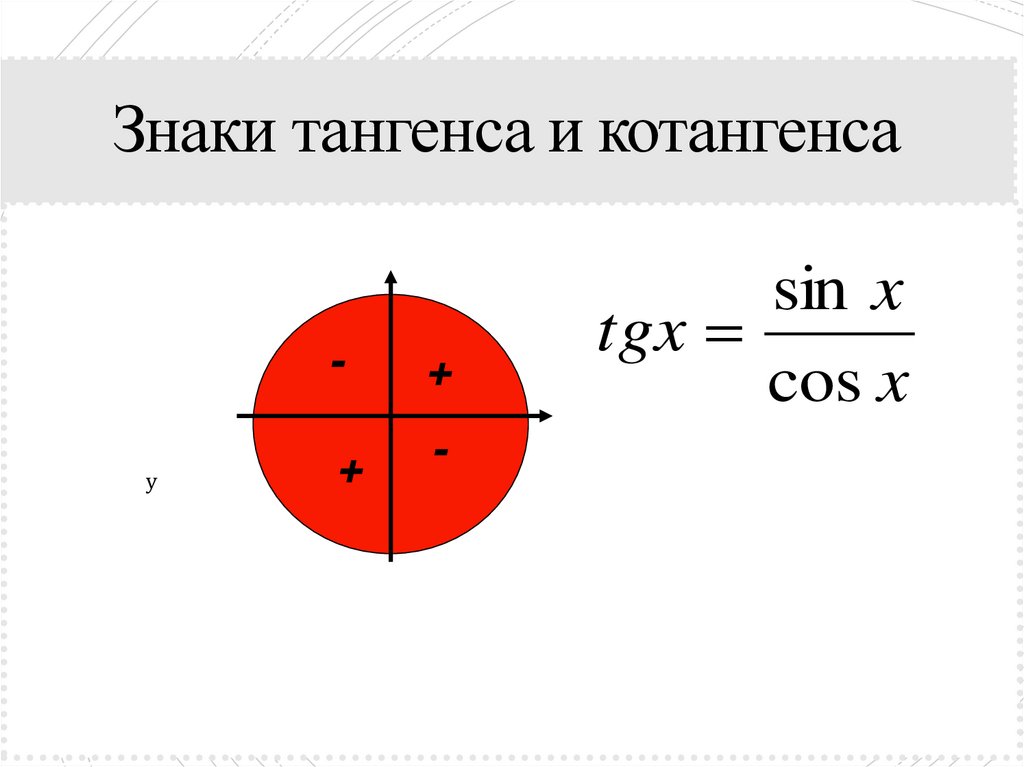
13. Знаки тангенса и котангенса

у
-
+
+
-
sin x
tgx
cos x