Механика кинематика

1.

МЕХАНИКА
КИНЕМАТИКА
«Это очень просто, мои
дорогие: потому что
политика гораздо сложнее,
чем физика».
А. Эйнштейн
© Парфентьева Наталия Андреевна

2.

Храм лотоса, Индия
Кибертектурное Яйцо.
Мумбай, Индия
Китайский национальный театр в Пекине

3.

Храм лотоса, Китай
Спиралевидная башня, Тулуза, Франция
Сооружение Кугген, Гетеборг, Швеция

4.

Физика – природа. Аристотель (IV век до н.э.).
М.В. Ломоносов перевод «Вольфианская экспериментальная физика» (1746).
Первый учебник по физике – П.И. Страхов «Краткое начертание физики» (1810).
Метод: наблюдение – предположение (теория) – эксперимент.
Модели в физике – физическая, математическая.
Физические величины.
Физические законы – связь между физическими величинами.
Открытия в физике.
Физика и другие науки, физика и техника.

5.

Модели в физике. Виды движения
Материальной точкой называется тело, размерами и формой
которого можно пренебречь в условиях данной задачи, таким
образом движение реального тела можно рассматривать как
движение геометрической точки.
Абсолютно твердым телом называется тело, расстояние
между любыми двумя точками которого остается постоянным
при его движении.

6.

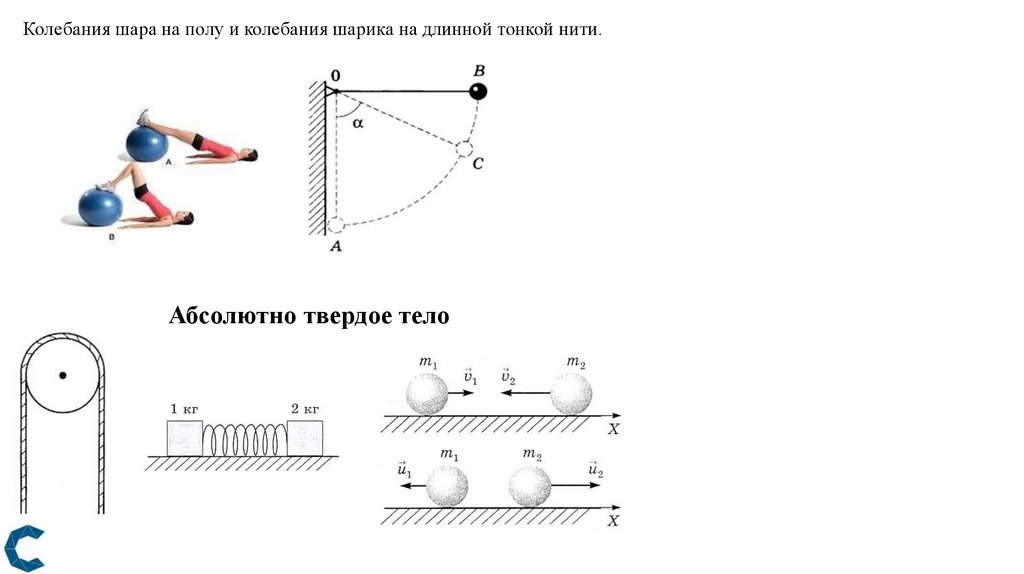
Колебания шара на полу и колебания шарика на длинной тонкой нити.
Абсолютно твердое тело

7.

Механическим движением называется изменение положения
тела или его частей относительно других тел с течением времени.
Всякое движение относительно. Характер движения зависит
от того, относительно каких тел мы рассматриваем данное движение.
Тело, относительно которого мы рассматриваем положение
других тел в пространстве, называется телом отсчета.
Системой отсчета называют
систему координат, связанную
с телом отсчета, и выбранный
метод отсчета времени, т.е. часы.
Выбор системы отсчета зависит
от условий данной задачи.

8.

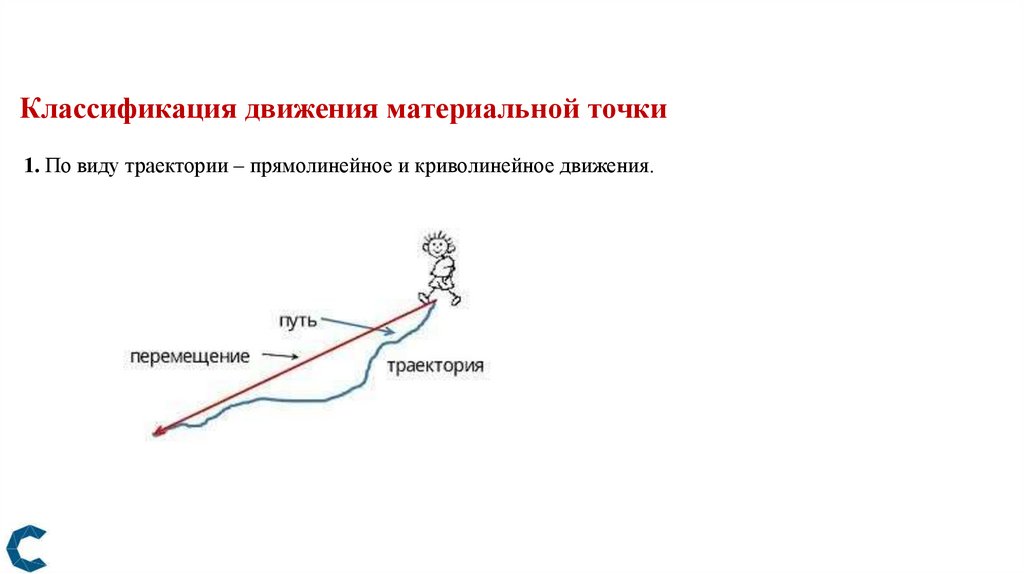
Классификация движения материальной точки
1. По виду траектории – прямолинейное и криволинейное движения.

9.

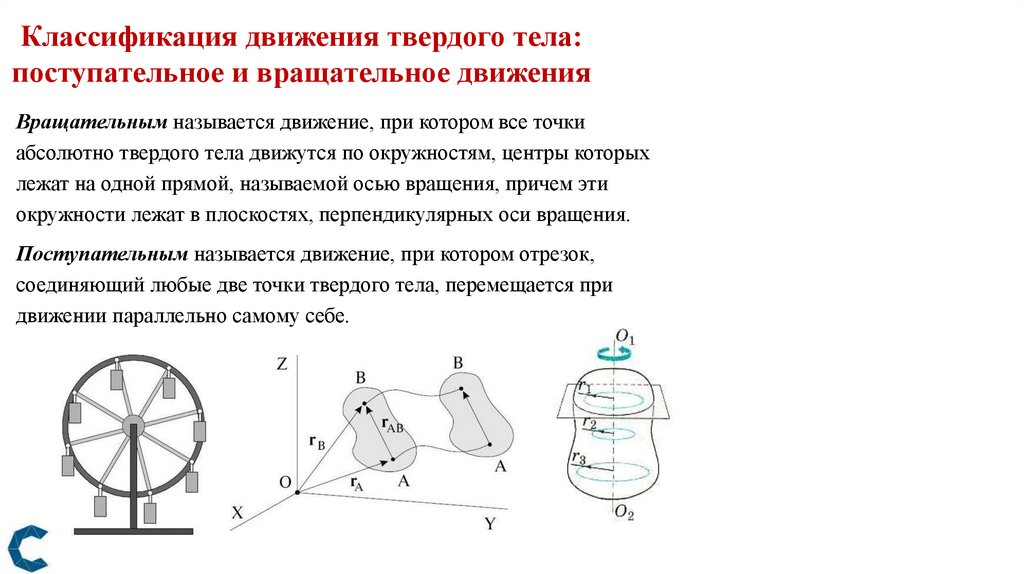
Классификация движения твердого тела:
поступательное и вращательное движения
Вращательным называется движение, при котором все точки
абсолютно твердого тела движутся по окружностям, центры которых
лежат на одной прямой, называемой осью вращения, причем эти
окружности лежат в плоскостях, перпендикулярных оси вращения.
Поступательным называется движение, при котором отрезок,
соединяющий любые две точки твердого тела, перемещается при
движении параллельно самому себе.

10.

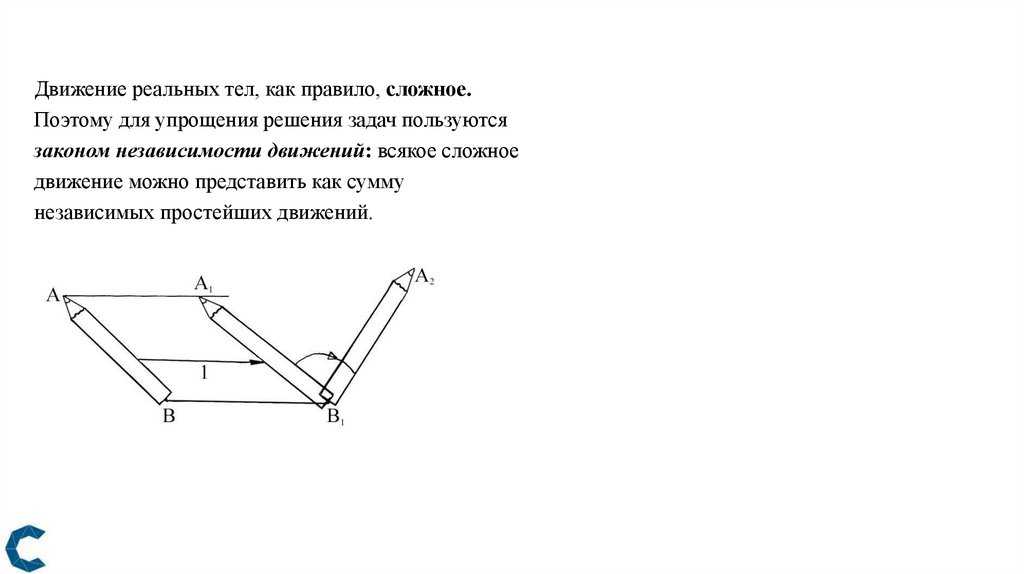
Движение реальных тел, как правило, сложное.
Поэтому для упрощения решения задач пользуются
законом независимости движений: всякое сложное
движение можно представить как сумму
независимых простейших движений.

11.

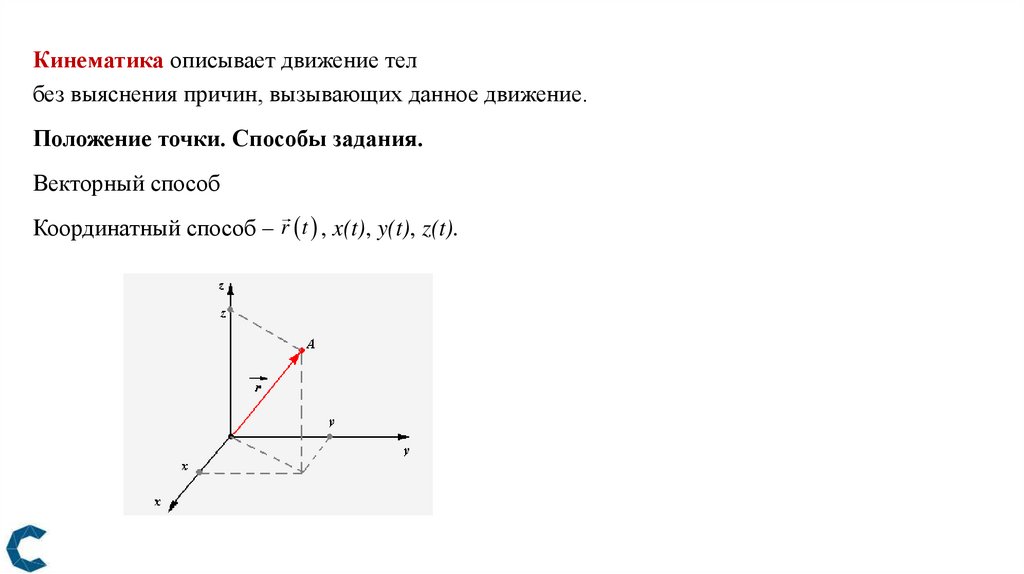
Кинематика описывает движение тел
без выяснения причин, вызывающих данное движение.
Положение точки. Способы задания.
Векторный способ
Координатный способ – r t , x(t), y(t), z(t).

12.

Основная задача кинематики – написать уравнение движения,
обратная задача – по уравнению движения определить
кинематические характеристики.
Что значит написать уравнение движения?
Задать положение точки и найти изменение этого положения со
временем.
1. Выбор системы отсчёта и системы координат – простота
описания движения и одновременно возможность ответа на вопрос
задачи.
«Свобода творчества – свобода делать ошибки». П. Капица
2. Записать уравнение движения.
3. Используя уравнение движение, ответить на вопросы задачи.
Умение решать задачи – лучшее доказательство
понимания законов физики.

13.

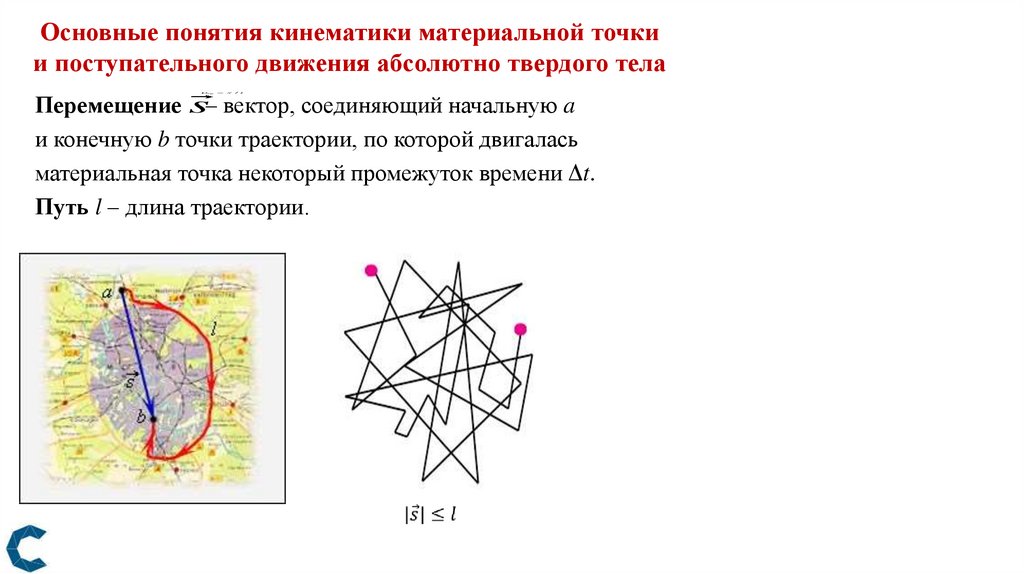
Основные понятия кинематики материальной точки
и поступательного движения абсолютно твердого тела
Перемещение s– вектор, соединяющий начальную a
и конечную b точки траектории, по которой двигалась
материальная точка некоторый промежуток времени Δt.
Путь l – длина траектории.
ср
s
/ t

14.

Средняя скорость прохождения пути – скалярная величина,
равная отношению пути к промежутку времени, за который
этот путь пройден.
vср l = l / t.
Средняя скорость, равная отношению перемещения к
промежутку времени, за которое это перемещение произошло:
vср s / t
Мгновенная скорость – скорость в данный момент времени.
Мгновенная скорость всегда
направлена по касательной
к траектории в данной точке.

15.

Задача. Турист прошел L1 = 10 км на север за t1 = 2 ч,
затем изменил направление движения и двигался на восток
со скоростью υ2 = 4 км/ч, пройдя L2 =12 км.
Найдите средние скорости движения и перемещения туриста.
Решение.
L
vср
t
L s1 s2
vср
t t1 t2 t2 t1
s1 s2
t
s2
v2
vср s1 s2 / t1 s2 / v2 4, 4 км / ч.

16.

Мгновенная скорость – скорость
в данный момент времени.
Δr
vмгн = v = lim
= r
Δt 0 Δt
уравнение движения
t2
r t v(t )dt
t1
t2
dx
vx
x v x dt
dt
t1

17.

Прямолинейное равномерное движение
t
v x сonst
x x0 v x dt v x t x(t ) x0 v xt
0

18.

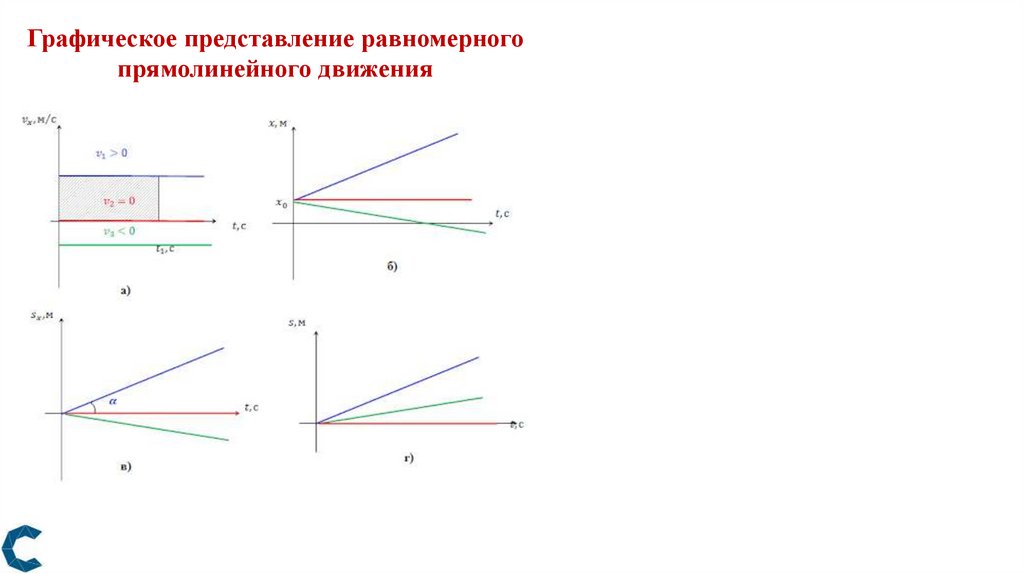
Графическое представление равномерного
прямолинейного движения

19.

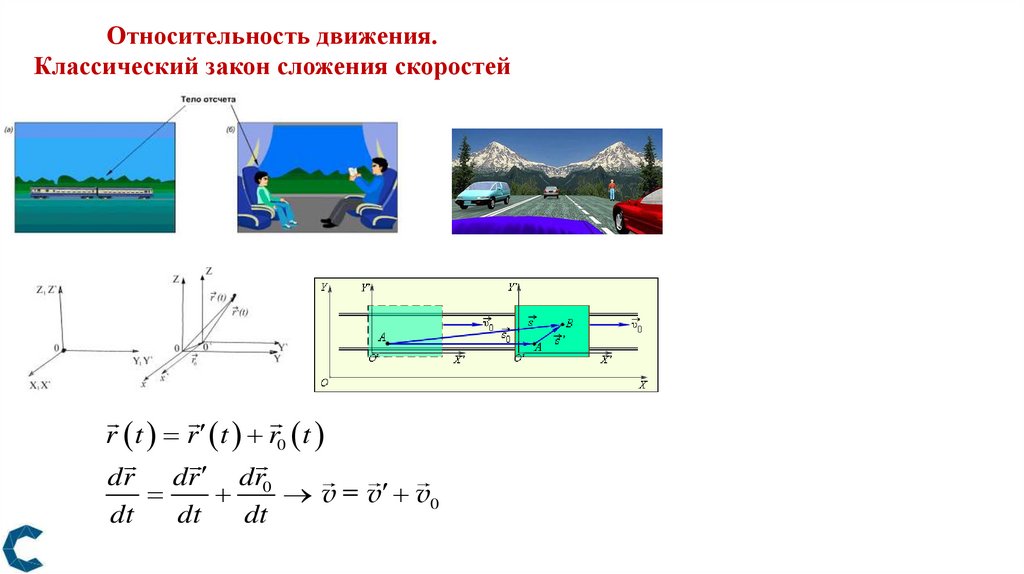
Относительность движения.
Классический закон сложения скоростей
r t r t r0 t
dr dr dr0
v = v v0
dt
dt
dt

20.

Классический закон сложения скоростей
vабс vотн vпер
v vабс абсолютная скорость,
скорость тела относительно неподвижной системы отсчета
v vотн – относительная скорость,
скорость тела относительно подвижной системы отсчета;
v0 vпер – переносная скорость,
скорость подвижной системы отсчета
относительно неподвижной.
Абсолютная скорость тела равна
геометрической сумме векторов
относительной и переносной скоростей.

21.

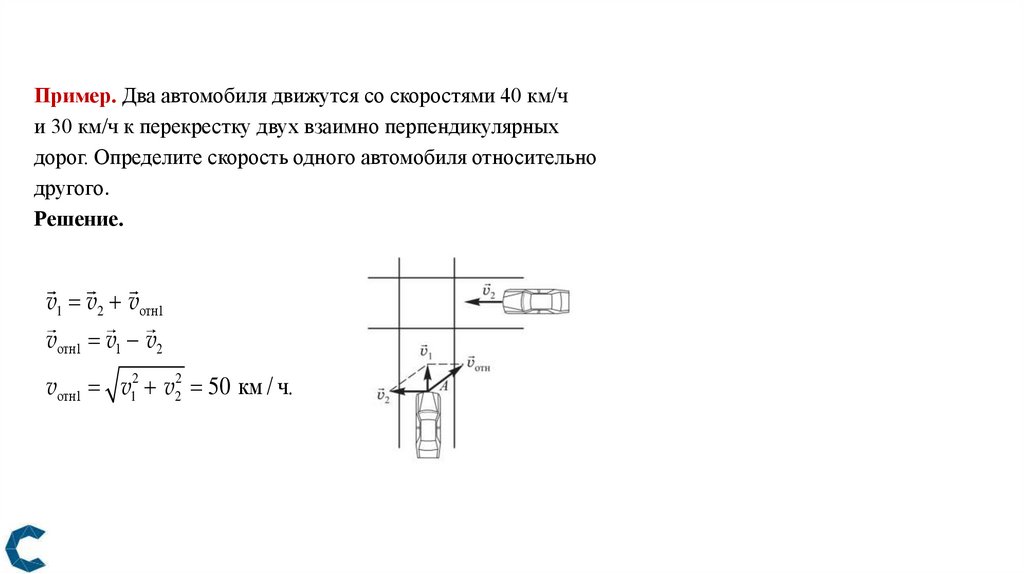
Пример. Два автомобиля движутся со скоростями 40 км/ч
и 30 км/ч к перекрестку двух взаимно перпендикулярных
дорог. Определите скорость одного автомобиля относительно
другого.
Решение.
v1 v2 vотн1
vотн1 v1 v2
vотн1 v12 v22 50 км / ч.

22.

Движение с переменной скоростью. Ускорение
Среднее ускорение определяется отношением изменения скорости
к промежутку времени, за который это изменение произошло :
aср v / t.
Мгновенное ускорение – ускорение тела в данный момент времени.
Это физическая величина, равная пределу отношения изменения
скорости к промежутку времени, за который это изменение произошло,
при стремлении промежутка времени к нулю :
a мгн
v
v .
lim
t 0 t

23.

a полное ускорение
аτ – тангенциальное (ак – касательное) ускорение, направлено
по касательной к траектории и характеризует изменение скорости по модулю.
аn – нормальное (ацс – центростремительное) направлено к центру кривизны
траектории по нормали к скорости , характеризует изменение скорости
по направлению, аn = v 2 / R, где – мгновенная скорость,
R – радиус кривизны траектории в данной точке.
Модуль мгновенного ускорения равен
a мгн a 2 an2 .

24.

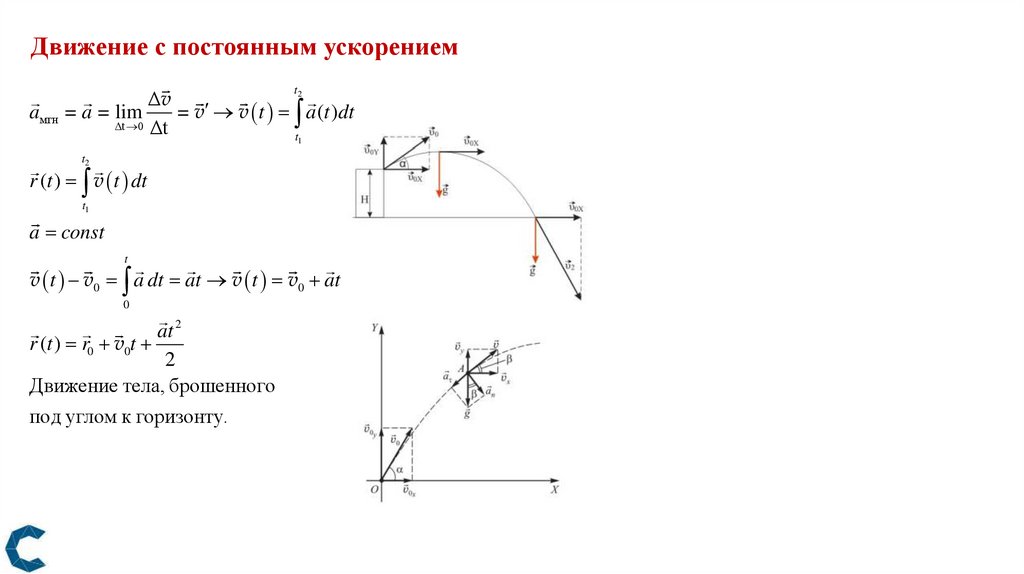
Движение с постоянным ускорением
t
aмгн
2
Δv
= a = lim
= v v t a (t )dt
Δt 0 Δt
t1
t2
r (t ) v t dt
t1
a const
t
v t v0 a dt at v t v0 at
0
at 2
r (t ) r0 v0t
2
Движение тела, брошенного
под углом к горизонту.

25.

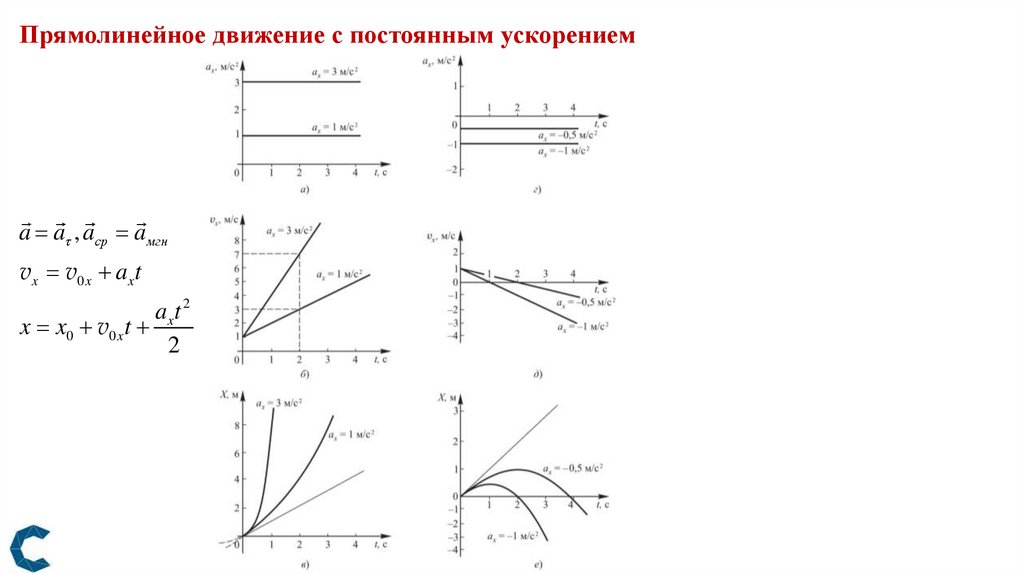
Прямолинейное движение с постоянным ускорением
a a , aср a мгн
v x v0 x a x t
ax t 2
x x0 v0 x t
2

26.

Свободное падение тел (прямолинейное движение)
Мяч бросили вертикально вверх со скоростью v0 = 5 м/с
с высоты h = 1,5 м. Определите: 1) время полета мяча до его
падения на землю tпол; 2) максимальную высоту подъема hmax;
3) конечную скорость υк.
v y = v0 gt
gt 2
gt 2
у h v0t –
у h v0t –
2
2
2
gtпол
0 h v0tпол –
2
tпол
hmax
v0 v02 2 gh
g
0 = v0 gtпод tпод
v02
h
2g
vку v0 – gtпол v02 2 gh 7, 4 м / с.
v0
g

27.

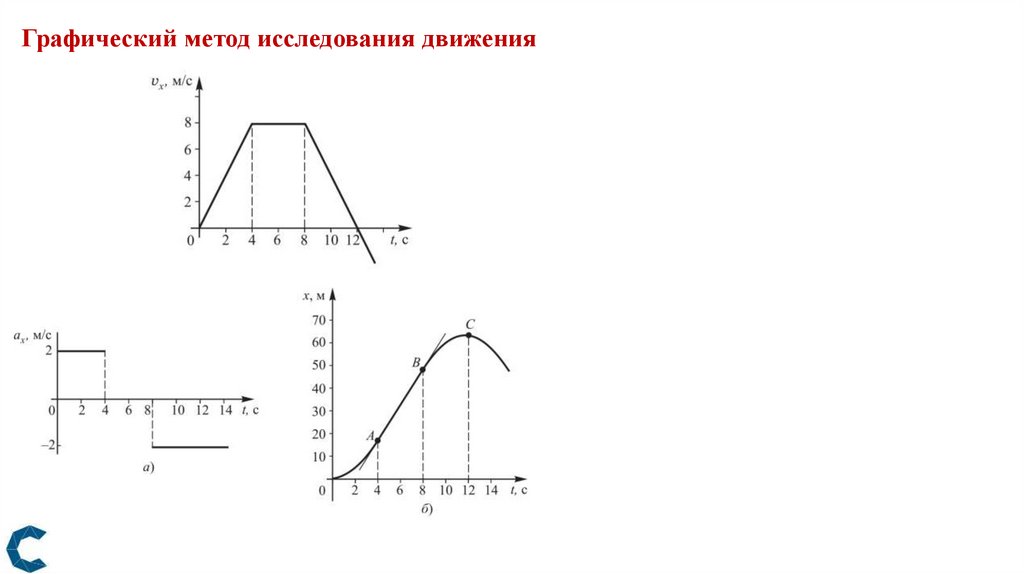
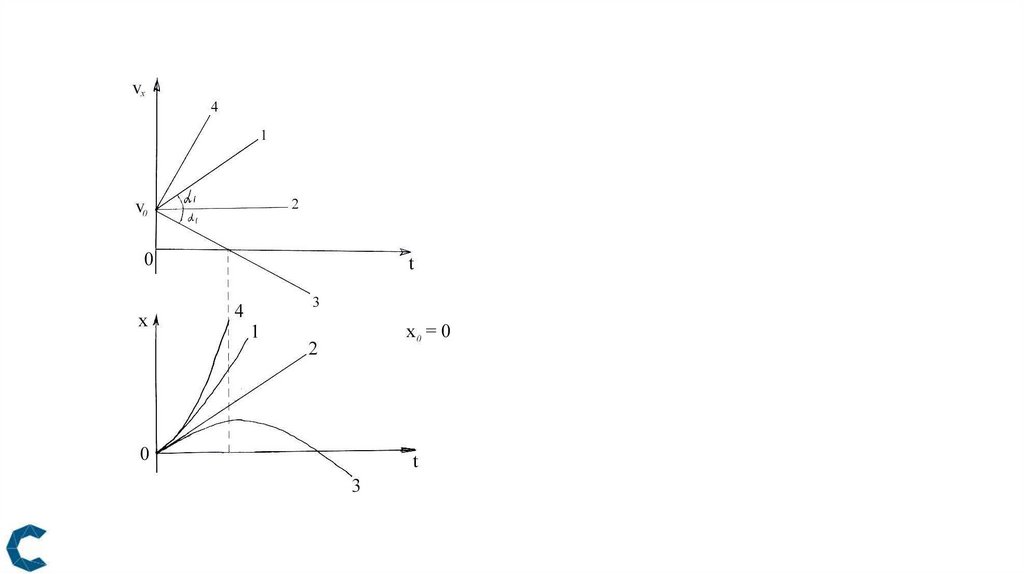
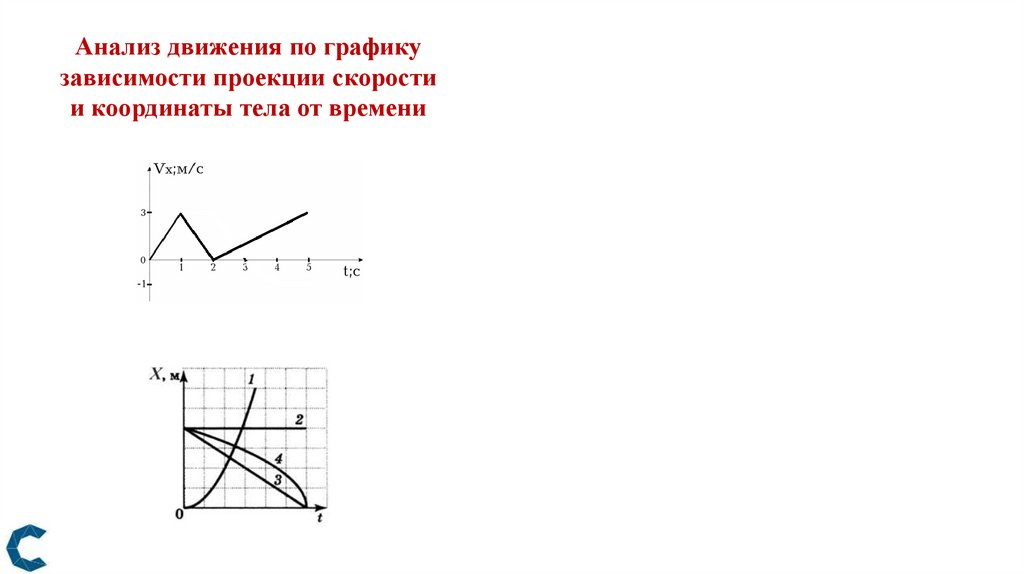
Графический метод исследования движения

28.

29.

Анализ движения по графику
зависимости проекции скорости
и координаты тела от времени

30.

Рис. 1
0-1 с – равноускоренное движение
с ускорением 3 м/с2
1-2 с – равноускоренное движение
с ускорением – 3 м/с2
2-5 с – равноускоренное движение
с ускорением – 1 м/с2
Рис. 2
1 – равноускоренное движение.
2 – тело неподвижно.
3 – равномерное движение
со скоростью, направленной
в сторону, противоположную оси ОХ.
4 – равноускоренное движение
со скоростью и ускорением,
направленными в сторону,
противоположную оси ОХ.

31.

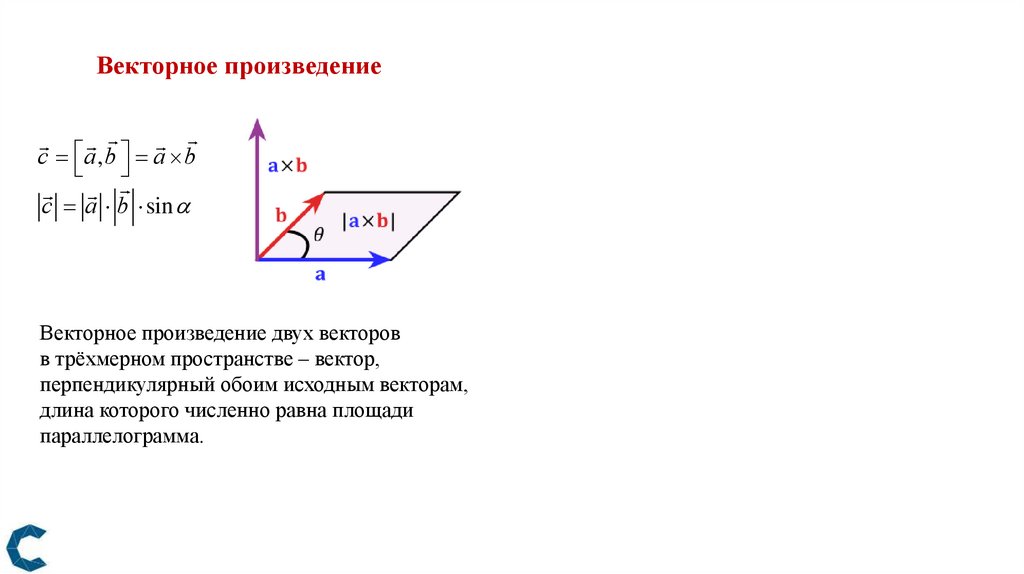
Векторное произведение
с a , b a b
с a b sin
Векторное произведение двух векторов
в трёхмерном пространстве – вектор,
перпендикулярный обоим исходным векторам,
длина которого численно равна площади
параллелограмма.

32.

Основные кинематические характеристики
и уравнения вращательного движения
2 – 1
s1 s2
t уравнение движения
При равномерном движении по окружности
0
0 t ,
t
φ 0 – начальный угол между радиусом
ω / t
– вектором и осью OX
s r v = r
угловая скорость,векторная величина
v r
0 t
2
2 r
v
.
T
T

33.

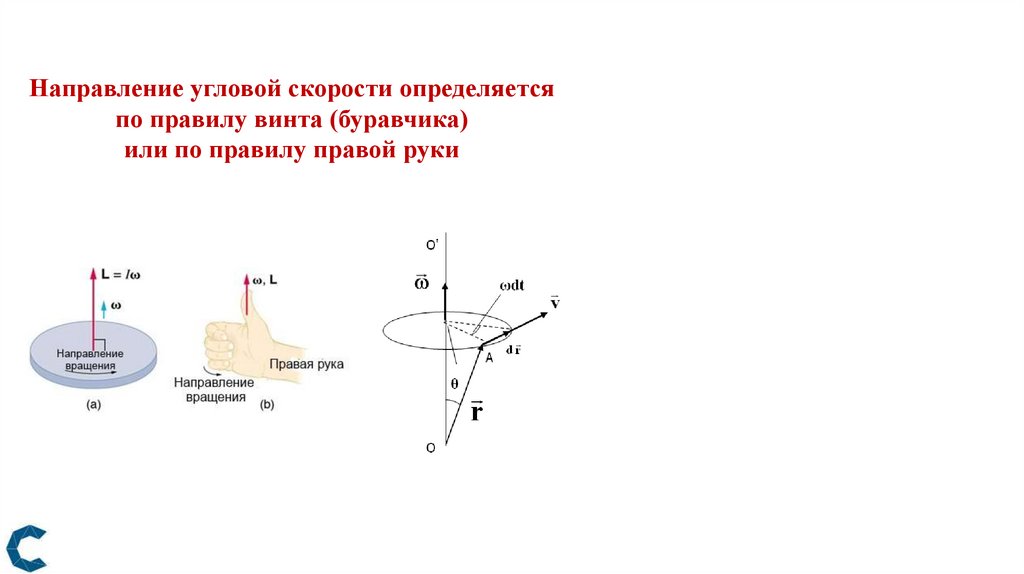
Направление угловой скорости определяется
по правилу винта (буравчика)
или по правилу правой руки

34.

Пример. Колесо катится со скоростью v. Определите
скорость верхней точки обода колеса А, а также точек
В и С относительно дороги. Радиусы R и r известны.
v0 / R
v A 2 R 2 v0
R r
v B r R v0
.
R
Пример. Ускорение спутника на высоте 200 км
от поверхности Земли равно 9,2 м/с2. Определите
скорость спутника и период обращения спутника.
v2
an
v an r 7,8км / с
r
4 2
r
an 2 r T 2
88мин.
T
an

35.

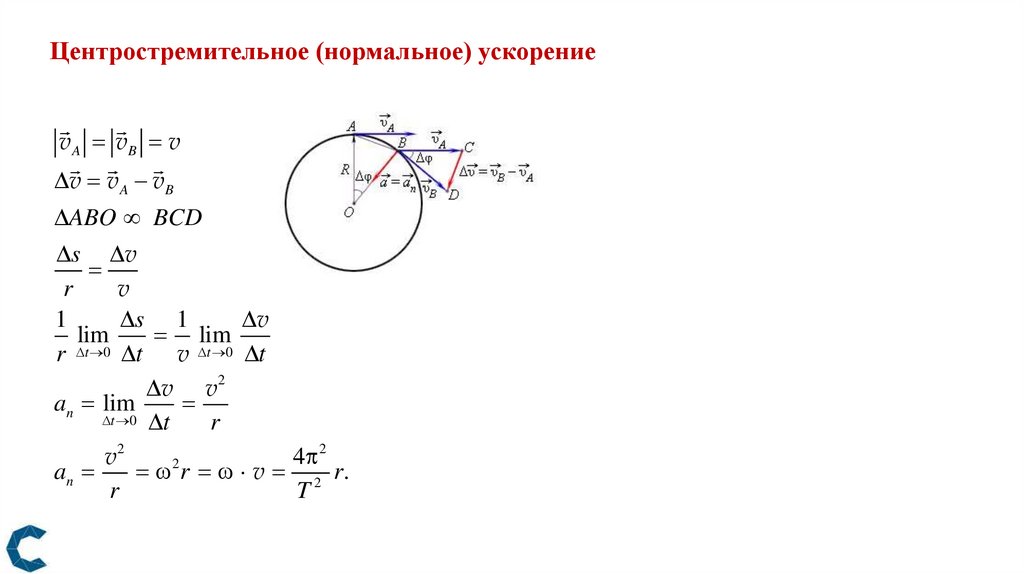
Центростремительное (нормальное) ускорение
v A vB v
v v A vB
ABO BCD
s v
r
v
1
s 1
v
lim
lim
t
0
r
t v t 0 t
v v 2
an lim
t 0 t
r
v2
4 2
2
an
r v 2 r.
r
T

36.

Угловое ускорение
d
lim
2 1
t 0 t
dt
Ось вращения и радиус постоянны
v
( r )
a lim
lim
r lim
r
t 0 t
t 0
t
0
t
t
a ε r = ε r

37.

Связь линейных и угловых
кинематических характеристик
S r
d S d r
S
r
v r v r
t
t
a r a r

38.

Движение тела, брошенного под углом к горизонту
Задача. Тело брошено под углом к горизонту. Даны начальная скорость
и угол. Определим: 1) уравнение движения; 2) траекторию движения;
3) время полета tп; 4) дальность полета l; 5) максимальную высоту
подъема hmax; 6) an и a в начальной точке траектории и в наивысшей
точке подъема; 7) радиусы кривизны траектории в этих точках.
Решение.
gt 2
1) r t = v0 t +
2
х v0 xt v0tcos ,
y v0 yt – gt 2 / 2 v0tsin – gt 2 / 2
v y v0 y – gt.
gx 2
2) y x tg – 2
.
2
2 v0 cos

39.

3) y t ( v0sinα – gt / 2) 0
t1 0, t2
2v0 / g sinα
v02 sin 2α
4) xmax l v0 xtп ( v0cosα · 2 v0sinα) / g
g
5)tпод tпад tп / 2
ymax hmax
2
2
v
gtпо
v02 sin 2 α
0y
д
v0 y tпод –
.
2
2g
2g
В точке О : a0t g sin , a0 n g cos .
v02
R0
g cos α
В точке А: v y 0
v A v0 x v0cos
v02 cos 2 α
RA
.
g
an g