Статистические приемы изучения взаимосвязи явлений

1. Статистические приемы изучения взаимосвязи явлений

2.

Вопрос 1. Понятие о статистической связи
КРА как общее понятие позволяет решать следующие задачи:
изучение тесноты связи между двумя и более переменными;
определение направления связи;
установление аналитического выражения (формы) взаимосвязи между
явлениями;
определение возможных ошибок показателей тесноты связи и параметров
уравнений регрессии.

3.

• В статистике различают два вида связи:
• Функциональные связи характеризуют изменение одного явления под
влиянием другого или других. Эта связь считается жестко
детерминированной, и она характеризуется для всех единиц совокупности в
равной мере.
• Корреляционные (стохастические) связи между явлениями проявляются
только в среднем для совокупности и характеризуют вариацию
результативного признака вследствие вариации факторных признаков.
Корреляционные связи – это неполные связи, т.е. такие, которые отражают
влияние одного или нескольких факторов.

4.

• Функциональные и статистические зависимости между
переменными величинами могут быть прямыми и
обратными. Если изменения результативного признака
совпадают с направлением изменения признака-фактора,
то такая связь называется прямой.
• И наоборот, если рост признака-фактора приводит к
уменьшению результативного признака, то такая связь –
обратная.

5.

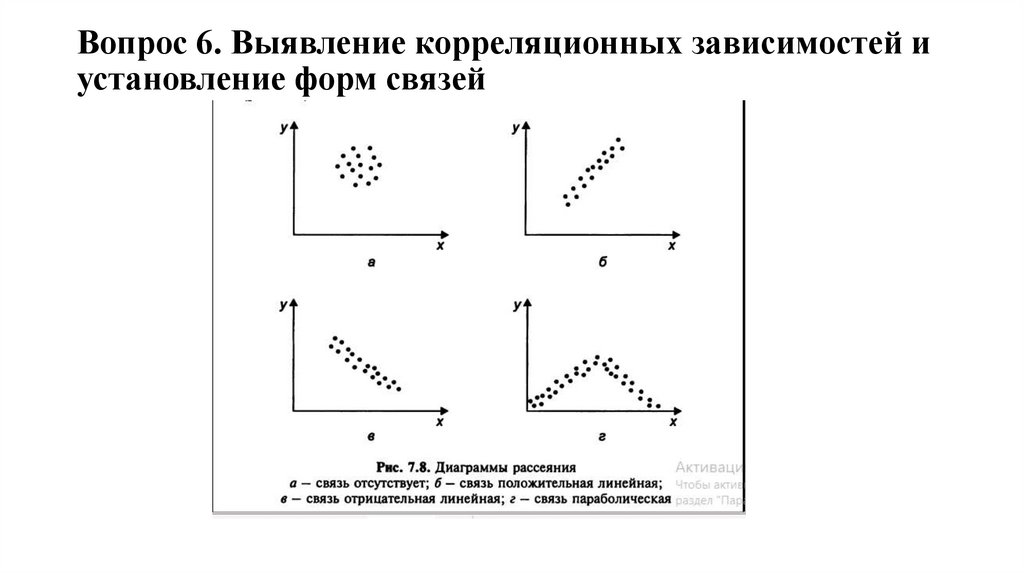
• Связи могут быть линейными или нелинейными. Если
статистическая зависимость между признаком-фактором
и результативным признаком может быть приближенно
представлена уравнением прямой линии, то ее называют
линейной связью.
• Если связь между факторным и результативным
признаками представлена в виде параболической,
гиперболической, степенной, показательно или иной
функции, то такие зависимости называются нелинейными.

6.

• Рассматривая связь средней величины результативного
признака у с изменением одного признака-фактора х,
получим возможность определить наличие парной
корреляции.
• Если на результативный признак оказывают влияние два
или более факторных признака, то будем вычислять
наличие множественной корреляции.

7. Вопрос 2. Метод параллельных рядов

• Если
наблюдаемая
статистическая
совокупность
представлена небольшим числом исходных данных, то
наличие или отсутствие корреляции между х и у можно
определить методом параллельных рядов.
• С этой целью значения факторного признака х
располагают по мере возрастания или убывания, затем
ранжированные
значения
х
сопоставляют
с
результативным признаком у.

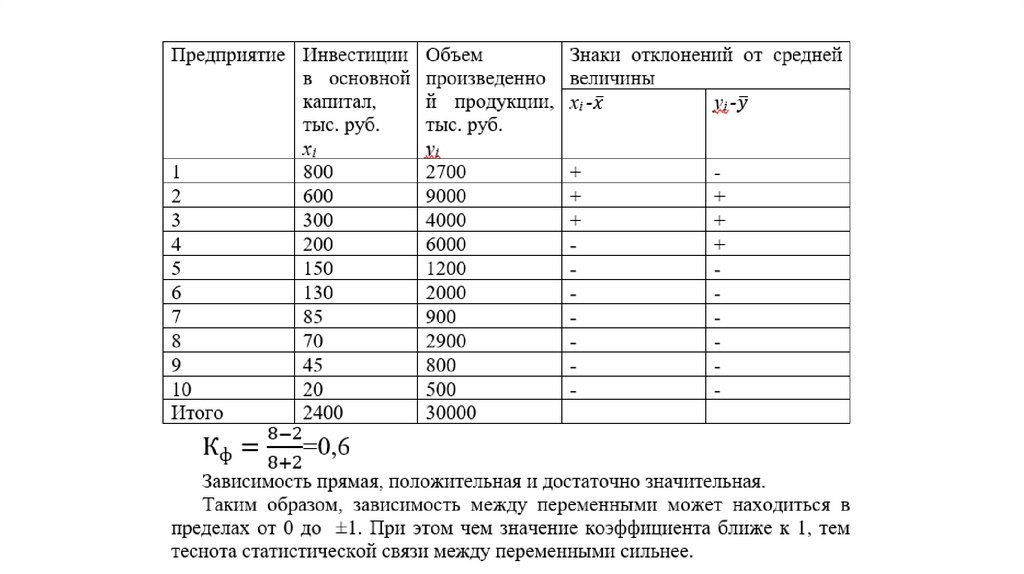
8.

Предприятие
1
2
3
4
5
6
7
8
9
10
Итого
Инвестиции
в Объем
основной
произведенной
капитал,
тыс. продукции, тыс.
руб., xi
руб., yi
800
2700
600
9000
300
4000
200
6000
150
1200
130
2000
85
900
70
2900
45
800
20
500
2400
30000

9.

• Коэффициент
знаков)
• Кф =
Фехнера
(коэффициент
σ С−σ Н
σ С+σ Н
• где σ С – число совпадения знаков;
• σ Н – число несовпадения знаков.
совпадения

10.

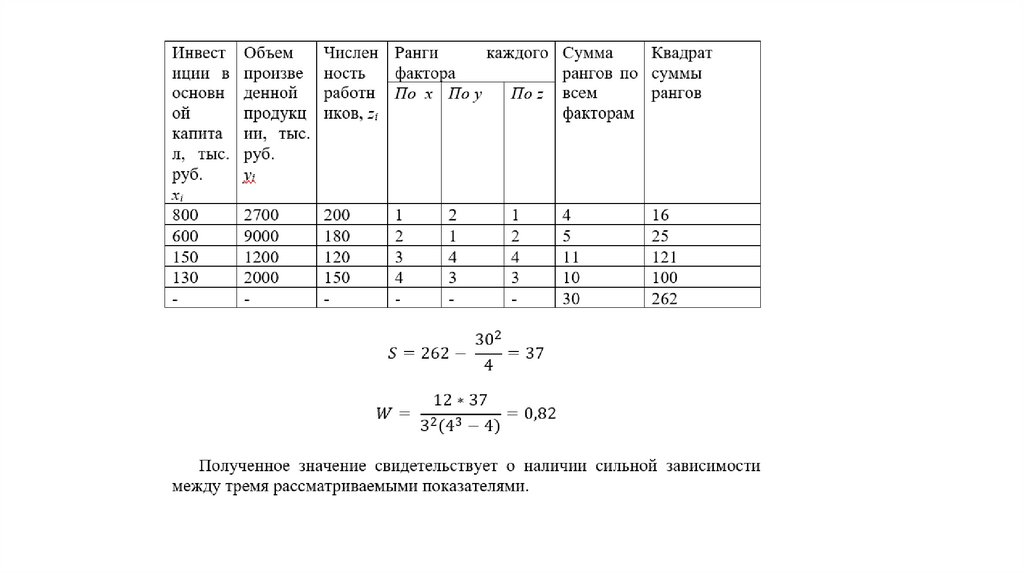
11.

Вопрос 3. Коэффициент корреляции рангов
Ранг – это порядковый номер, который присваивается каждому
индивидуальному значению признаку х и у отдельно после их
упорядочения по возрастанию или убыванию.
Коэффициент корреляции рангов определяется по формуле:
6 σ