Similar presentations:
Статистическое изучение взаимосвязи социально-экономических явлений
1.
СТАТИСТИКААналитическая статистика.
Лекция 3. Статистическое изучение взаимосвязи
социально-экономических явлений.
Автор: Равичев Л.В.
РХТУ им. Д.И.Менделеева
Кафедра управления технологическими инновациями
Москва - 2013
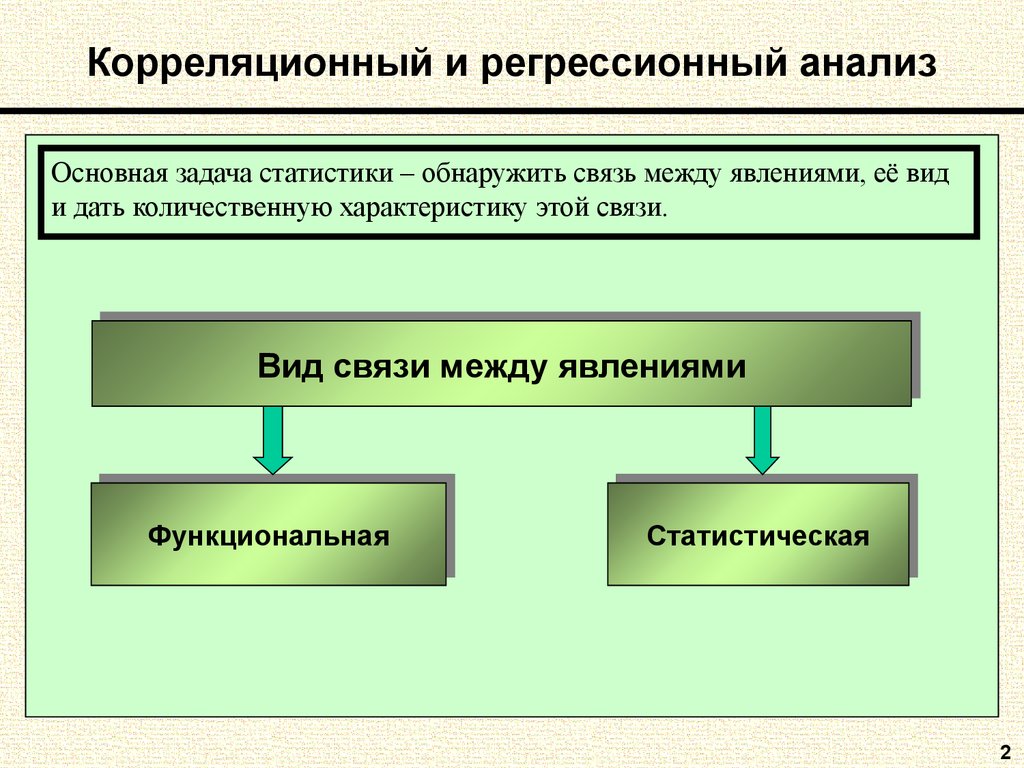
2. Корреляционный и регрессионный анализ
Основная задача статистики – обнаружить связь между явлениями, её види дать количественную характеристику этой связи.
Видсвязи
связимежду
междуявлениями
явлениями
Вид
Функциональная
Функциональная
Статистическая
Статистическая
2
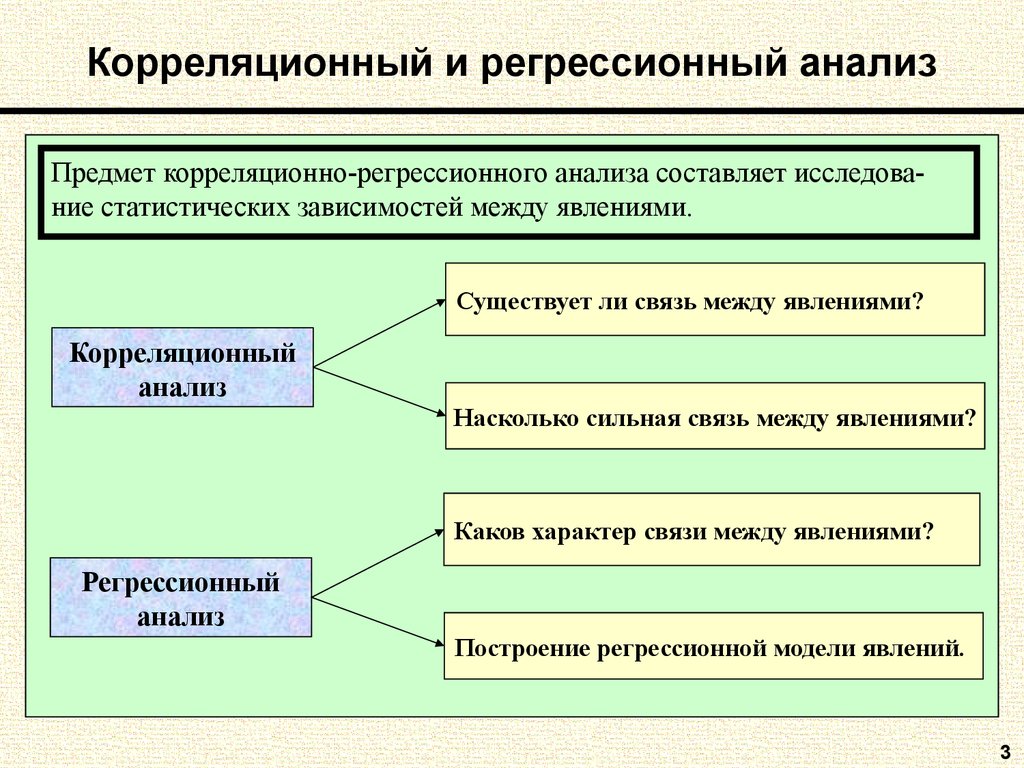
3. Корреляционный и регрессионный анализ
Предмет корреляционно-регрессионного анализа составляет исследование статистических зависимостей между явлениями.Существует ли связь между явлениями?
Корреляционный
анализ
Насколько сильная связь между явлениями?
Каков характер связи между явлениями?
Регрессионный
анализ
Построение регрессионной модели явлений.
3
4. Корреляционный анализ Диаграмма рассеяния
Простейшим приемом при исследовании зависимости между двумя количественными признаками является построение диаграммы рассеяния.Пример 1. Построить диаграмму рассеяния для результатов наблюдения
за возрастом и артериальным давлением группы людей, приведенных в
таблице.
№
Возраст, Давление,
лет (x) мм.рт.ст. (y)
1
43
128
2
48
120
3
56
135
4
61
143
5
67
141
6
70
152
4
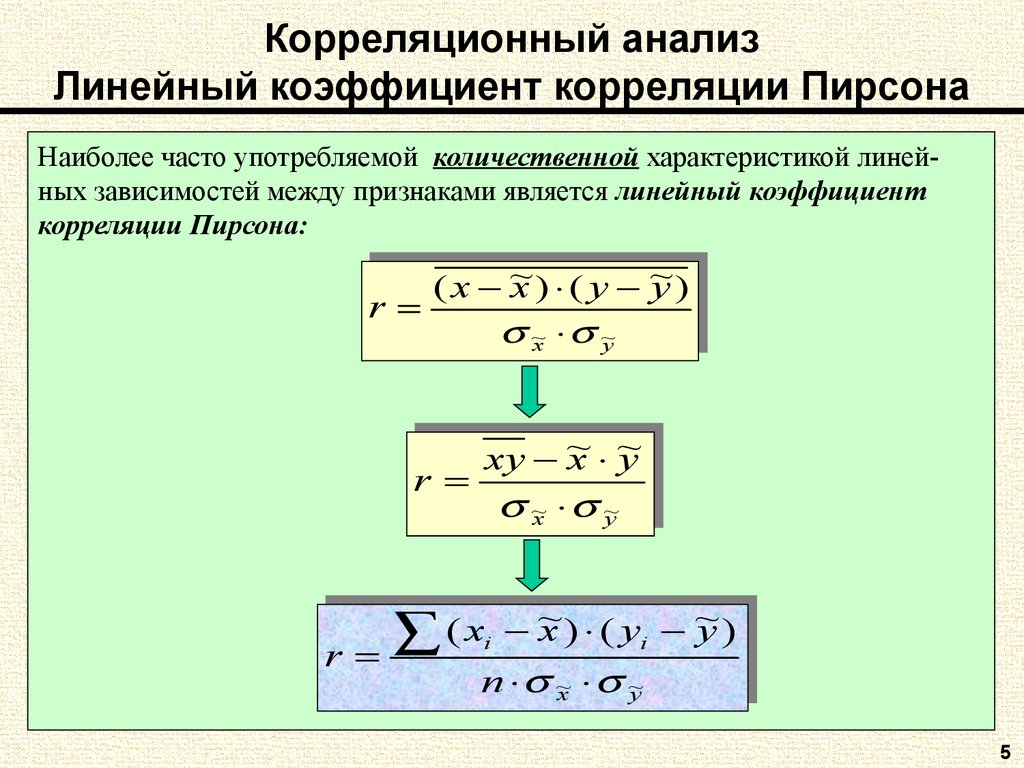
5. Корреляционный анализ Линейный коэффициент корреляции Пирсона
Наиболее часто употребляемой количественной характеристикой линейных зависимостей между признаками является линейный коэффициенткорреляции Пирсона:
~
~
~
~
(
x
x
)
(
y
y))
(
x
x
)
(
y
y
rr
~x~x
~y~y
~
~
~
~
xy
x
xy x yy
r
r
~x~x
~y~y
~
~
~
~
(
x
x
)
(
y
y))
i x ) ( yi i y
(
x
i
rr
~~x
~~y
nn
x
y
5
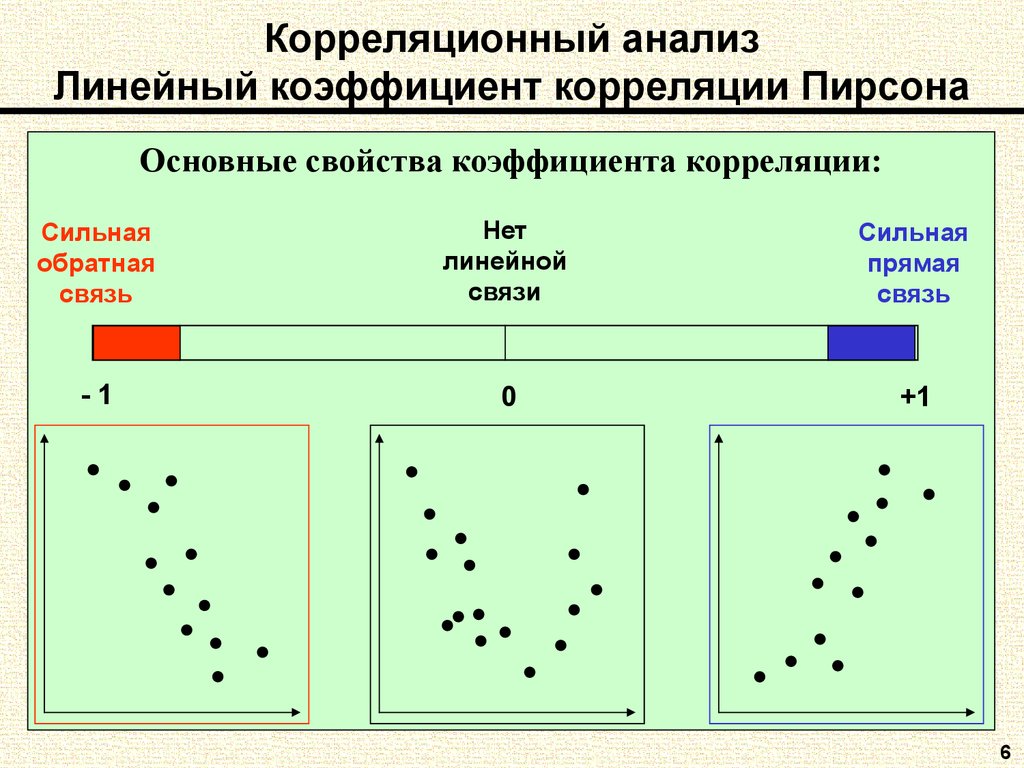
6. Корреляционный анализ Линейный коэффициент корреляции Пирсона
Основные свойства коэффициента корреляции:Сильная
обратная
связь
Нет
линейной
связи
Сильная
прямая
связь
-1
0
+1
6
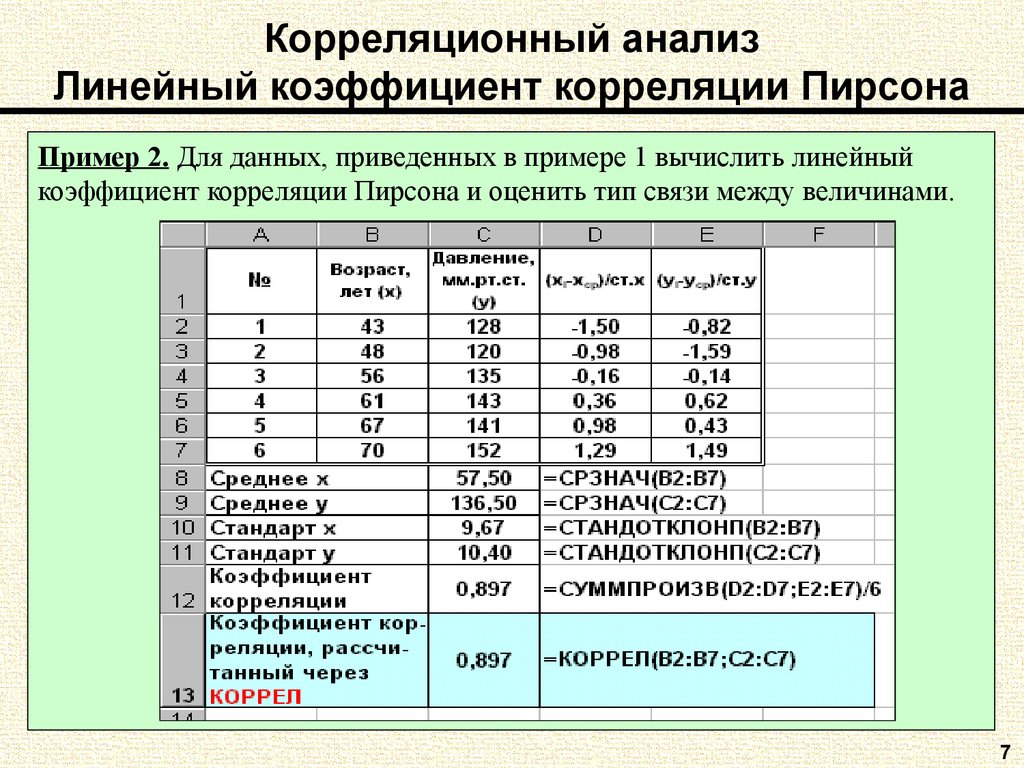
7. Корреляционный анализ Линейный коэффициент корреляции Пирсона
Пример 2. Для данных, приведенных в примере 1 вычислить линейныйкоэффициент корреляции Пирсона и оценить тип связи между величинами.
7
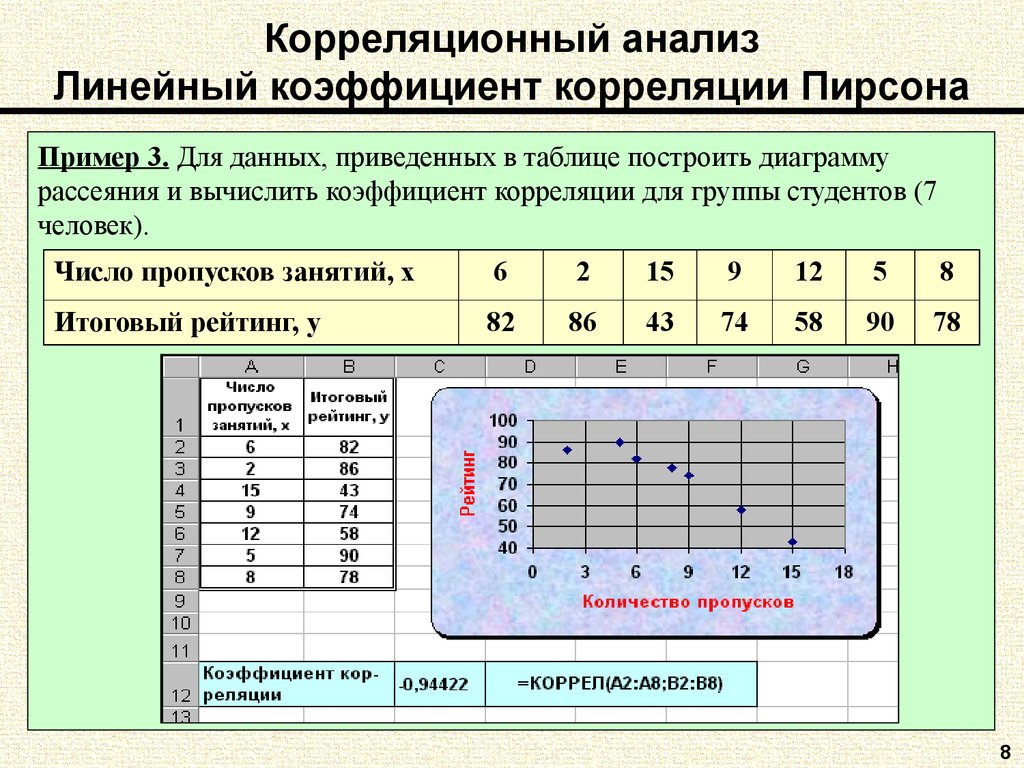
8. Корреляционный анализ Линейный коэффициент корреляции Пирсона
Пример 3. Для данных, приведенных в таблице построить диаграммурассеяния и вычислить коэффициент корреляции для группы студентов (7
человек).
Число пропусков занятий, x
6
2
15
9
12
5
8
Итоговый рейтинг, y
82
86
43
74
58
90
78
8
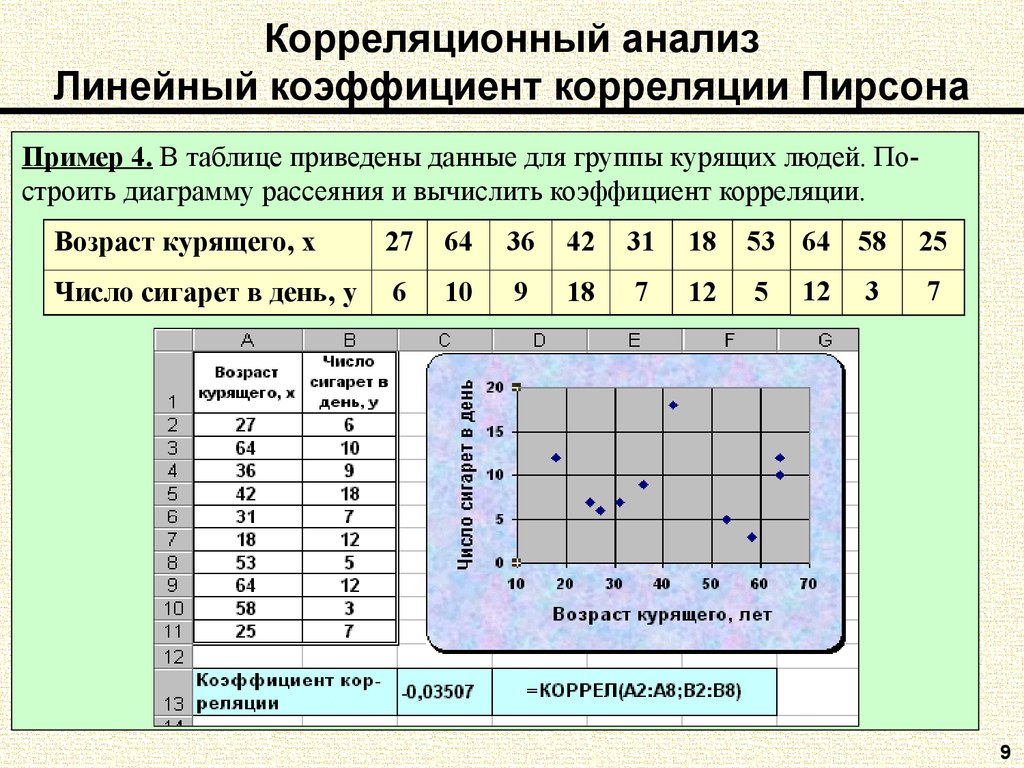
9. Корреляционный анализ Линейный коэффициент корреляции Пирсона
Пример 4. В таблице приведены данные для группы курящих людей. Построить диаграмму рассеяния и вычислить коэффициент корреляции.Возраст курящего, x
27
64
36
42
31
18
53 64 58
25
Число сигарет в день, y
6
10
9
18
7
12
5
12
7
3
9
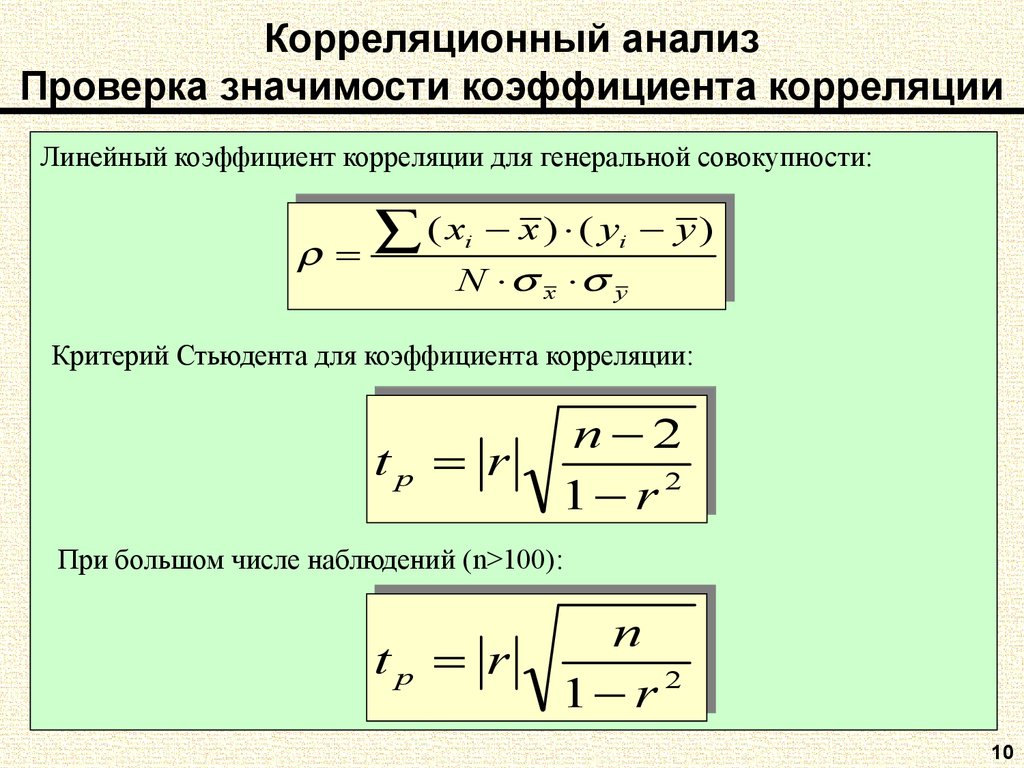
10. Корреляционный анализ Проверка значимости коэффициента корреляции
Линейный коэффициент корреляции для генеральной совокупности:(xx xx)) ((yy yy))
(
ii
ii
N
xx
yy
N
Критерий Стьюдента для коэффициента корреляции:
n
22
n
rr
ttpp
22
1
r
1 r
При большом числе наблюдений (n>100):
n
n
rr
ttpp
22
1
r
1 r
10
11. Корреляционный анализ Проверка значимости коэффициента корреляции
Оценка значимости коэффициента корреляции проводится с помощью аппарата проверки гипотез.Относительно генерального коэффициента корреляции можно выдвинуть
две гипотезы:
- генеральный коэффициент корреляции равен 0 (основная гипотеза);
- генеральный коэффициент корреляции отличен от 0.
Сформировав выборку и рассчитав её коэффициент корреляции r,
необходимо решить – является ли его значение настолько большим,
чтобы вероятность (по различным выборкам) выпадения такого значения при нулевом генеральном коэффициенте корреляции была
бы мала (меньше уровня значимости). Если является, то в этом случае основная гипотеза отвергается, а коэффициент корреляции и установленная зависимость между величинами полагаются значимыми.
11
12. Корреляционный анализ Проверка значимости коэффициента корреляции
Пример 5. Исследовать значимость коэффициента корреляции, рассчитанного в примере 2.1) Сформулируем проверяемые утверждения:
Н0: =0 (в генеральной совокупности нет зависимости, найденная
зависимость случайна);
Н1: 0 (найденная зависимость справедлива для генеральной
совокупности).
2) Находим критическое значение критерия Стьюдента:
при р=0,05 и k=6-1=5 tкр=2,571
3) Находим расчетное значение критерия Стьюдента:
tр=4,059
4) Находим критическую область значения критерия Стьюдента:
|tр| tкр
12
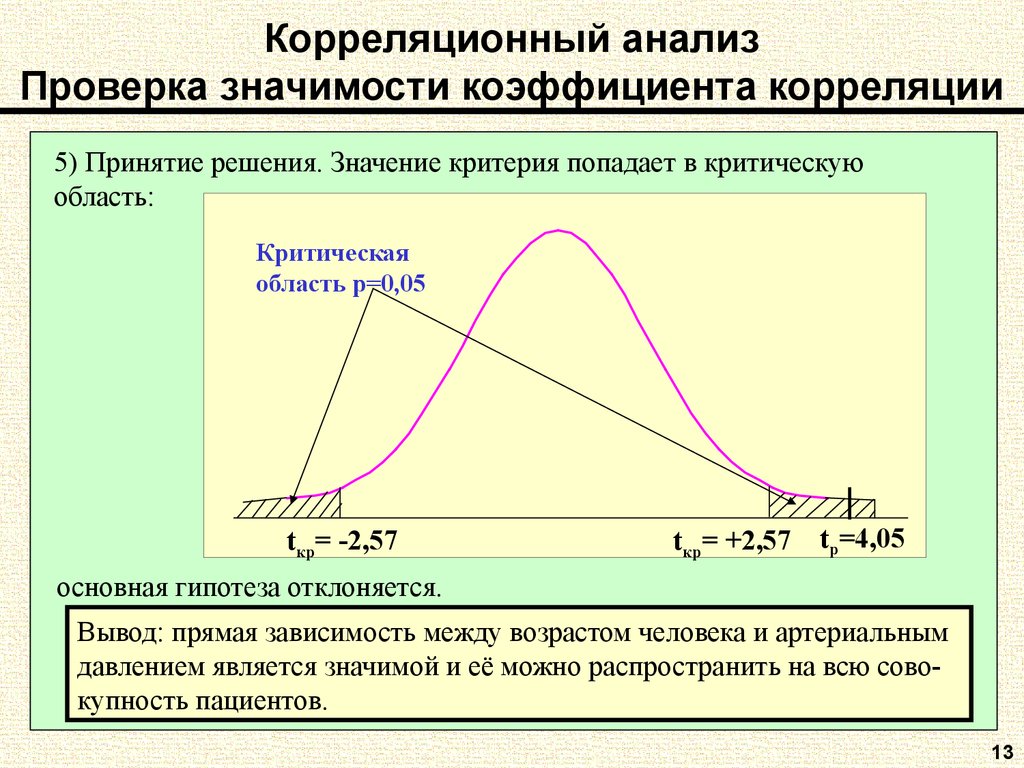
13. Корреляционный анализ Проверка значимости коэффициента корреляции
5) Принятие решения. Значение критерия попадает в критическуюобласть:
Критическая
область р=0,05
tкр= -2,57
tкр= +2,57
tр=4,05
основная гипотеза отклоняется.
Вывод: прямая зависимость между возрастом человека и артериальным
давлением является значимой и её можно распространить на всю совокупность пациентов.
13
14. Регрессионный анализ
Диаграммарассеяния
Проверка
значимости
коэффициента
корреляции
Построение
уравнения
регрессии
Наиболее распространенным способом построения уравнения регрессии
является метод наименьших квадратов (МНК).
Метод МНК для получения уравнения регрессии основан на минимизации
суммы квадратов остатков:
nn
22
min
min
SS
yyii ((aa00 ((aaii,,xxii))))
ii 11
Уравнение регрессии является линейным относительно коэффициентов aj (j=0,1,…,n).
14
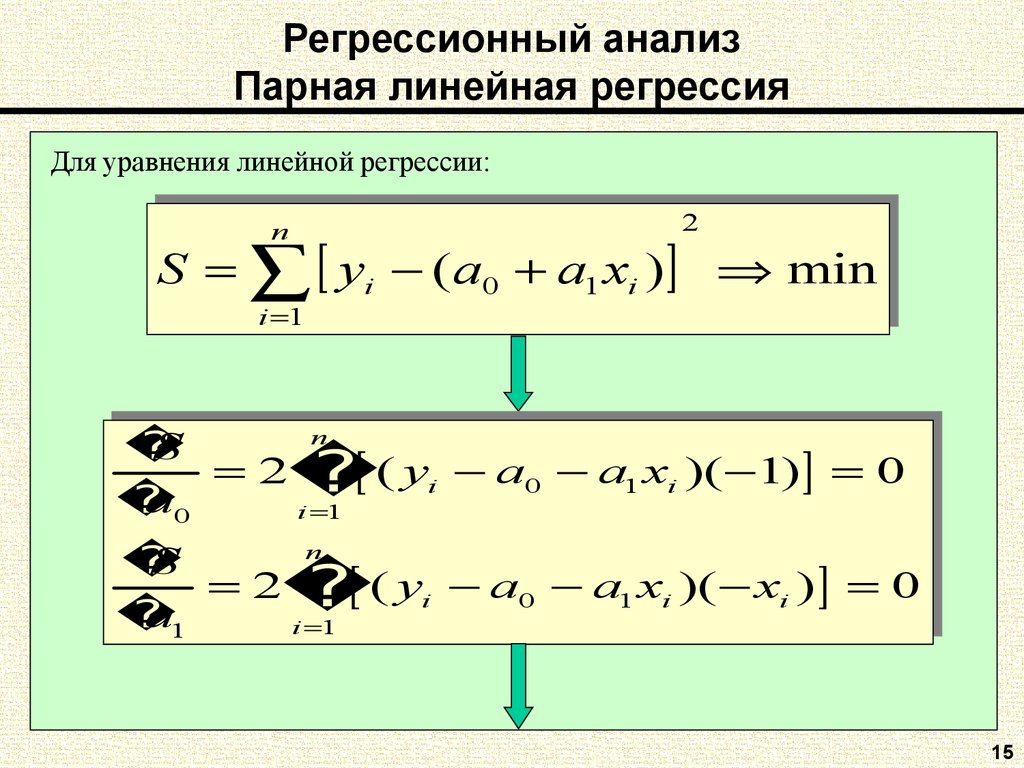
15. Регрессионный анализ Парная линейная регрессия
Для уравнения линейной регрессии:nn
22
min
min
SS
yyii ((aa00 аа11xxii))
ii 11
nn
S
S 2
)(
1)
1)
0
0
((yyii aa00 aa11xxii)(
2
a00
a
ii 11
nn
S
S 2
)(
xxii))
0
0
((yyii aa00 aa11xxii)(
2
a11
a
ii 11
15
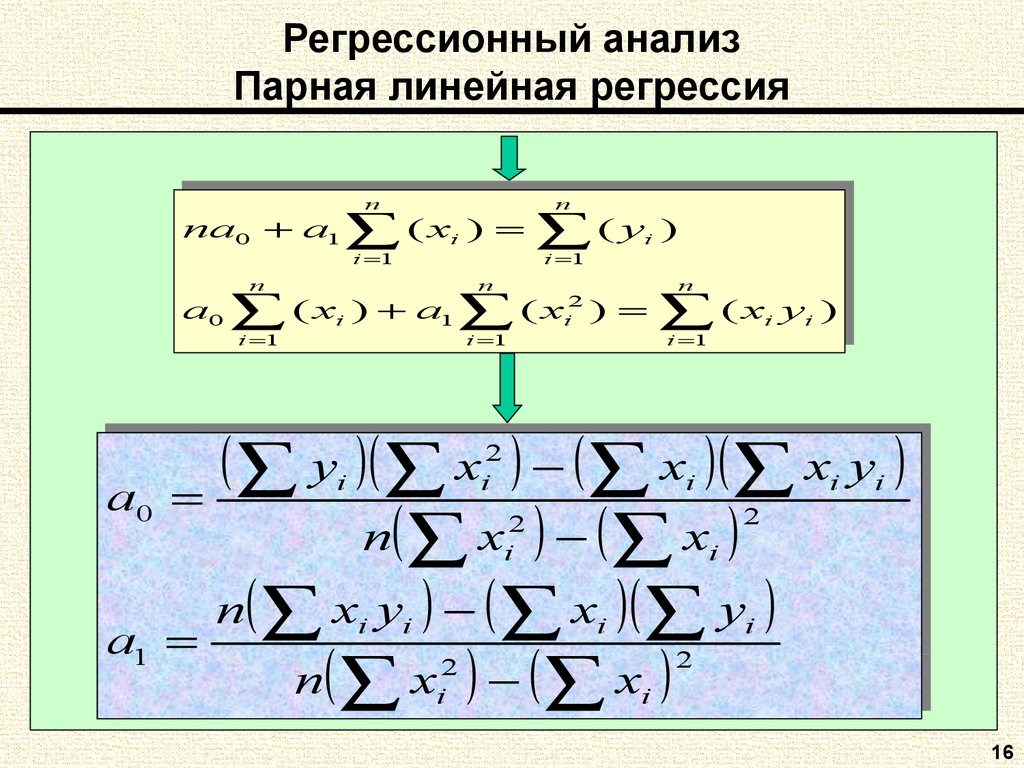
16. Регрессионный анализ Парная линейная регрессия
nn
n
n
i 1
i 1
i 1
i 1
na0
a
a1 ((x
xi))
((y
na
yii))
0
1
i
n
n
n
n
n
n
a0 ((x
xi))
a
a1 ((x
x ))
((x
a
xiiyyii))
0
i
1
i 1
i 1
aa00
aa11
i 1
i 1
2
2
i
i
i 1
i 1
y
x
x
x
y
y
x
x
x
y
nn
xx
xx
nn
xx yy
xx
yy
nn
xx
xx
22
ii
ii
ii
22
ii
ii
ii
ii
ii
ii
22
ii
22
ii
22
ii
ii
16
17. Регрессионный анализ Парная линейная регрессия
yd6
d7
d5
d3
d1
d2
d4
nn
dd
ii 11
ii
min
min
x
17
18. Регрессионный анализ Парная линейная регрессия
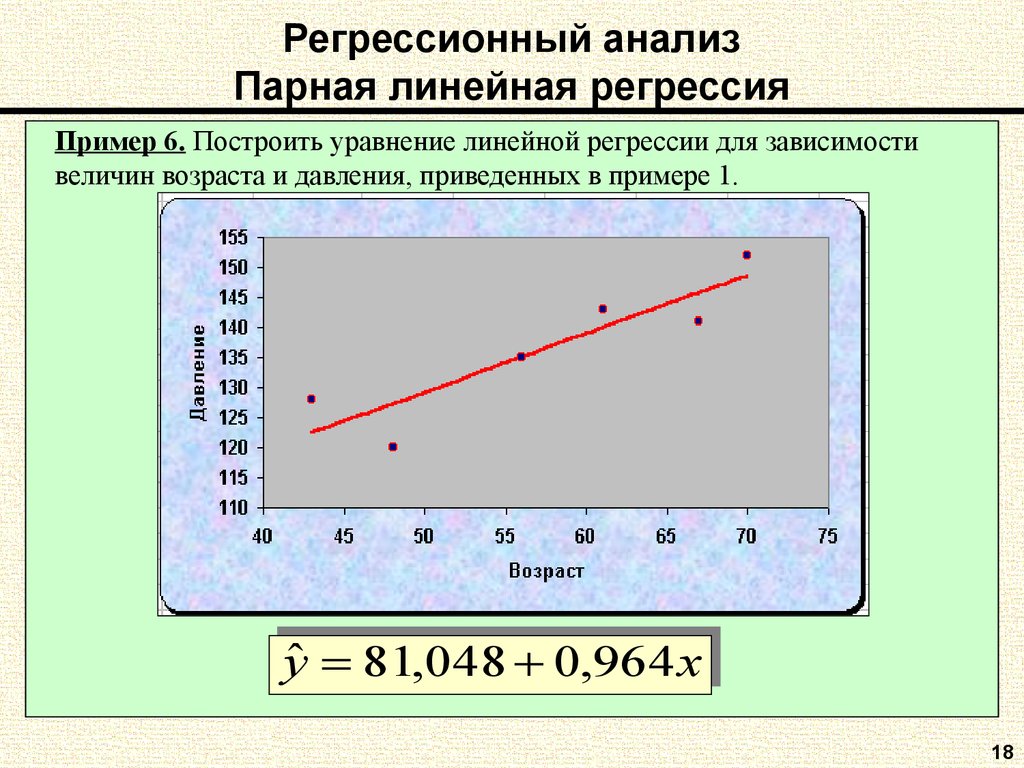
Пример 6. Построить уравнение линейной регрессии для зависимостивеличин возраста и давления, приведенных в примере 1.
81,,048
048 00,,964
964xx
yˆyˆ 81
18
19. Регрессионный анализ Парная линейная регрессия
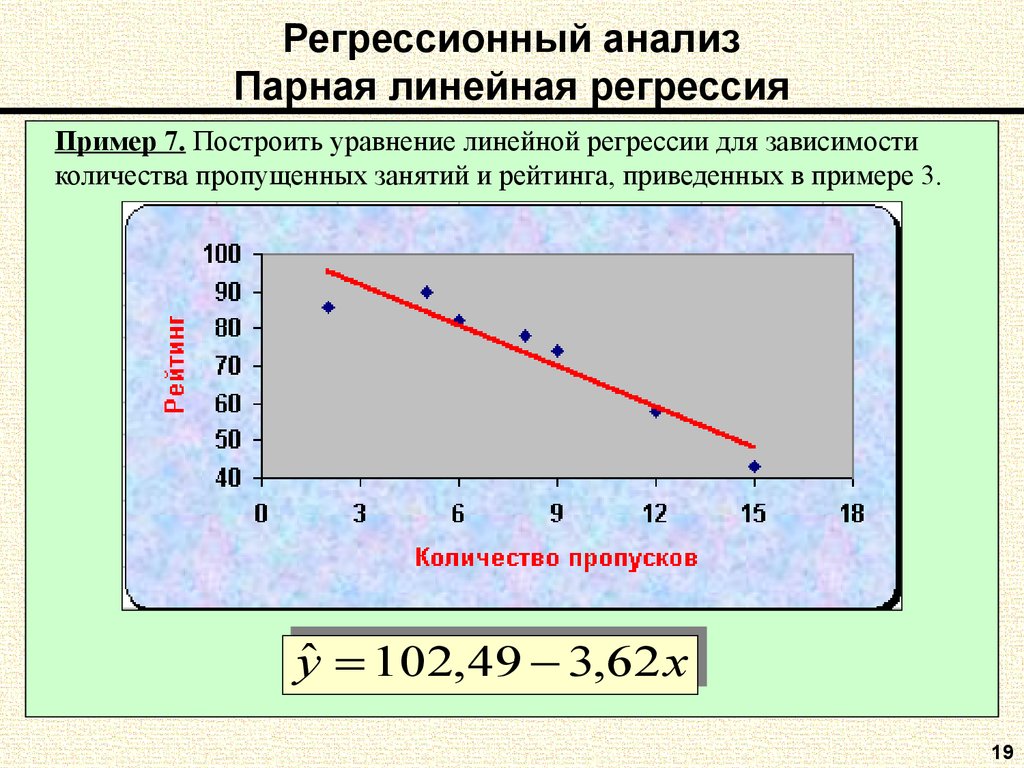
Пример 7. Построить уравнение линейной регрессии для зависимостиколичества пропущенных занятий и рейтинга, приведенных в примере 3.
102,,49
49 33,,62
62xx
yˆyˆ 102
19
20. Регрессионный анализ Парная линейная регрессия
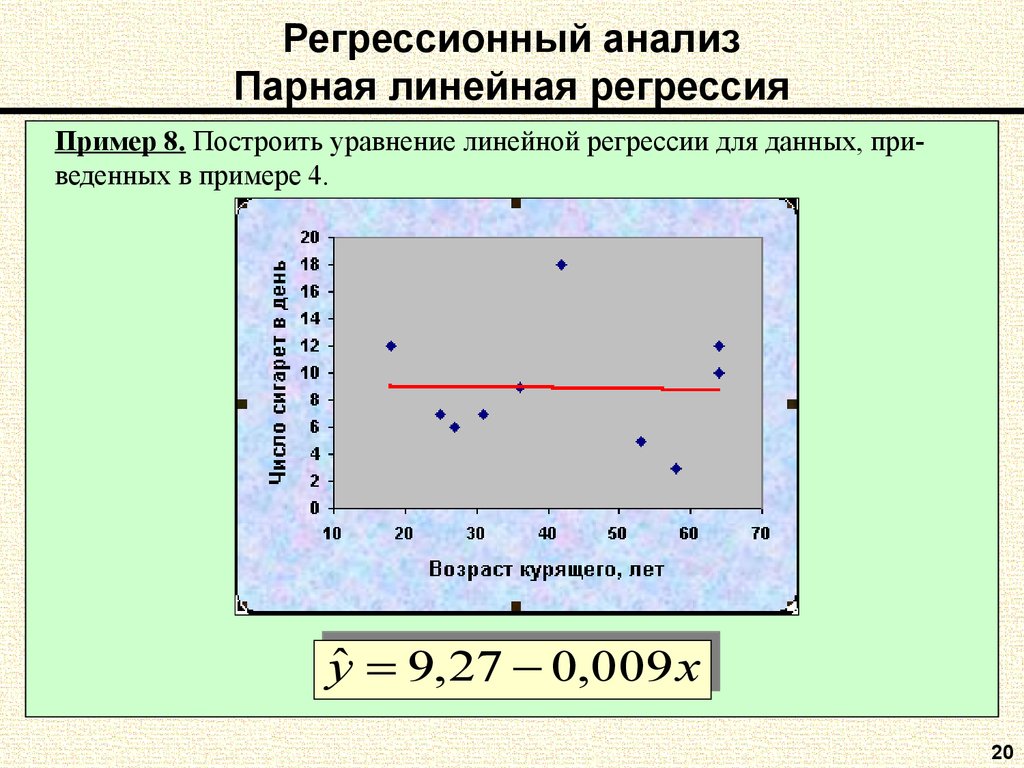
Пример 8. Построить уравнение линейной регрессии для данных, приведенных в примере 4.27 00,,009
009xx
yˆyˆ 99,,27
20
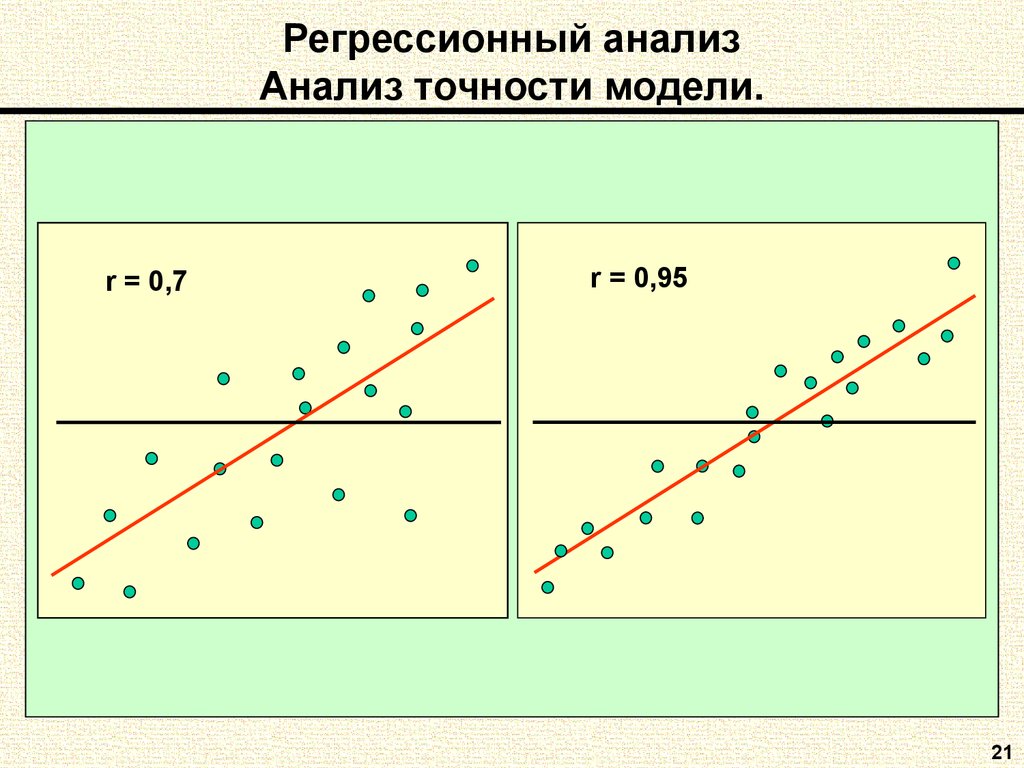
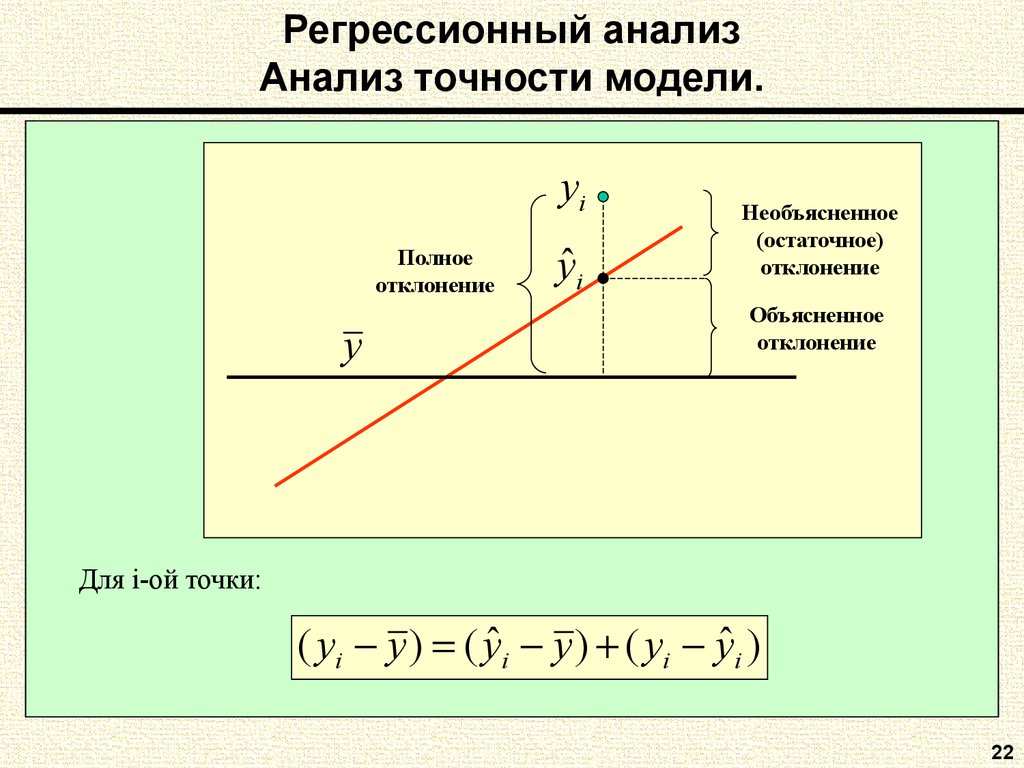
21. Регрессионный анализ Анализ точности модели.
r = 0,7r = 0,95
21
22. Регрессионный анализ Анализ точности модели.
yiПолное
отклонение
y
yˆ i
Необъясненное
(остаточное)
отклонение
Объясненное
отклонение
Для i-ой точки:
( yi y ) ( yˆ i y ) ( yi yˆ i )
22
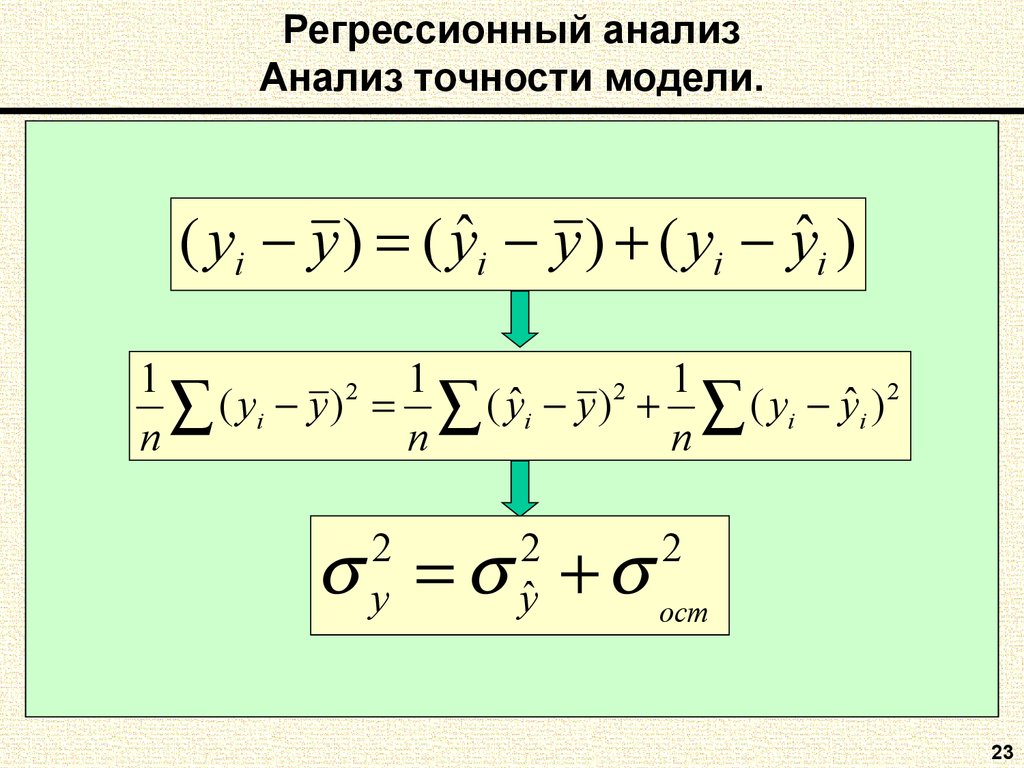
23. Регрессионный анализ Анализ точности модели.
( yi y ) ( yˆ i y ) ( yi yˆ i )1
1
1
2
2
2
ˆ
ˆ
(
y
y
)
(
y
y
)
(
y
y
)
i
i
i
i
n
n
n
ocm
2
y
2
yˆ
2
23
24. Регрессионный анализ Анализ точности модели.
Коэффициент детерминации:2
2
r
r
2
2
S yˆ
S
ˆ
y
2
2
Syy
S
Коэффициент детерминации является основной характеристикой
регрессионной модели и показывает, какую долю вариации (изменчивости) результативного признака можно объяснить изменением
факторного признака.
Одним из практических применений коэффициента детерминации
является оценка качества и сравнение между собой различных моделей (линейной и нелинейных) парной регрессии.
24
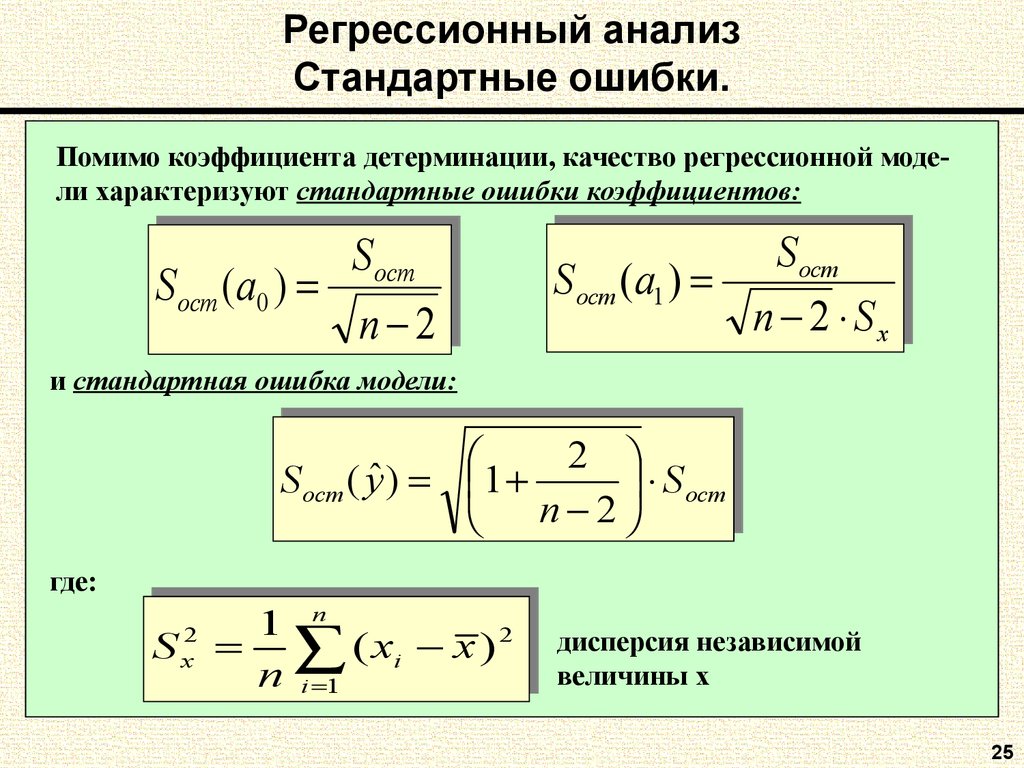
25. Регрессионный анализ Стандартные ошибки.
Помимо коэффициента детерминации, качество регрессионной модели характеризуют стандартные ошибки коэффициентов:Socm
S
ocm
SSocm
ocm((aa00))
nn 22
Socm
S
ocm
S
(
a
)
S ocm
ocm( a11)
nn 22 SSxx
и стандартная ошибка модели:
2
2
SSocm
ˆyˆ)) 11
SSocm
ocm((y
ocm
nn 22
где:
nn
1
22 1
22
S
(
x
x
)
S xx
( xii x )
nn ii 11
дисперсия независимой
величины х
25
26. Регрессионный анализ Схема проверки гипотез о значимости коэффициентов.
Пример 9. На основании данных наблюдений в США за 25 – летнийпериод (1959 – 1983 годы) построена зависимость суммарных расходов
на питание (y) от располагаемых доходов (х):
ˆ 55,3 0,093 x
y
S ocm ( a0 ) 2,4; S ocm ( a1 ) 0,003
При уровне значимости 5% проверить гипотезы о значимости
коэффициентов.
26
27.
Регрессионный анализСхема проверки гипотез о значимости
коэффициентов.
1) Гипотезы для обоих коэффициентов формулируются одинаково:
Н0: a0=0; H1: a0 0.
Н0: a1=0; H1: a1 0.
2) Находим критическое значение критерия Стьюдента:
при р=0,05 и k=25-2=23, tкр=2,069
3) Находим расчетные значения критерия Стьюдента:
tр(a0)= a0/Socm(a0)=55,3/2,4=23,04
tр(a1)= a1/Socm(a1)=0,093/0,003=31
4) Принятие решения. Основные гипотезы отклоняются, коэффициенты
значимы.
a -S (a )*t <a <a +S (a )* t
0
ocm
0
kp
0
0
ocm
0
kp
a1-Socm(a1)*tkp<a1<a1+Socm(a1)* tkp
27
28.
Регрессионный анализПроверка гипотезы о значимости модели.
Для решения вопроса действительно ли полученное при оценке регрессии значение r2 отражает истинную зависимость или оно получено случайно, применяется процедура проверки гипотез, основанная на анализе F-критерия (критерия Фишера):
22
22
22
S
S
S
S yy
S ост
S большая
ост
большая
F
или
F
Fрр 22 или Fрр
22
22
S
S
Sост
S yy
SSменьшая
ост
меньшая
nn
22
S
S ост
ост
ˆi
y
ˆ
y
i yyii
i i 11
nn
22
m
m
nn
22
;
S
; S yy
2
%
y
y
%
y
y
i
i
i i 11
2
11
nn
где m – число параметров уравнения регрессии ( включая свободный ):
28
29.
Регрессионный анализПроверка гипотезы о значимости модели.
Способы нахождения критерия Фишера.
1) С помощью таблиц распределения (k1 – число степеней свободы
числителя, k2 – число степеней свободы знаменателя):
Уровень значимости р=0,05
k2
k1
1
2
…
6
…
24
…
1
161
200
…
234
…
249
…
2
18,51
19,00
…
19,33
…
19,45
…
…
…
…
…
…
…
…
…
23
4,28
3,42
…
2,53
…
2,00
…
…
…
…
…
…
…
…
…
29
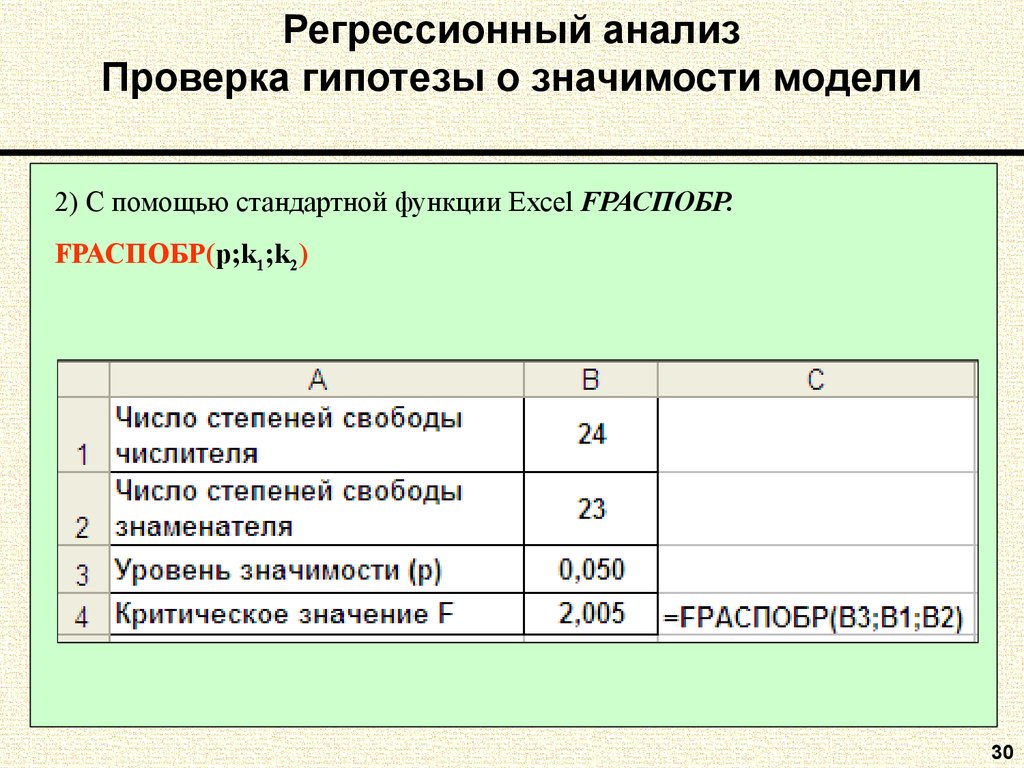
30. Регрессионный анализ Проверка гипотезы о значимости модели
2) С помощью стандартной функции Excel FРАСПОБР.FРАСПОБР(p;k1;k2)
30
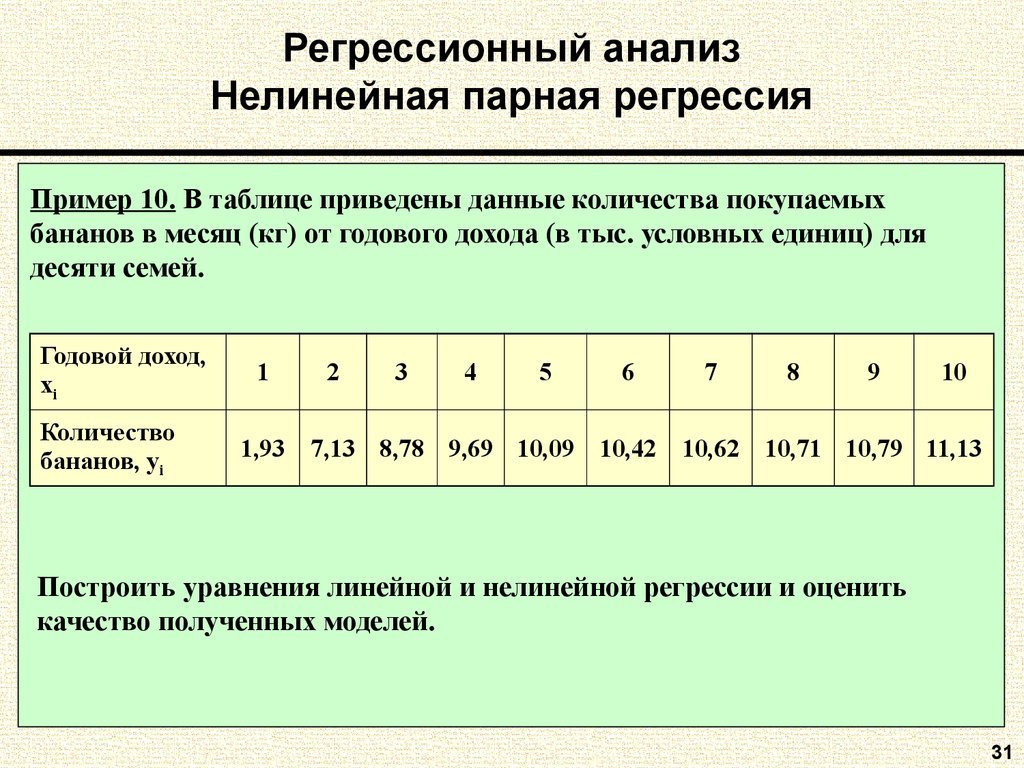
31. Регрессионный анализ Нелинейная парная регрессия
Пример 10. В таблице приведены данные количества покупаемыхбананов в месяц (кг) от годового дохода (в тыс. условных единиц) для
десяти семей.
Годовой доход,
xi
Количество
бананов, yi
1
2
3
4
5
6
7
8
9
10
1,93 7,13 8,78 9,69 10,09 10,42 10,62 10,71 10,79 11,13
Построить уравнения линейной и нелинейной регрессии и оценить
качество полученных моделей.
31
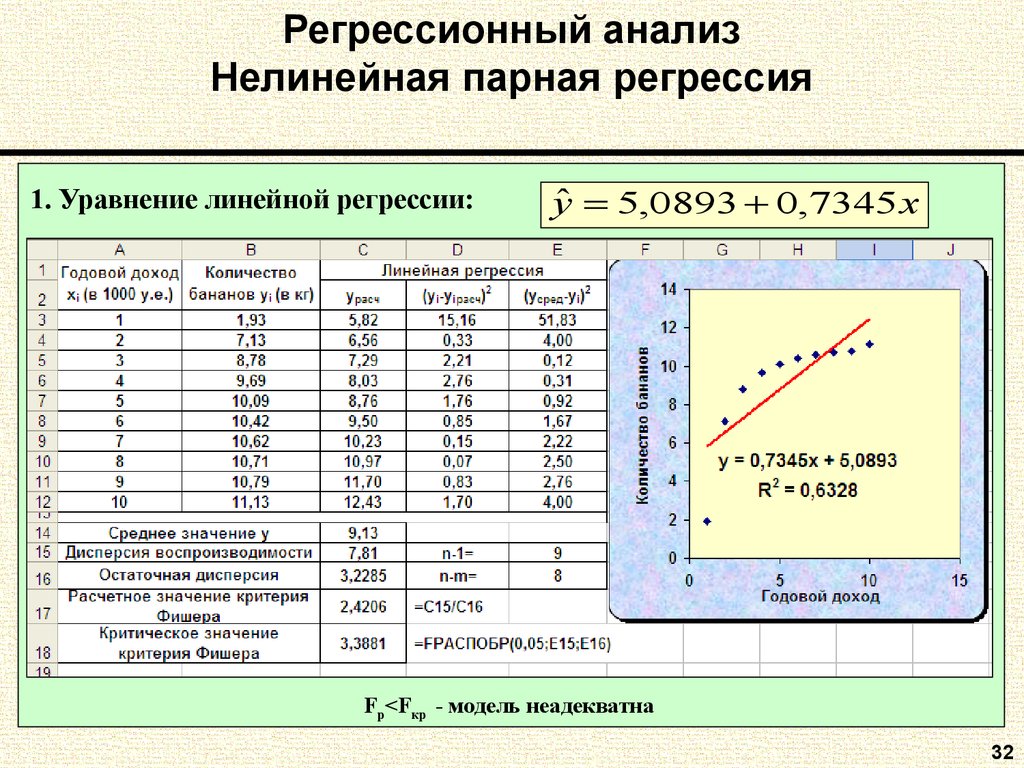
32. Регрессионный анализ Нелинейная парная регрессия
1. Уравнение линейной регрессии:yˆ 5,0893 0,7345 x
Fp<Fкр - модель неадекватна
32
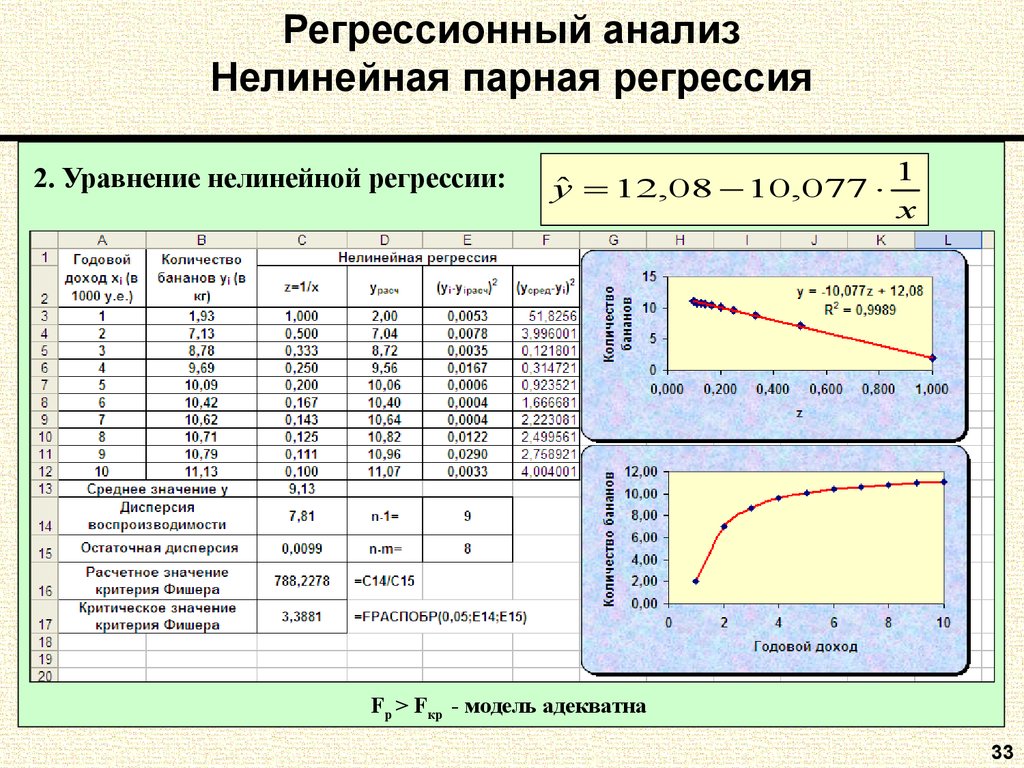
33. Регрессионный анализ Нелинейная парная регрессия
2. Уравнение нелинейной регрессии:ˆ 12,08 10,077
y
1
x
Fp > Fкр - модель адекватна
33
34. Регрессионный анализ Нелинейная парная регрессия
Нелинейные модели парной регрессии и преобразование переменных.Связь
Преобразования
Линейное
уравнение
y=exp(a0+a1x)
ln(y)=u
u=a0+a1x
Обратная по y
y=1/(a0+a1x)
1/y=u
u=a0+a1x
Обратная по x
y=a0+a1/x
1/x=z
y=a0+a1z
Дважды обратная
y=1/(a0+a1/ x)
1/x=z; 1/y=u
u=a0+a1z
Логарифм по x
y=a0+a1ln(x)
y=a x a1
ln(x)=z
y=a0+a1z
ln(x)=z; ln(y)=u; ln(a0)=b
u=b+a1x
Квадратный корень по x
y=a0+a1x1/2
x1/2=z
y=a0+a1z
Квадратный корень по y
y=(a0+a1x)1/2
y2=u
u=a0+a1x
y=exp(a0+a1/x)
ln(y)=u; 1/x=z
u=a0+a1z
Тип модели
Экспоненциальная
Мультипликативная
S-кривая
0
34











 mathematics
mathematics








