Статистическое изучение взаимосвязей. Корреляционный и регрессионный анализ

1. СТАТИСТИЧЕСКОЕ ИЗУЧЕНИЕ ВЗАИМОСВЯЗЕЙ

корреляционный и регрессионный
анализ

2. Производственная функция

−
экономико-статистическая модель связи,
характеризующая изменение уровня
результативных производственных
показателей в зависимости от одного или
ряда важнейших производственных
факторов

3. Способы построения производственных функций

−
−
−
аналитический – построение математического
уравнения, моделирующего зависимость
результативного экономического показателя от
одного или ряда производственных факторов
табличный - представление результативного
показателя, соответствующего определенным
значениям факторов, в виде таблицы
графический - представление зависимости
исследуемого показателя от фактора в виде
графика

4. Классификация производственных функций

по степени влияния человека на исследуемый
результативный показатель
по признаку сложности
объективные
субъективные
объективно-субъективные
простые - немногофакторные, элементарные зависимости
сложные - зависимости от целого ряда факторов
по степени полноты учета факторных признаков
закрытые - простые детерминированные зависимости
открытые - сложные стохастические производственные
функции

5. Классификация производственных функций

по числу факторов, учтенных в модели
по виду математической модели
однофакторные
Многофакторные
линейные
криволинейные
по направлению влияния факторных признаков
на зависимый показатель
прямые
обратные
комбинированные

6. Классификация производственных функций

по виду ряда данных
по полноте учета информации
Выборочные
Генеральные
по временному фактору
Вариационные
Динамические
Вариационно-динамические
Однопериодные
Многопериодные
по уровню управления
Межотраслевые
Отраслевые
Региональные
Межхозяйственные
Хозяйственные

7. Виды производственных функций

Определяется видом уравнения, которое используется в
качестве ее математической модели
Одно и то же математическое уравнение как
математическая модель может использоваться для
построения нескольких (различных) зависимостей.
Одна и та же производственная связь может
имитироваться разными математическими уравнениями.
Апробированные математические модели с изменением
места и времени часто оказываются практически
неприемлемыми.
Идеальной производственной функцией следует считать
ту, которая наиболее точно воспроизводит исследуемое
явление или процесс. Но построение таких идеальных
статистико-экономических моделей возможно только в
простейших случаях.

8. Виды производственных функций

однофакторная статистико-экономическая
зависимость - линейная функция - прямая
пропорциональная зависимость. Ее графиком
является прямая, которая проходит через начало
координат. Число (а) называется угловым
коэффициентом прямой. С помощью этой
производственной функции моделируют
зависимость, например, стоимости продукции (у)
от ее количества или цены ее единицы
y ax

9. Виды производственных функций

Линейная производственная функция
моделирует зависимость, например,
уровня оплаты труда (у) от его
производительности (х).
y a 0 a1 x

10. Виды производственных функций

Парабола второго порядка - производственная функция,
которую целесообразно использовать для моделирования
зависимостей, имеющих одну экстремальную точку
(минимума или максимума). Такой является, например,
зависимость урожая культуры (у) от внесения удобрений.
y a0 a1 x a2 x
2

11. Виды производственных функций

Целая рациональная функция, которую используют
тогда, когда исследуемая зависимость содержит ряд
экстремумов.
y a0 a1 x a2 x ... an x
2
n
Гипербола, сдвинутая по оси ординат на а0 – которую
используют для моделирования обратных
пропорциональных зависимостей, например, издержек на
единицу продукции (у) от производительности
оборудования (х).
a1
y a0
x

12. Виды производственных функций

a1 a2
y a0 2
x x
a1 a2
an
y a0 2 ... n
x x
x

13. Виды производственных функций

степенная функция
y a0 x
a1
показательная производственная функция – для анализа
рядов динамики и уровня важнейших экономических
параметров предприятия
y a0a1
x

14. Виды производственных функций

Для моделирования периодических, сезонных колебаний,
волнообразных процессов применяют различные
тригонометрические уравнения. Простейшими из них
являются уравнения синусоиды.
y sin x
y a sin x
y a0 a1 sin x

15. Виды производственных функций

многофакторная линейная функция
y a0 a1 x a2 x ... an x
обратная многофакторной функции
a1 a2
an
y a0 2 ... n
x x
x

16. Виды производственных функций

многофакторная парабола второго порядка
y a0 a1 x1 a x a3 x2 a x a5 x1 x2
2
2 1
2
4 2

17. Направления использования производственных функций:

Определение влияния различных факторов на анализируемые
результативные показатели.
2. Поиск оптимального сочетания факторов, при котором
зависимый показатель достигает экстремального
(максимального или минимального) уровня.
3. Анализ, хозяйственных процессов предприятий, их подразделений
и объединений, происходящие под воздействием как
объективных, так и субъективных факторов, и результатов их
деятельности, характеризующихся определенной системой
показателей.
4. Прогнозирование и планирование уровня важнейших показателей
производства.
1.

18. Направления использования производственных функций:

5. Обработка информации. Экономической информацией
называют информацию об общественных процессах
производства, распределения, обмена и потребления
материальных благ.
6. Обоснование нормативов.
7. Обоснование уровня оплаты труда.

19. Классификация взаимосвязей

теснота связи
характер связи
прямые
обратные
вид уравнения
функциональные (полные)
корреляционные (неполные)
линейные (прямолинейные )
нелинейные (криволинейные )
количество факторов
однофакторные (парная зависимость)
многофакторные (множественная зависимость)

20. Задачи корреляционного анализа

измерение тесноты связи между
варьирующими признаками,
определение неизвестных причинных
связей,
оценка факторов оказывающих
наибольшее влияние на результативный
признак.

21. Задачи регрессионного анализа

установление формы зависимости,
определение функции регрессии,
использование уравнения для оценки
неизвестных значений зависимой
переменной.

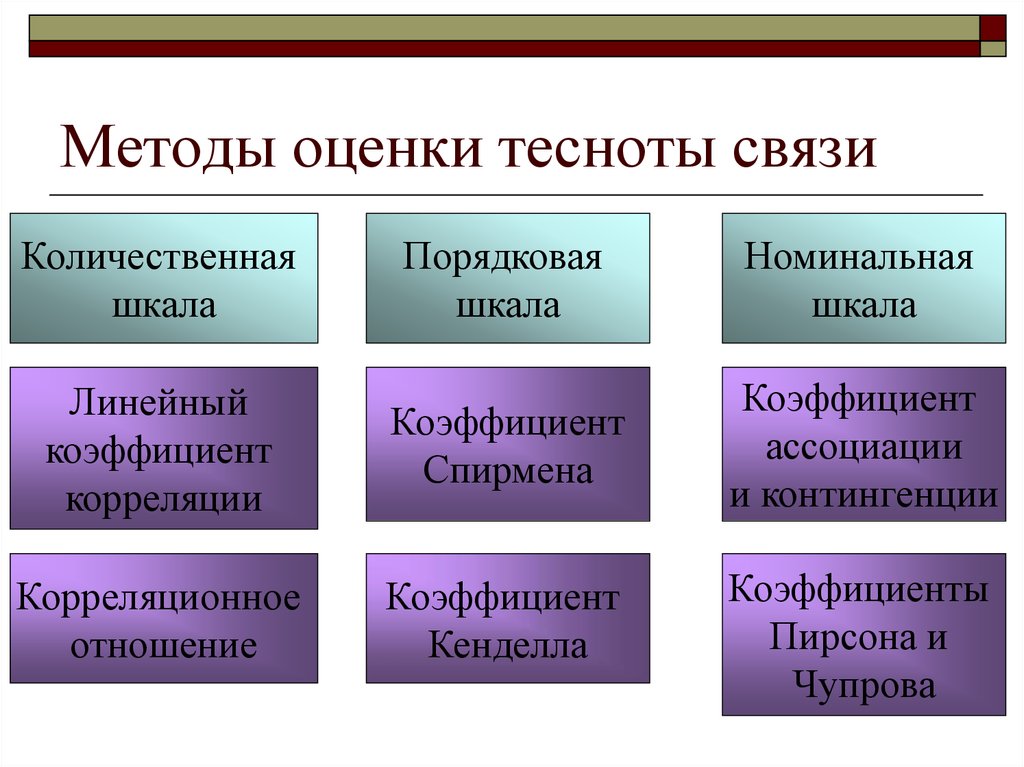
22. Методы оценки тесноты связи

Количественная
шкала
Порядковая
шкала
Номинальная
шкала
Линейный
коэффициент
корреляции
Коэффициент
Спирмена
Коэффициент
ассоциации
и контингенции
Корреляционное
отношение
Коэффициент
Кенделла
Коэффициенты
Пирсона и
Чупрова

23. Виды шкал

Количественная – используется для
описания количественных показателей;
Номинальная – шкала наименований
(атрибутивных и альтернативных
признаков) – (= и ≠);
Порядковая – применяется для измерения
упорядоченности объектов по одному или
нескольким признакам – (>, <, =).

24. Линейный коэффициент корреляции

rxy
n x y x y
n x x n y
2
2
2
y
2

25. Линейный коэффициент корреляции

r
x x y y
x x y y
2
2

26. Линейный коэффициент корреляции

r
xy x y
x y

27. Линейный коэффициент корреляции

Величина коэффициента
Характер связи
корреляции
До | ± 0,3 |
Практически отсутствует
| ± 0,3 | - | ± 0,5 |
Слабая
| ± 0,5 | - | ± 0,7 |
Умеренная
| ± 0,7 | - | ± 1,0 |
Сильная

28. Корреляционное отношение

2
yx
2
y
2
yx
2
y
Характеризует вариацию результативного
признака под влиянием факторного
Характеризует вариацию результативного
признака под влиянием всех факторов

29. Ранговый коэффициент корреляции Спирмена

1
6
n(n 1)
2
n
Ak Bk
2
k 1
Ak ранг _ k того _ наблюдения _ по _ показателю _ x;
Bk ранг _ k того _ наблюдения _ по _ показателю _ y;
n число _ пар _ наблюдений.

30. Ранговый коэффициент корреляции Кенделла

2S
n(n 1)
S – сумма баллов, если баллом +1 оценивается пара рангов,
имеющих по обоим показателям одинаковый порядок, а
баллом -1 – пара с разным порядком.

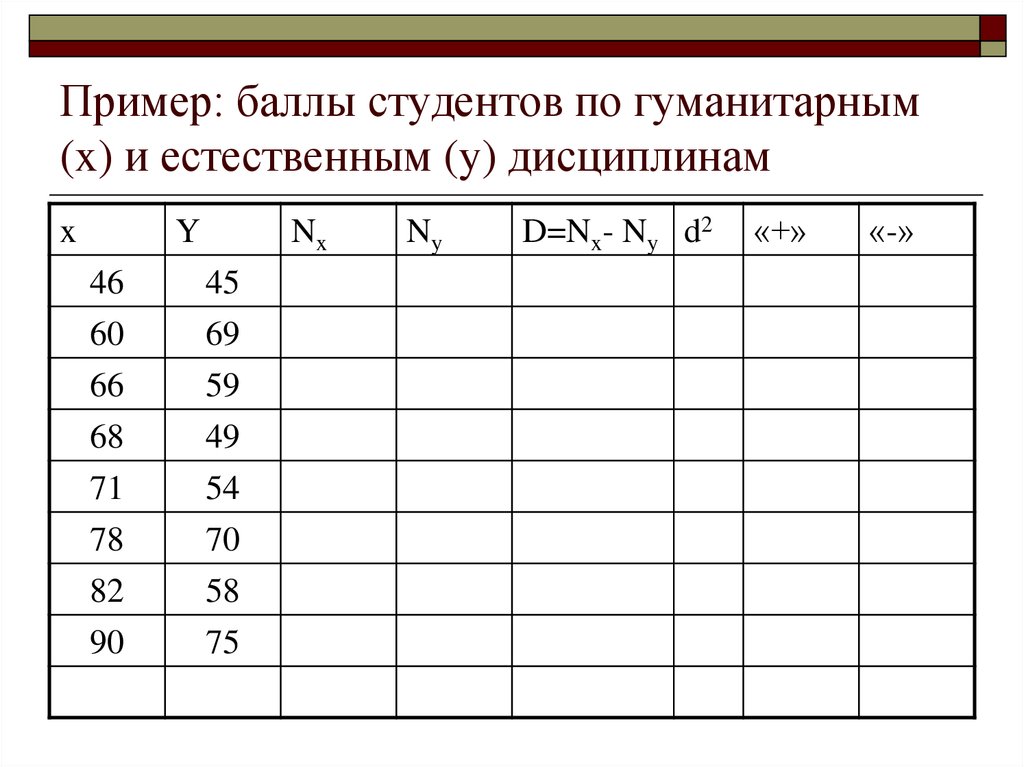
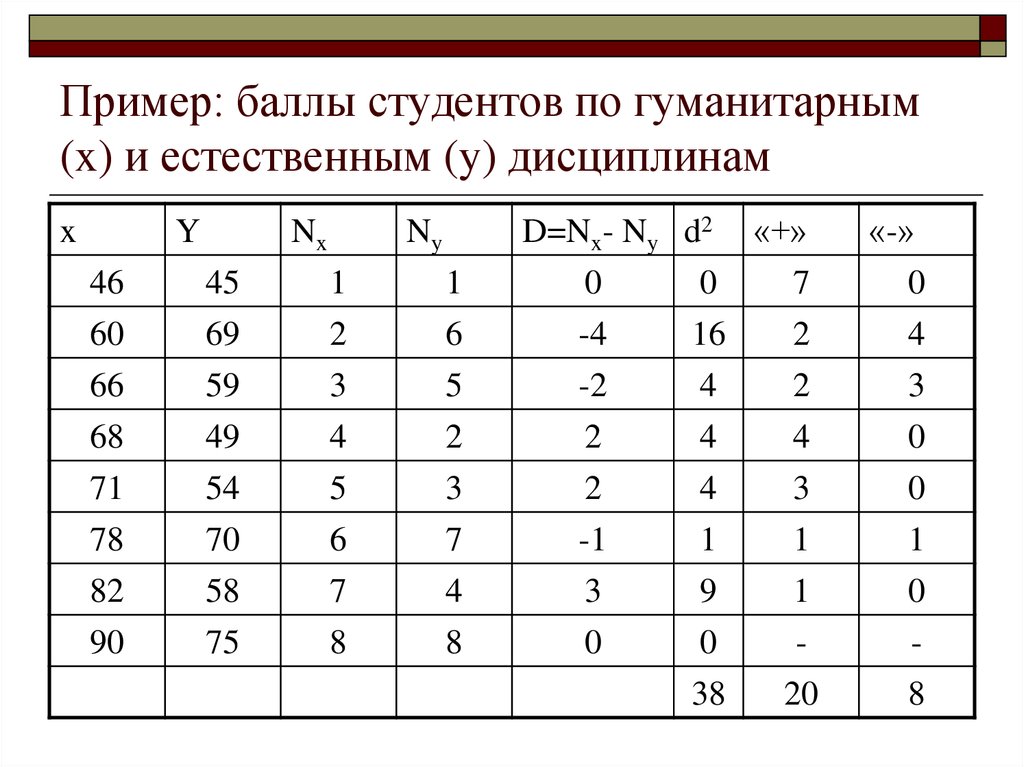
31. Пример: баллы студентов по гуманитарным (x) и естественным (y) дисциплинам

x
Y
Nx
46
60
45
69
66
59
68
71
49
54
78
82
90
70
58
75
Ny
D=Nx- Ny d2
«+»
«-»

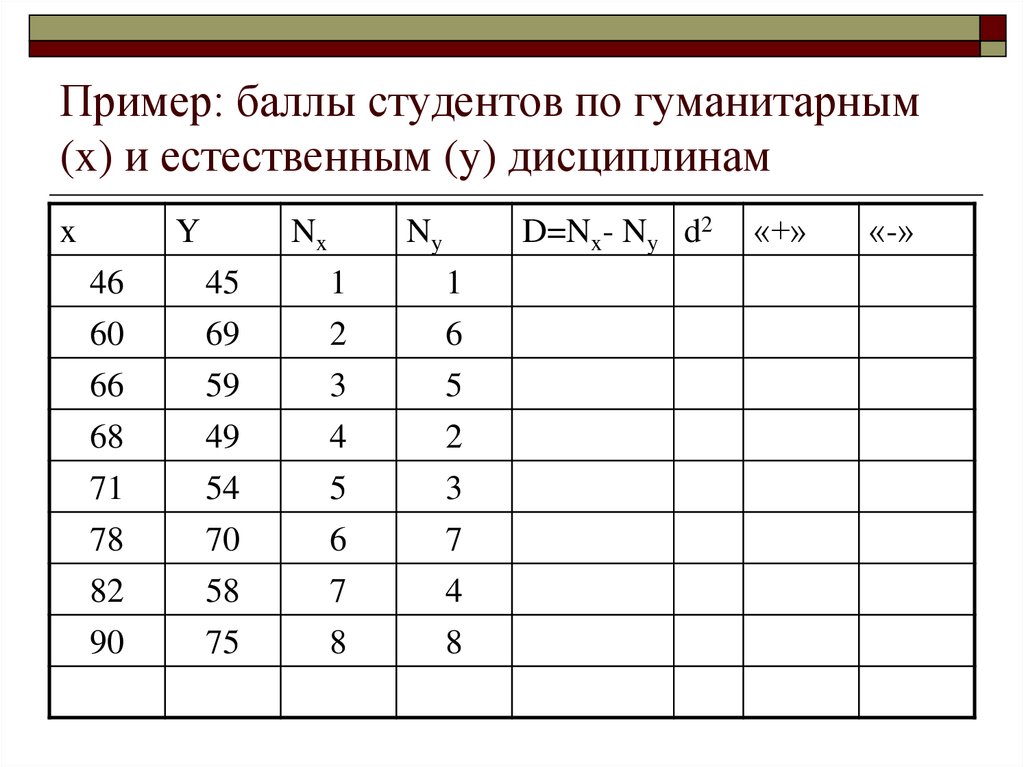
32. Пример: баллы студентов по гуманитарным (x) и естественным (y) дисциплинам

x
Y
Nx
D=Nx- Ny d2
Ny
46
60
45
69
1
2
1
6
66
59
3
5
68
71
49
54
4
5
2
3
78
82
90
70
58
75
6
7
8
7
4
8
«+»
«-»

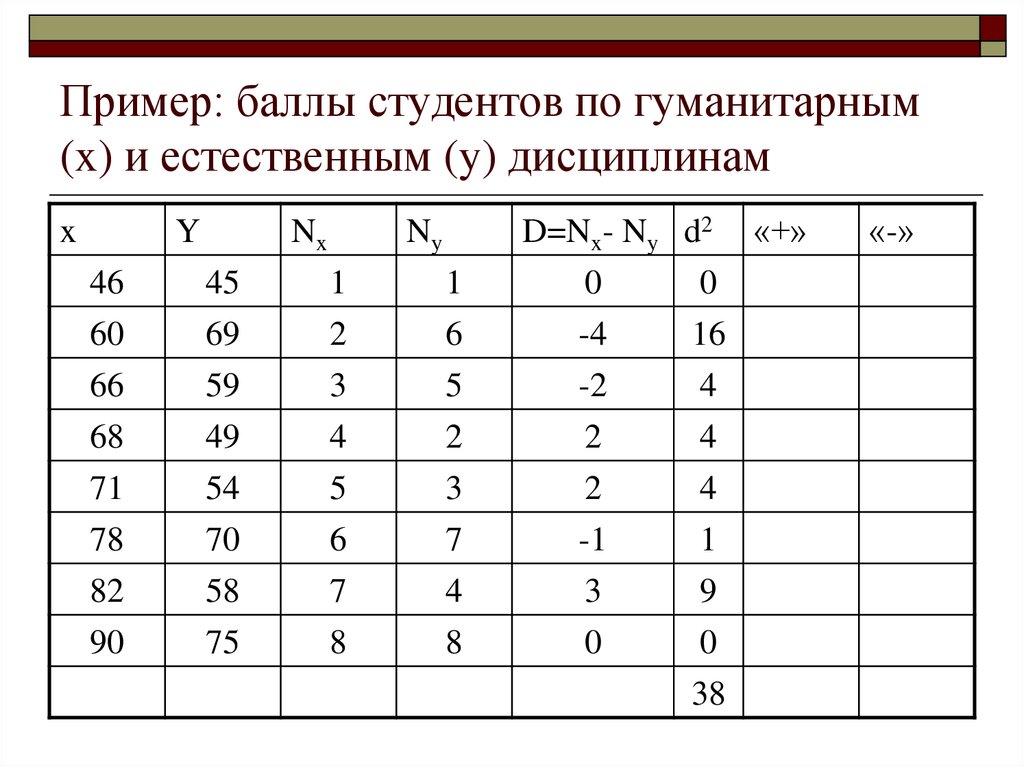
33. Пример: баллы студентов по гуманитарным (x) и естественным (y) дисциплинам

x
Y
Nx
Ny
D=Nx- Ny d2 «+»
0
0
-4
16
46
60
45
69
1
2
1
6
66
59
3
5
-2
4
68
71
49
54
4
5
2
3
2
2
4
4
78
82
90
70
58
75
6
7
8
7
4
8
-1
3
0
1
9
0
38
«-»

34. Пример: баллы студентов по гуманитарным (x) и естественным (y) дисциплинам

x
Y
Nx
Ny
D=Nx- Ny d2 «+»
0
0
7
-4
16
2
«-»
0
4
46
60
45
69
1
2
1
6
66
59
3
5
-2
4
2
3
68
71
49
54
4
5
2
3
2
2
4
4
4
3
0
0
78
82
90
70
58
75
6
7
8
7
4
8
-1
3
0
1
9
0
1
1
-
1
0
-
38
20
8

35. Ранговый коэффициент корреляции Спирмена

6 * 38
1
1 0.453 0.547
8(64 1)

36. Ранговый коэффициент корреляции Кенделла

2(20 8) 24
0.429
8(8 1)
56

37. Номинальные шкалы

X
Y
1
2
1
a
b
a+b
2
c
d
c+d
a+c
b+d

38. Коэффициент ассоциации

a d b c
ka
a d b c
Если ka > 0,5, то между признаками имеется существенная
взаимосвязь

39. Коэффициент контингенции

a d b c
kk
a b c d a c b d
Если kk ≥ 0,3, то между признаками имеется существенная
взаимосвязь

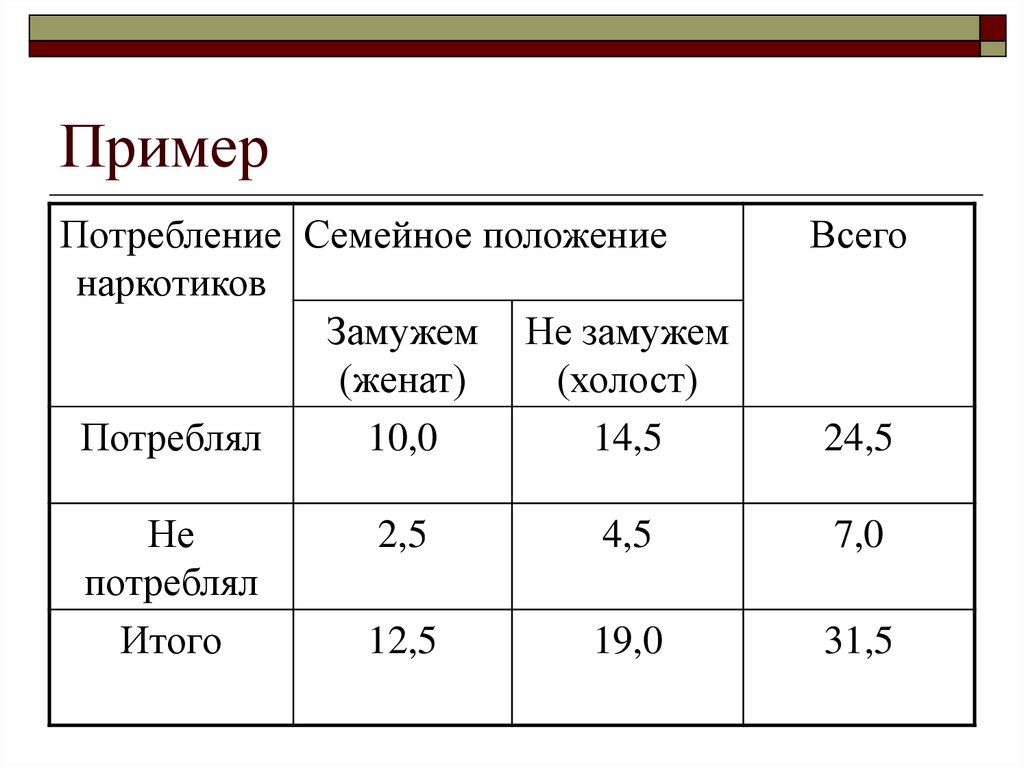
40. Пример

Потребление Семейное положение
наркотиков
Замужем Не замужем
(женат)
(холост)
Потреблял
10,0
14,5
Не
потреблял
Итого
Всего
24,5
2,5
4,5
7,0
12,5
19,0
31,5

41. Пример

10 * 4.5 14.5 * 2.5
Ka
0.108
10 * 4.5 14.5 * 2.5
10 * 4.5 14.5 * 2.5
Kk
10 4.5 * 14.5 4.5 * 4.5 2.5 * 2.5 10
0.043

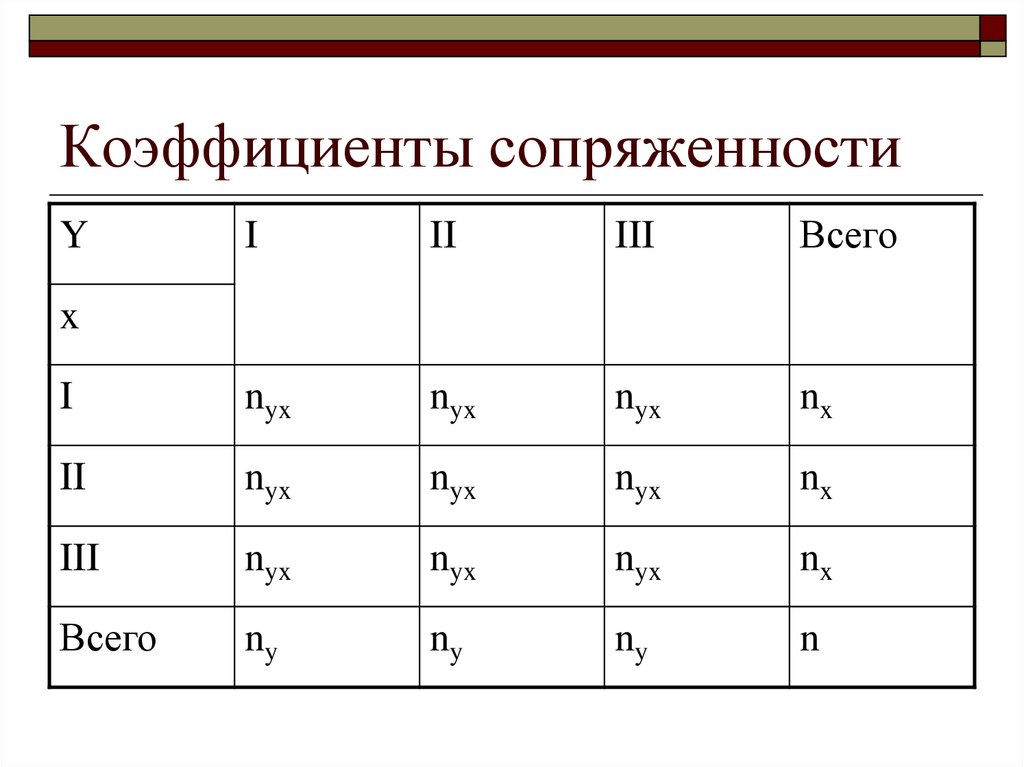
42. Коэффициенты сопряженности

I
II
III
Всего
I
nyx
nyx
nyx
nx
II
nyx
nyx
nyx
nx
III
nyx
nyx
nyx
nx
Всего
ny
ny
ny
n
Y
x

43. Коэффициент сопряженности Пирсона

KП
2
1
2
2
n
2
xy
nx n y
где
n
1
1 2
n
ny
nxy2
2
xy
x
n
nx
y

44. Коэффициент сопряженности Чупрова

KЧ
2
m1 1 m2 1
m1 – количество градаций первого признака (число строк)
m2 – количество градаций второго признака (число столбцов)

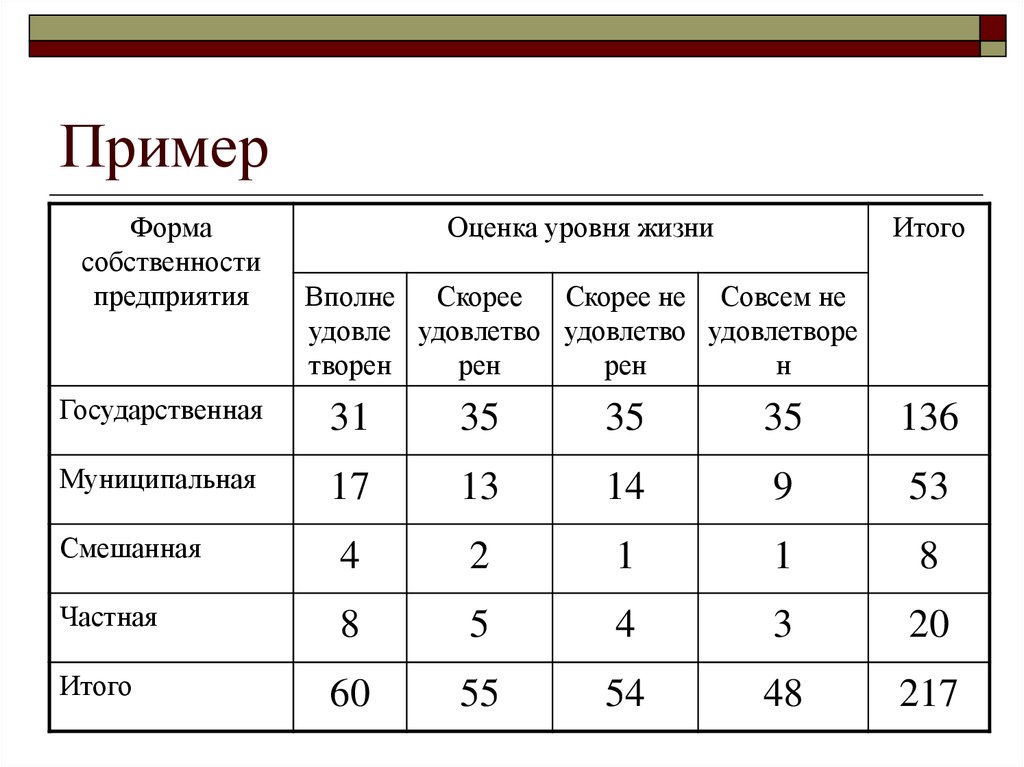
45. Пример

Форма
собственности
предприятия
Оценка уровня жизни
Итого
Вполне Скорее Скорее не Совсем не
удовле удовлетво удовлетво удовлетворе
творен
рен
рен
н
Государственная
31
35
35
35
136
Муниципальная
17
13
14
9
53
Смешанная
4
2
1
1
8
Частная
8
5
4
3
20
60
55
54
48
217
Итого

46. Пример

312 352 352 352 17 2 132 14 2 9 2
1 2 60 55 54 48 60 55 54 48
53
136
4 2 2 2 12 12 82 52 4 2 32
60 55 54 48 60 55 54 48
20
8
0,636 0,249 0,047 0,100 1,032

47. Пример

0.032
KП
0.176
1.032
KЧ
0.032
0.103
4 1 4 1

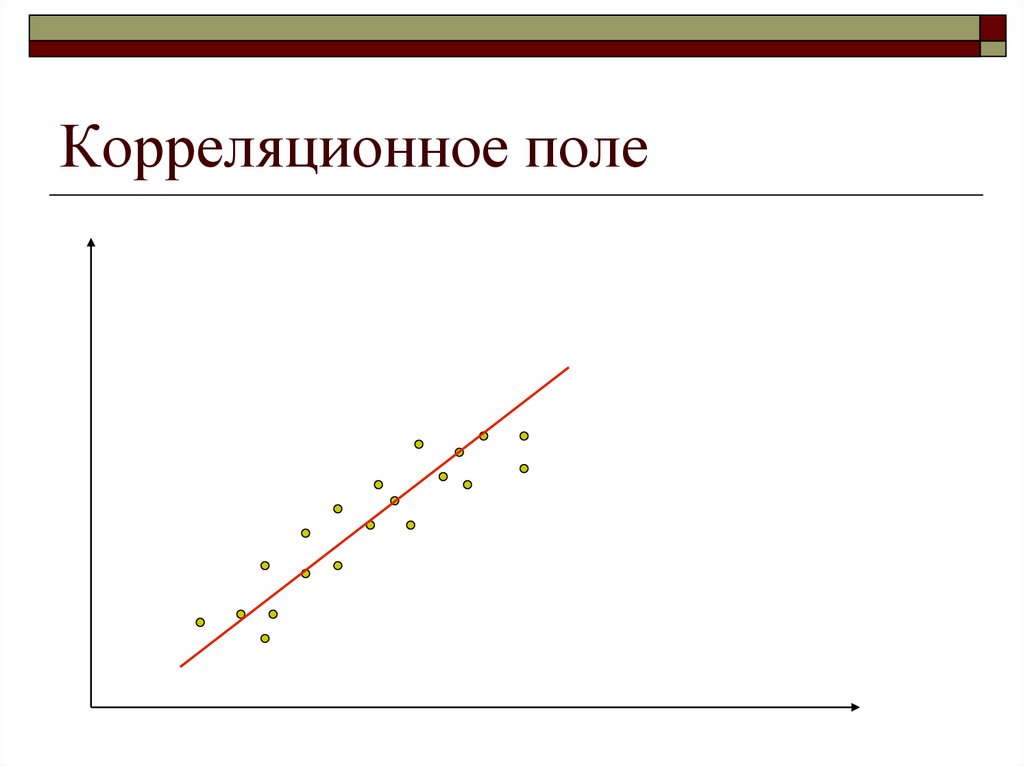
48. Корреляционное поле

49. Корреляционная таблица

X
Y y1
y2
ym
Итого
x1
φ11
φ12
φ1n
∑φij
x2
φ21
φ22
φ2n
∑φij
xn
φn1
φn2
φnm
∑φij
Итого
∑φji
∑φji
∑φji

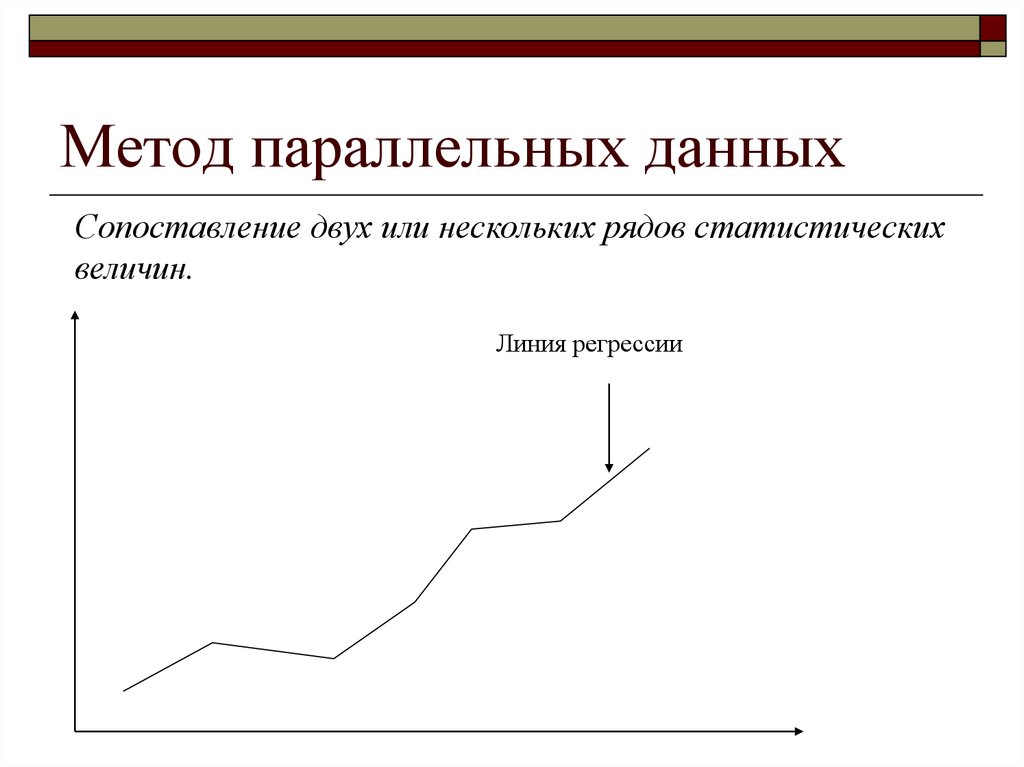
50. Метод параллельных данных

Сопоставление двух или нескольких рядов статистических
величин.
Линия регрессии

51. Метод параллельных данных

Номер
студента
Балл в
сессию, y
Кол-во
пропущенных
семинаров, x
Приведенные параллельные
данные
x
y
1
5
1
1
5
2
3
8
2
5
3
4
3
2
5
4
4
5
3
4
5
3
8
4
4
6
2
10
5
4
7
5
2
6
3
8
4
4
8
3
9
5
2
8
3
10
3
6
10
2

52. Построение уравнения регрессии

Параметры уравнения регрессии определяют из так
называемой системы нормальных уравнений,
отвечающей требованию метода наименьших квадратов
(МНК).
y y
2
x
min

53. Построение уравнения регрессии

Для линейной зависимости:
y a 0 a1 x
n
n
i 1
i 1
S ( y x y ) 2 (a 0 a1 x y ) 2 min

54. Построение уравнения регрессии

Для линейной зависимости:
dS
2 (a 0 a1 y ) * 1 0
da 0
dS
2 (a0 a1 y ) * x 0
da1

55. Построение уравнения регрессии

Для линейной зависимости:
na
a
x
y
0
1
2
a
x
a
x
xy
0
1

56. Построение уравнения регрессии

Для линейной зависимости:
x y x xy
n x ( x )
2
a0
a1
2
2
n xy x y
n x ( x )
2
2

57. Построение уравнения регрессии

Для параболы второго порядка:
y a0 a1 x a2 x
2
na0 a1 x y
2
a0 x a1 x xy
2
3
2
a0 x a1 x x y

58. Построение уравнения регрессии

Для гиперболы:
a1
y a0
x
1
na
a
y
0
1
x
1
1
y
a a
0
1
2
x
x
x

59. Аналитические характеристики производственных функций и их экономическая трактовка.

К числу важнейших аналитических
характеристик относятся:
коэффициент детерминации,
средняя и предельная эффективность
ресурса,
коэффициент эластичности,
норма взаимозаменяемости факторов

60. Аналитические характеристики производственных функций и их экономическая трактовка.

Коэффициент
детерминации
характеризует удельный
вес факторного признака
или признаков в общей
вариации зависимого
показателя.
K Д 100 r
2
<10%
Слабая
10% - 50% Средняя
>50%
Сильная
100%
Полная

61. Аналитические характеристики производственных функций и их экономическая трактовка.

Средняя эффективность ресурса определяется путем
деления соответствующей производственной функции
на объем использованного ресурса. Эффективность
измеряется в единицах результативного показателя в
расчете на единицу ресурса.
y a0
Э a1
x x

62. Аналитические характеристики производственных функций и их экономическая трактовка.

Предельная эффективность ресурса измеряется в
единицах зависимого показателя в расчете на единицу
факторного признака.
dy
Эч
dx
d (a0 a1 x)
Эч
a1
dx

63. Аналитические характеристики производственных функций и их экономическая трактовка.

Эластичность - рассчитывают путем умножения
предельной эффективности ресурса на соотношение
значений фактора и зависимого признака
Эx
y
a1 x
a0 a1 x

64. Оценка значимости параметров взаимосвязи

Стандартная ошибка коэффициента корреляции:
r xy
2
1 rxy
n 2
.
r xy rxy

65. Оценка значимости параметров взаимосвязи

Значимость rxy
t р ас Ч rxy
n 2
2
1 rxy
,
Если tрасч больше теоретического (табличного)
значения критерия Стьюдента (tтабл) для заданного
уровня вероятности и (n - 2) степеней свободы, то
можно утверждать, что rxy значимо.

66. Оценка значимости параметров взаимосвязи

Вывод о правильности выбора вида
взаимосвязи и характеристику значимости
всего уравнения регрессии получают с
помощью F-критерия, вычисляя его расчетное
значение.

67. Оценка значимости параметров взаимосвязи

F р ас Ч
2
R (n m)
2
(1 R )( m 1)
,
где n - число наблюдений;
m - число параметров уравнения регрессии.
Fрасч также должно быть больше Fтеор при v1 = (m
- 1) и v2 = (n - m) степенях свободы.

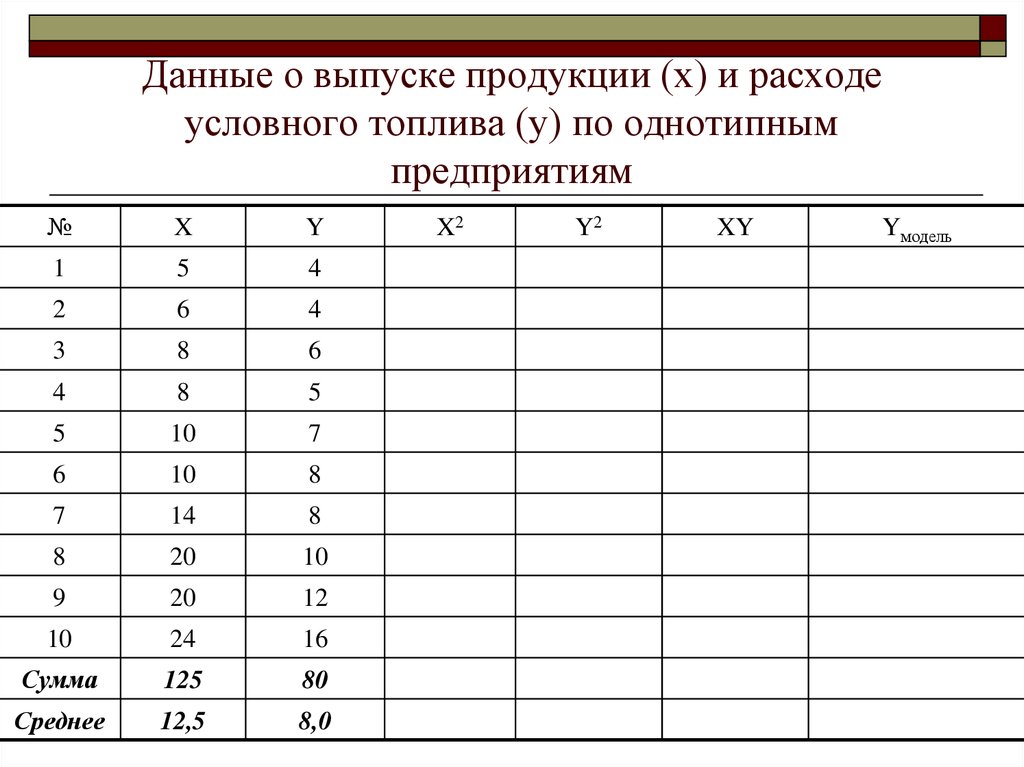
68. Данные о выпуске продукции (х) и расходе условного топлива (у) по однотипным предприятиям

№
X
Y
1
5
4
2
6
4
3
8
6
4
8
5
5
10
7
6
10
8
7
14
8
8
20
10
9
20
12
10
24
16
Сумма
125
80
Среднее
12,5
8,0
X2
Y2
XY
Yмодель

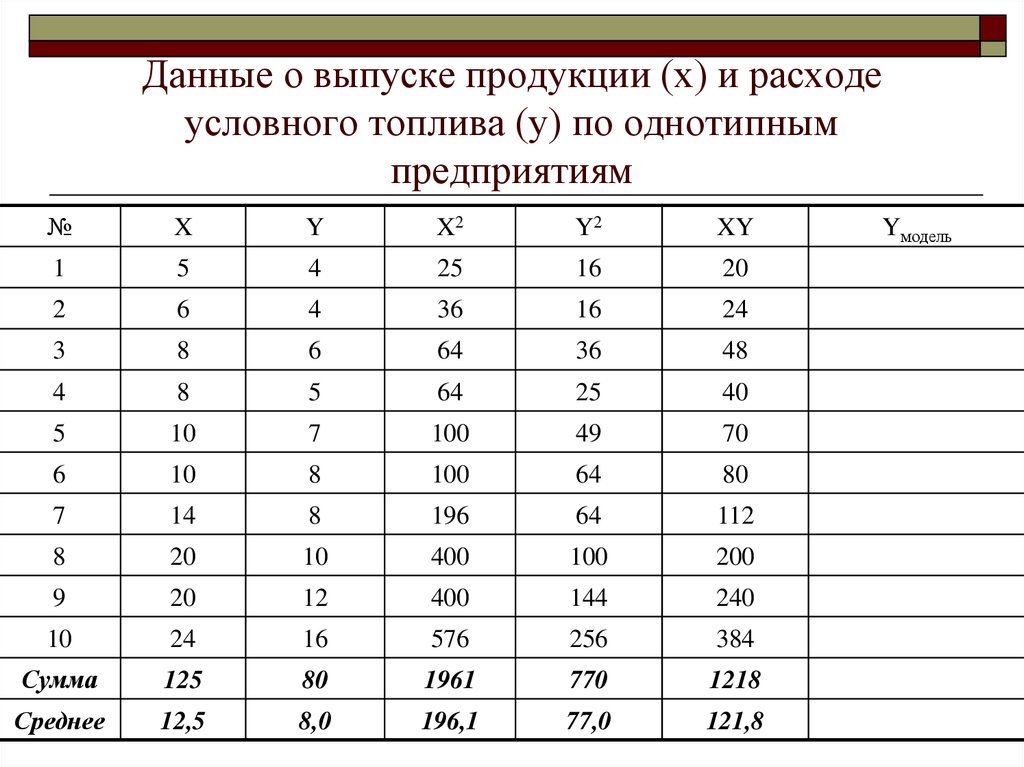
69. Данные о выпуске продукции (х) и расходе условного топлива (у) по однотипным предприятиям

№
X
Y
X2
Y2
XY
1
5
4
25
16
20
2
6
4
36
16
24
3
8
6
64
36
48
4
8
5
64
25
40
5
10
7
100
49
70
6
10
8
100
64
80
7
14
8
196
64
112
8
20
10
400
100
200
9
20
12
400
144
240
10
24
16
576
256
384
Сумма
125
80
1961
770
1218
Среднее
12,5
8,0
196,1
77,0
121,8
Yмодель

70. Коэффициент корреляции

rxy
n x
n x y x y
2
x n y y
2
2
2
10 1218 125 80
10 1961 125 10 770 80
2
2
0.96

71. Определение параметров уравнения регрессии

x y x xy
n x ( x )
2
a0
2
2
1961 80 125 1218
1
.
16
2
10 1961 125

72. Определение параметров уравнения регрессии

a1
n xy x y
n x ( x )
2
2
10 1218 125 80
0
.
55
2
10 1961 125

73. Уравнение регрессии

y a0 a1 x
y 1.16 0.55 x

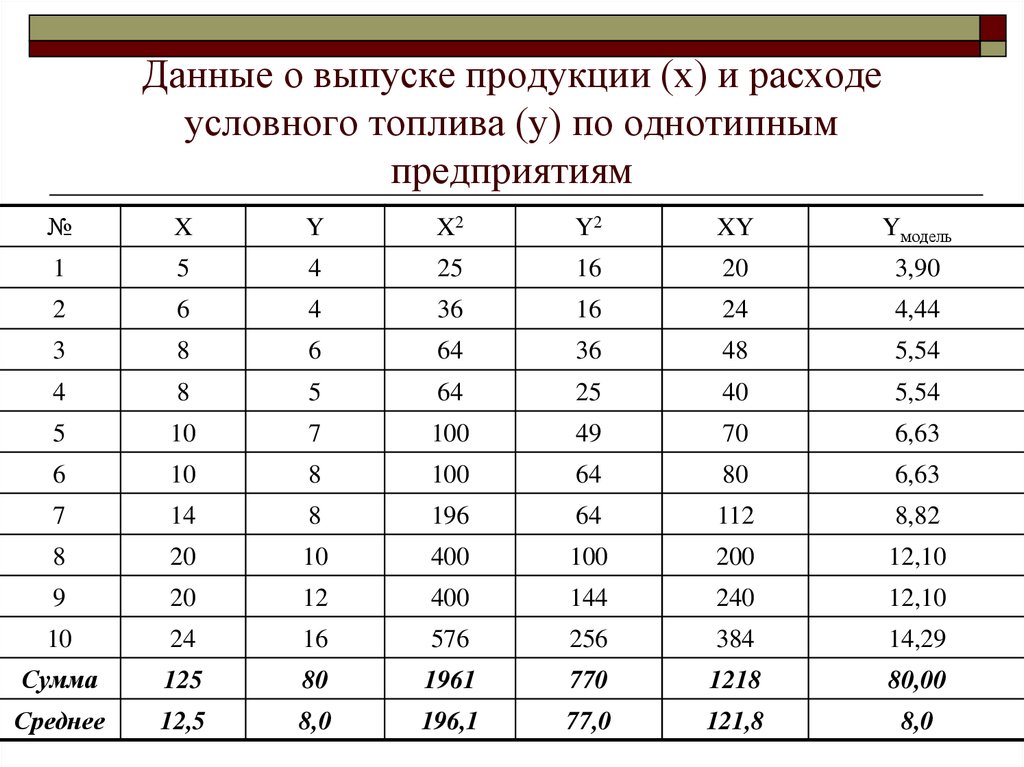
74. Данные о выпуске продукции (х) и расходе условного топлива (у) по однотипным предприятиям

№
X
Y
X2
Y2
XY
Yмодель
1
5
4
25
16
20
3,90
2
6
4
36
16
24
4,44
3
8
6
64
36
48
5,54
4
8
5
64
25
40
5,54
5
10
7
100
49
70
6,63
6
10
8
100
64
80
6,63
7
14
8
196
64
112
8,82
8
20
10
400
100
200
12,10
9
20
12
400
144
240
12,10
10
24
16
576
256
384
14,29
Сумма
125
80
1961
770
1218
80,00
Среднее
12,5
8,0
196,1
77,0
121,8
8,0

75. Аналитические характеристики производственных функций и их экономическая трактовка.

K Д 100 r 100 0.96 91.74
2
y
8
Э
1.56
x 12.5
Эч a1 0.55
2

76. Аналитические характеристики производственных функций и их экономическая трактовка.

Эx 0.55
0.07
y
8
r
xy
1 r
1 0.96
0.10
n 2
10 2
2
xy
2