Статистическое изучение взаимосвязи социально - экономических явлений

1.

2.

Величина
коэффициента
корреляции
Характер связи
До 0,3
Практически отсутствует
0,3 0,5
Слабая
0,5 0,7
Умеренная
0,7 1,0
Сильная

3.

№
студе
нта
Балл в
сессию (y)
Кол-во
пропущенных
семинаров (x)
1
2
3
4
5
6
7
8
9
5
3
4
4
3
2
5
4
5
10
3
Присоединенные
параллельные данные
x
y
1
8
3
5
8
10
2
4
2
1
2
2
3
4
5
6
8
8
5
5
5
4
4
4
3
3
3
6
10
2

4.

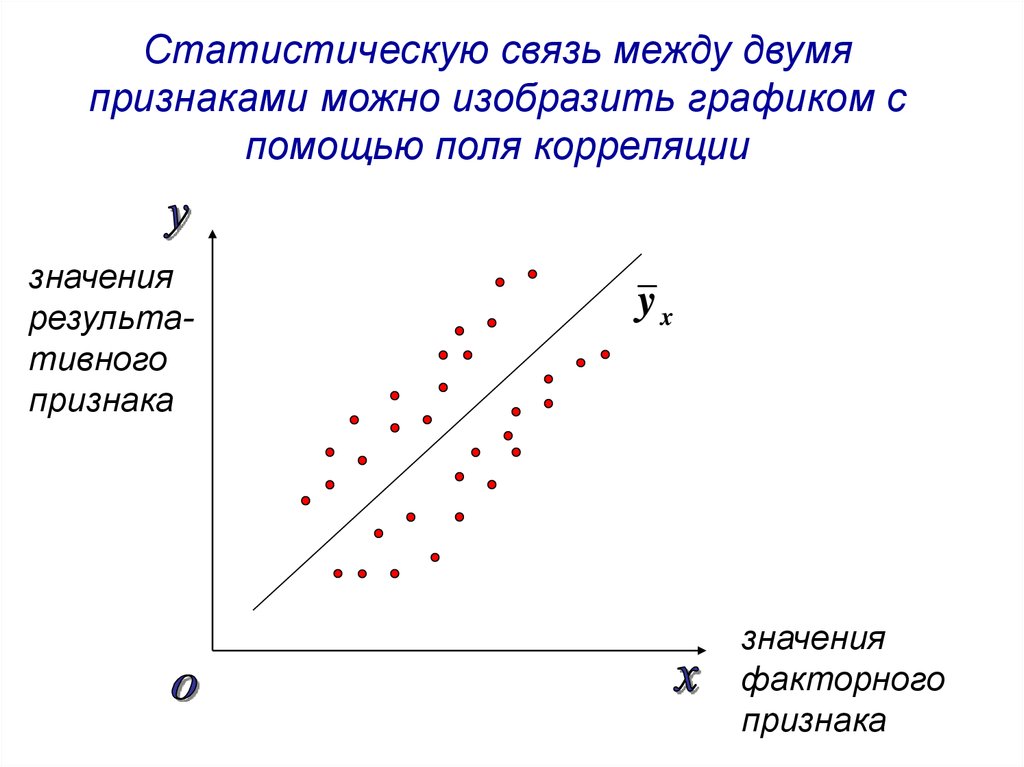
Статистическую связь между двумя
признаками можно изобразить графиком с
помощью поля корреляции
значения
результативного
признака
yx
значения
факторного
признака

5.

y
5
4
3
2
2
4
6
8
10
Кол-во пропущенных семинаров
x

6.

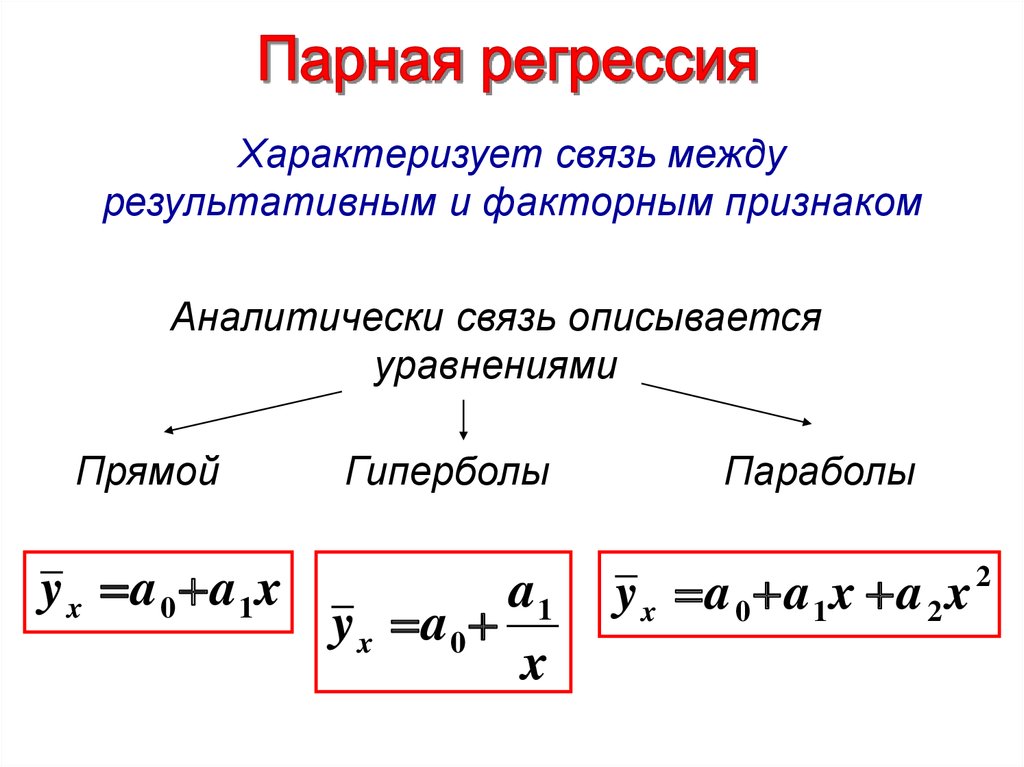
Характеризует связь между
результативным и факторным признаком
Аналитически связь описывается
уравнениями
Прямой
y x a 0 a1x
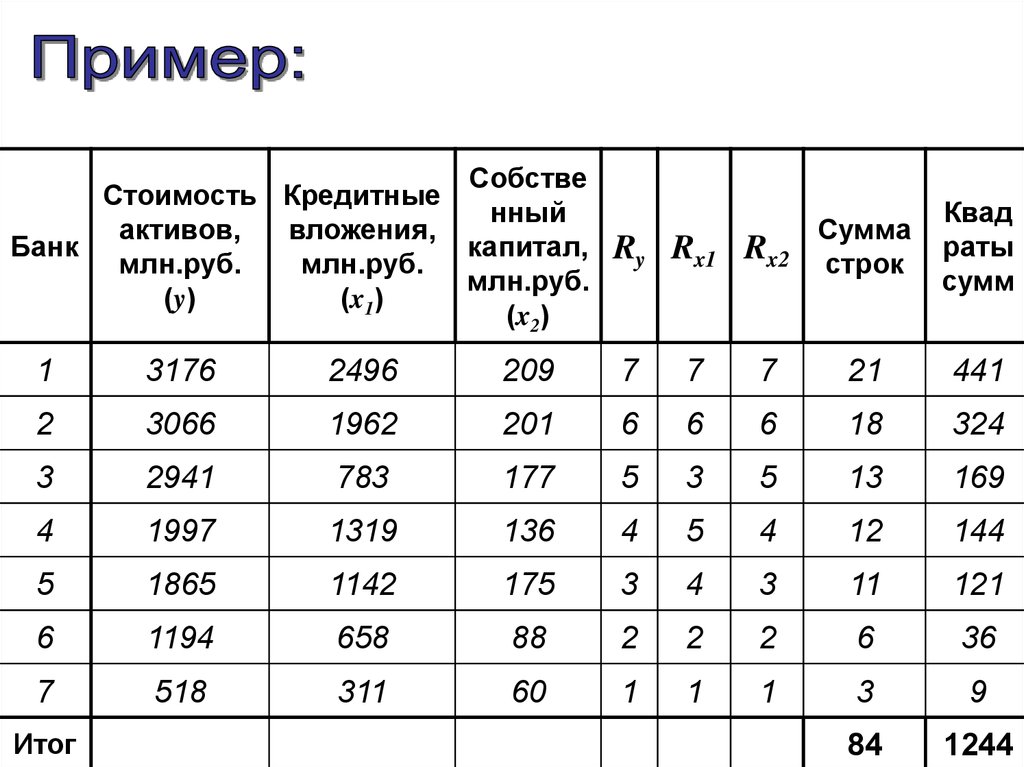
Гиперболы
a1
y x a 0
x
Параболы
y x a 0 a1x a 2 x
2

7.

S ( y y x ) min
2
Система уравнений для нахождения
параметров линейной парной регрессии:
na0 a1 x y
2
a0 x a1 x xy
n
– объем исследуемой совокупности
(число единиц наблюдения)

8.

№
п/п
Число
профессион
алов, чел.
(x)
Совокупная
выручка,
млн. руб. (y)
x2
xy
yx
1
23
2,62
529
60,26
2,661
2
32
3,04
1024
97,28
2,967
3
50
3,15
2500
157,50
3,579
4
53
3,83
2809
202,99
3,681
5
55
3,58
3025
196,90
3,749
6
58
4,08
3364
236,64
3,851
7
59
4,09
3481
241,31
3,885
8
62
4,20
3844
260,40
3,987
9
69
4,18
4761
288,42
4,225
10
75
4,24
5625
318,00
4,429
Итог:
536
37,01
30962
2059,7
37,010

9.

10a0 536a1 37,01
536a0 30962a1 2059,7
a0 1,879; a1 2059,7
y x 1,879 0,034 х
При увеличении числа профессионалов на 1
человека её совокупная выручка
увеличивается в среднем на 34 тыс. руб.

10.

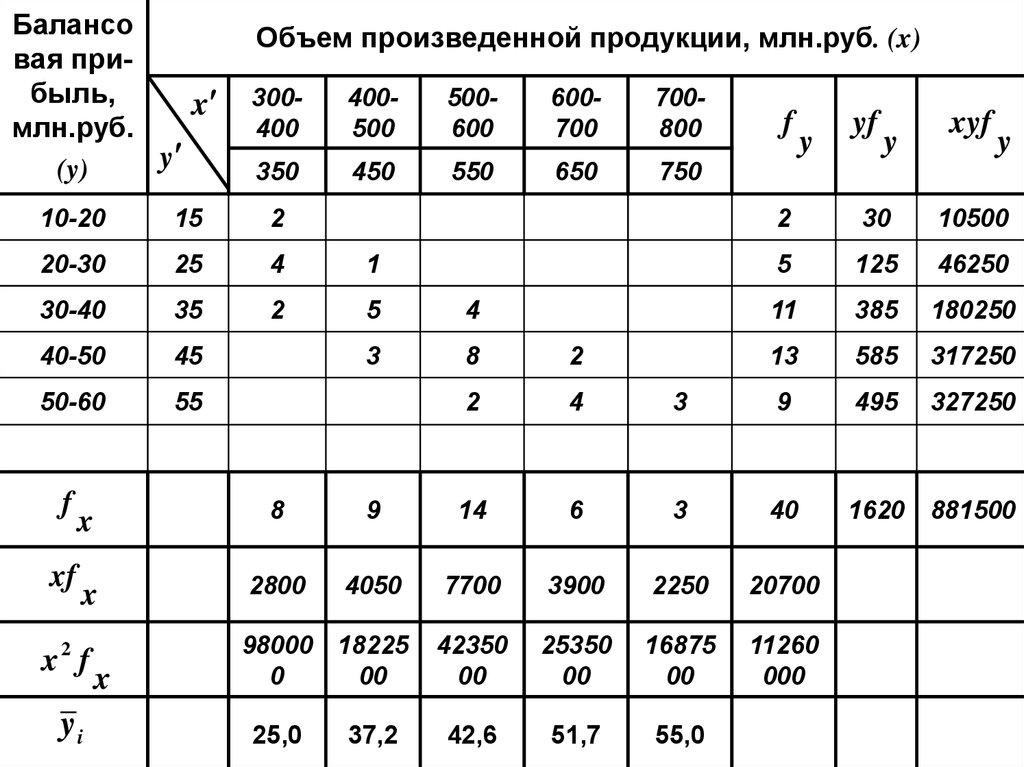
Балансо
вая прибыль,
x
млн.руб.
y
(y)
Объем произведенной продукции, млн.руб. (x)
300400
400500
500600
600700
700800
350
450
550
650
750
10-20
15
2
20-30
25
4
1
30-40
35
2
5
4
40-50
45
3
8
2
50-60
55
2
4
f
xf
f
y
5
125
46250
11
385
180250
13
585
317250
3
9
495
327250
1620 881500
14
6
3
40
x
2800
4050
7700
3900
2250
20700
98000 18225
0
00
42350
00
25350
00
16875
00
11260
000
42,6
51,7
55,0
25,0
37,2
y
10500
9
yi
xyf
30
8
x
y
2
x
x2 f
yf

11.

Считая, что зависимость описывается
уравнением прямой, коэффициенты а0 и а1
определяются из системы нормальных
уравнений:
na0 a1 xf yf
x
y
2
a
x
f
a
x
f xyf
0 x
1
x
xy

12.

По 1ой группе:
300 400
x1
350
2
yf y 15 * 2 30
xf x 350 * 8 2800
xyf y 350 * 15 * 2 10500
x f x 350 * 8 980000
2
2
2
yi 15 * 2 25 * 4 35 * 25,0
8

13.

По 2ой группе:
400 500
x 2
450
2
yf y 25 * 5 125
xf x 450 * 9 4050
xyf y 350 * 25 * 4 450 * 25 * 1 46250
x f x 450 * 9 1822500
2
2
3
yi 25 * 1 35 * 5 45 * 37,2
9

14.

40a0 20700a1 1600
20700a0 11260000a1 881500
a0 0,9; a1 0,08
y x 0,9 0,08 x
При увеличении объема выпуска на 1
млн.руб. балансовая прибыль в среднем
увеличивается на 80 тыс. руб.

15.

Если связь между признаками
криволинейная и описывается уравнением
параболы 2ого порядка, то система
нормальных уравнений имеет вид:
na0 a1 x a0 x 2 y
2
3
a0 x a1 x a2 x xy
2
3
4
2
a0 x a1 x a2 x yx

16.

Оценка обратной зависимости между х и у
осуществляется на основании уравнения
гиперболы
1
na0 a1 x y
1
1
y
a
a
0
1
2
x
x
x

17.

Характеризующих зависимости между
социально-экономическими движениями
- Линейная
y1, 2,.., k a 0 a 1 x1 a 2 x2 ... a k xk
- Степенная
y1, 2,.., k a 0 x 1 * x 2 ... xk
a1
a2
ak

18.

- Показательная
y1,2,.., k ea a x
0
1 1
a 2 x2 ... a k xk
- Параболическая
y1, 2,.., k a 0 a1x 1 a 2 x 2 ... a k x k
2
2
- Гиперболическая
y1, 2,.., k
ak
a1 a 2
a 0
...
x1 x 2
xk
2

19.

№ банка
1
2
3
4
5
6
7
Итого
Сумма
активов(y)
3176
3066
2941
1997
1865
1194
518
14757
Кредитные
вложения,
(x1)
2496
1962
783
1319
1142
658
311
8671
Собственн
о капита,
(x2)
209
201
177
136
175
88
60
1046
yx 1
7927296
6015492
2302803
2634043
2129830
785652
16198
21956214
x 12
6230016
3849444
613089
1739761
1304164
432964
96721
14266159
y2
10086976
9400356
86494481
3988009
3478225
1425636
268324
37297007
x1 x2
521664
394362
138591
179384
199850
57904
18660
1510415
x 22
43681
40401
31329
18496
30625
7744
3600
175876
yx2
663784
616266
520557
271592
326375
105072
31080
2534726
yx
3153*
3000
2554
1886
2533
1057
574
14757

20.

Система нормальных уравнений имеет вид:
na0 a1 x1 a2 x2 y
2
a
x
a
x
0 1 1 1 a2 x1 x2 yx1
2
2
a
x
a
x
x
a
x
yx
0 2
1 1 2
2 2
7a0 8671a1 1046a2 14757
8671a0 14266159a1 1510415a2 21956214
1046a 1510415a 175876a 2534726
0
1
2

21.

* 3153 443,4 0,0368 2496 16,77 209
a 0 443,4;
a1 0,0368
a2 16,77
y x1, x2 443,4 0,368 x1 16,77 x2
При увеличении кредитных вложений на 1
млн.руб. и собственного капитала
коммерческих банков на 1 млн.руб. стоимость
их активов в среднем увеличивается на 0,0368
млн.руб. и 16,77 млн.руб.

22.

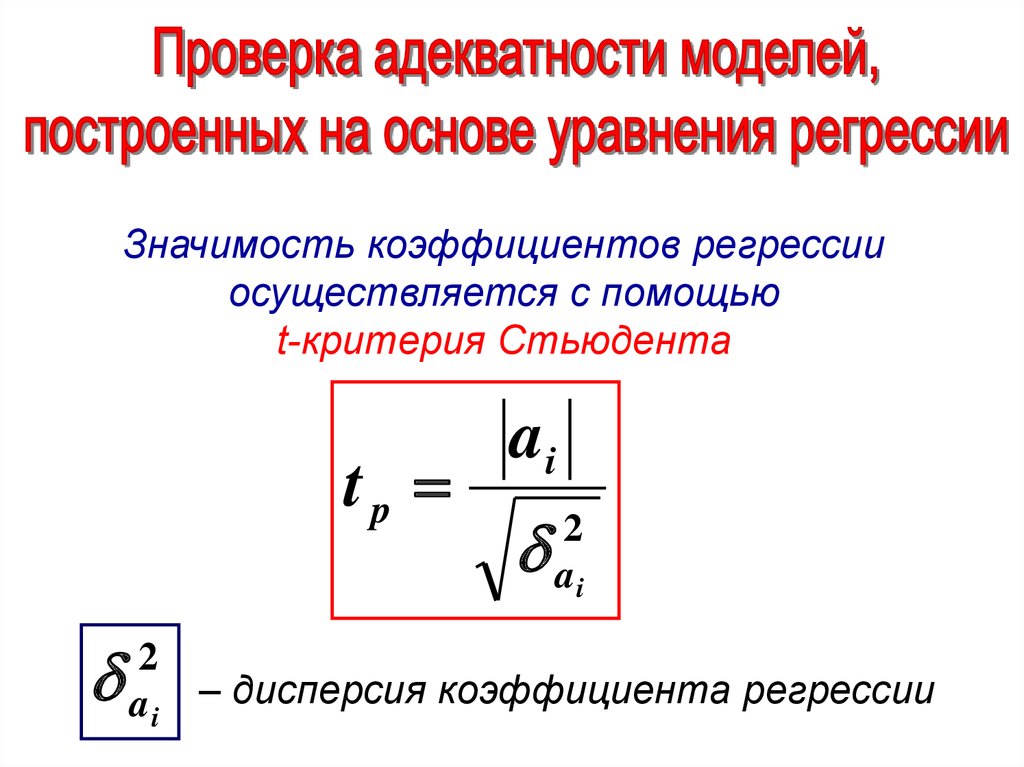
Значимость коэффициентов регрессии
осуществляется с помощью
t-критерия Стьюдента
tp
2
ai
ai
2
ai
– дисперсия коэффициента регрессии

23.

Параметр модели признается
статистически значимым, если
t p t кр ( ; n k 1)
– уровень значимости проверки гипотезы о
равенстве нулю параметров, измеряющих
связь
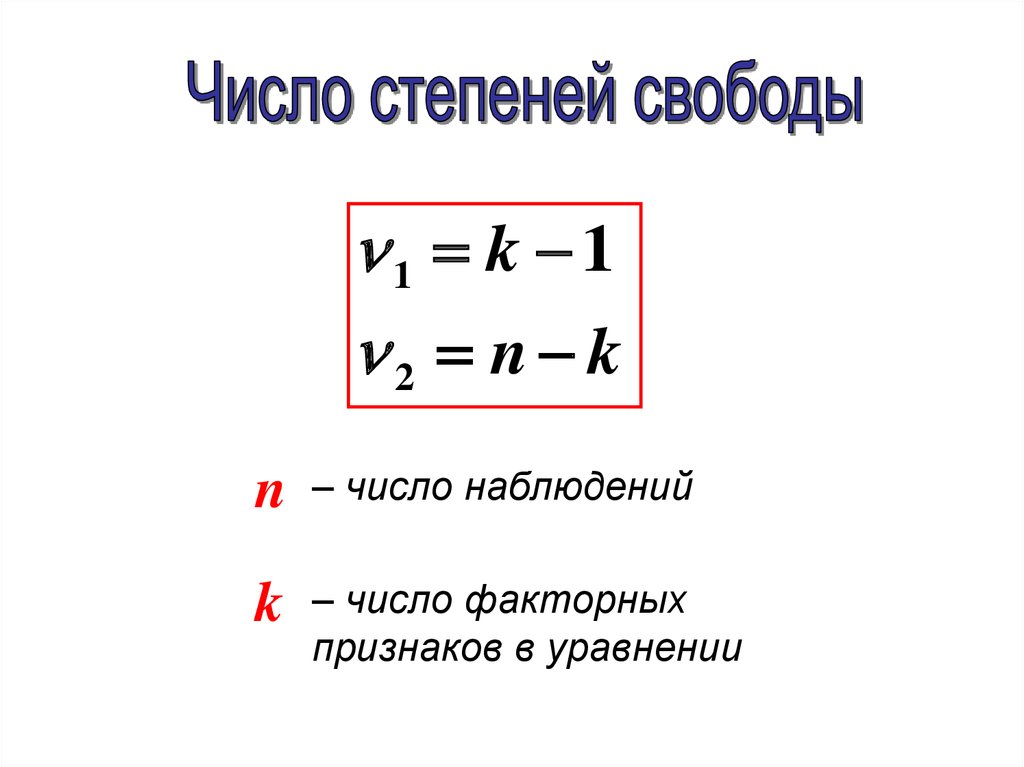
n k 1
– число степеней свободы,
которое характеризует число
свободно варьирующих
элементов совокупности

24.

2
ai
2
y
k
y2 – дисперсия результативного признака
k
– число факторных признаков в уравнении

25.

a
i
y 1 R
2
x n 1 Ri
i
Ri – величина множественного коэффициента
корреляции по фактору xi с остальными
факторами

26.

Проверка адекватности всей модели
осуществляется с помощью расчета
F-критерия и величины средней ошибки
аппроксимации E
Если
F p F
при
0,05 или 0,01
То H 0 – гипотеза о несоответствии
заложенных в уравнение регрессии связей
реально существующим отвергается

27.

1 k 1
2 n k
n
– число наблюдений
k
– число факторных
признаков в уравнении

28.

y y1, 2,.., k
1
E
100
n
y
не должно превышать 12-15%

29.

Э xi
xi
ai
y
x i – среднее значение соответствующего
факторного признака
y – среднее значение результативного
признака
ai – коэффициент регрессии при
соответствующем факторном признаке

30.

По данным о сумме актов (y) кредитных вложений (x1) и
величине собственного капитала (х2) коммерческих
банков рассчитать коэффициент эластичности
Э x1
x1
1238,7
ai
0,0368
0,02
y
2108,1
ai 0,0368
8671
x1
1238,7
7
14757
y
2108,1
7

31.

Э x2
x2
149,4
ai
16,77
1,19
y
2108,1
ai 16,77
1046
x2
149,4
7
При увеличении кредитных вложений и
собственного капитала на 1% стоимость актов
в среднем возрастает собственно
на 0,02 и 1,19%

32.

d
ryx
x
i
i
xi
ryxi
x
i
– парный коэффициент корреляции между
результативным и i-ным факторным
признаками
– соответственный коэффициент
уравнения множественной регрессии в
стандартизированном масштабе

33.

Рассчитать частный коэффициент
детерминации для
фактора x1 – кредитного вложения
d
x1
ryx1
1) yx 1
yx1 y x 1
ryx1
x1 y
x
1
yx
1
n
21956214
3136602
7
2) y 2108,1 ; x1 1238,7

34.

3)
x
2
1
x
2
x1
1
y
y y
2
2
14266159
2
1238,7 709,7
7
37297007
2
2108,1 949,6
7
3136602 2108,1 1238,7
4) ryx1
0,78
709,7 949,6
x1
709,7
5) xi ax1
0,0368
0,03
y
949,6

35.

6)
d
x1
0,78 0,03 0,02
2% вариации стоимости активов
объясняется изменением величины
кредитных вложений

36.

Рассчитать частный коэффициент
детерминации для
фактора x2 – собственный капитал
1)
y 2108,1 ; x2 149,4
2534726
362103
2) yx 2
7

37.

3)
x
2
175876
2
149,4
7
25125 22320 53
y 949,6
4)
362103 2108,1 149,4
ryx2
0,94
53 949,6
5)
53
x2 16,77 949,6 0,94

38.

6)
d
x2
0,94 0,94 0,88
На 88% изменение стоимости
активов объясняется изменением
собственного капитала

39.

– используется для более точной оценки
влияния каждого факторного признака на
моделируемый
Q x Э x i x i
i
x – коэффициент вариации
i
соответствующего факторного признака

40.

Рассчитать Qx1 для
фактора x1 – кредитного вложения
1) Эx 0,02
1
2)
x
709,7
100%
100% 57%
x1
x1
1238,7
1
Qx1 0,02 0,57 0,01

41.

Рассчитать Qx2 для
фактора x2 – собственный капитала
1) Эx 1,19
2
2)
53
100% 35,5%
x 2 149,4
Qx2 1,19 0,355 0,42

42.

Различные модификации ф-ии для расчета
данного коэффициента:
1)
2)
rxy
rxy
( x x )( y y )
x y
xy x y
x y

43.

При изучении совокупностей малого объема:
3)
4)
rxy
n xy x y
n x 2 x 2 n y 2 y 2
rxy
2 x y
2
x
2
y
2
x y
(Через дисперсии
слагаемых)

44.

x
rxy ai
y
i
ai
x
1 r 1
– коэффициент регрессии в уравнении связи
i
– среднее квадратичное отклонение,
соответствующее статистически
существенным факторным признакам

45.

Значение
линейного
коэффициента
связи
Характер связи
r=0
Отсутствует
0<r<1
Прямая
-1<r<0
Обратная
r=1
Интерпретация связи
С увеличением x
увеличивается y
С увеличением x
уменьшается y
Каждому значению
факторного признака
Функциональная
строго соответствует 1
значение результативного
признака

46.

Значимость линейного коэффициента
корреляции проверяется
на основе t-критерия Стьюдента
tp
2
xy
r
1 r
2
xy
( n 2)
при n<50
rxy
1 r
2
xy
( n 2)

47.

Значимость линейного коэффициента
корреляции проверяется
на основе t-критерия Стьюдента
tp
r
1 r
2
при n>100
n

48.

Оценить тесноту связи между стоимостью
активов (y) и кредитными вложениями (x1)
1)
ryx
1
yx y x
x y
0,78
7 21956214 8671 14757
2) rxy
7 14266159 86712 7 37297007 14757 2
rxy 0,78

49.

Проверка значимости:
tp
0,78 2
1 0,78
2
(7 2) 3,72
0,05
n 1 7 1 6
t кр 2,447
t р 3,72 t кр 2,447
Коэффициент корреляции значим

50.

2
2
2
– общая дисперсия
2
– межгрупповая дисперсия

51.

2
2
2
2
0 1
– дисперсия выровненных значений
результативного признака
– дисперсия эмпирических (фактических)
значений результативного признака

52.

По данным группировки 40 предприятий легкой
промышленности по величине балансовой прибыли и
объему произведенной продукции определить
эмпирическое корреляционное отношение
yf
y
f
y
y
y
1620
40,5
40
y y
2
2
y f
f
2
y
y
yf y
f
y
2
152 2 252 5 352 11 452 13 552 9
40,52
40
1765 1640,25 124,8

53.

yi y ( yi y ) ( yi y ) f x
2
2
yi
fx
25,0
8
-15,5
240,25
1922,0
37,2
9
-3,3
10,89
98,01
42,6
14
2,1
4,41
61,74
51,7
6
11,2
125,44
752,64
55,0
3
14,5
210,25
630,75
Итого
40
3465,4

54.

2
3465,4
36,6
40
86,6
0,83
124,8
Связь сильная

55.

R
2
2
ост .
y
x1 x 2 ...
1
2
ост .
2
– общая дисперсия результативного
признака
– остаточная дисперсия

56.

• В случае оценки связи между результативным
и 2мя факторными признаками определяется по
формуле:
R
y
x1 x 2
r
r
2
yx1
r
2
yx 2
2ryx1 ryx 2 rx1 x 2
1 r
2
x1 x 2
– парные коэффициенты корреляции
между признаками

57.

• Используя парные коэффициенты rij и
коэффициенты регрессии в стандартизированном
масштабе i , рассчитывается по формуле:
Rx1 x2 ... xk
1ryx 2 ryx ... k ryx
1
0 R 1
2
k

58.

Чтобы оценить общую вариацию
результативности признака в зависимости от
факторных признаков, коэффициент
корректируется на основании выражения:
ˆ
R
y
x1 x2 ... xk
k
n
n 1
1 (1 R )
n k 1
2
– число факторных признаков
– число наблюдений
Не корректируется, если:
n k
20
k

59.

Проверка значимости коэффициента
осуществляется на основании
Fp
1 2
R y
2 x1 x 2
1
2
(1 R y )
n 3
x1 x 2

60.

Гипотеза H 0 о незначимости
коэффициента H 0 : R 0 отвергается
Если:
F p Fкр ( ; 1 2; 1 n 3)

61.

По данным о сумме актов кредитных вложений и
величине собственного капитала коммерческих банков
рассчитать коэффициент множественной корреляции и
проверить его значимость:
1) ryx1 0,78
3)
2) ryx 2 0,95
r
1510415 1238,7 149,4
x1 x 2 x1 x2
7
x1 x2
709,7 53
r
0,82
x1 x 2
x1 x 2

62.

4) R
R
y
x1 x 2
y
x1 x 2
0,78 2 0,95 2 2 0,78 0,95 0,82
1 0,82 2
0,95
Связь сильная, факторы x1 и x2 практически
полностью обуславливают величину y.

63.

Проверка значимости:
Fp
1
0,95 2
2
1
(1 0,95 2 )
7 3
F p 18,51 Fкр 6,94
0,45125
18,51
0,02438
( 0,05; 1 2; 1 7 3)
Гипотеза о незначимости коэффициента отвергается

64.

r
1, 2 , 3 , 4 ,..., k
r
1, 2 , 3 , 4 ,..., k 1
(1 r 2
r1,k , 3,..., k 1 r2,k , 3,..., k 1
1, k , 3 ,..., k 1
) (1 r 2
2 , k , 3 ,..., k 1
)

65.

В случае зависимости y от 2x факторных признаков:
r
r
yx1
x2
yx 2
x1
r
yx1
rx1 x2 ryx2
(1 ryx2 ) (1 rx2 x )
2
r
1 2
rx1 x2 ryx1
yx 2
(1 r
2
yx1
) (1 r
2
x1 x 2
)
r – парные коэффициенты корреляции
между указанными в индексе переменными

66.

По данным о сумме актов кредитных вложений и
величине собственного капитала коммерческих банков
рассчитать частные коэффициенты корреляции и
проверить их значимость:
1) ryx1 0,78
2) ryx 2 0,95
3) rx1 x 2 0,82

67.

4)
5)
r
r
yx1
x2
yx 2
x1
0,78 0,95 0,82
(1 0,95 ) (1 0,82 )
2
2
0,95 0,78 0,82
(1 0,782 ) (1 0,822 )
0,006
0,87

68.

6)
r
r
x1 x 2
y
x1 x 2
y
r
x1 x 2
ryx1 ryx 2
(1 ryx2 ) (1 ryx2 )
1
2
0,82 0,78 0,95
(1 0,78 2 ) (1 0,95 2 )
0,4

69.

Проверка значимости:
1) t
yx1
p ( x2 )
t
yx1
p ( x2 )
3) t
x1 x 2
(
)
p
y
n 3
2
1 ryx
1
0,006 7 3
2) t
yx 2
(
)
p
x1
ryx1
1 0,0062
0,012
0,87 2
1 0,87
2
0,4 2
1 0,4 2
3 ,6
0,87

70.

Проверка значимости:
4)
t кp 2,776
0,05
n 3 4
Не все полученные коэффициенты корреляции значимы

71.

a
b
a+b
c
d
c+d
a+c
b+d
a+b+c+d

72.

ad bc
ka
ad bc
kk
ad bc
( a b )( b d )( a c )( c d )
k k ka
k a 0 ,5
k k 0, 3
всегда
Связь считается
подтвержденной

73.

Из них
Семейное
положение
Число
Не
вкладчиков, Имеющие
имеющие
чел.
сбережени
сбережен
я
ия
Одинокие
400
250
150
Семейные
1250
800
450
Итого:
1650
1050
600

74.

250 450 150 800
ka
250 450 150 800
112500 120000
7500
0,03
112500 120000
232500
250 450 150 800
kk
( 250 150)(150 450)( 250 800)( 800 450)
112500 120000
7500
0,01
400 600 1050 1250 561248,7

75.

y
I
II
III
Итого:
I
…
…
nyx
nx
II
…
…
nx
III
…
…
nx
Итого:
ny
ny
x
ny
nx

76.

kП
kЧ
2
1 2
2
k1 1 k 2 1

77.

2
– определяется как сумма отношений
квадратов частот каждой клетки
таблицы к произведению итоговых
частот соответствующего столбца и
строки минус 1
2
n
2
xy
nx n y
1

78.

k1 – число значений (групп) 1ого признака
k2 – число значений (групп) 2ого признака
1
2
n
2
xy
nx
ny
n
2
xy
ny
nx

79.

Образова
ние
Высшее
Неполное
высшее
Среднее
специаль
ное
Среднее
общее
Итого:
Категории сотрудников
Итого:
Руковод
Служащие Рабочие
ители
10
30
5
45
7
25
10
42
2
15
50
67
1
10
25
36
20
80
90
190

80.

1 2
10 2
30 2
52
72
25 2
10 2
80
90 20
80
90
20
45
42
22
15 2
50 2
12
10 2
25 2
80
90 20
80
90
20
67
36
5 11,25 0,28 2,45 7,81 1,11
45
42
0,2 2,81 27,78 0,05 1,25 6,94
67
36
0,367 0,271 0,459 0,229 1,326

81.

0,326
2
kП
kЧ
0,326
1,326
0,246 0,496
0,326
4 - 1 3 - 1
0,326
0,365
2,449
Связь близка к умеренной

82.

Через расчет 2 критерия Пирсона
kП
2
2
2
n 2
2
n
xy
n
1
xy n x n y
-наиболее распространенный критерий согласия,
используемый для проверки статистической
гипотезы о виде распределения

83.

(По данным таблицы об уровне
образования сотрудников)
2
2
2
2
2
2
10
30
5
7
25
10
2 190
20 45 80 45 90 45 20 42 80 42 90 42
22
15 2
50 2
12
10 2
25 2
1
20 67 80 67 90 67 20 36 80 36 90 36
190 0,111 0,25 0,006 0,058 0,186 0,026 0,003 0,042
0,415 0,001 0,035 0,193 1 190 1,326 1 61,94
kП
61,94
190 61,94
61,94
0,496
251,94

84.

kЧ
2
n (k1 1)( k 2 1)
k1 – число строк в таблице
k2
– число граф в таблице
n
– число наблюдений

85.

(По данным таблицы об уровне
образования сотрудников)
kЧ
61,94
190 4 1 3 1
61,94
190 3 2
61,94
0,133 0,365
190 2,449
Связь средняя

86.

r
y2 y1
y
pq
z

87.

y1 и y2 – средние в группах
y – среднее квадратичное
отклонение фактических
значений признака от
среднего уровня
p – доля первой группы
q – доля второй группы
z
– табулированные значения zраспределения в зависимости от p

88.

(Зависимость возраста и
социального положения эмигрантов)
Возраст, лет
Основные
категории
потенциальных
эмигрантов
50 и
Всего,
больше
чел.:
До 30
30-40
40-50
25
35
45
55
Руководители
5
30
39
26
100
Рабочие
21
38
28
13
100
Итого:
26
68
67
39
200

89.

25 5 35 30 45 39 55 26
y1
43,6
100
25 21 35 38 45 28 55 13
y2
38,3
100
yобщ
25 26 35 68 45 67 55 39
40,95
200
( 25 40,95)2 26 ( 35 40,95)2 68
y
26 68 67 39
(45 40,95)2 67 (55 40,95)2 39
9,439

90.

100
p
0,5
200
q 0,5
z 0,3977
38,3 - 43,6
0,5 0,5
r
0,4
9,439
0,3977
Связь умеренная

91.

kФ
с н
c н
c – число совпадений знаков
отклонений
Н
– число несовпадений
знаков отклонений

92.

1 kФ 1
kФ 1 – связь между признаками
функциональная
kФ 0 – связь отсутствует
kФ 1;0
kФ 0;1
– связь обратная, с
увеличением/снижением х
снижается/увеличивается у
– связь прямая, с
увеличением/снижением х
увеличивается/снижается у

93.

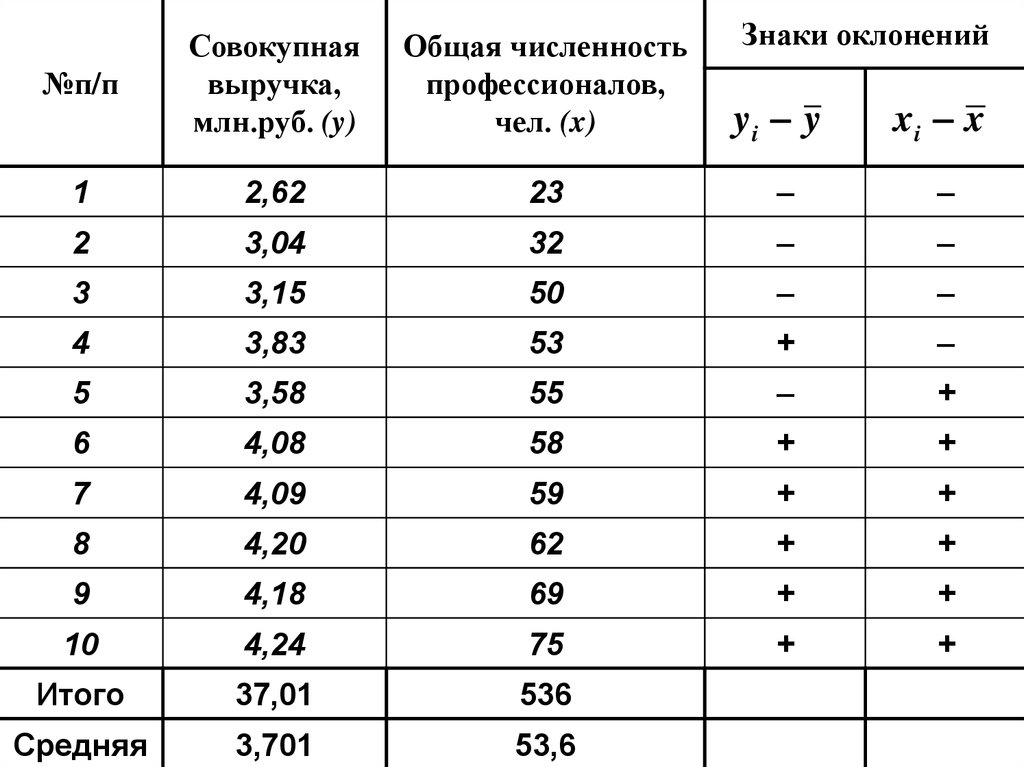
Знаки оклонений
№п/п
Совокупная
выручка,
млн.руб. (y)
Общая численность
профессионалов,
чел. (x)
yi y
xi x
1
2,62
23
–
–
2
3,04
32
–
–
3
3,15
50
–
–
4
3,83
53
+
–
5
3,58
55
–
+
6
4,08
58
+
+
7
4,09
59
+
+
8
4,20
62
+
+
9
4,18
69
+
+
10
4,24
75
+
+
Итого
37,01
536
Средняя
3,701
53,6

94.

kФ
8 2
0,6
8 2
Связь между совокупной выручкой и
численностью профессионалов
аудиторско-консультационных фирм
прямая и умеренная

95.

x
y
1
6 d
2
i
n( n 1)
2
2
di – квадрат разности рангов
n – число наблюдений
(число пар рангов)

96.

Значимость коэффициента Спирмэна
проверяется
на основе t-критерия Стьюдента
tp x
y
n 2
2
1 x y
t p t кp ( ; k n 2)
Значение
статистически
существенно

97.

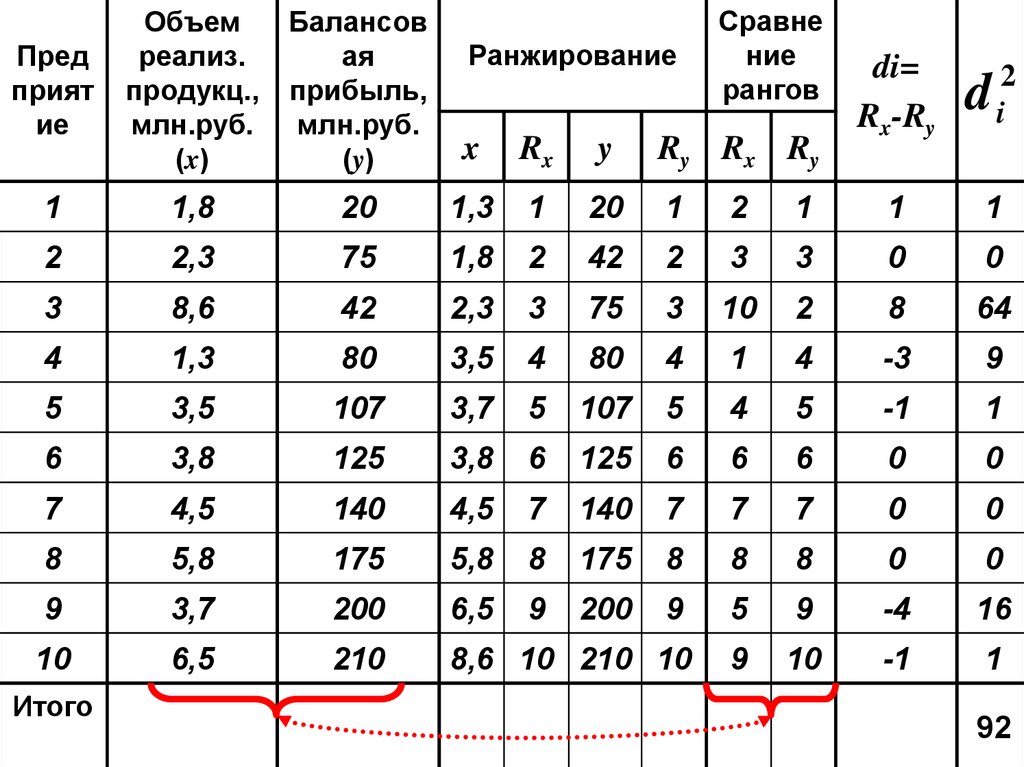
Сравне
ние
рангов
Пред
прият
ие
Объем
реализ.
продукц.,
млн.руб.
(x)
Балансов
ая
прибыль,
млн.руб.
(y)
x
Rx
y
1
1,8
20
1,3
1
20
1
2
1
1
1
2
2,3
75
1,8
2
42
2
3
3
0
0
3
8,6
42
2,3
3
75
3
10
2
8
64
4
1,3
80
3,5
4
80
4
1
4
-3
9
5
3,5
107
3,7
5
107
5
4
5
-1
1
6
3,8
125
3,8
6
125
6
6
6
0
0
7
4,5
140
4,5
7
140
7
7
7
0
0
8
5,8
175
5,8
8
175
8
8
8
0
0
9
3,7
200
6,5
9
200
9
5
9
-4
16
10
6,5
210
8,6 10 210 10
9
10
-1
1
Итого
Ранжирование
Ry Rx Ry
di=
Rx-Ry
d
2
i
92

98.

x
y
6 92
552
1
1
0,44
2
10(10 1)
990
Связь близка к умеренной

99.

xy
2S
n( n 1)
S – сумма разностей между числом
последовательностей и числом
инверсий по 2ому признаку
n – число наблюдений

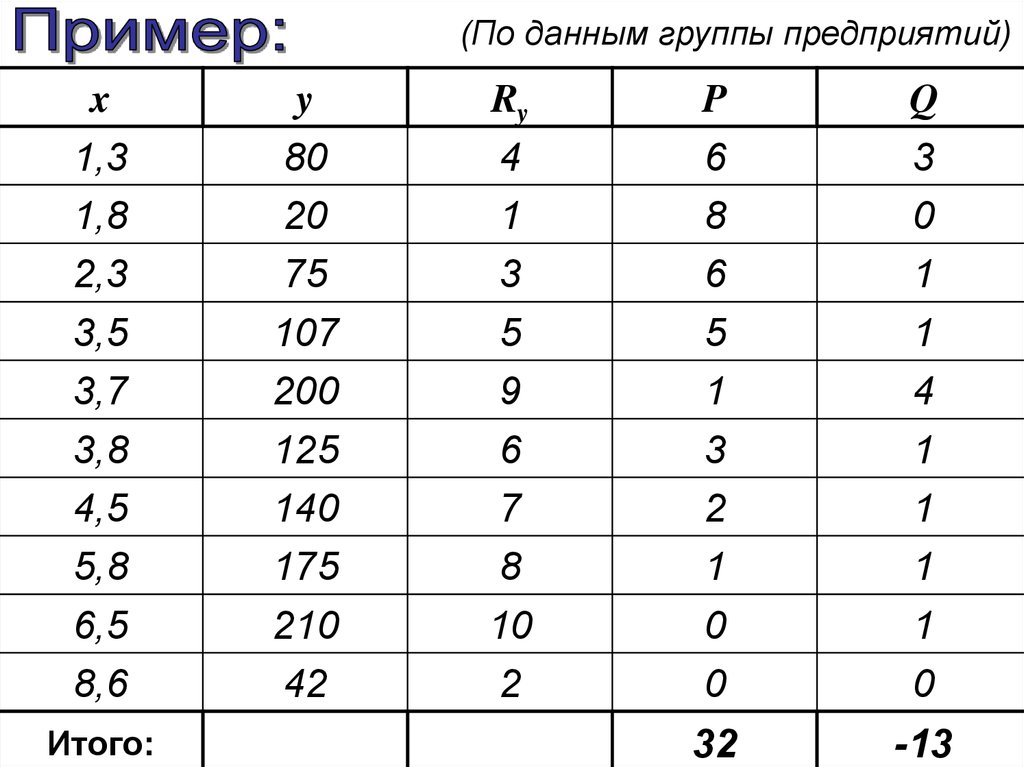
100.

(По данным группы предприятий)
x
1,3
1,8
2,3
3,5
3,7
3,8
4,5
5,8
6,5
8,6
Итого:
y
80
20
75
107
200
125
140
175
210
42
Ry
4
1
3
5
9
6
7
8
10
2
P
6
8
6
5
1
3
2
1
0
0
Q
3
0
1
1
4
1
1
1
1
0
32
-13

101.

xy
2( 32 13)
0,42
10(10 1)
Связь близка к умеренной

102.

0,5
0,5
xy
2
3
xy
Связь
статистически
значима
Как правило
При достаточно
больших объемах
совокупности

103.

12 S
W
2
3
m ( n n)
m – количество факторов
n – число наблюдений
S – отклонение суммы квадратов рангов
от средней квадратов рангов

104.

Значимость коэффициента конкордации
проверяется
2
на основе
-критерия Пирсона
2
12 S
m n( n 1)

105.

Собстве
Стоимость Кредитные
нный
активов,
вложения,
Сумма
Банк
капитал, Ry Rx1 Rx2
млн.руб.
млн.руб.
строк
млн.руб.
(y)
(x1)
(x2)
Квад
раты
сумм
1
3176
2496
209
7
7
7
21
441
2
3066
1962
201
6
6
6
18
324
3
2941
783
177
5
3
5
13
169
4
1997
1319
136
4
5
4
12
144
5
1865
1142
175
3
4
3
11
121
6
1194
658
88
2
2
2
6
36
7
518
311
60
1
1
1
3
9
84
1244
Итог

106.

84 2
S 1244
236
7
12 236
W 2 3
0,94
3 (7 7)
12 236
22,5
3 7(7 1)
2
22,5 12,596
2
2
k
( 0,05; n 1 7 1 6)
По таблице
«распределение Пирсона»
( 2 -распределение)
Коэффициент конкордации значим,
связь между признаками сильная