Статистические методы изучения взаимосвязей в судебной статистике

1.

РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПРАВОСУДИЯ
КРЫМСКИЙ ФИЛИАЛ
кафедра уголовно-процессуального права
Учебно-наглядное пособие
Дисциплина: Судебная статистика
Тема №10
«Статистические методы изучения взаимосвязей в судебной статистике»
Подготовил:
доцент кафедры,
кандидат юридических наук
И.В. Романовская
Симферополь
2025

2. Тема № 10 «Статистические методы изучения взаимосвязей в судебной статистике»

План лекции:
Введение
1. Основные понятия о статистической взаимосвязи. Виды
статистических взаимосвязей.
2. Методы выявления статистических связей.
Заключение (выводы)

3. Вопрос 1. Основные понятия о статистической взаимосвязи. Виды статистических взаимосвязей

Важной частью анализа статистических данных является изучение связей
между явлениями.
Оценка наиболее существенных причинно-следственных связей между
количественными характеристиками явлений, а также воздействия одних
факторов на другие является одной из основных задач статистики.
Формы проявления взаимосвязей весьма разнообразны. В качестве двух
самых общих их видов выделяют функциональную (полную) и
корреляционную (неполную) связи.
При функциональной связи величине факторного признака строго
соответствует одно или несколько значений функции (результативного
признака). Это связь строгая, ее можно рассчитать по формуле.

4. Вопрос 1. Основные понятия о статистической взаимосвязи. Виды статистических взаимосвязей

Корреляция — мера согласованности одного признака с одним или с
несколькими признаками, либо взаимная согласованность группы признаков.
Корреляция (корреляционная зависимость) — величина, характеризующая
взаимную зависимость двух случайных величин, или которых можно считать
таковыми, используется для выявления вероятностной или статистической
зависимости величин при обработке данных.
Математической мерой корреляции двух случайных величин служит коэффициент
корреляции, который измеряется от –1 до +1, показывая прямую (положительную) или
обратную (отрицательную) зависимость случайных величин. Если значение по
модулю находится ближе к 1, то это означает наличие сильной связи, а если ближе к 0
— связь слабая или вообще отсутствует. При коэффициенте корреляции, равном по
модулю единице, говорят о функциональной связи, то есть изменения двух величин
можно описать математической функцией.

5. Вопрос 1. Основные понятия о статистической взаимосвязи. Виды статистических взаимосвязей

Прямые
и
обратные
связи
различаются
от
направления
изменения
результативного признака.
Если факторный признак растет, то растет и результативный. Это связь прямая
(чем дольше лица трудоспособного возраста не имеют определенных законных
занятий, тем чаще такие лица совершают преступления против собственности).
Если факторный признак растет, а результативный снижается, то это связь
обратная (чем выше возраст привлеченных к уголовной ответственности, тем ниже
среди них доля лиц, совершивших преступления, связанные с незаконным
оборотом
наркотиков).
Такие
связи
положительными и отрицательными.
также
называют
соответственно

6. Вопрос 1. Основные понятия о статистической взаимосвязи. Виды статистических взаимосвязей

Относительно
своей
аналитической
формы
связи
бывают
линейными и нелинейными. В первом случае между признаками в
среднем проявляются линейные соотношения. Нелинейная взаимосвязь
выражается нелинейной функцией, а переменные связаны между собой в
среднем нелинейно.
По характеру взаимодействующих факторов различают парную
связь, характеризуют связь двух признаков, если изучаются более двух
взаимодействующих признаков — множественной.

7. Вопрос 1. Основные понятия о статистической взаимосвязи. Виды статистических взаимосвязей

Однофакторная связь — связь между одним факторным и одним результативным
признаком (частная или парная корреляция).
Многофакторная связь — связь между несколькими факторными и одним результативным
признаком (множественная корреляция).
Применение корреляционного анализа возможно при достаточном объеме единиц
наблюдений, которые должны превышать на порядок число факторов, при однородности
изучаемой совокупности. Однако следует иметь в виду, что наличие корреляционной связи не
даёт основания утверждать, что один из факторов является причиной другого, а не
имеется действие иного фактора.
Прямолинейные и криволинейные связи различаются в зависимости от функции, которой
они могут быть приблизительно описаны — линейной (прямолинейная связь) или
криволинейной — параболы, гиперболы, полулогарифмической кривой, показательной кривой
(криволинейная связь).

8. Вопрос 1. Основные понятия о статистической взаимосвязи. Виды статистических взаимосвязей

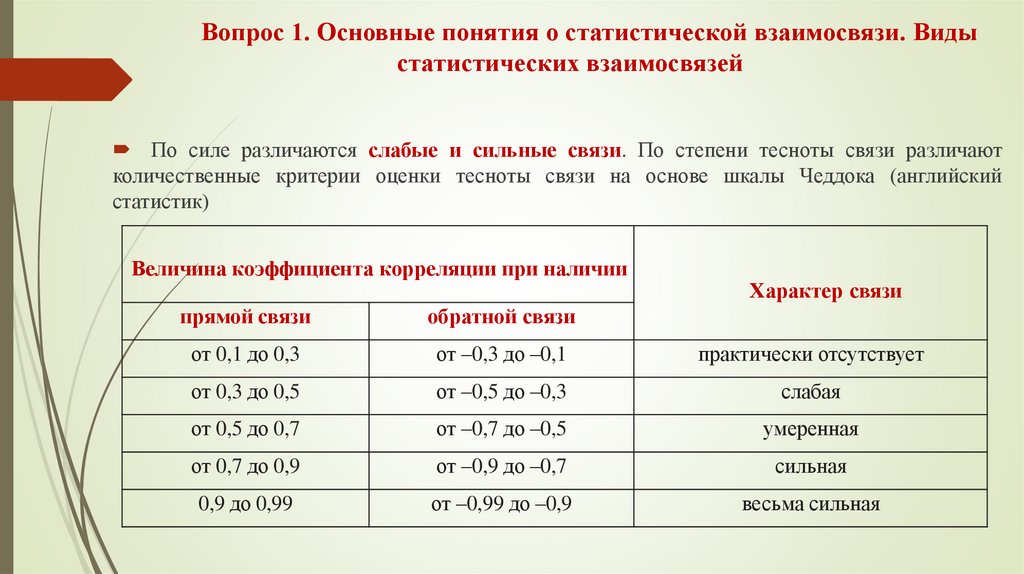
По силе различаются слабые и сильные связи. По степени тесноты связи различают
количественные критерии оценки тесноты связи на основе шкалы Чеддока (английский
статистик)
Величина коэффициента корреляции при наличии
Характер связи
прямой связи
обратной связи
от 0,1 до 0,3
от –0,3 до –0,1
практически отсутствует
от 0,3 до 0,5
от –0,5 до –0,3
слабая
от 0,5 до 0,7
от –0,7 до –0,5
умеренная
от 0,7 до 0,9
от –0,9 до –0,7
сильная
0,9 до 0,99
от –0,99 до –0,9
весьма сильная

9. Вопрос 1. Основные понятия о статистической взаимосвязи. Виды статистических взаимосвязей

Задача статистики в области изучения взаимосвязей состоит в количественной оценке их
наличия и направления, а также характеристике силы и формы влияния одних факторов на
другие. Для ее решения применяются методы корреляционно-регрессионного анализа.
Задачи корреляционного анализа — измерение тесноты связи между варьирующими
признаками, определение неизвестных причинных связей и оценка факторов, оказывающих
наибольшее влияние на результативный признак.
Задачи регрессионного анализа — установление формы зависимости, определение
функции регрессии, использование уравнения для оценки неизвестных значений зависимой
переменной.
Регрессия — это линия, характеризующая наиболее общую тенденцию во взаимосвязи
факторного и результативного признаков. Предполагается, что аналитическое уравнение
выражает подлинную форму зависимости, а все отклонения от этой функции обусловлены
действием различных случайных причин. Так как изучаются корреляционные связи, изменению
факторного признака соответствует изменение среднего уровня результативного признака.

10. Вопрос 1. Основные понятия о статистической взаимосвязи. Виды статистических взаимосвязей

Выводы:
Для выявления наличия связи, ее характера и направления применяются
различные статистические методы. Поскольку зависимости в статистике
проявляются через вариацию признаков, то и методы в основном измеряют и
сопоставляют вариацию факторного и результативного признаков.
Для исследования статистических связей используется специальное
программное обеспечение (статистические пакеты), однако для их использования
надо уметь подготовить статистические данные, понимать смысл выполняемых
автоматизированно расчетов и уметь интерпретировать полученные результаты.
Заключение о связи признаков можно получить графическим (зрительным) и
расчётным (аналитическим) путём.

11. Вопрос 2. Методы выявления статистических связей

Выявление корреляционной связи осуществляется методами, которые делят на две группы:
Нематематические:
метод параллельных
рядов
метод аналитических
группировок
графический метод
Математические:
регрессионный
корреляционный
Дают приближенную оценку наличия
Примеры для установления связей
формы и направлении связи
параллельное сопоставление рядов Соотношение
уровней
мелких
значений факторного и результативного хищений и краж по субъектам РФ
признаков;
построение
групповой
и Выбор подсудимыми рассмотрения
корреляционной таблиц, факторные дела судом с участием присяжных
аналитические
группировки, заседателей в зависимости от
исчисление групповых средних;
вынесения
судом
присяжных
оправдательных
приговоров
графическое изображение фактических
(соотношение долей по субъектам
данных с помощью поля корреляции.
РФ)
Заключаются в нахождении уравнения
связи, где результативный признак зависит
только от интересующего фактора (или
нескольких факторов), а все прочие
факторы, также влияющие на результат,
принимаются за постоянные средние.

12. Вопрос 2. Методы выявления статистических связей

При отсутствии ярко выраженной причинной связи между факторным и результативным признаками наличие и
характер связи можно установить при помощи метода параллельных рядов: в одной таблице приводятся
упорядоченные значения факторного признака, который обычно обозначается символом х, и соответствующие им
значения результативного признака, который обычно обозначается символом Y. Метод параллельных рядов обычно
используется для установления характера связи при относительно небольшом объеме исходных данных: применяется
для определения наличия и направления взаимосвязи при немногочисленных совокупностях (15–20 единиц).
Суть метода сравнения параллельных рядов состоит в том, что полученные в результате группировки и счетной
обработки материалы статистического наблюдения располагаются ранжированными по факторному признаку
параллельными рядами. Параллельно записываются значения результативного признака. Это дает возможность,
сравнивая значения факторных и результативных показателей, проследить соотношения, выявить наличие связи и ее
направление. При этом методе значение факторного признака располагается в порядке возрастания или
убывания и параллельно с ними отражаются соответствующие значения результативного признака. Сопоставляя
ряды значений, устанавливается зависимость. Данный метод позволяет вывести только направление связи, но не
измерить ее.
В тех случаях, когда возрастание величины факторного признака влечет за собой возрастание величины
результативного признака, говорят о возможном наличии прямой корреляционной связи.
Если же с увеличением факторного признака величина результативного признака имеет тенденцию к уменьшению,
то можно предполагать обратную связь между этими признаками. Например, параллельное сопоставление рядов
индивидуальных значений (стаж судьи и число изменений, вносимых в судебные акты вышестоящим судом) показывает
на наличие обратной корреляционной связи.

13. Вопрос 2. Методы выявления статистических связей

Графический метод заключается в построении корреляционного поля —
значения факторного признака отражаются на оси Х, результативного
(определяемый им, зависимый) — ось ординат (Y).
По корреляционному полю также можно судить о характере взаимосвязи.
Если точки сконцентрированы около диагонали, идущей слева направо,
снизу вверх — то связь прямая.
Если около другой диагонали — обратная.
Если точки рассеяны по всему полю графика — связь отсутствует.
Взаимосвязь признаков отображается в MS Excel точечной диаграммой.

14. Вопрос 2. Методы выявления статистических связей

Однако при наличии большого числа значений признаков, когда одному и тому же значению
признака-фактора, как правило, соответствует несколько различных значений результативного
признака, восприятие параллельных рядов сильно затрудняется. В этих случаях целесообразно
для установления наличия связи воспользоваться методом построения корреляционных
таблиц.
Построение корреляционной таблицы начинают с группировки значений факторного и
результативного признаков. В корреляционной таблице, как правило, в подлежащем
указывается факторный признак х, а в сказуемом — результативный признак у.
В корреляционной таблице указываются частоты: сколько раз данная величина одного
признака повторяется в сочетании с соответствующей величиной другого признака. Итоговые
графа и строка отражают распределение единиц совокупности по рассматриваемым признакам.
Если частоты в корреляционной таблице расположены на «главной» диагонали (из левого
верхнего угла в правый нижний угол), но можно предположить наличие прямой
корреляционной зависимости между признаками.
Если же частоты расположены по «вспомогательной» диагонали (из левого нижнего угла в
правый верхний угол), то предполагают наличие обратной связи между признаками.
Если количество исследуемых единиц значительно, а значения признаков не совпадают,
корреляционная таблица будет объемная и оценка закономерности будет затруднена. В этом
случае целесообразно сгруппировать значения признаков по строкам и графам по равным
интервалам, найти их среднее значение и составить сгруппированную корреляционную таблицу,
где в графоклетке будет указано количество единиц, попадающих в диапазон, соответствующих
средних значений.

15. Вопрос 2. Методы выявления статистических связей

Метод составления корреляционной таблицы и метод параллельных
рядов базируются на сопоставлении индивидуальных значений изучаемых
признаков.
А индивидуальные значения формируются под влиянием как основных,
так и случайных факторов.
Корреляционная связь обнаруживается более четко, если влияние
случайных
факторов
применении
для
удается
выявления
нивелировать.
наличия
Это
обеспечивается
корреляционной
связи
аналитической группировки и исчисления групповых средних.
при
метода

16. Вопрос 2. Методы выявления статистических связей

Метод аналитической группировки применяется в случаях, когда
совокупность достаточно велика и параллельные ряды не позволяют
обнаружить зависимость (от 100 единиц). Состоит в следующем:
совокупность результатов наблюдений разбивается на группы по величине
факторного признака и для каждой группы вычисляется средняя величина или
относительная величина результативного признака.
При этом необходимо образовать такое количество групп, чтобы
групповые средние перестали носить случайный характер и с каждой новой
группой имели тенденцию к росту или снижению. Изменения средних или
относительных значений результативного признака сопоставляются с
изменениями факторного признака для выявления характера связи между
ними.
Результаты аналитической группировки представляют в виде итоговой
статистической таблицы. При построении аналитической группировки важно
правильно определить величину интервала.

17. Вопрос 2. Методы выявления статистических связей

Более глубокий анализ осуществляется с помощью математических методов —
регрессионного и корреляционного анализа (общее понятие корреляционнорегрессионный анализ).
Корреляционный анализ имеет своей задачей количественное определение тесноты
и направления связи между двумя признаками (при парной связи) и между
результативным и множеством факторных признаков (при многофакторной связи).
Теснота связи количественно выражается величиной коэффициентов корреляции,
которые, давая количественную характеристику тесноты связи между признаками,
позволяют определить корректность использования факторных признаков при
построении уравнения множественной регрессии. Знаки при коэффициентах корреляции
характеризуют направление связи между признаками.
После выявления с помощью корреляционного анализа наличия статистических
связей между переменными и оценки тесноты связи переходят к математическому
(аналитическому) описанию зависимостей с использованием регрессионного анализа.
Подбирается класс функций, связывающий результативный показатель (у) и факторные
(аргументы функции х). Функция, описывающая зависимость среднего значения
результативного признака у от заданных значений аргументов, называется функцией
(уравнением) регрессии. Вид уравнения регрессии выбирают исходя из сущности явления
и результатов наблюдений.

18. Вопрос 2. Методы выявления статистических связей

Регрессионный анализ позволяет выразить с помощью уравнения форму
взаимосвязи, т. е. исследует аналитическое выражение взаимосвязи между
признаками, в котором изменение среднего значения результативного признака
обусловлено влиянием одного или нескольких факторов, множество других
факторов, оказывающих влияние на результативный признак, принимается за
постоянные или средние уровни.
Одной из проблем построения уравнений регрессии является их
размерность, то есть определение числа факторных признаков, включаемых в
модель. Их число должно быть оптимальным.
Сокращение размерности за счет исключения второстепенных,
несущественных факторов позволяет получить модель взаимосвязи.
Наиболее
используемым
методом
построения
математических
зависимостей является метод наименьших квадратов (МНК).

19. Вопрос 2. Методы выявления статистических связей

Метод
наименьших
применяемый
для
квадратов
решения
—
различных
математический
задач,
метод,
основанный
на
минимизации суммы квадратов отклонений некоторых функций от
искомых переменных, один из базовых методов регрессионного анализа
для
оценки
неизвестных
выборочным данным.
параметров
регрессионных
моделей
по

20. Вопрос 2. Методы выявления статистических связей

Математические методы установления взаимосвязей делятся на:
Параметрические
→ дают оценку тесноты связи
Применяются для измерения
непосредственно на базе значений
связи признаков по их значениям
факторного и результативного
признаков.
Непараметрические → дают оценку на основе условных Применяются как отдельно, так и
оценок признаков. Их еще
совместно с параметрическими.
называют ранговыми методами. Они
Особенно эффективны, когда
связаны с расчетами различных
необходимо измерить связь
коэффициентов: коэффициент
между качественными
Фехнера (коэффициент совпадения
признаками. Они проще в
знаков), коэффициенты ассоциации и вычислении и не требуют никаких
контингенции, коэффициент
предположений о законе
Спирмена (ранговый коэффициент).
распределения исходных
статистических данных, т. к. при
их расчете оперируют не самими
значениями признаков, а их
рангами, частотами, знаками и т. д.

21. Вопрос 2. Методы выявления статистических связей

Если анализируется зависимость одного факторного и результативного
признаков, то в этом случае имеем дело с парной корреляцией и парной
регрессией. Если анализируются несколько факторных и результативных
признаков — это множественная корреляция и регрессия.
Рассмотрим для примера три метода оценки взаимосвязи:
коэффициент Фехнера,
линейный коэффициент корреляции,
коэффициент ранговой корреляции Спирмена.

22. Вопрос 2. Методы выявления статистических связей

Коэффициент Фехнера, основанный на определении корреляции знаков,
представляется наиболее простым показателем связи.
Расчет коэффициента Фехнера основан на оценке степени согласованности
направлений отклонений индивидуальных значений факторного и результативного
признаков от соответствующих средних — на совпадении знаков «плюс» и «минус» у
двух признаков.
Вычисляют средние значения результативного и факторного признаков, а затем
проставляют знаки отклонений для всех значений взаимосвязанных пар признаков. Знаки
вычисляются как результат разности индивидуальных значений каждого признака
исследуемых единиц и среднего значения (отклонение от среднего значения).
Подсчитывается число совпадений и несовпадений.
Коэффициент Фехнера может принимать различные значения в пределах от –1
до +1.
Если знаки всех отклонений совпадут, коэффициент будет равен +1, что
свидетельствует о возможном наличии прямой связи.
Если же знаки всех отклонений будут разными, коэффициент Фехнера будет равен –1,
что дает основание предположить наличие обратной связи.

23. Вопрос 2. Методы выявления статистических связей

Линейный коэффициент корреляции — параметрический метод, наиболее
совершенно характеризует тесноту связи. Предложен в конце ХIХ в. Пирсоном.
C H
Kô
,
C + H
где C — число совпадений знаков, H — число несовпадений,
C + H — число исследуемых единиц.
Линейный коэффициент корреляции может быть положительным или
отрицательным.
Положительная его величина свидетельствует о прямой связи, отрицательная
— об обратной. Чем ближе величина к ±1, тем связь теснее.
При функциональной связи между признаками значение будет равно ±1.
Близость к 0 означает, что связь между признаками слабая.

24. Вопрос 2. Методы выявления статистических связей

Коэффициент корреляции рангов — непараметрический метод, оценивает
силу связи.
Коэффициент
учитывает
согласованность
рангов,
соответствующих
отдельным единицам совокупности по каждому из двух исследуемых признаков.
Ранги — это порядковые номера единиц совокупности в ранжированном ряду.
Совокупность ранжируется по факторному признаку в порядке возрастания и
единицам совокупности присваиваются соответствующие ранги. Параллельно
проставляются ранги тех же единиц совокупности, какие они заняли бы в
ранжированном ряду по результативному признаку.

25. Вопрос 2. Методы выявления статистических связей

Метод ранговой корреляции Спирмена позволяет определить тесноту (силу) и
направление корреляционной связи между двумя признаками или двумя
иерархиями признаков.
Для подсчета ранговой корреляции Спирмена необходимо располагать двумя
рядами значений, которые могут быть проранжированы. Такими рядами значений
могут быть два признака, измеренные в одной и той же совокупности (выборочной
совокупности).
Ограничения применения коэффициента ранговой корреляции:
по каждой переменной должно быть представлено не менее 5 наблюдений;
коэффициент ранговой корреляции Спирмена при большом количестве
одинаковых рангов по одной или обеим сопоставляемым переменным дает
огрубленные значения. В идеале оба коррелируемых ряда должны
представлять собой две последовательности несовпадающих значений.

26. Вопрос 2. Методы выявления статистических связей

Коэффициент ранговой корреляции может принимать значения в
пределах: — 1 ≤ ρ ≤ 1.
Когда ранги факторного признака полностью совпадают с рангами
результативного признака, тогда имеет место почти прямая связь между
признаками и ρ=1.
Если ранги расположились строго в противоположном направлении, то
наблюдается полная обратная корреляция рангов и ρ = — 1.
При ρ = 0 корреляция рангов отсутствует.
Необходимо иметь в виду, что когда эмпирический показатель принимает
крайние значения ±1 или 0, то это не означает, что существует функциональная
связь или зависимость абсолютно отсутствует. Во всех других случаях, когда
коэффициент ранговой корреляции не принимает крайних значений, он
интерпретируется так же, как и коэффициент линейной корреляции и обладает
такими же особенностями.

27. Вопрос 2. Методы выявления статистических связей

Выводы:
Рассмотрим применение различных методов установления взаимосвязи между явлениями на
примерах.
1. По данным сводной статистической отчетности по форме № 1-АП (число наказанных за
совершение мелкого хищения и форме № 11 (осуждено по ст. 158 УК РФ), детализированным по
субъектам Российской Федерации, проверяется наличие связи между привлечением к
административной ответственности за мелкое хищение и судимости за кражи.
2. Перед исследователем стоит задача изучить причины выбора подсудимыми рассмотрения дела с
участием присяжных заседателей. По областным и равным им судам доля дел, рассматриваемых с
участием присяжных заседателей, от общего числа оконченных производством дел варьируется от
100% до 0. Для анализа используются данные сводной статистической отчетности по форме № 1 за год
по областным и равным им судам, включая окружные (флотские) военные суды. Предполагаем, что
мотивом выбора суда с участием присяжных заседателей является число выносимых в конкретном суде
при рассмотрении дела с участием присяжных заседателей оправдательных приговоров. Причинами
вынесения оправдательных приговоров могут быть как проблемы с качеством следствия и подготовкой
обвинения, так и субъективными факторами, определяющими ведение процесса и формирование
позиции присяжных. Исследование различными методами параллельных рядов, графическим методом,
расчетом коэффициента парной ранговой корреляции позволяет сделать вывод о наличии умеренной
связи между практикой вынесения оправдательных приговоров и выбором подсудимыми рассмотрения
дела с участием присяжных заседателей.

28. Тема № 10 «Статистические методы изучения взаимосвязей в судебной статистике»

Для подготовки к семинарскому занятию студентам необходимо подготовиться к опросу по
следующим вопросам:
1. Основные понятия о статистической взаимосвязи функциональная (полная) и корреляционная
(неполная) связи. Прямые и обратные связи.
2. Виды статистических взаимосвязей. Парная связь. Однофакторная связь.
3. Многофакторная связь: линейная (прямолинейная связь), криволинейная связь (парабола, гипербола,
полулогарифмическая кривая, показательная); кривая (криволинейная связь).
4. Задачи корреляционного анализа. Задачи регрессионного анализа.
5. Методы выявления статистических связей: нематематические (метод параллельных рядов, метод
аналитических группировок, графический метод) и математические (регрессионный и корреляционный).
6. Взаимодействие судебной практики и судебной статистики. Понятие причин и условий преступности.
Задача статистического анализа причин преступности, личности преступника и мотивации преступного
поведения.
7. Взаимосвязь преступных проявлений с системой статистических показателей.
Для подготовки к занятию студентам необходимо подготовить доклады по следующим темам:
1. Моделирование и прогнозирование состояния преступности и судимости.
2. Тестирование качества моделей: тест Фишера, тест Стьюдента, тесты на нелинейность моделей,
тесты на Гетероскедастичность, тест на нормальное распределение остатков, тест на автокорреляцию,
RESET-тест, анализ мультиколлениарности.