L4Statisticheskoe_izuchenie_vzaimosvyazi

1. Методы анализа взаимосвязи в библиотечной статистики

Сущность, задачи и основные понятия
корреляционно-регрессивного анализа
2. Измерение степени тесноты и интенсивности
корреляционной связи
3. Понятие регрессионного уравнения и сущность МНК
4. Проверка качества регрессионного уравнения и его
параметров
1.

2. Сущность, задачи и основные понятия корреляционно-регрессивного анализа

3.

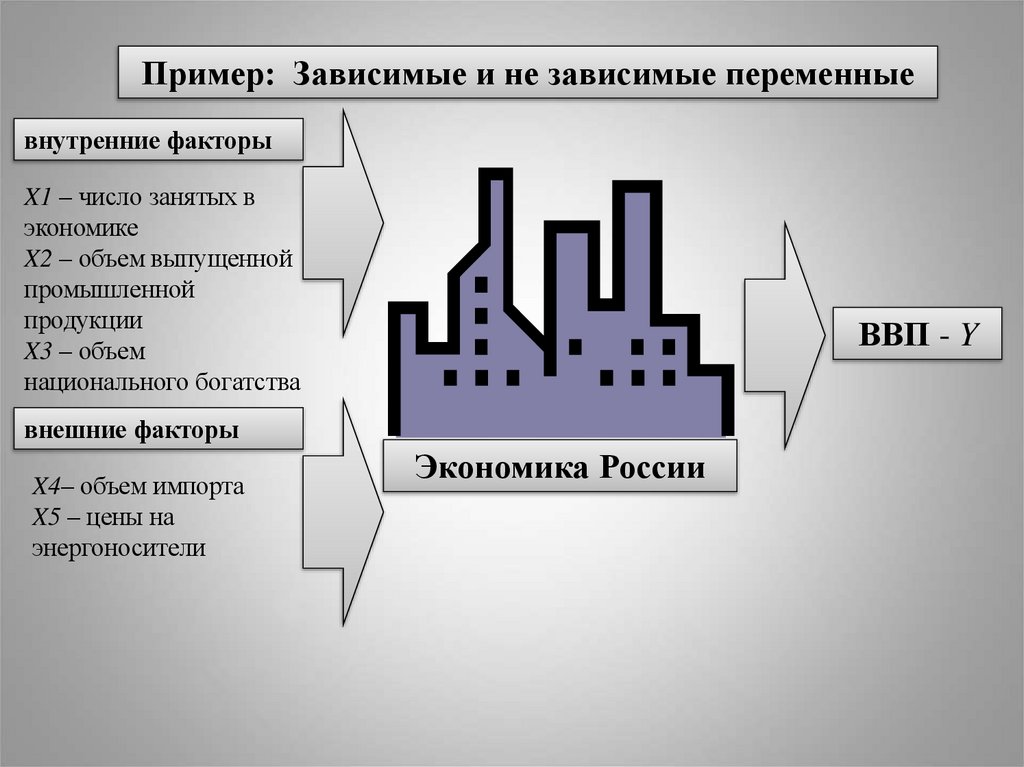
Пример: Зависимые и не зависимые переменные
внутренние факторы
X1 – число занятых в
экономике
X2 – объем выпущенной
промышленной
продукции
X3 – объем
национального богатства
ВВП - Y
внешние факторы
X4– объем импорта
X5 – цены на
энергоносители
Экономика России

4.

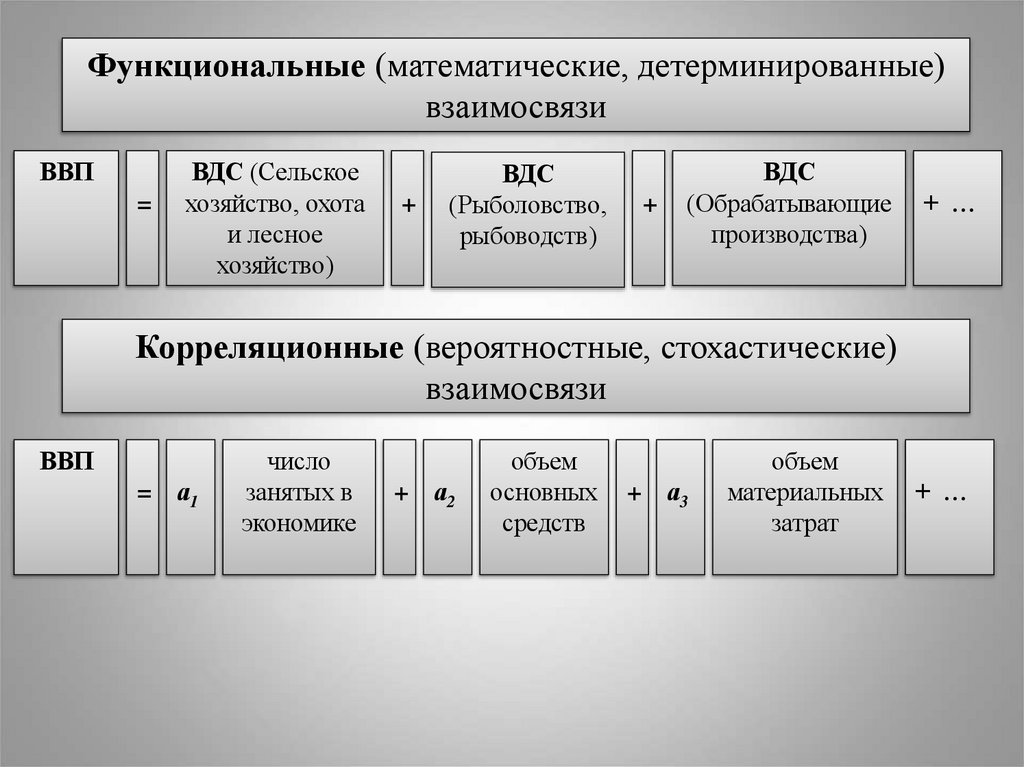
Функциональные (математические, детерминированные)
взаимосвязи
ВВП
=
ВДС (Сельское
хозяйство, охота
и лесное
хозяйство)
+
ВДС
(Рыболовство,
рыбоводств)
+
ВДС
(Обрабатывающие
производства)
+ …
Корреляционные (вероятностные, стохастические)
взаимосвязи
ВВП
= а1
число
занятых в
экономике
+ а2
объем
основных
средств
+ а3
объем
материальных
затрат
+ …

5. Задачи корреляционно-регрессионного анализа:

1. Выделение важных факторов, влияющих на
результативный признак, на базе мер тесноты связи
факторов с результативным признаком;
2. Описание влияния факторов посредством
регрессионного уравнения;
3. Оценка статистической значимости уравнения регрессии
и его параметров;
4. Прогнозирование (имитация) возможных значений
результативного признака при задаваемых значениях
факторных признаков.

6.

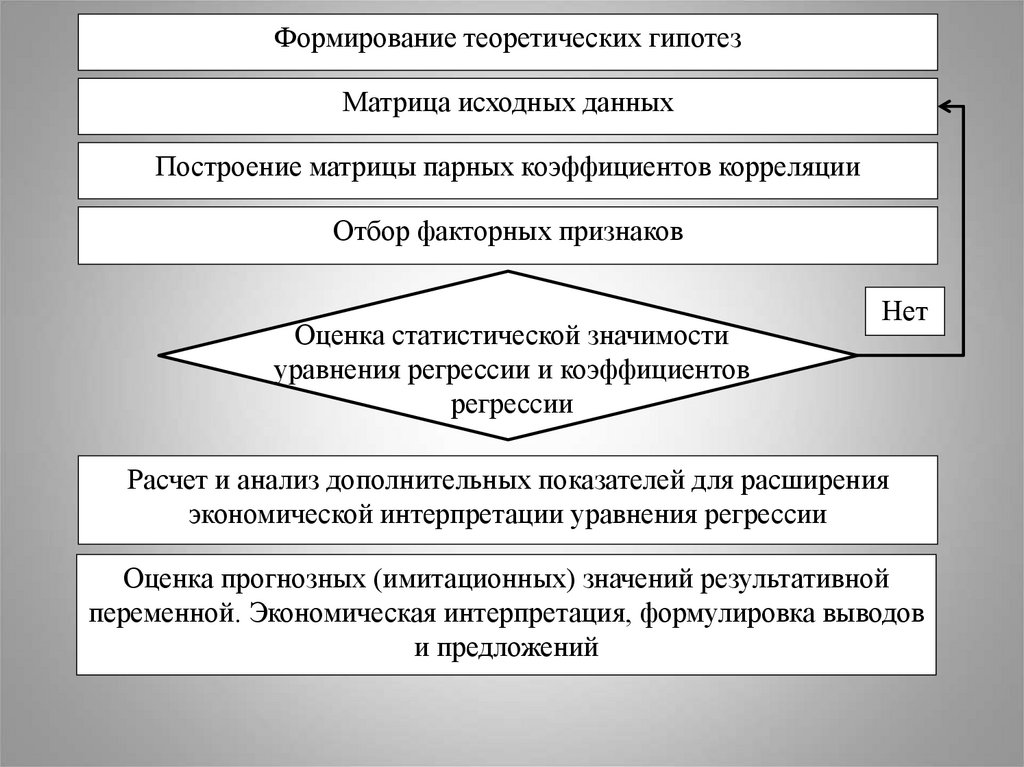
Формирование теоретических гипотез
Матрица исходных данных
Построение матрицы парных коэффициентов корреляции
Отбор факторных признаков
Оценка статистической значимости
уравнения регрессии и коэффициентов
регрессии
Нет
Расчет и анализ дополнительных показателей для расширения
экономической интерпретации уравнения регрессии
Оценка прогнозных (имитационных) значений результативной
переменной. Экономическая интерпретация, формулировка выводов
и предложений

7. Измерение степени тесноты и интенсивности корреляционной связи

8.

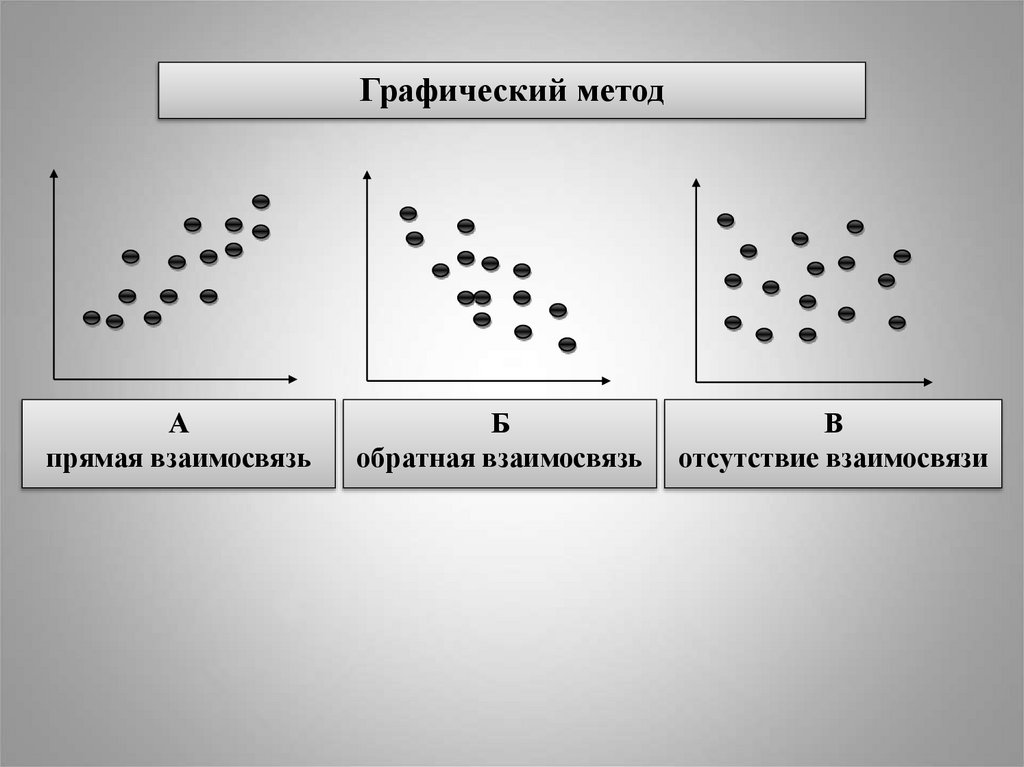
Графический метод
А
прямая взаимосвязь
Б
обратная взаимосвязь
В
отсутствие взаимосвязи

9. В статистике различают следующие варианты зависимостей:

1. парная корреляция – связь между двумя признаками, один
из которых результативный, а другой факторный;
2. частная корреляция – зависимость между результативным
и одним факторным признаком, при фиксированном
значении других факторных признаков;
3. множественная корреляция - зависимость результативного
признака от нескольких факторных признаков.
4. каноническая корреляция – зависимость группы
результативного признака от группы факторных признаков.

10.

Взаимосвязь между количественным варьирующим
признаками
Парный линейный коэффициент корреляции К.Пирсона
Принимает значения на отрезке [-1;1]
0 – связь между x и y отсутствует;
(0-0,3] - связь присутствует но она незначительна;
(0,3-0,5] - умеренная связь;
(0,5-0,7] - средняя связь;
(0,7-0,99] - тесная связь;
1 - связь между x и y функциональная.

11.

Частная линейная корреляция
в случае двух
независимых
переменных

12. Для применения частного коэффициента корреляции необходимо соблюдать следующие условия:

1. Сравниваемые переменные должны быть
измерены в шкале интервалов или отношений
2. Предполагается, что все переменные имеют
нормальный закон распределения
3. Число варьирующих признаков в сравниваемых
переменных должно быть одинаковым
4. Для оценки уровня достоверности
корреляционного отношения Пирсона следует
пользоваться формулой (приведенной выше) и
таблицей критических значений для t-критерия
Стьюдента при k = n – 2.

13.

Множественная линейная корреляция и
детерминация
на основе матрицы
парных коэффициентов
корреляции
на основе парных
коэффициентов корреляции
и бета коэффициентов
’ – определитель
ryx - парный
матрицы парных
коэффициент
коэффициентов
корреляции
корреляции;
β - бета коэффициенты
– определитель
матрицы межфакторной
корреляции
на основе парных
коэффициентов
корреляции
yi - индивидуальное
значение результативного
признака
- выровненные значения
по уравнению регрессии
- среднее значение
результативного признака
- скорректированный коэффициент
множественной детерминации

14. Понятие регрессионного уравнения и сущность МНК

15.

Регрессия это функциональная зависимость между
объясняющими переменными и условным
математическим ожиданием (средним значением)
зависимой переменой, которая строится с целью
предсказания (прогноз) этого среднего значения при
фиксированных значениях первых (регрессоров).

16.

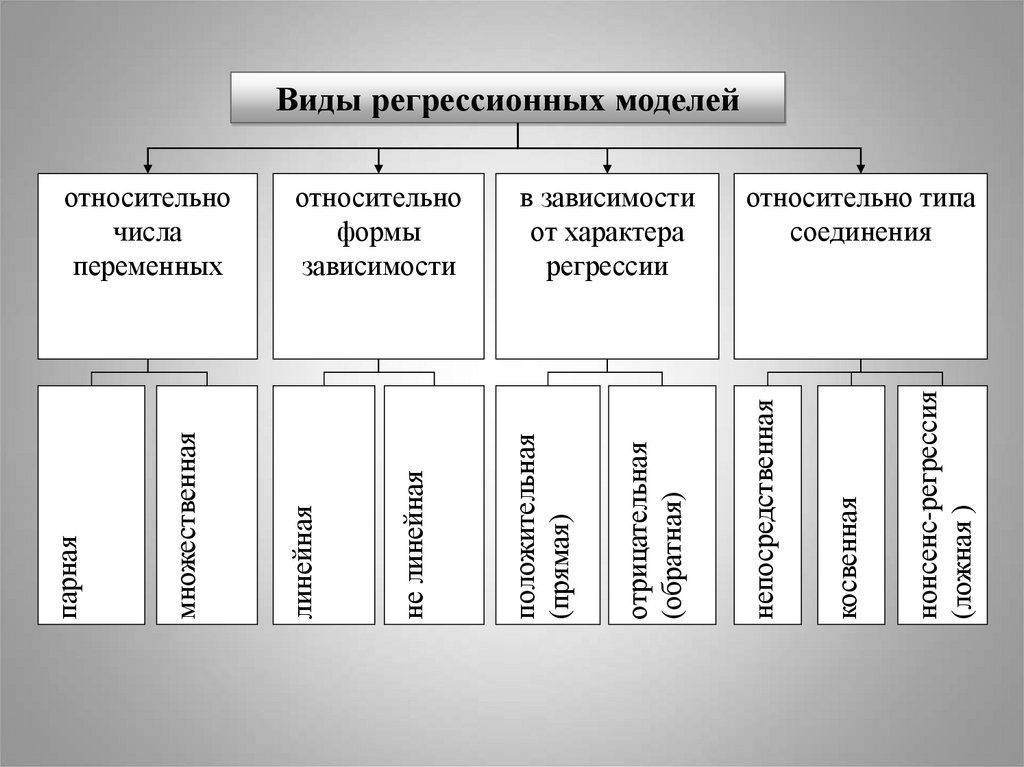
Виды регрессионных моделей
нонсенс-регрессия
(ложная )
косвенная
относительно типа
соединения
непосредственная
отрицательная
(обратная)
в зависимости
от характера
регрессии
положительная
(прямая)
не линейная
относительно
формы
зависимости
линейная
множественная
парная
относительно
числа
переменных

17. Выбор того или иного типа уравнения регрессии выполняется на основе следующих методик:

1. обоснование типа уравнения, исходя из
гипотез, полученных в ходе теоретических
разработок;
2. обоснование типа уравнения исходя из
вида графического изображения связи в
конкретной совокупности (только в случае
парной регрессии);
3. обоснование типа уравнения исходя из
величины показателей тесноты связи.

18. Множественная линейная регрессия

Парная линейная регрессия

19. При включении в уравнение регрессии необходимо руководствоваться следующими правилами:

факторы должны являться причинами, а
результативный показатель их следствием
факторы не должны быть составными частями
результативного показателя
не следует включать факторы, тесно связанных друг с
другом
рекомендуется использовать минимальное, но
достаточное количество факторов
факторы должны быть измерены количественно
следует включать факторы одного уровня иерархии
информация о факторах должна быть доступность,
достоверность и сопоставимой

20.

Название
Линейная
Параболическая
Гиперболическая
Показательная
Степенная
Функция

21.

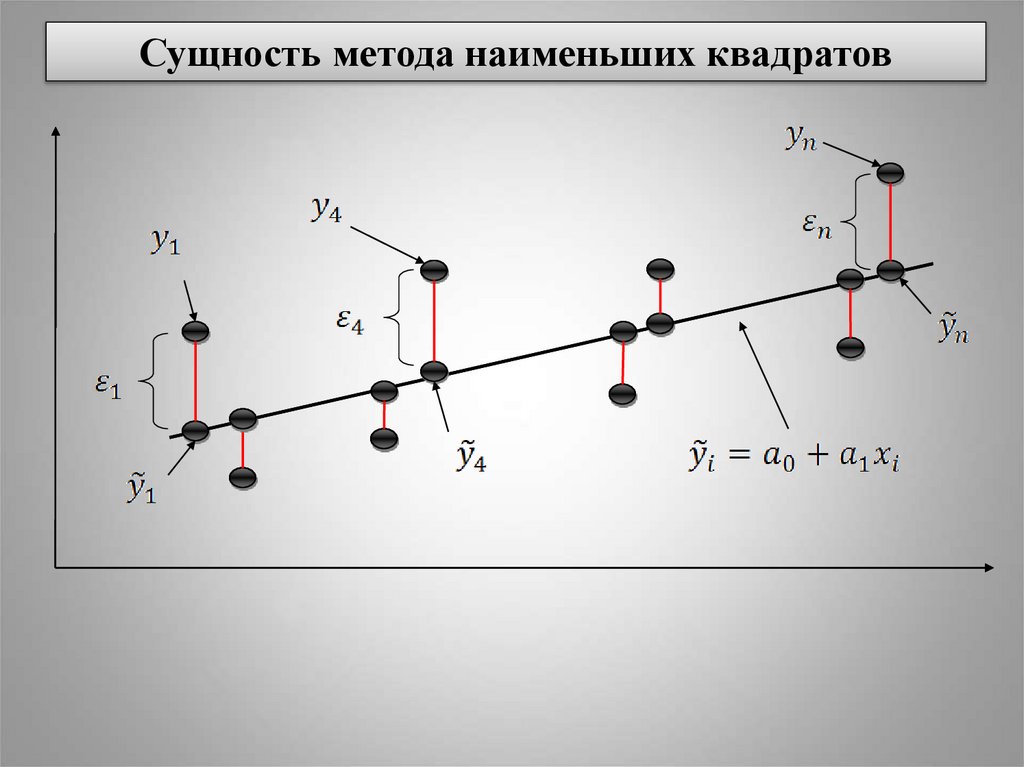
Сущность метода наименьших квадратов

22.

/n

23.

Параметры множественного уравнения регрессии можно
оценить используя:
табличные
редакторы
MS Excel
Lotus 1-2-3
Quattro Pro
StarOffice Calc
602Tab
эконометрические
пакеты программ
статистические
(общего назначения)
пакеты программ
Stata 8.0
Econometric
Vwise 5
Statistica 6.0
SPSS 10.0
StatGraphic
STADIA6.0

24.

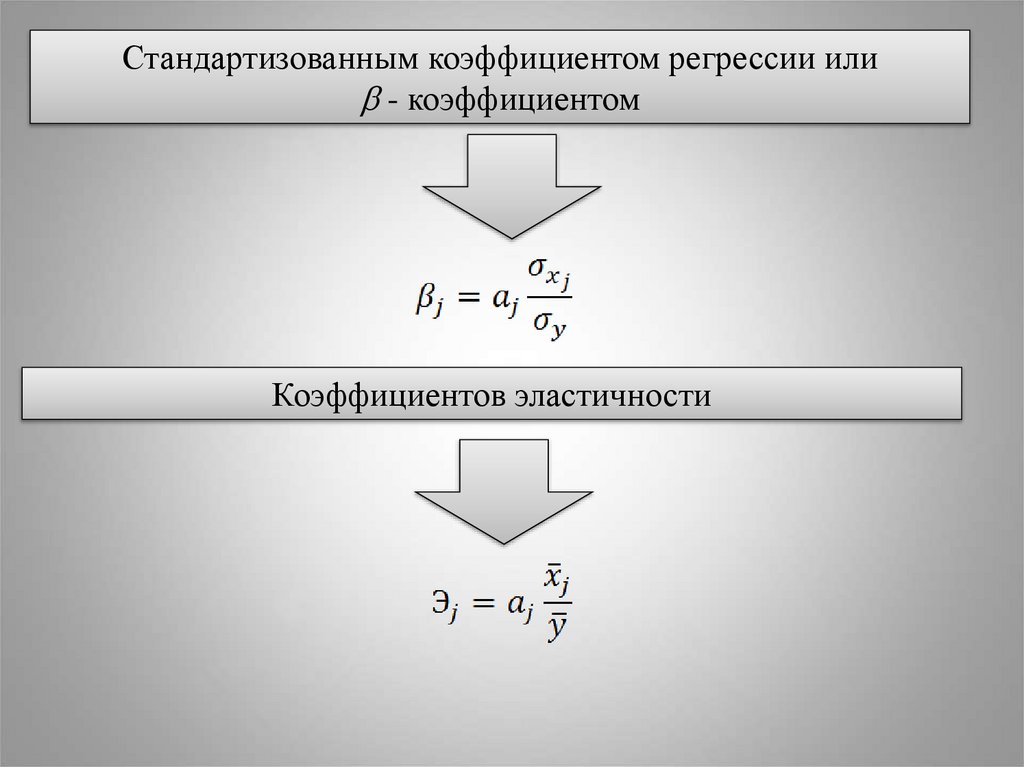
Стандартизованным коэффициентом регрессии или
- коэффициентом
Коэффициентов эластичности

25. Проверка качества регрессионного уравнения и его параметров

26.

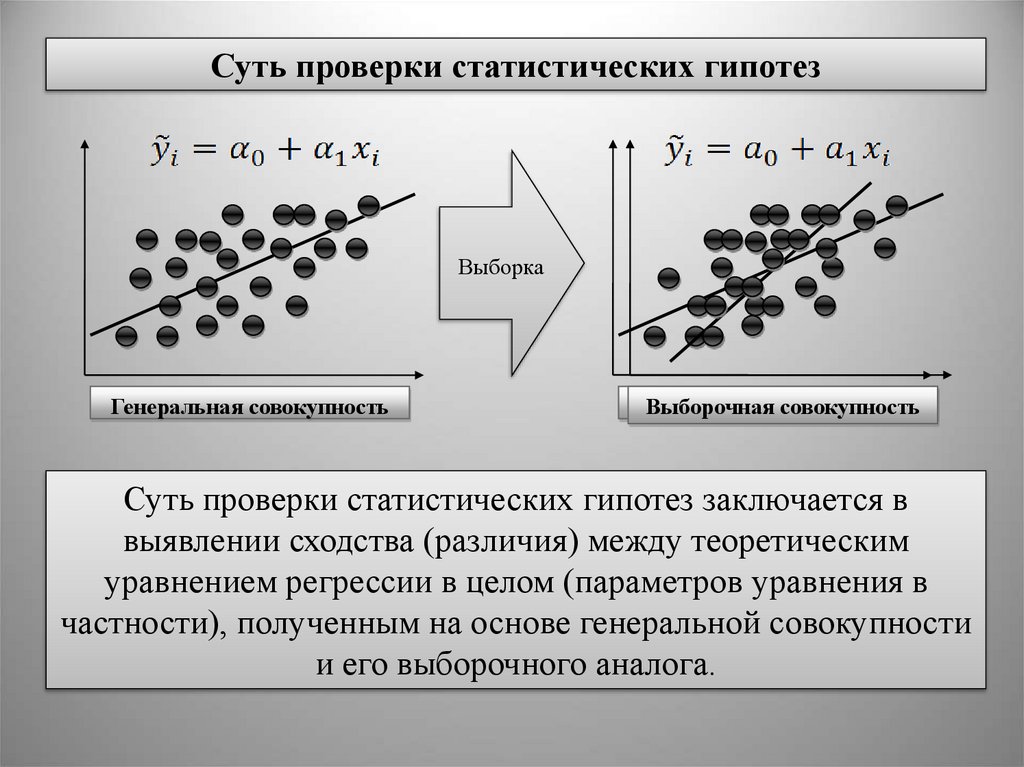
Суть проверки статистических гипотез
Выборка
Генеральная совокупность
Выборочная
Выборочнаясовокупность
совокупность
Суть проверки статистических гипотез заключается в
выявлении сходства (различия) между теоретическим
уравнением регрессии в целом (параметров уравнения в
частности), полученным на основе генеральной совокупности
и его выборочного аналога.

27.

H0 - нулевая гипотеза
Н1 – альтернативная гипотеза
Ошибка первого рода произойдет, когда будет принято решение
отклонить гипотезу H0, хотя в действительности она оказывается верной.
Ошибка второго рода произойдет, когда будет принято решение не
отклонять гипотезу H0 хотя в действительности она будет неверна.
Возможные состояния проверяемой гипотезы
Результат проверки
Верна гипотеза H0
Верна гипотеза H1
Гипотеза H0
Ошибка первого рода
Правильно, решение
Гипотеза H0 не
отклоняется
Правильное решение
Ошибка второго рода

28. Правило принятия статистического вывода таково:

1. на основании полученных экспериментальных данных
аналитик подсчитывает по выбранному им
статистическому методу, так называемую эмпирическую
статистику (фактическая или расчетная)
2. эмпирическая статистика (или критерий) сравнивается с
двумя критическими величинами (табличными), которые
соответствуют уровням значимости в 5% и в 1%
3. сравнивают эмпирическое значение с двумя найденными
по таблицам критическими значениями

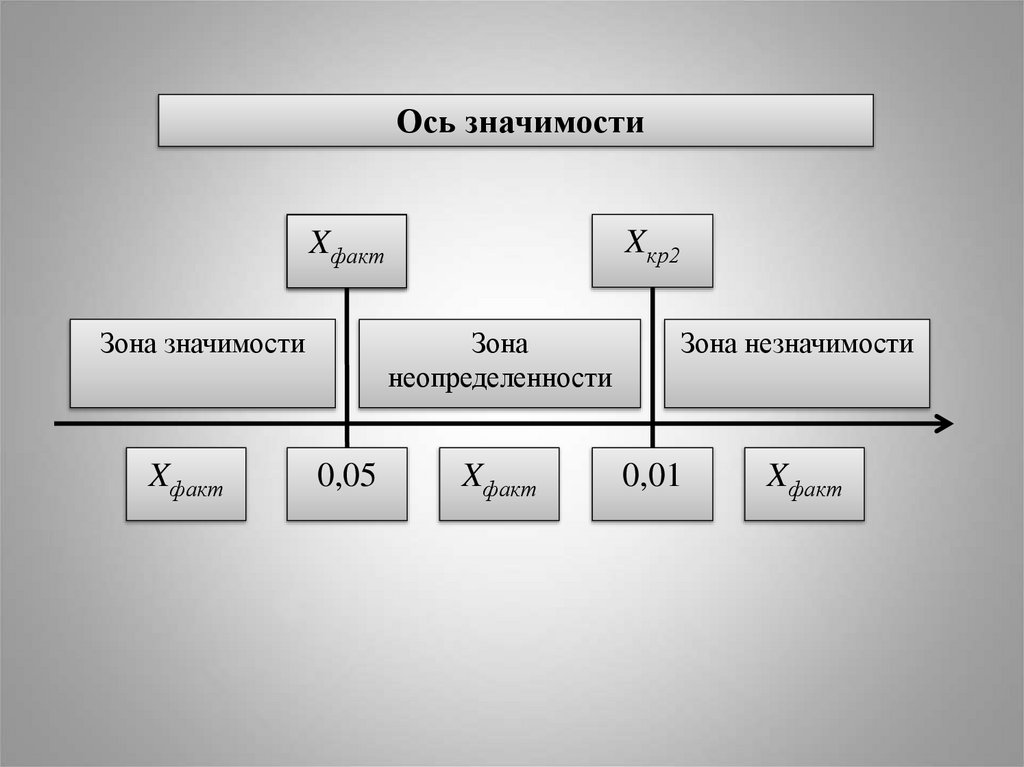
29.

Ось значимости
XXфакт
кр1
Зона значимости
Xфакт
Xкр2
Зона
неопределенности
0,05
Xфакт
Зона незначимости
0,01
Xфакт

30. Возможны четыре случая

1. Xфакт попало в зону незначимости - принимается гипотеза H0
об отсутствии различий
2. Xфакт попало в зону значимости - принимается альтернативная
гипотеза H1, о наличии различии, а гипотеза H0 отклоняется
3. Xфакт попало в зону неопределеннойсти - в зависимости от
важности решаемом задачи можно считать статистическую
оценку достоверной на уровне 5% и принять тем самым
гипотезу H1, отклонив гипотезу Н0 либо - недостоверной на
уровне 1% приняв тем самым гипотезу Н0
4. Xфакт может точно совпасть либо с Xкр1 либо с Xкр2 - В первом
случае можно считать, что оценка достоверна только на
уровне 5% и принять гипотезу H1 или напротив принять
гипотезу H0. Во втором случае, как правило, принимается
альтернативная гипотеза H1 о наличии различии, а гипотеза
H0 отклоняется

31. Алгоритм построения t-критерия Стьюдента:

1. шаг. Выдвигается H0 о равенстве нулю параметра
регрессионной модели.
2. шаг. Вычисляются стандартные ошибки параметров модели.
3. шаг. Рассчитывают фактическое (расчетное) значение tкритерия, для этого значение параметра регрессионного
уравнения делят на его стандартную ошибку.
4. шаг. По таблице распределения Стьюдента находят
критическими (табличными) значениями t-критерия с учетом
принятого уровня значимости (обычно - 0,01; 0,05; 0,10) и
числом степеней свободы вариации v=n-2.
5. шаг. Сравнивают фактическое и табличное значение. Если
фактическое значение (по модулю) больше табличного, то
соответствующий параметр признаётся значимым
(существенным).

32. Алгоритм построения F-критерий Фишера:

1. шаг. Выдвигается нулевая гипотеза об одновременной
значимости нулю всех коэффициентов регрессии при
объясняющих переменных.
2. шаг. Проверка данной гипотезы осуществляется на
основе дисперсионного анализа сравнения
объясненной и остаточной дисперсий.
3. шаг. При выполнение предпосылок МНК построенная
F-статистика имеет распределение Фишера с числом
степеней свободы v1=m-1, v2=n-m.
4. шаг. Если при требуемом уровне значимости
Fфакт>Fтабл то Н0 отклоняется в пользу Н1.

33.

Этапы построения регрессионной модели
1 этап
2 этап
3 этап
4 этап
Экономические выводы
5 этап
6 этап