Similar presentations:
Закон сохранения энергии
1.
ЗАКОН СОХРАНЕНИЯЭНЕРГИИ
2.
ПОЛНАЯ МЕХАНИЧЕСКАЯЭНЕРГИЯ
• Полная механическая энергия системыэто энергия движения и
взаимодействия
E T U
3.
• Рассмотрим систему материальныхточек
m1 , m2 … mN
V1 , V2 … VN
…
F1in
FNin
-равнодействующая внутренних консервативных сил
…
F1out
FNout
-равнодействующая внешних консервативных сил
…
f1
fN
-равнодействующая внешних неконсервативных сил
4.
• Запишем для каждой точки уравнениядвижения
dV1
m1
F1in F1out f1
dt
…
…
…
…
dVN F F
mN
Nin Nout f N
dt
5.
• Умножим скалярно каждое уравнениена
dri Vi dt
dV1
( f dr )
1 1
m1 (V1dt
) ( F1in F1out )dr1
dt
+
…
…
…
…
dVN
mN (VN dt
) ( FNin FNout )drN ( f N drN )
dt
6.
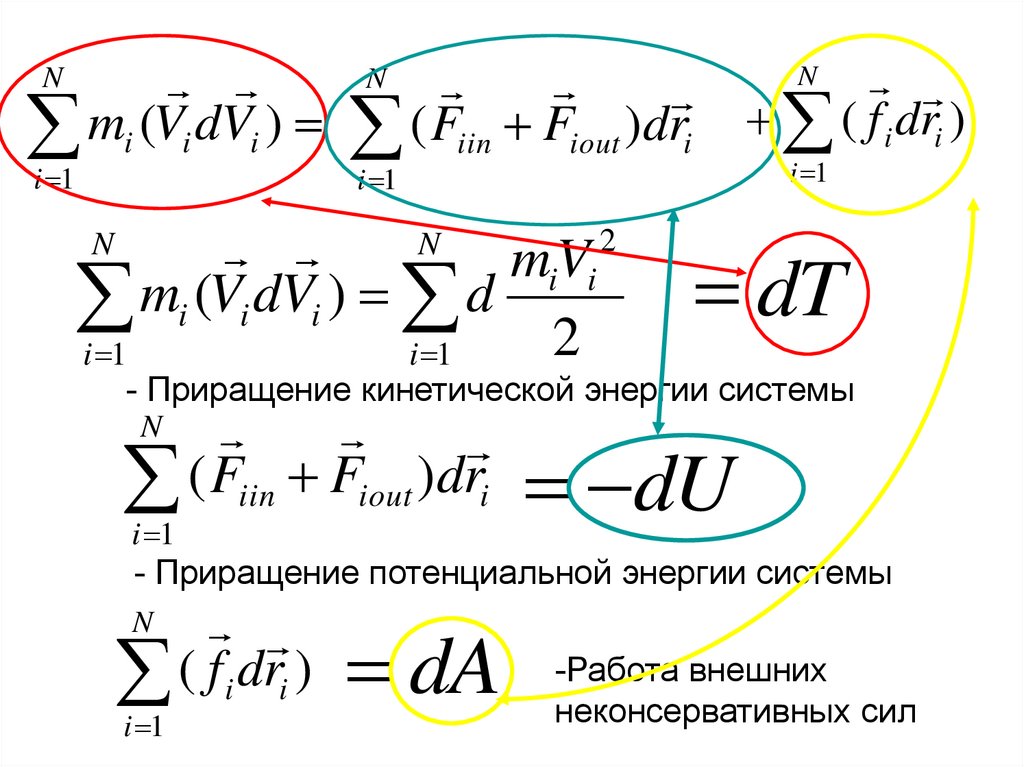
mi (Vi dVi )N
i 1
( f i dri )
( Fiin Fiout )dri
N
N
i 1
i 1
2
N
miVi
mi (Vi dVi ) d
2
i 1
i 1
N
dT
- Приращение кинетической энергии системы
( Fiin Fiout )dri
N
i 1
dU
- Приращение потенциальной энергии системы
( f i dri )
N
i 1
dA
-Работа внешних
неконсервативных сил
7.
dT dU dAd (T U ) dA
При переходе системы из состояния 1 в состояние 2
1
1
1
1
d (T U ) dA
8.
• Изменение полной энергии системыпри переходе из одного состояния в
другое равно работе внешних
неконсервативных сил
9.
• Если неконсервативные силыотсутствуют, то
d (T U ) 0
E T U const
• выполняется закон сохранения энергии
10.
Закон сохранения энергии• В системе тел, между которыми
действуют только консервативные
силы, полная механическая энергия
сохраняется ( не меняется со
временем).
• В таких системах возможен лишь
переход энергии из одного вида в
другой
11.
КИНЕМАТИКА ТВЕРДОГОТЕЛА
12.
• Любое движение тела можнопредставить как сумму
поступательного движения и
вращательного движения вокруг
неподвижной оси
13.
Твердое тело• - расстояние между двумя любыми
точками которого не меняется в
процессе движения
14.
• Поступательное движение – прикотором любая прямая, проведенная
через произвольные точки тела
перемещается параллельно самой
себе.
15.
16.
• При этом все точки тела за одинаковыепромежутки времени совершают
одинаковые перемещения
• Скорости и ускорения всех точек
твердого тела одинаковы
17.
ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕТВЕРДОГО ТЕЛА ВОКРУГ
НЕПОДВИЖНОЙ ОСИ
18.
• Движение, при котором все точки теладвижутся по окружности, центры
которых лежат на одной прямой,
называемой осью вращения.
19.
20.
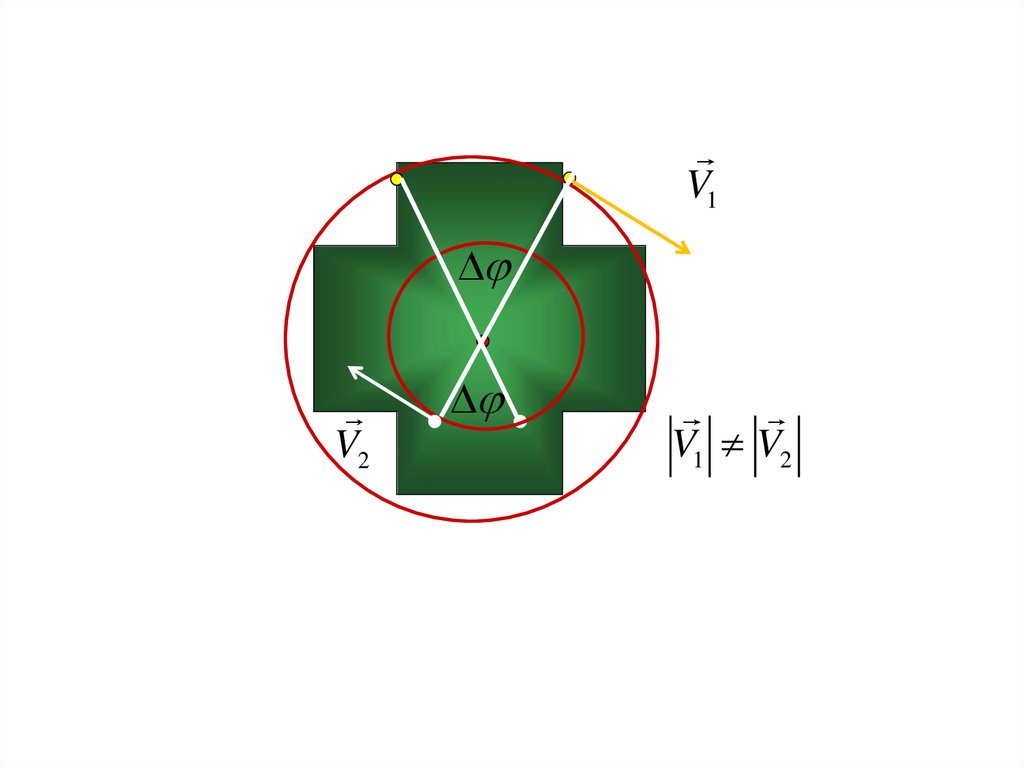
V1V2
V1 V2
21.
22.
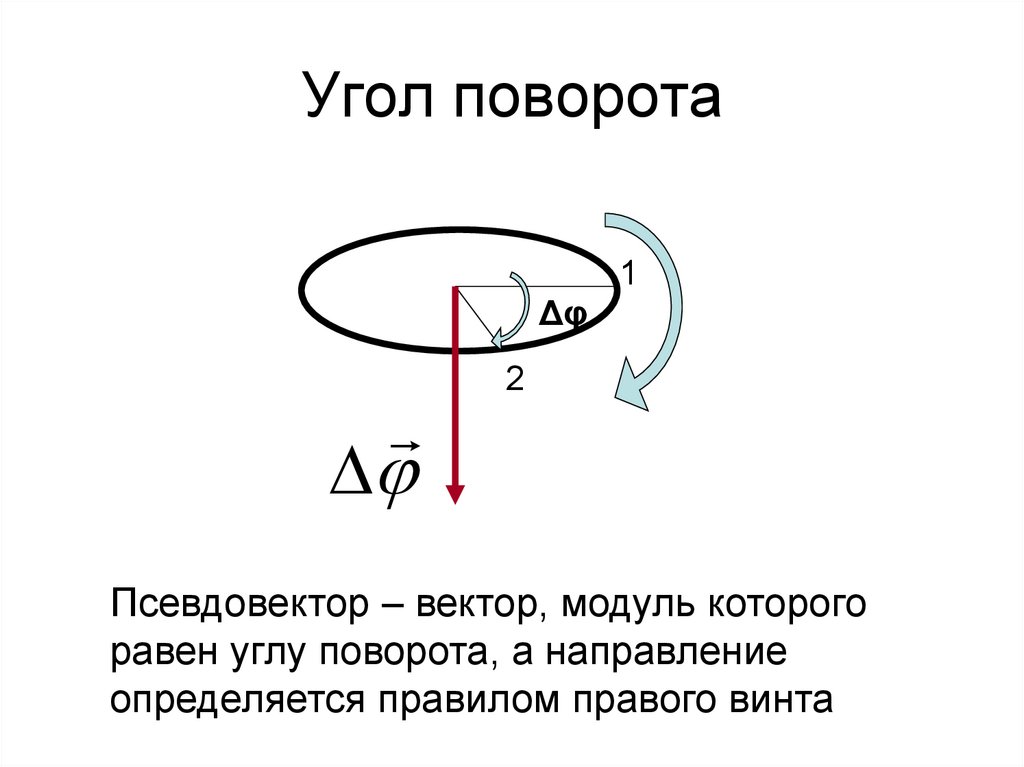
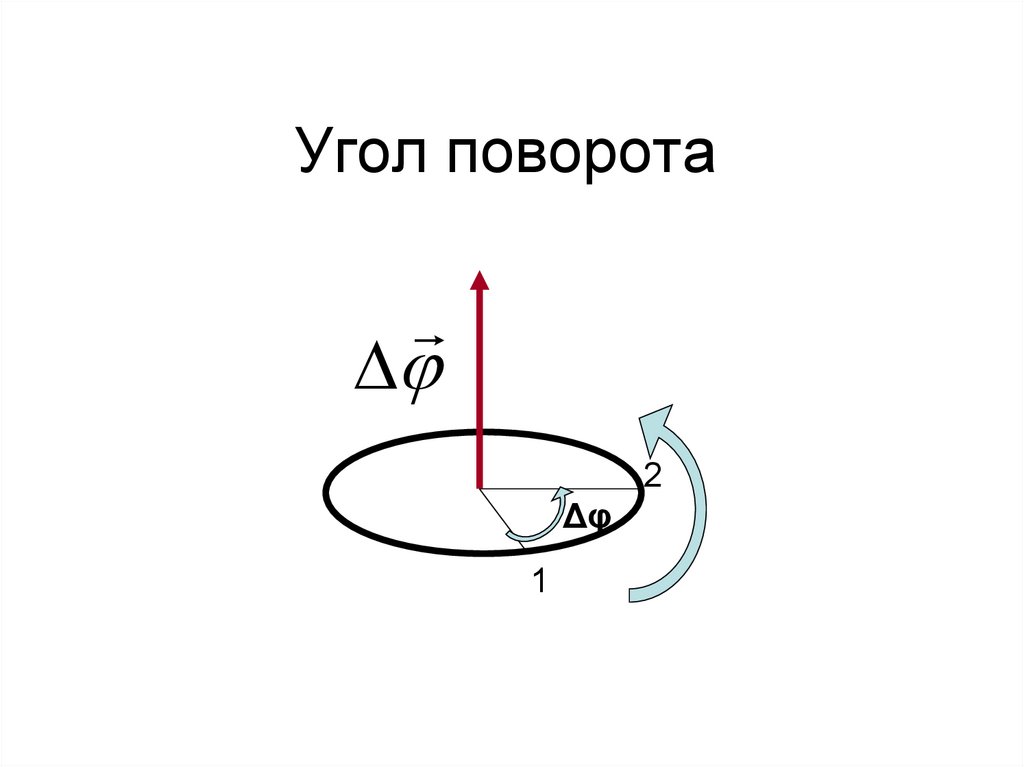
Угол поворота1
Δφ
2
Псевдовектор – вектор, модуль которого
равен углу поворота, а направление
определяется правилом правого винта
23.
Угол поворота2
Δφ
1
24.
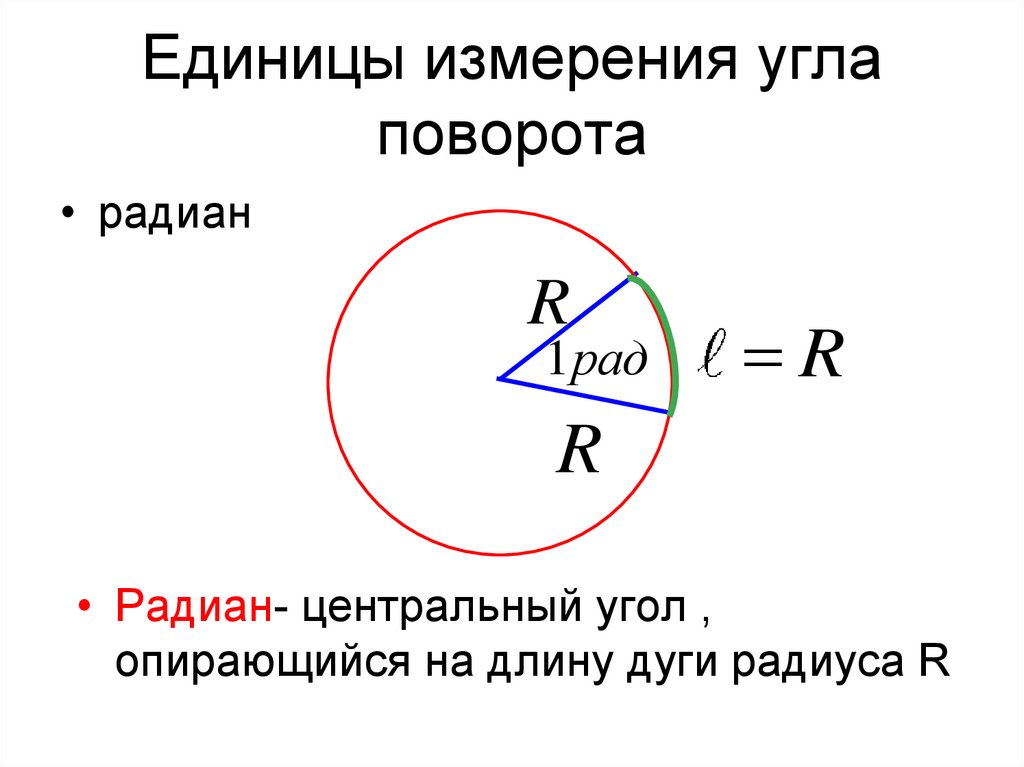
Единицы измерения углаповорота
• радиан
R
1рад
R
R
• Радиан- центральный угол ,
опирающийся на длину дуги радиуса R
25.
R1рад
2R
0,5R
0,5 рад
R
рад
2 рад
26.
• Если точка совершит полный оборот360 градусов
2 R
R
2
360 2
180
27.
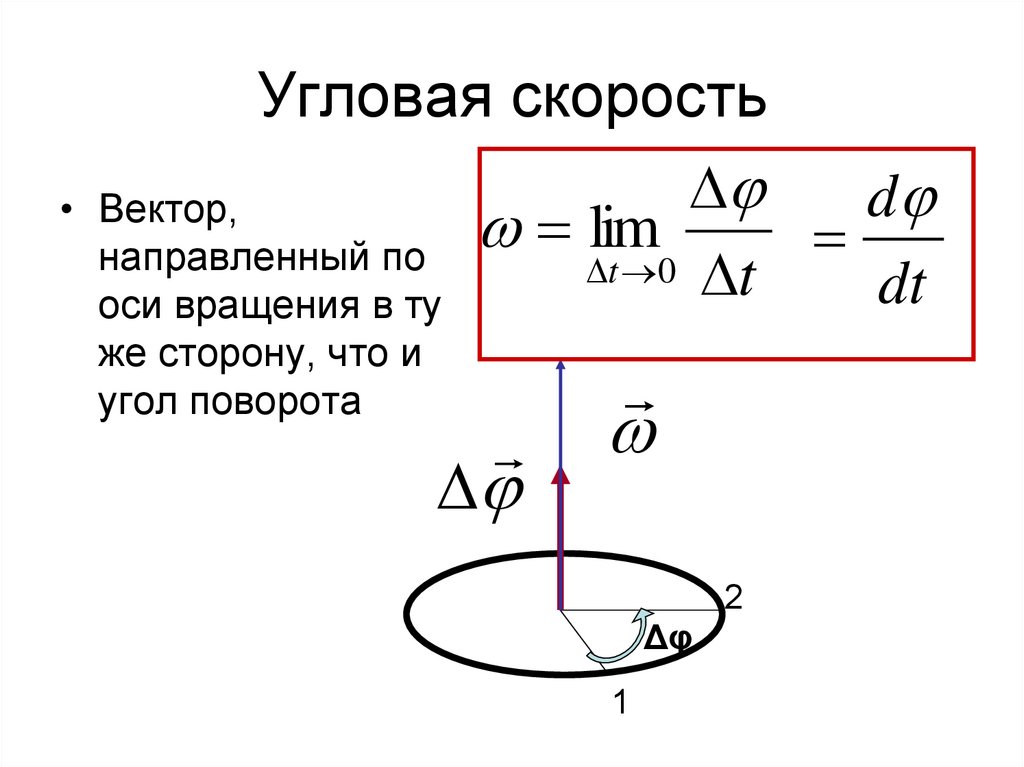
Угловая скорость
d
Вектор,
lim
направленный по
t 0 t
dt
оси вращения в ту
же сторону, что и
угол поворота
2
Δφ
1
28.
Единицы измеренияd
рад
dt
с
29.
ПЕРИОД ВРАЩЕНИЯ• Время, за которое точка совершает полный
оборот, т.е поворачивается на угол 2π
2
t
T
T
2
30.
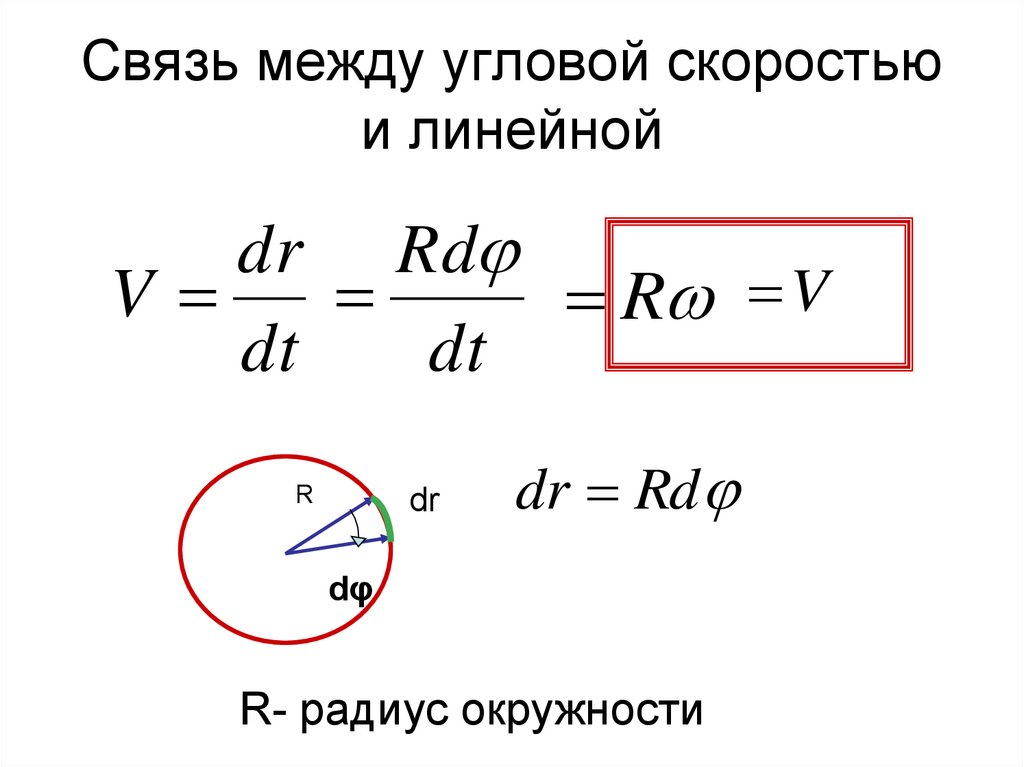
Связь между угловой скоростьюи линейной
dr Rd
V
R V
dt
dt
R
dr
dr Rd
dφ
R- радиус окружности
31.
Угловое ускорениеd d
2
dt dt
2
32.
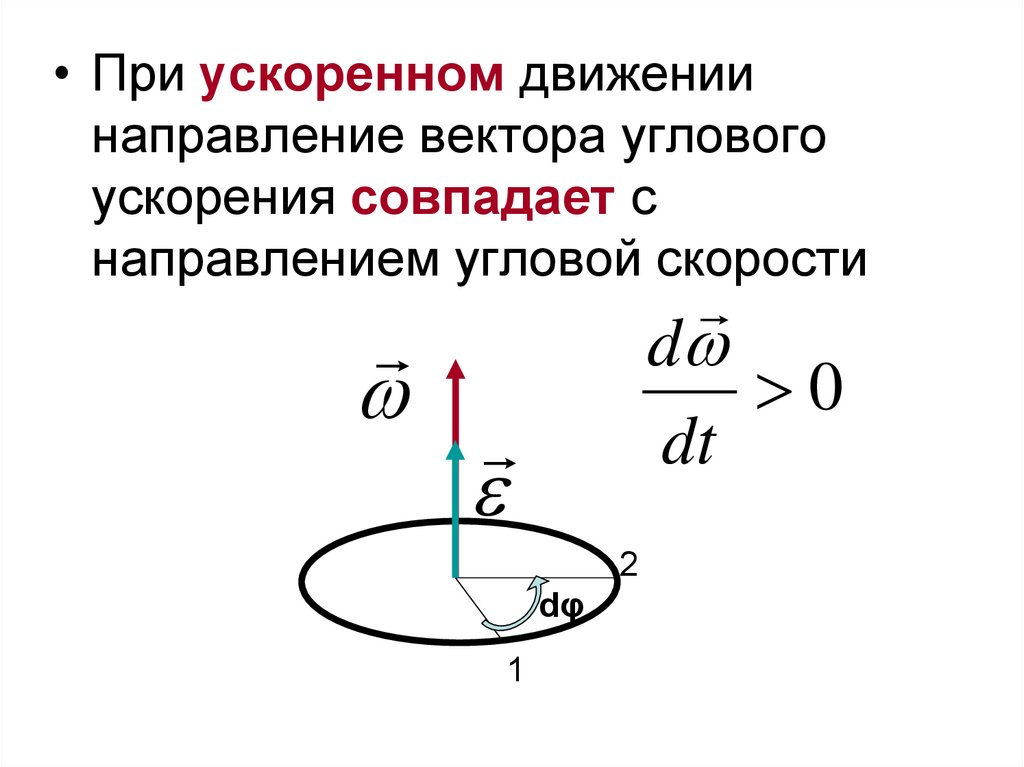
• При ускоренном движениинаправление вектора углового
ускорения совпадает с
направлением угловой скорости
d
0
dt
2
dφ
1
33.
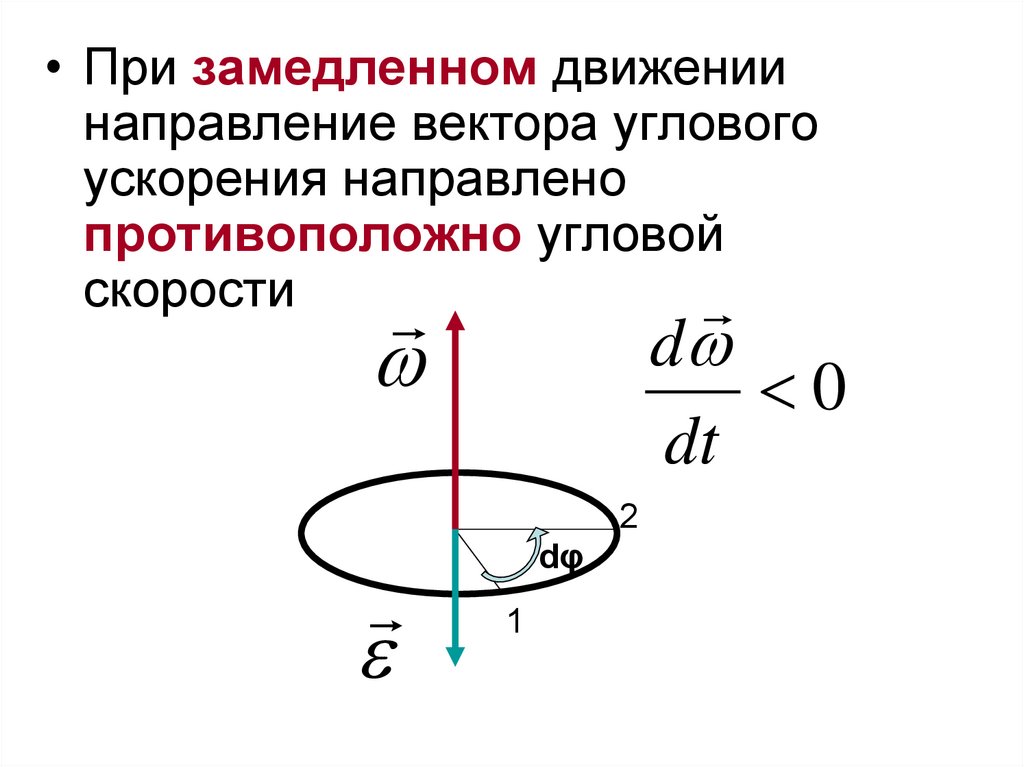
• При замедленном движениинаправление вектора углового
ускорения направлено
противоположно угловой
скорости
d
0
dt
2
dφ
1
34.
Тангенциальное ускорение• Направлено по касательной
• к окружности
dV
V R
a
dt
d
d ( R)
R
a
R a
dt
dt
35.
Нормальное ускорение• Направлено к центру
окружности
V
R
an
R
R
2
2 2
R an
2
36.
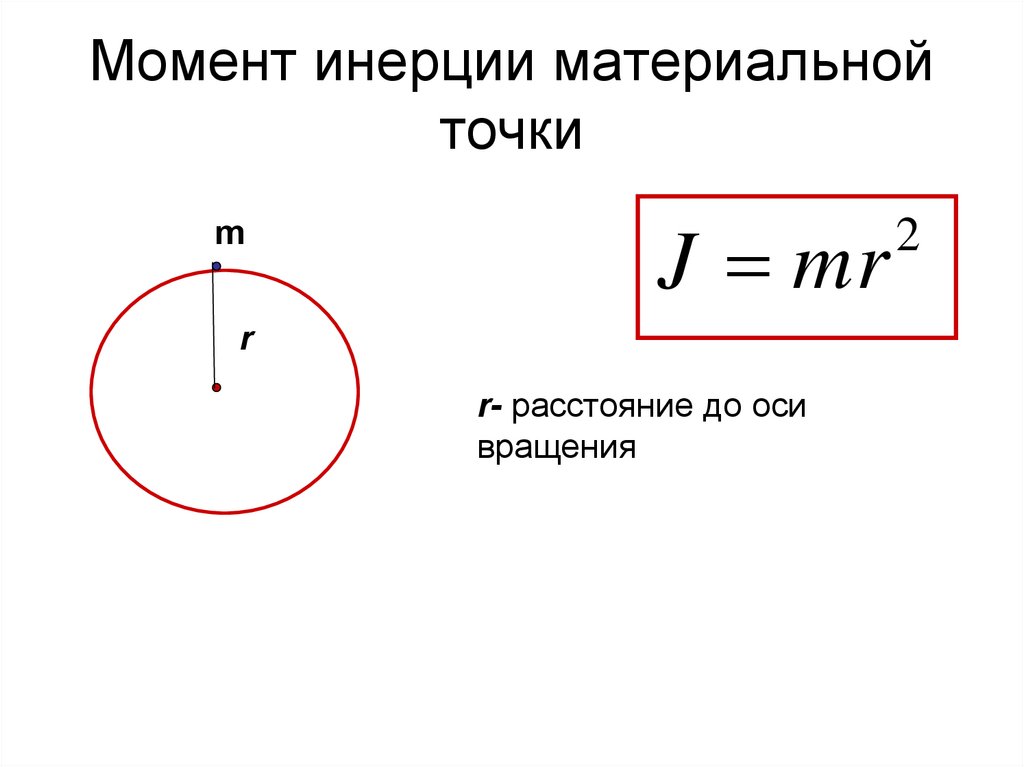
Момент инерции материальнойточки
m
J mr
r
r- расстояние до оси
вращения
2
37.
МОМЕНТ ИНЕРЦИИ СИСТЕМЫМАТЕРИАЛЬНЫХ ТОЧЕК
• Для системы
материальных точек
• mi- масса i
материальной точки
• ri – расстояние от i
материальной точки
до оси вращения
J mi ri
i
2
38.
• Для непрерывногораспределения
массы
J r dm
2
39.
ПРИМЕР• МОМЕНТ ИНЕРЦИИ ТОНКОГО КОЛЬЦА,
относительно оси, проходящей через его
центр (масса кольца m, радиус R)
J r dm
2
dm
R
R
R dm
2
R
2
dm
mR
2
40.
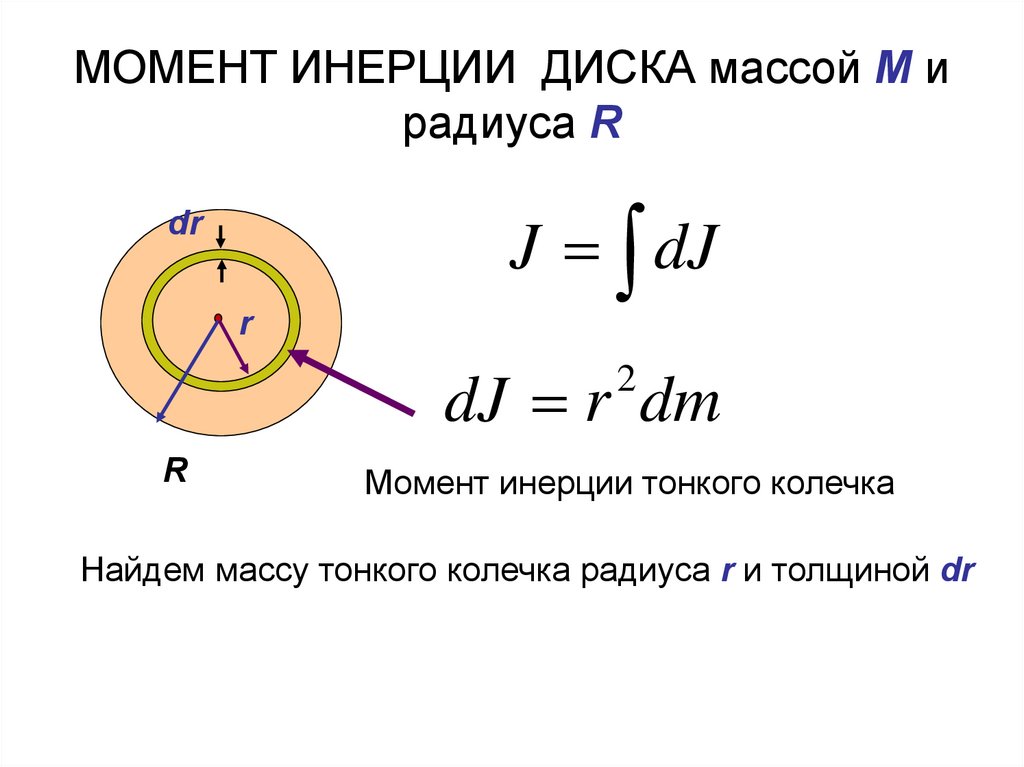
МОМЕНТ ИНЕРЦИИ ДИСКА массой M ирадиуса R
dr
r
J dJ
dJ r dm
2
R
Момент инерции тонкого колечка
Найдем массу тонкого колечка радиуса r и толщиной dr
41.
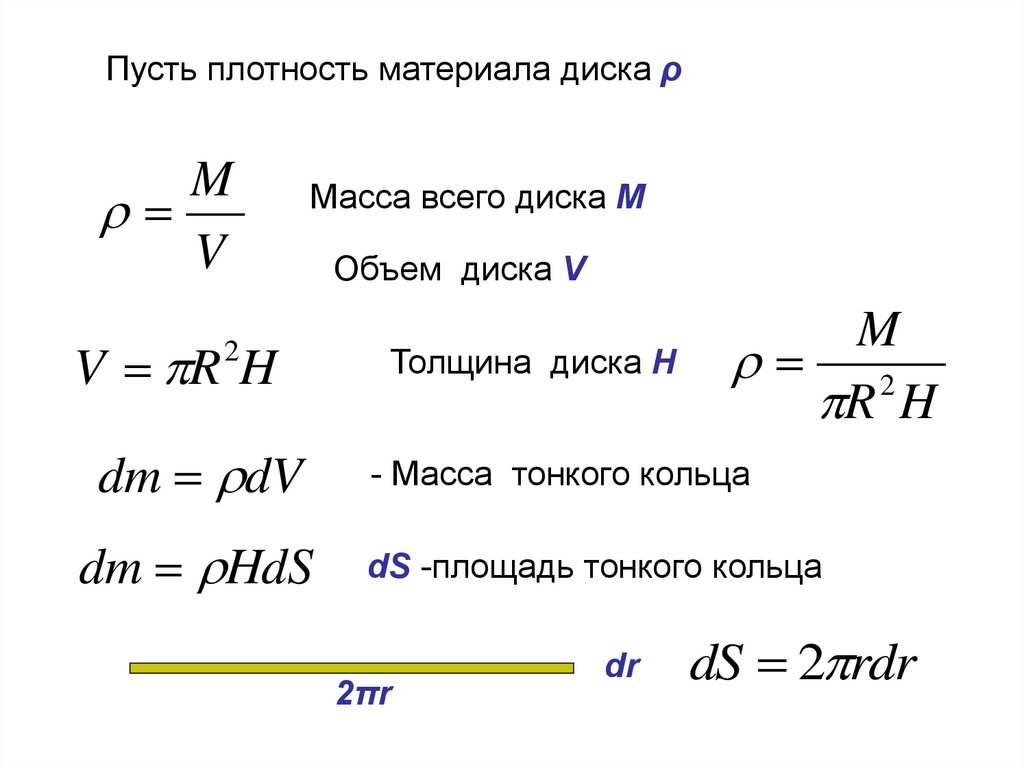
Пусть плотность материала диска ρM
V
Масса всего диска M
V R H
2
dm dV
dm HdS
Объем диска V
Толщина диска H
M
2
R H
- Масса тонкого кольца
dS -площадь тонкого кольца
2πr
dr
dS 2 rdr
42.
dJ r dmM
dm 2 rdr H R 2 H
M
dm 2 2 rdr H
R H
2 2 Mrdr
dJ r
2
R
R
3
2 Mr dr 2M 3
r
d
r
J dJ
2
2
R 0
R
2
43.
4 R2M r
J 2
R 4
0
MR
2
2
4
2M R
2
R
4
J
44.
Момент инерции тонкого стержня массыM и длиной L относительно оси,
проходящей через его центр
J x dm
2
x
dx
L
dm
Пусть линейная плотность стержня ρ
dm dx
M
L
45.
L2
M
2
J x dx
2 x dx
L
0
2
3
M x
2
L 3
L
0
L
2
M 2
2
L
3
3
2
ML
12
46.
Моменты инерции некоторых тел47.
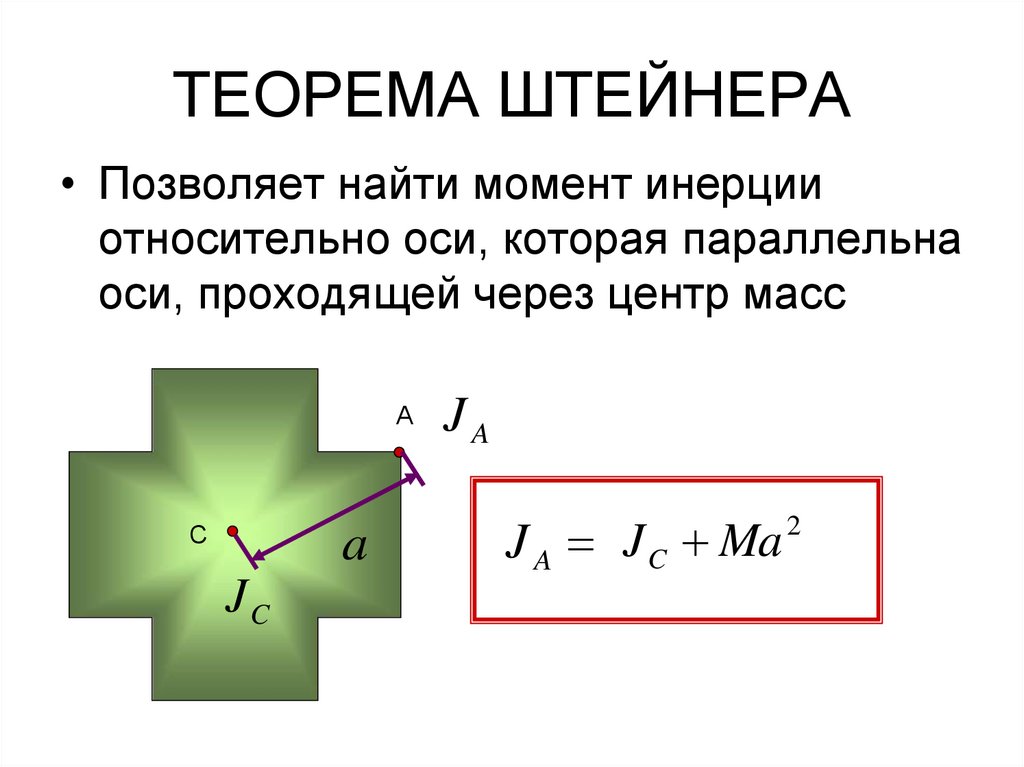
ТЕОРЕМА ШТЕЙНЕРА• Позволяет найти момент инерции
относительно оси, которая параллельна
оси, проходящей через центр масс
А
С
a
JC
JA
J A J C Ma
2
48.
Момент инерции тонкого стержняотносительно оси, проходящей
через край стержня,
перпендикулярно ему
JC
JA
С
L
2
ML
JA
3
А
J A J C Ma
2
2
L
a
2
12
2
2
2
ML
ML ML
JA
3
4
12
J C ML
49.
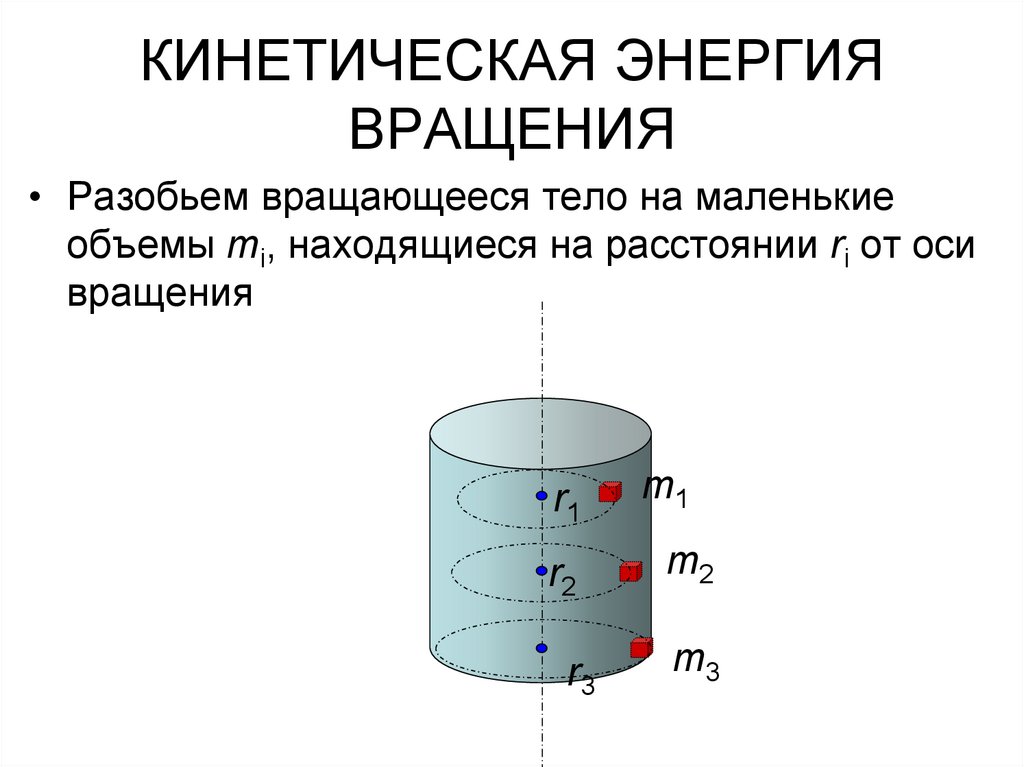
КИНЕТИЧЕСКАЯ ЭНЕРГИЯВРАЩЕНИЯ
• Разобьем вращающееся тело на маленькие
объемы mi, находящиеся на расстоянии ri от оси
вращения
r1
r2
r3
m1
m2
m3
50.
• Центры окружностей лежат на оси вращения(по определению)
• Угловая скорость вращения этих объемов
одинакова, а линейная - различна
V1 V2
r1
r2
51.
• Кинетическая энергия вращающегося тела2
1 1
2
2 2
mV
mV
Tвр
2
2
Vi ri
mi ri 2 2
Tвр
2
2
i
2
i
miVi
i 2
J
mi ri
2
2
J – момент инерции тела
2
2
Tв р
52.
• В случае плоского движения твердоготела кинетическая энергия складывается
из кинетической энергии поступательного
движения и кинетической энергии
вращательного движения
mV
J C
T
2
2
2
C
2
VC- скорость поступательного
движения центра масс
JC- Момент инерции тела относительно оси,
проходящей через центр масс
53.
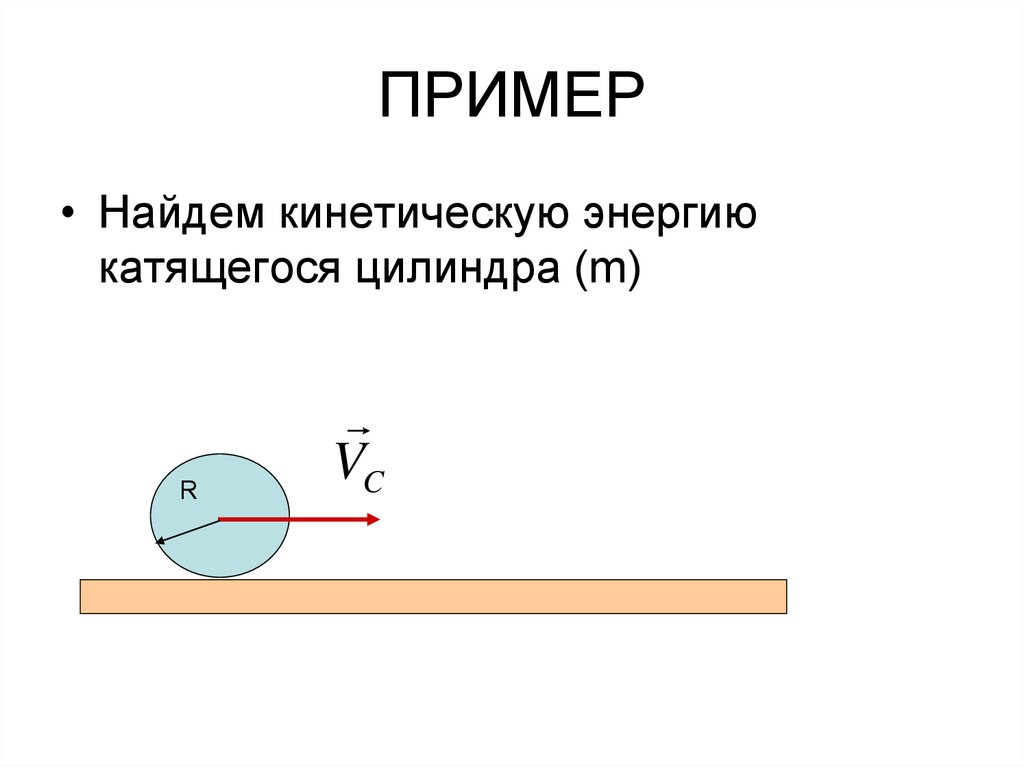
ПРИМЕР• Найдем кинетическую энергию
катящегося цилиндра (m)
R
VC
54.
mVJ C
T
2
2
2
C
2
mR 2
JC
2
VC
R
2
C
mV
1 mR
T
2
2 2
2
C
2
C
mV
mV
2
4
2
2
VC
2
R
2
C
3mV
4




























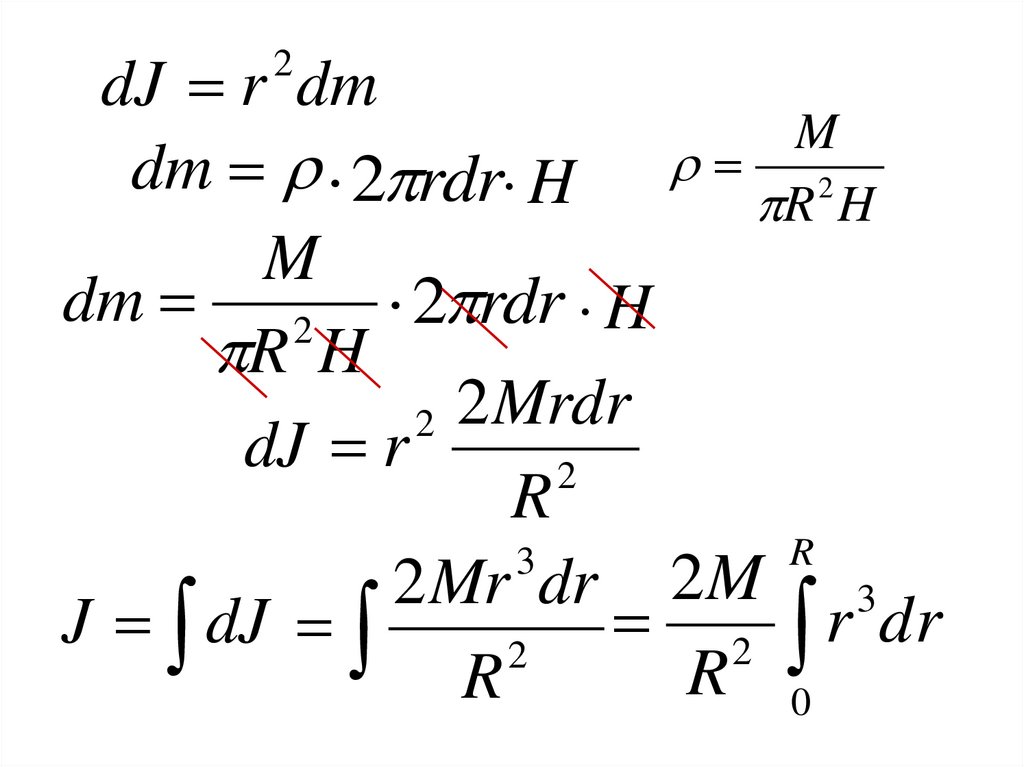


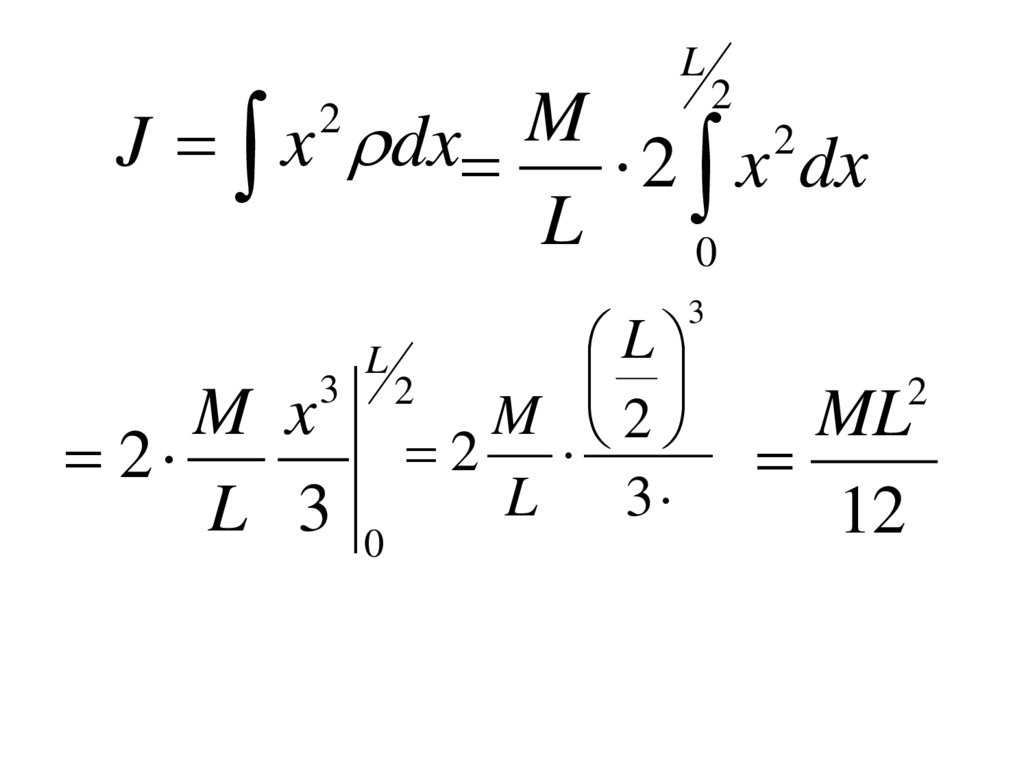





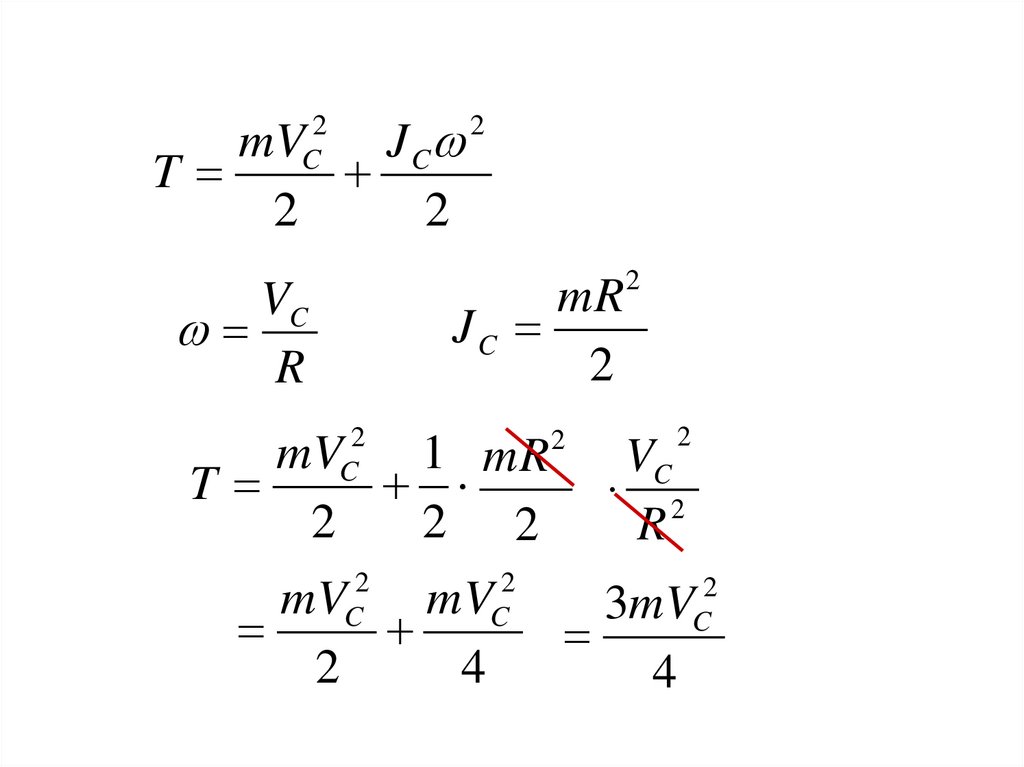
 physics
physics








