Similar presentations:
Решение метрических задач
1. Тема 2. Решение метрических задач
1. Способ замены плоскостей проекций.1.1. Определение действительного вида.
1.2. Определение углов.
1.3. Определение расстояний.
2. Способ вращения вокруг проецирующей оси.
3. Определение длины отрезка прямой
различными способами.
1
2.
К метрическим задачам относятся :•Задачи на определение действительного вида
(натуральной величины) отрезка прямой или плоской
фигуры;
•Задачи на определение углов (наклона отрезка прямой
к плоскости, между двумя плоскими фигурами т.п.);
•Задачи на определение расстояний между объектами
проецирования ( точкой и прямой, двумя прямыми,
прямой и плоскостью, двумя плоскостями и т.п.)
2
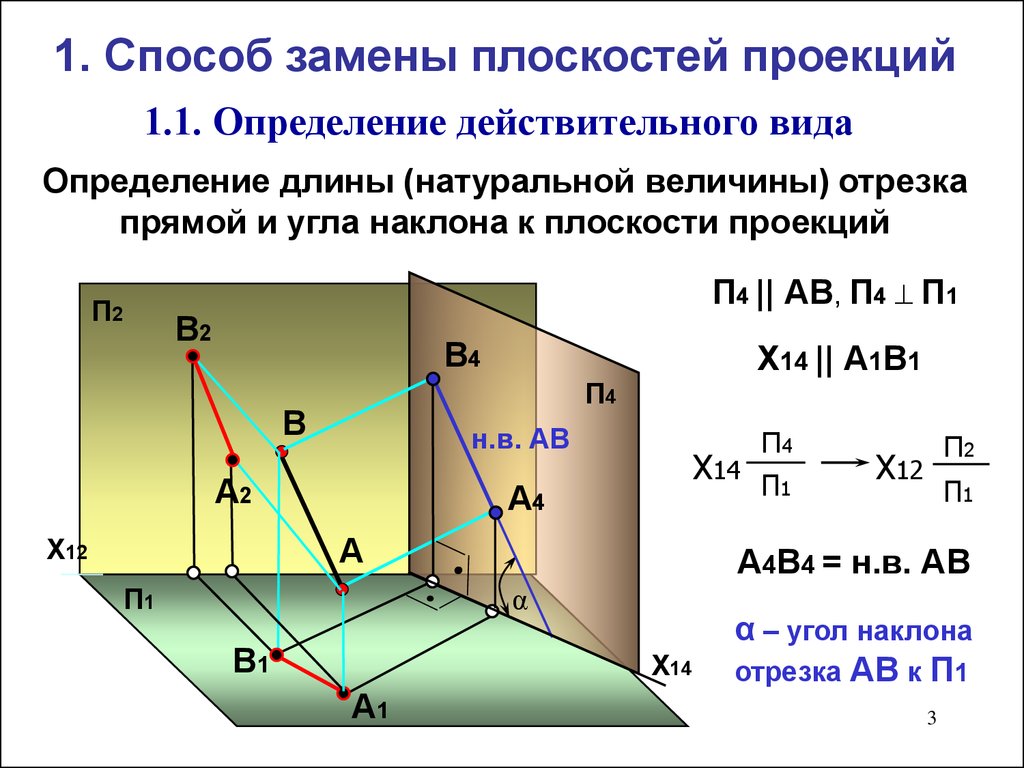
3. Определение длины (натуральной величины) отрезка прямой и угла наклона к плоскости проекций
1. Способ замены плоскостей проекций1.1. Определение действительного вида
Определение длины (натуральной величины) отрезка
прямой и угла наклона к плоскости проекций
П2
П4 || АВ, П4 П1
В2
В4
Х14 || А1В1
П4
В
н.в. АВ
А2
П4
Х14 П1
А4
А
Х12
П1
X14
А1
Х12
П1
А4В4 = н.в. АВ
α
В1
П2
α – угол наклона
отрезка АВ к П1
3
4. Определение натуральной величины и углов наклона к плоскостям проекций на комплексном чертеже
В5Х25
Н.В.
АВ
В2
Х12
П5
А2 П2
П2
П1
А5
Х14 || А1В1
Х12
Х14
А1А4 Х14; В1В4 Х14
α – угол наклона
отрезка АВ к П1
Х25 || А2В2
В1
Х14
α
В4
Х25
А1
Н.В.
АВ
П1
А4 П4
Х12
А2А5 Х25; В2В5 Х25
– угол наклона
отрезка АВ к П2
4
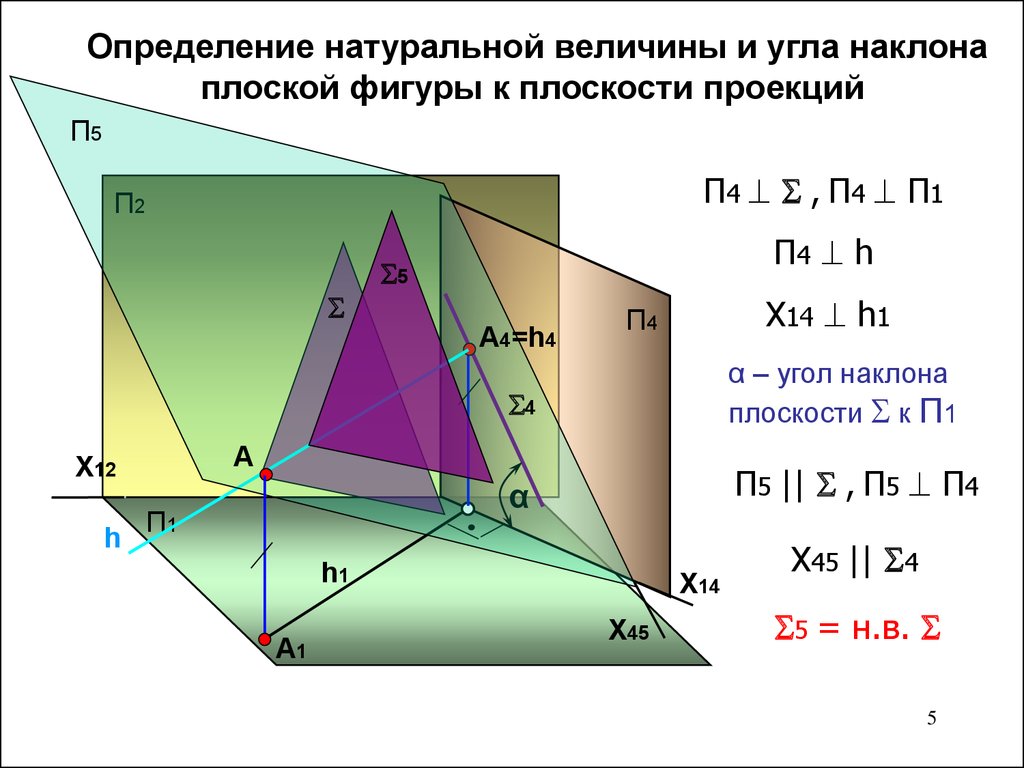
5. Определение натуральной величины и угла наклона плоской фигуры к плоскости проекций
П5П4 , П4 П1
П2
А4=h4
X14 h1
П4
4
α – угол наклона
плоскости к П1
α
П5 || , П5 П4
А
Х12
h
П4 h
5
П1
h1
А1
X14
X45
X45 || 4
5 = н.в.
5
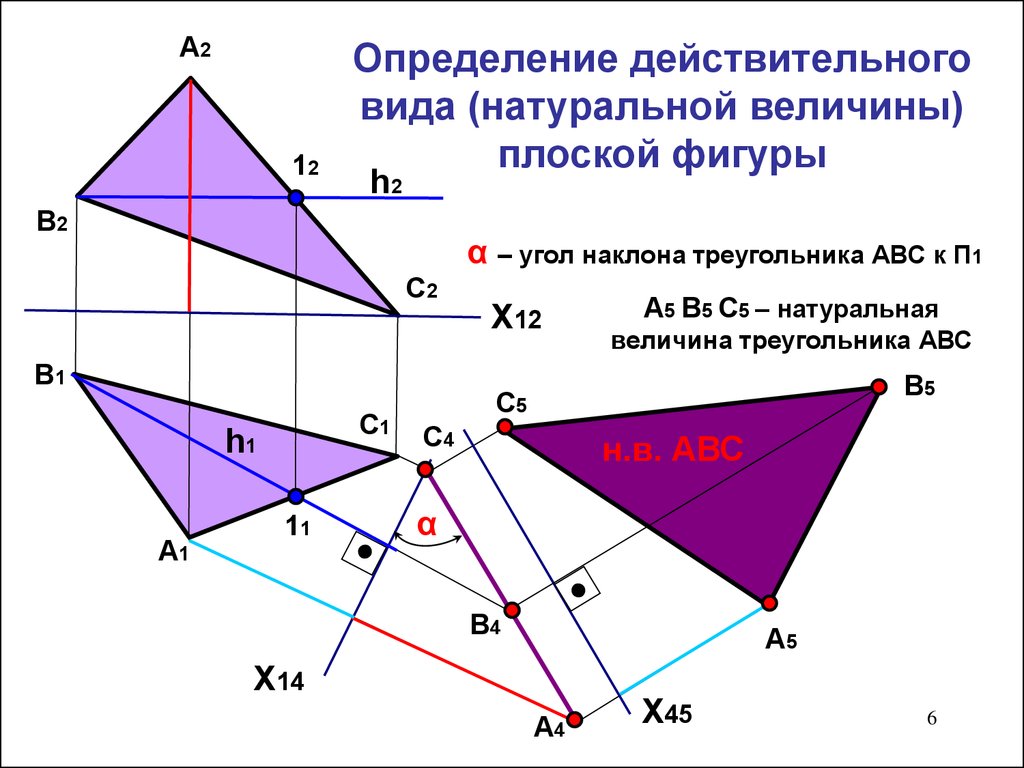
6. Определение действительного вида (натуральной величины) плоской фигуры
А212
Определение действительного
вида (натуральной величины)
плоской фигуры
h2
В2
α – угол наклона треугольника АВС к П1
С2
В1
С1
h1
А1
11
Х12
А5 В5 С5 – натуральная
величина треугольника АВС
В5
С5
С4
н.в. АВС
α
В4
А5
Х14
А4
Х45
6
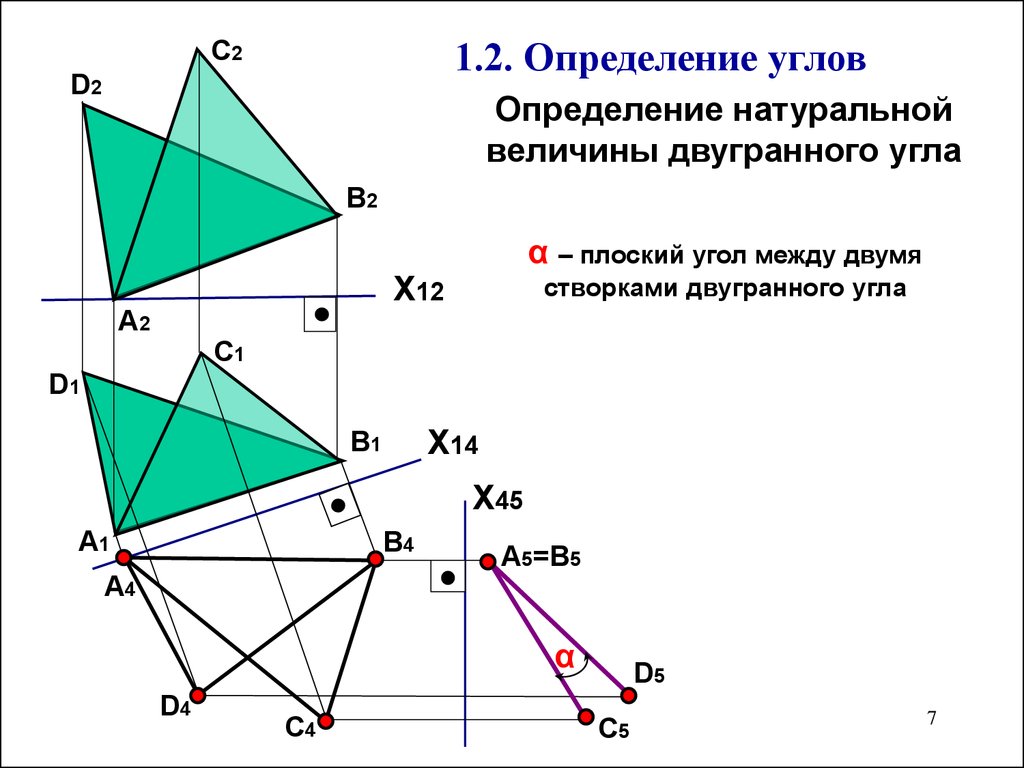
7. Определение натуральной величины двугранного угла
С21.2. Определение углов
D2
Определение натуральной
величины двугранного угла
В2
α – плоский угол между двумя
Х12
А2
створками двугранного угла
C1
D1
Х14
B1
Х45
А1
В4
А4
А5=В5
α
D4
С4
D5
С5
7
8. Определение расстояния от точки до плоскости
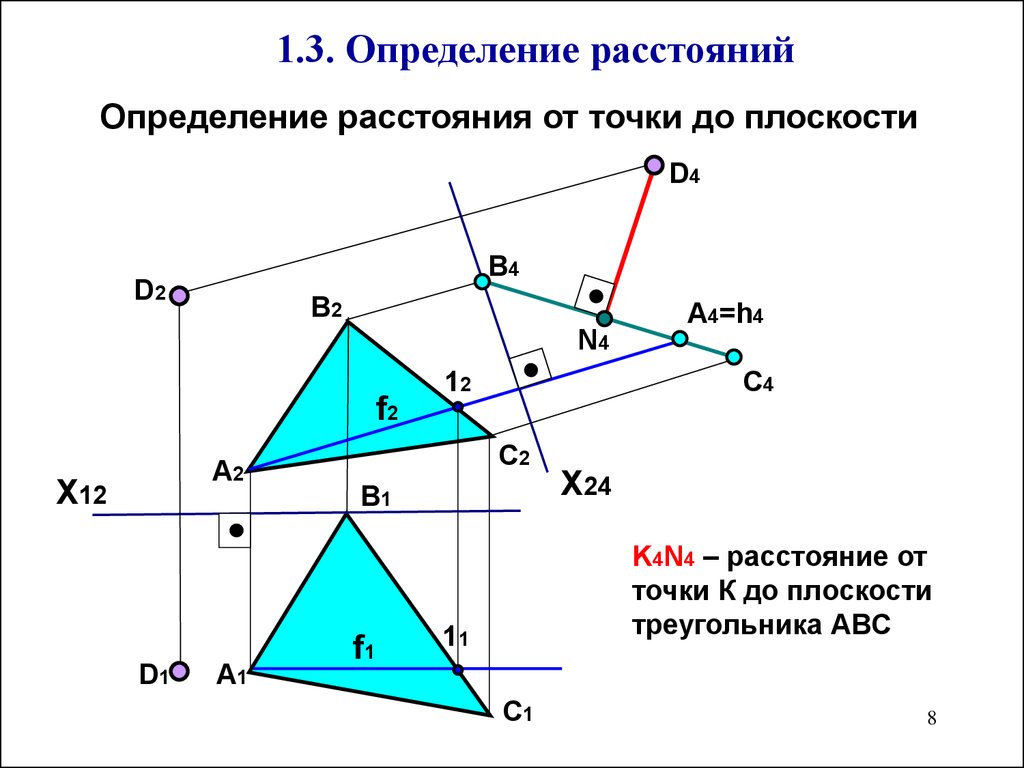
1.3. Определение расстоянийОпределение расстояния от точки до плоскости
D4
В4
D2
В2
А4=h4
N4
f2
А2
Х12
D1
А1
С4
12
С2
В1
f1
Х24
K4N4 – расстояние от
точки К до плоскости
треугольника АВС
11
С1
8
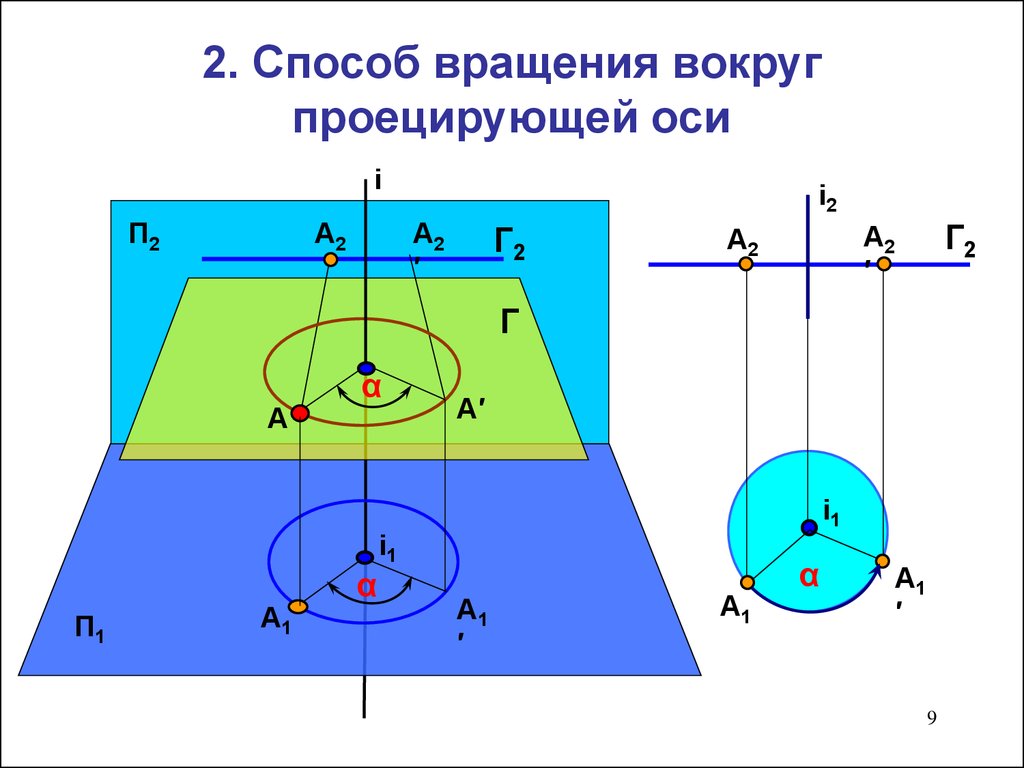
9. 2. Способ вращения вокруг проецирующей оси
iП2
А2
i2
А2
′
Г2
Г2
А2
′
А2
Г
А
α
А′
i1
П1
А1
α
i1
А1
′
А1
α
А1
′
9
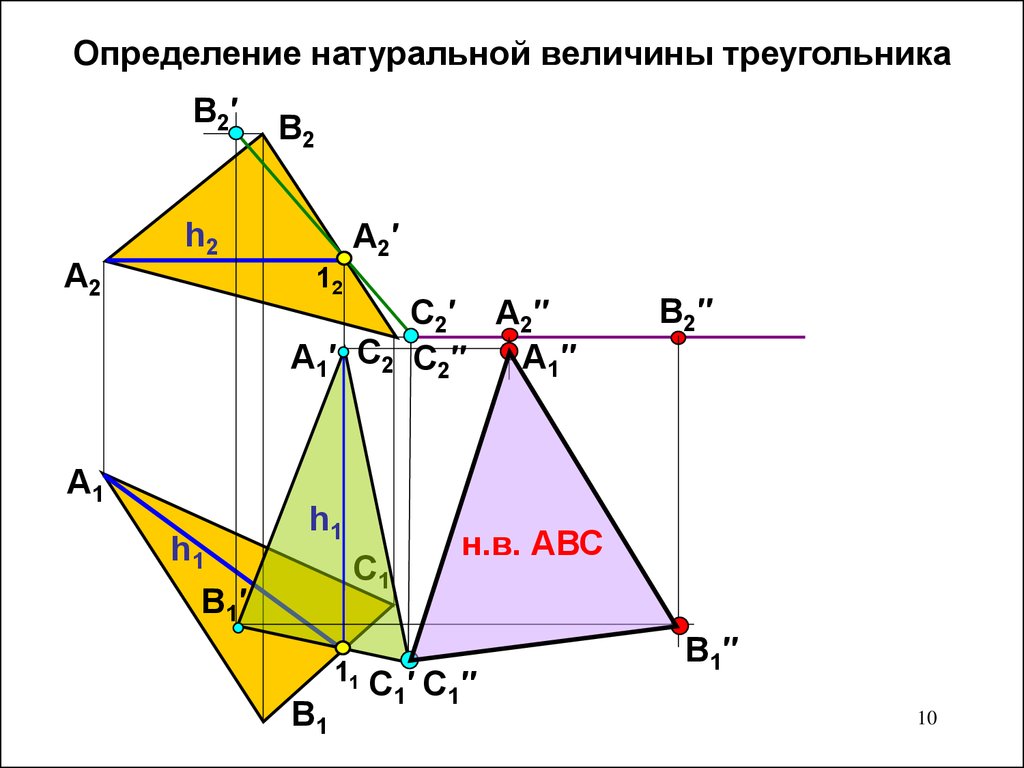
10. Определение натуральной величины треугольника
В2′А2
В2
А2′
h2
12
С2′ А2′′
А1′ С2 С2′′
А1′′
А1
h1
h1
С1
В1′
В1
В2′′
н.в. АВС
11 С ′ С ′′
1
1
В1′′
10
11. 3. Определение длины отрезка прямой различными способами
• Аналитическим• Прямоугольного треугольника
• Замены плоскостей проекций (см. слайд
№ 4)
• Вращения вокруг проецирующей оси
• Плоско-параллельного перемещения
• Монжа
11
12.
Способ прямоугольного треугольникаПусть заданы две точки с координатами А(40,30,20), В(10,20,40).
Требуется определить расстояние между ними, т.е. длину
(натуральную величину) отрезка, ими ограниченного.
Аналитический вариант
Графический вариант
|AB|2 = (xA - xB)2 +
+ (yA -
yB)2
+
н.в. АВ
А0
yA-yB
+ (zB - zA)2
α = arcsin( (zB - zA)/|AB|)
zB-zA
хA-хB
А2
В1
|AB| = 37,4
Угол наклона АВ к П1
В2
zB-zA
yA-yB
α
А1
н.в. АВ
В0
12
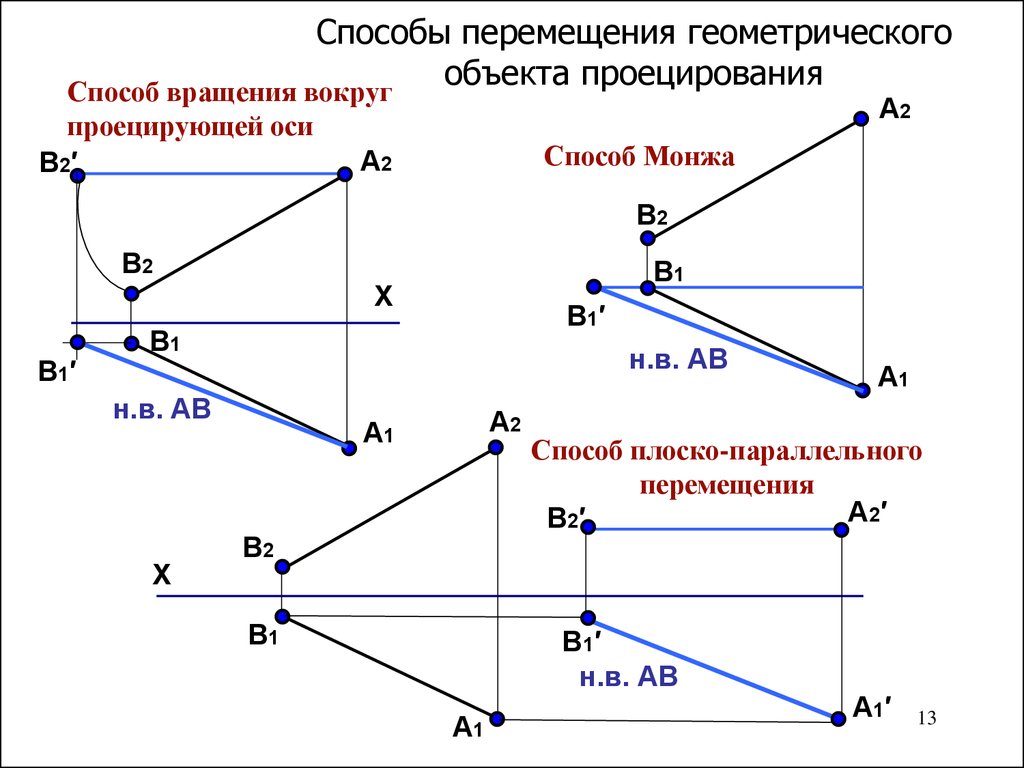
13. Способы перемещения геометрического объекта проецирования
Способ вращения вокругпроецирующей оси
В2′
А2
Способ Монжа
А2
В2
В2
В1
Х
В1′
В 1′
В1
н.в. АВ
н.в. АВ
Х
А2
А1
В2
В1
Способ плоско-параллельного
перемещения
А2′
В2′
В 1′
н.в. АВ
А1
А1
А1′
13





 drafting
drafting








