Начертательная геометрия. Краткий курс

1. Начертательная геометрия

Краткий курс
Автор лекций Белокрылова
Ольга Вениаминовна
Кафедра начертательной геометрии и технического
черчения

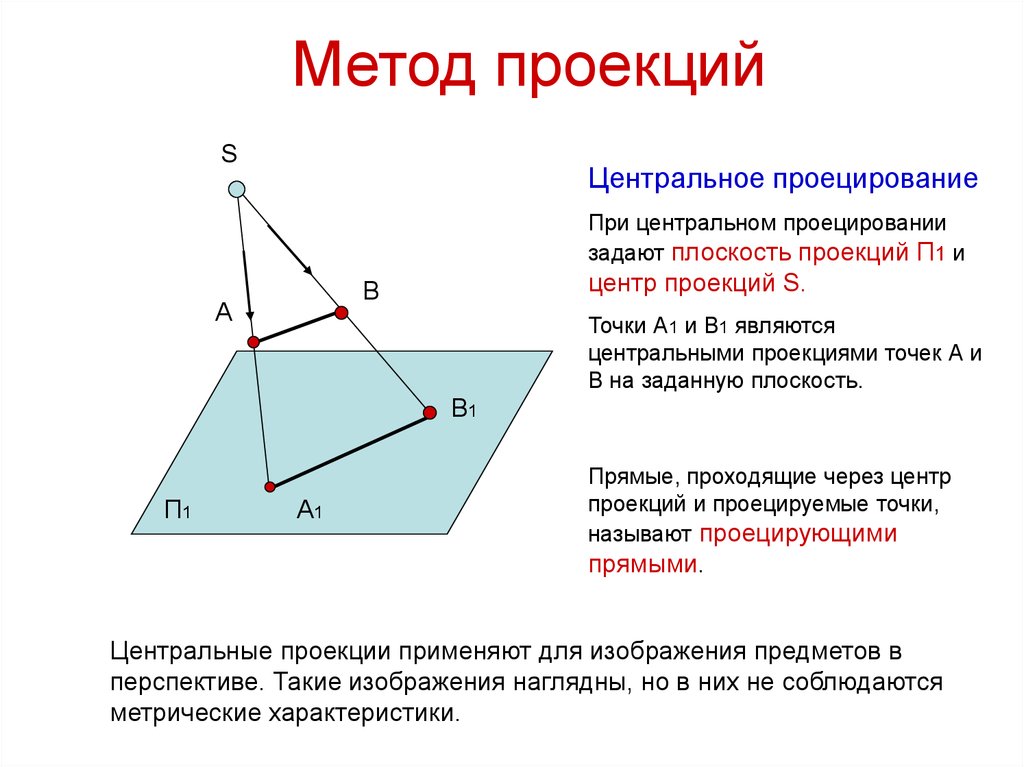
2. Метод проекций

S
Центральное проецирование
При центральном проецировании
задают плоскость проекций П1 и
центр проекций S.
В
А
Точки А1 и В1 являются
центральными проекциями точек А и
В на заданную плоскость.
В1
П1
А1
Прямые, проходящие через центр
проекций и проецируемые точки,
называют проецирующими
прямыми.
Центральные проекции применяют для изображения предметов в
перспективе. Такие изображения наглядны, но в них не соблюдаются
метрические характеристики.

3. Свойства центрального проецирования

• Точка проецируется в точку
• Прямая проецируется в прямую
• Двумерная фигура проецируется в виде
двумерной фигуры
• Трехмерная фигура отображается двумерной
• Центральные проекции фигур сохраняют
взаимную принадлежность, непрерывность и
другие геометрические свойства

4. Параллельные проекции

S
А
При параллельном проецировании центр
проецирования удален в бесконечность.
К
В
Проецирующие прямые параллельны
между собой. В зависимости от угла
наклона проецирующей прямой к
плоскости проекций параллельные
проекции разделяются на косоугольные и
прямоугольные или ортогональные.
В1
П1
А1
К1
К уже существующим возникают новые свойства:
- если прямые параллельны, то их проекции тоже
параллельны
-если точка К делит отрезок АВ в некотором
отношении, то проекция К1 делит А1В1 в том же
отношении
-геометрические образы параллельные плоскости
проекций проецируются на неё в натуральную
величину

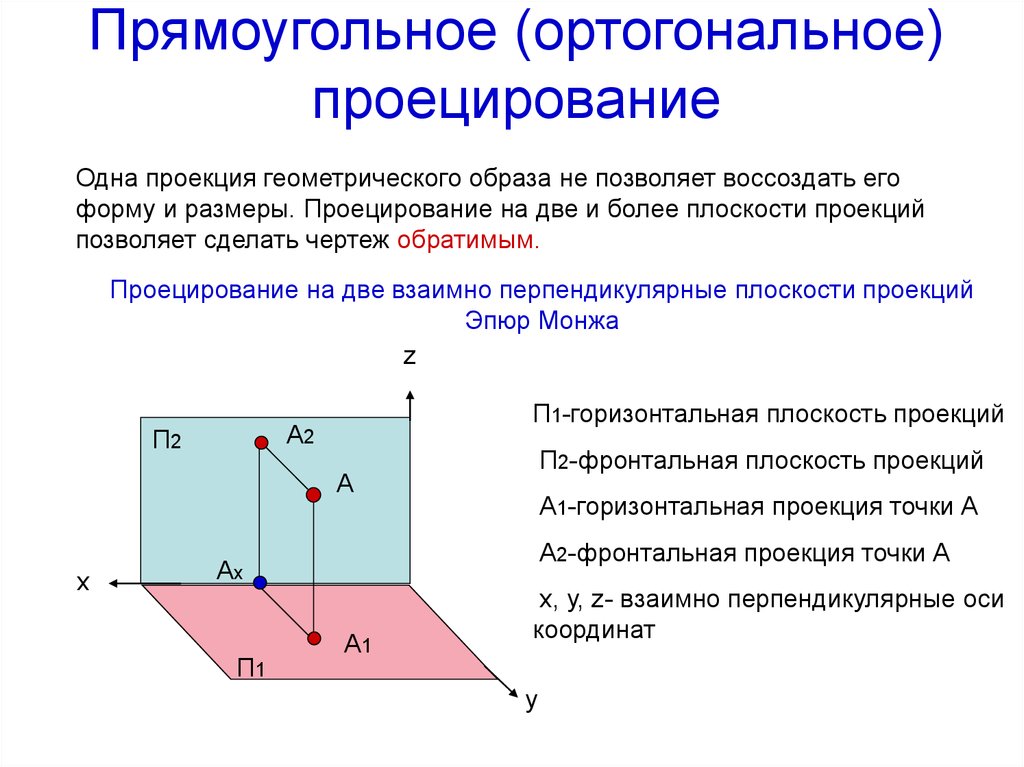
5. Прямоугольное (ортогональное) проецирование

Одна проекция геометрического образа не позволяет воссоздать его
форму и размеры. Проецирование на две и более плоскости проекций
позволяет сделать чертеж обратимым.
Проецирование на две взаимно перпендикулярные плоскости проекций
Эпюр Монжа
z
П1-горизонтальная плоскость проекций
А2
П2
П2-фронтальная плоскость проекций
А
x
А2-фронтальная проекция точки А
Ах
П1
А1-горизонтальная проекция точки А
А1
x, y, z- взаимно перпендикулярные оси
координат
y

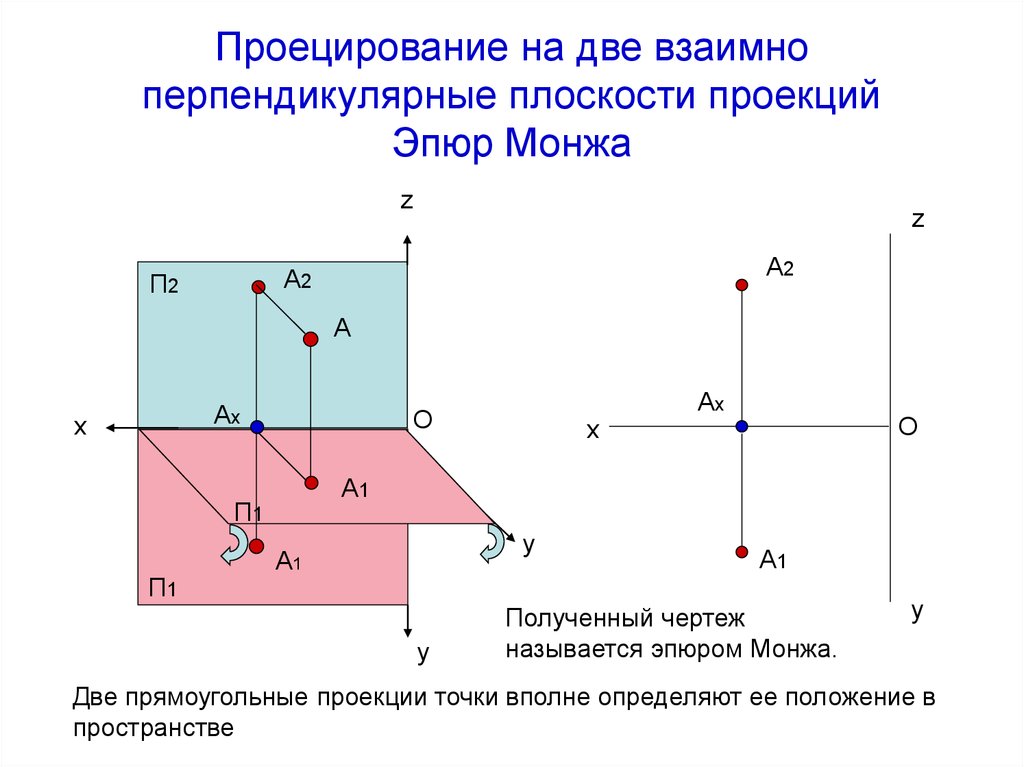
6. Проецирование на две взаимно перпендикулярные плоскости проекций Эпюр Монжа

z
z
А2
А2
П2
А
Ах
x
О
О
А1
П1
П1
х
Ах
y
А1
у
А1
Полученный чертеж
называется эпюром Монжа.
y
Две прямоугольные проекции точки вполне определяют ее положение в
пространстве

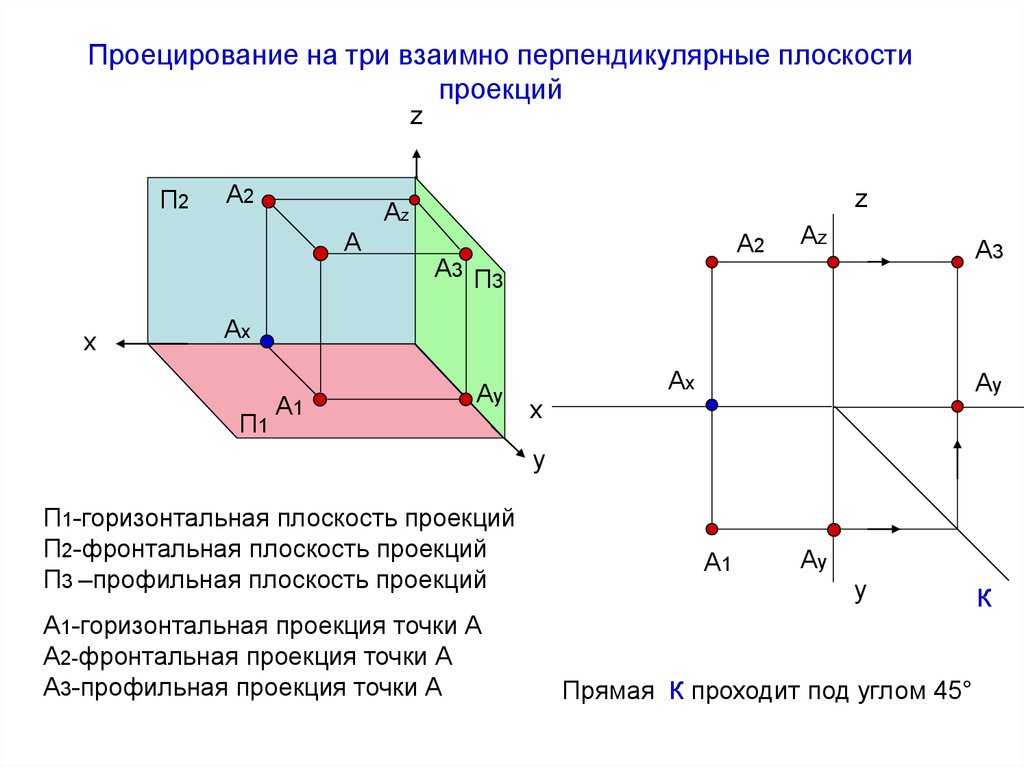
7. Проецирование на три взаимно перпендикулярные плоскости проекций

z
П2
А2
А
x
z
Аz
А2
А3 П3
Az
А3
Ах
П1
А1
Ау
Ах
Ау
х
y
П1-горизонтальная плоскость проекций
П2-фронтальная плоскость проекций
П3 –профильная плоскость проекций
А1-горизонтальная проекция точки А
А2-фронтальная проекция точки А
А3-профильная проекция точки А
А1
Ау
y
Прямая
к проходит под углом 45°
к

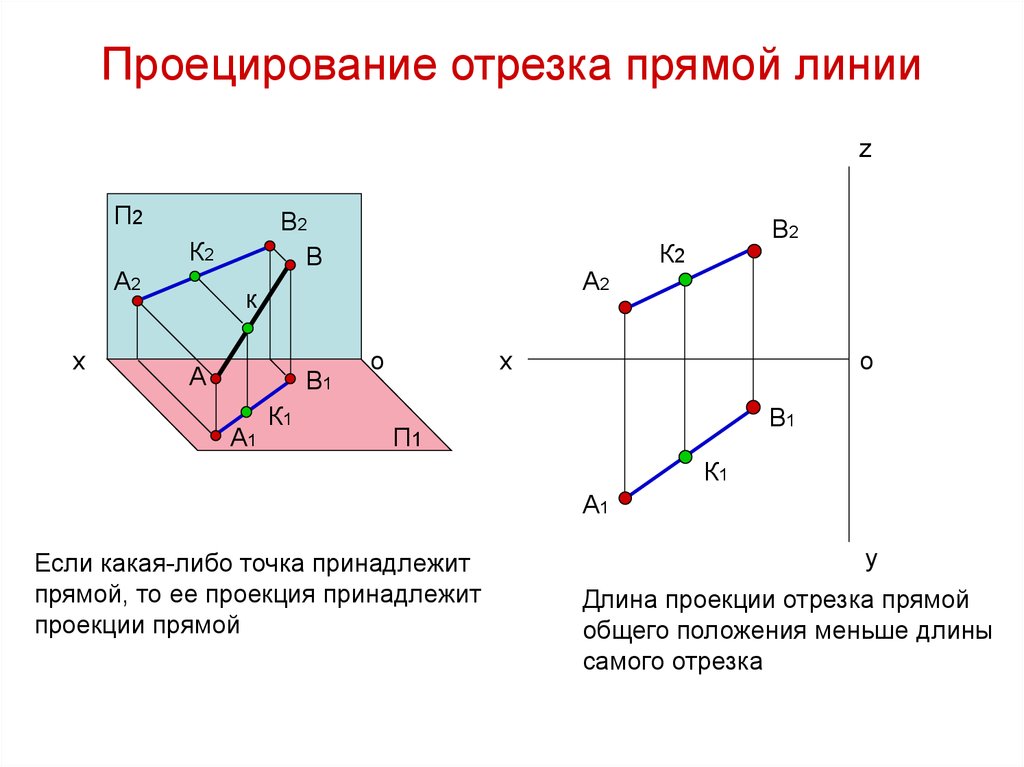
8. Проецирование отрезка прямой линии

z
П2
В2
В
К2
А2
х
А2
к
А
В1
А1
К1
о
В2
К2
х
о
В1
П1
К1
А1
Если какая-либо точка принадлежит
прямой, то ее проекция принадлежит
проекции прямой
y
Длина проекции отрезка прямой
общего положения меньше длины
самого отрезка

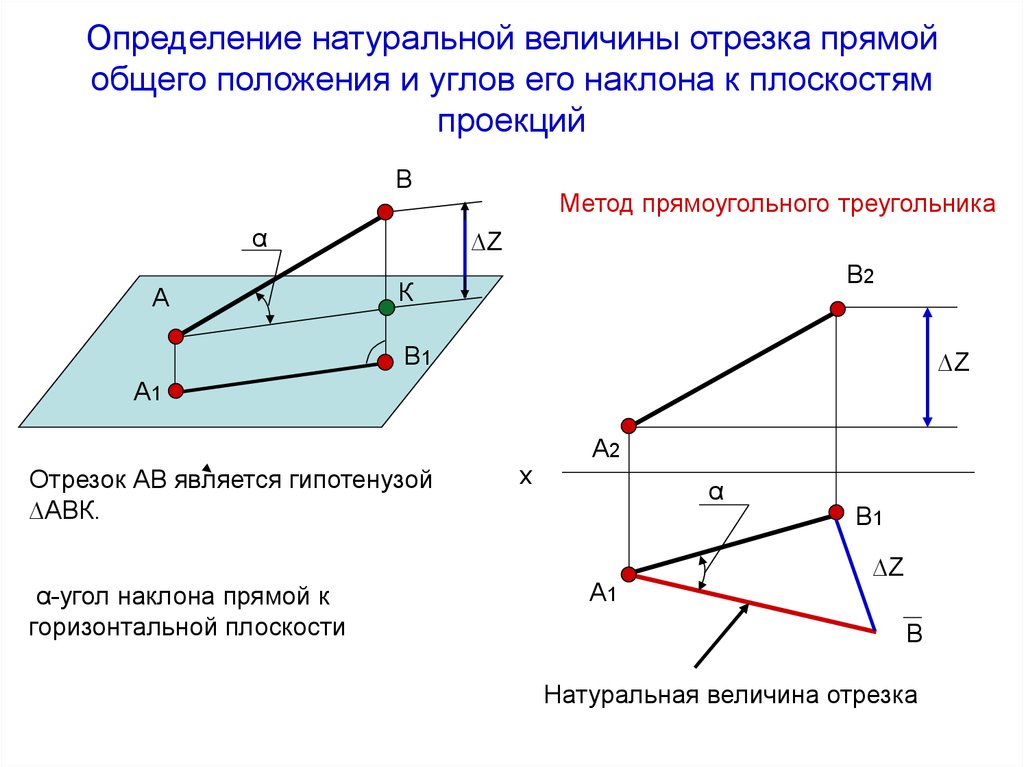
9. Определение натуральной величины отрезка прямой общего положения и углов его наклона к плоскостям проекций

В
α
А
Метод прямоугольного треугольника
∆Z
В2
К
В1
∆Z
А1
Отрезок АВ является гипотенузой
∆АВК.
α-угол наклона прямой к
горизонтальной плоскости
х
А2
α
А1
В1
∆Z
В
Натуральная величина отрезка

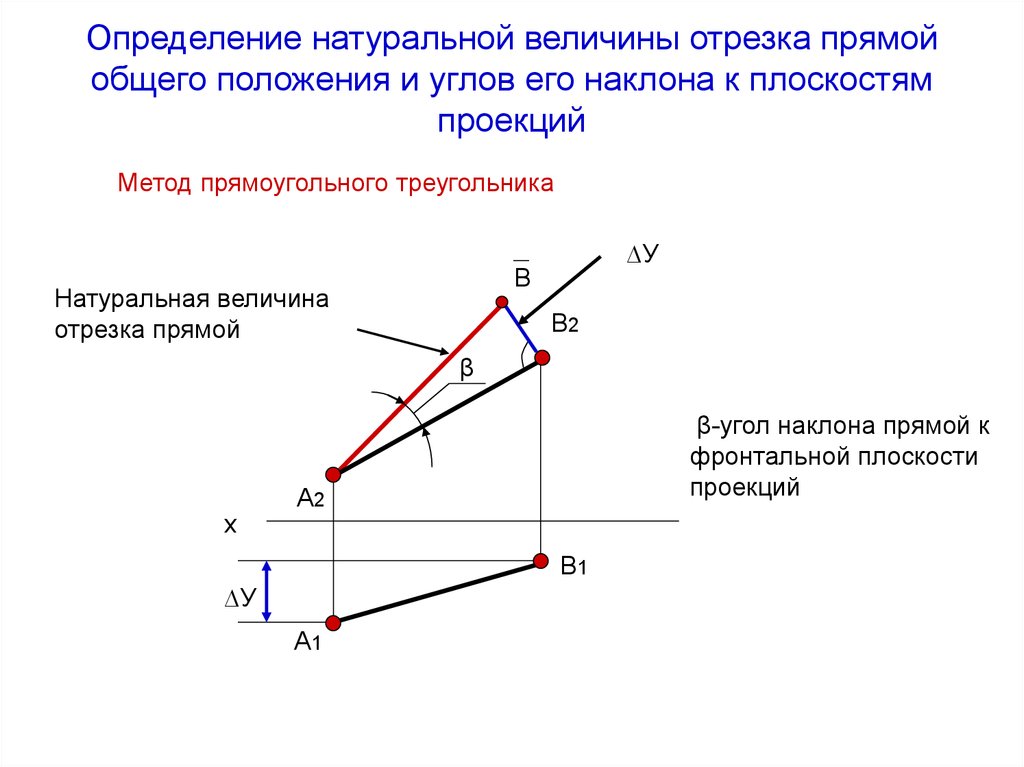
10. Определение натуральной величины отрезка прямой общего положения и углов его наклона к плоскостям проекций

Метод прямоугольного треугольника
∆У
В
Натуральная величина
отрезка прямой
В2
β
х
β-угол наклона прямой к
фронтальной плоскости
проекций
А2
В1
∆У
А1

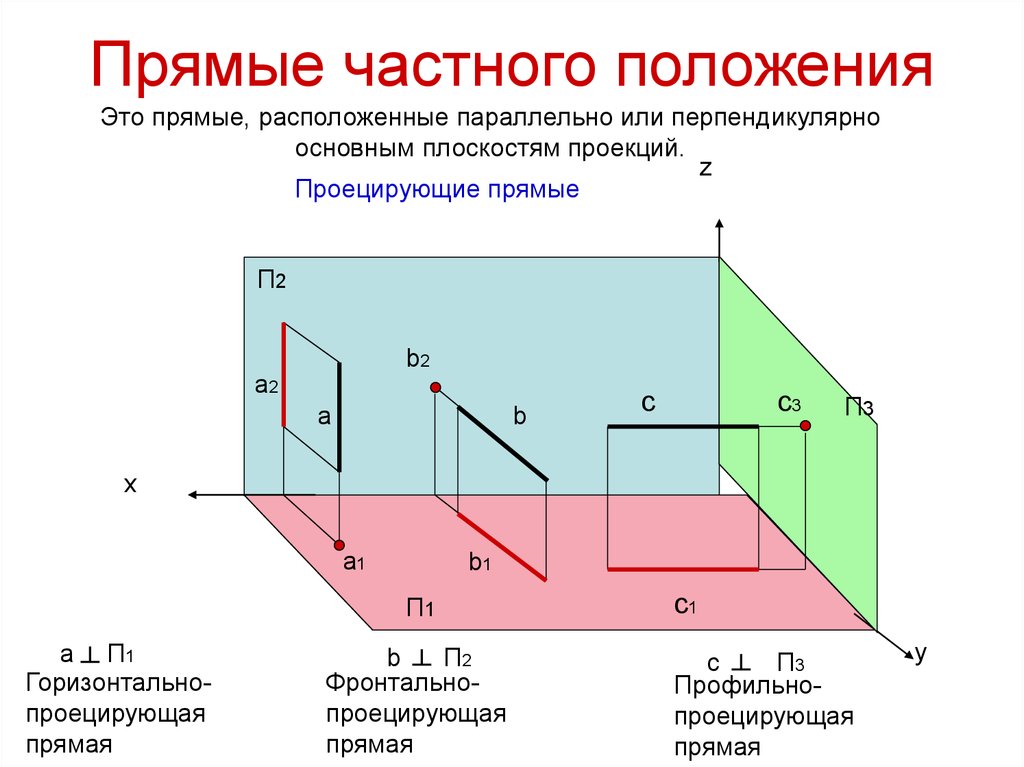
11. Прямые частного положения

Это прямые, расположенные параллельно или перпендикулярно
основным плоскостям проекций.
z
Проецирующие прямые
П2
b2
а2
а
b
c
c3
П3
x
а1
b1
П1
а ┴ П1
Горизонтальнопроецирующая
прямая
b ┴ П2
Фронтальнопроецирующая
прямая
c1
c ┴ П3
Профильнопроецирующая
прямая
y

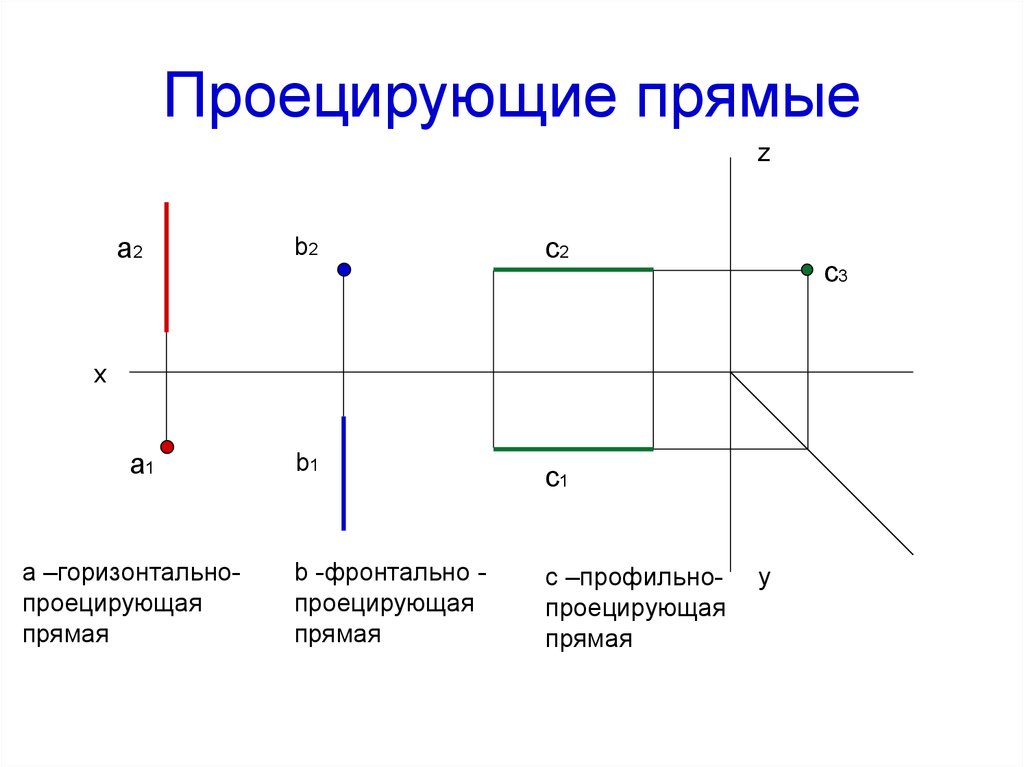
12. Проецирующие прямые

z
a2
b2
с2
b1
с1
b -фронтально проецирующая
прямая
с –профильнопроецирующая
прямая
с3
х
a1
а –горизонтальнопроецирующая
прямая
y

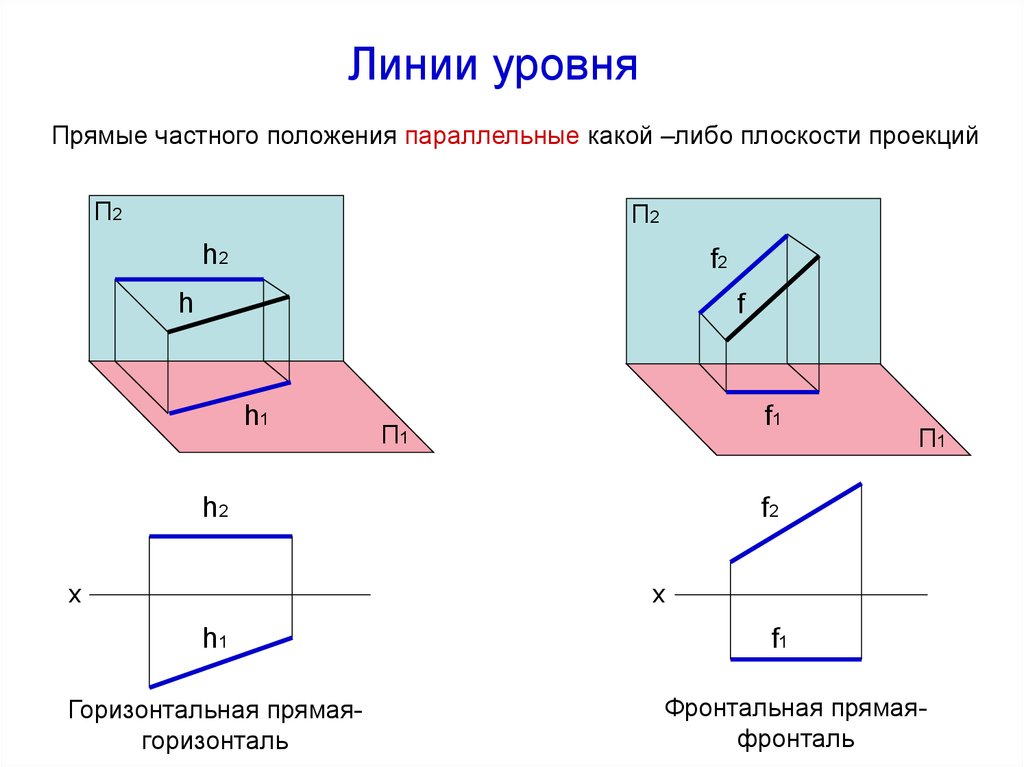
13. Линии уровня

Прямые частного положения параллельные какой –либо плоскости проекций
П2
П2
h2
f2
h
f
h1
f1
П1
h2
x
П1
f2
x
h1
Горизонтальная прямаягоризонталь
f1
Фронтальная прямаяфронталь

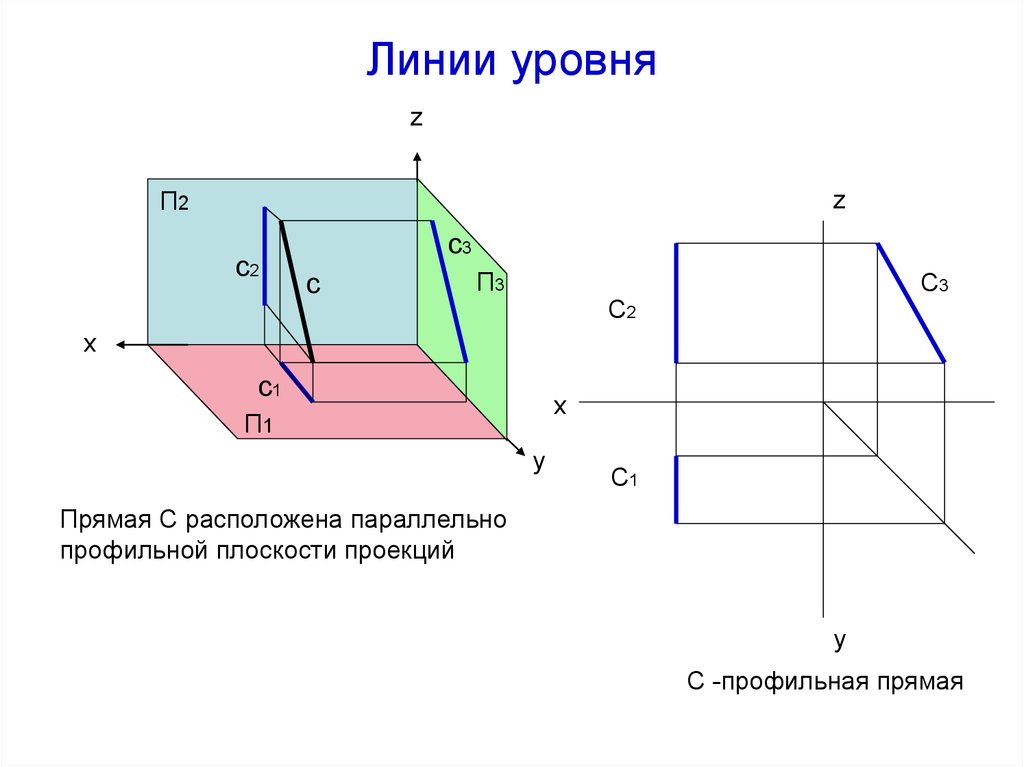
14. Линии уровня

z
П2
z
с2
с3
с
П3
C3
C2
x
с1
х
П1
y
C1
Прямая С расположена параллельно
профильной плоскости проекций
y
С -профильная прямая