Similar presentations:
Метрические задачи
1. Начертательная геометрия
Метрические задачиАвтор:Леонова О.Н.
2.
Метрические задачи-этозадачи на определение
расстояний ,углов и
истинных величин углов
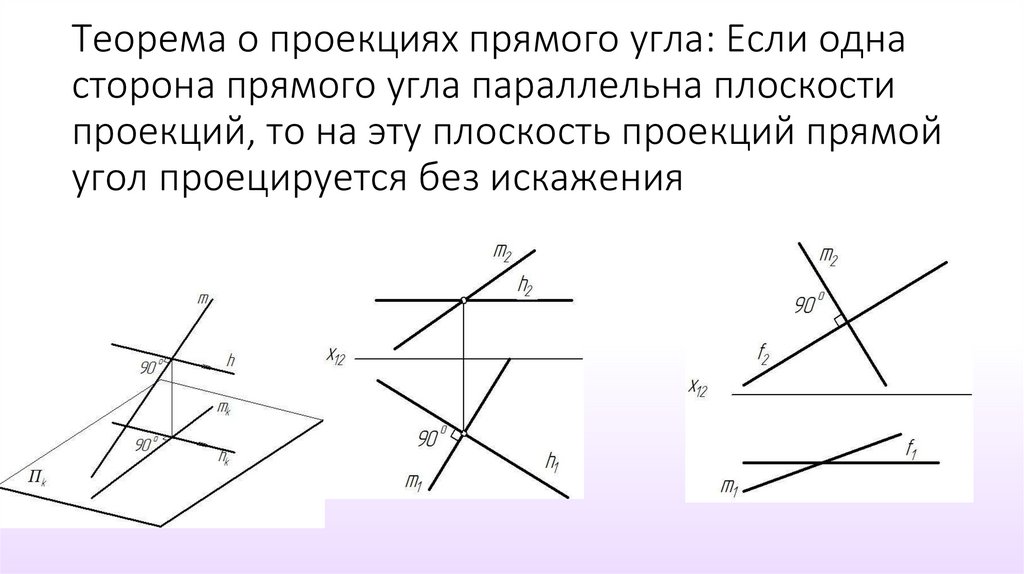
3. Теорема о проекциях прямого угла: Если одна сторона прямого угла параллельна плоскости проекций, то на эту плоскость проекций
прямойугол проецируется без искажения
4. Перпендикулярность прямой и плоскости Из геометрии известно, что прямая перпендикулярна плоскости, если она перпендикулярна
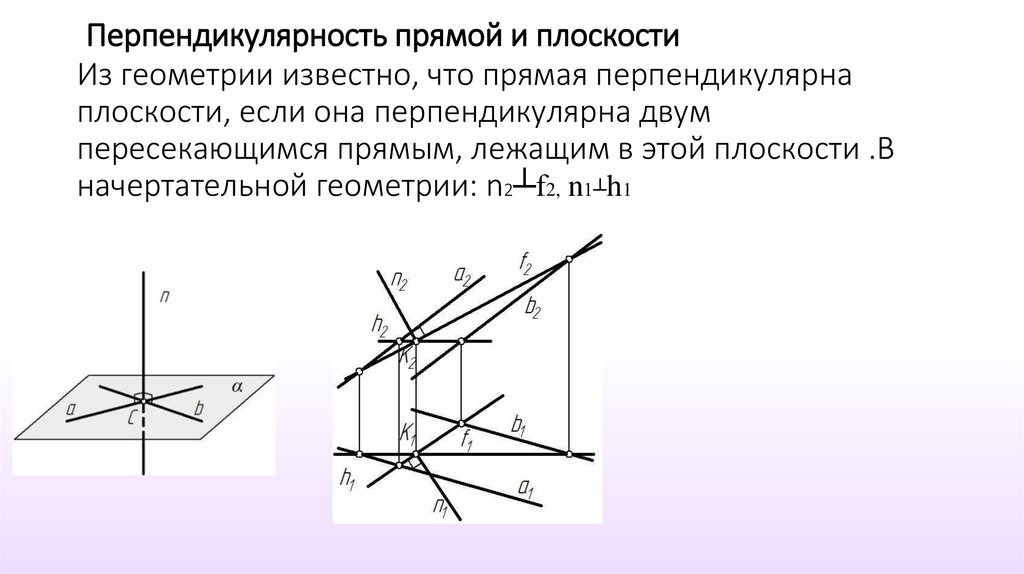
Перпендикулярность прямой и плоскостиИз геометрии известно, что прямая перпендикулярна
плоскости, если она перпендикулярна двум
пересекающимся прямым, лежащим в этой плоскости .В
начертательной геометрии: n2┴f2, n1┴h1
5.
Способы преобразования проекций применяют дляполучения нового изображения объекта или группы
объектов, которое позволяет упростить решение
поставленной задачи.
Как правило, это переход от общего положения к частному.
6.
Дополнительное прямоугольноепроецирование –
перемена плоскостей проекций
7.
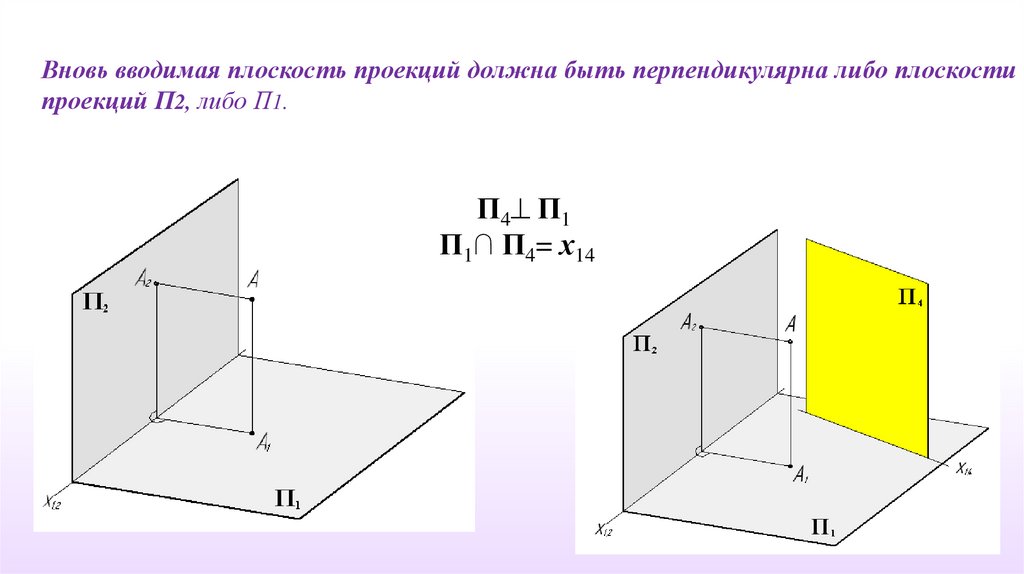
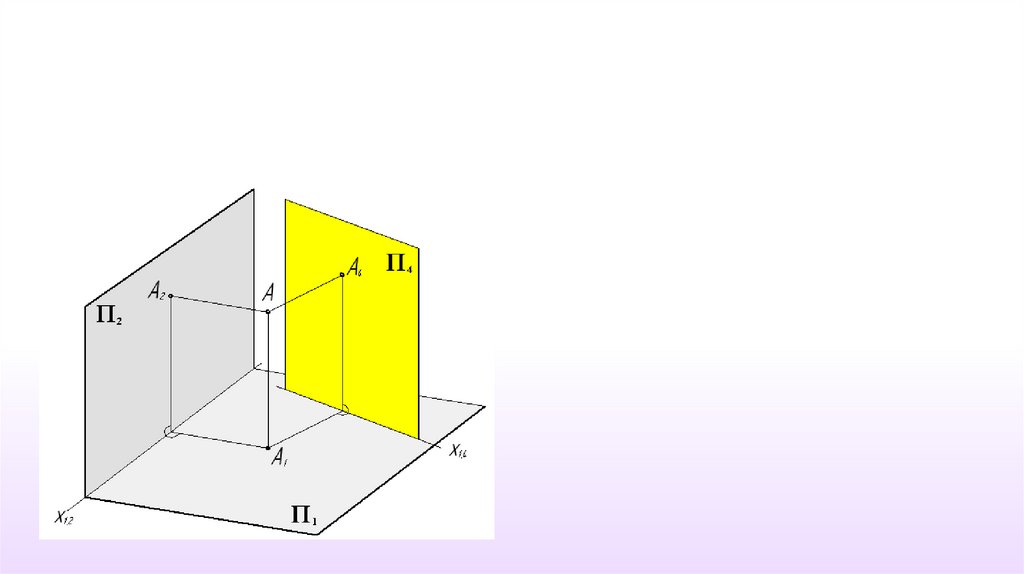
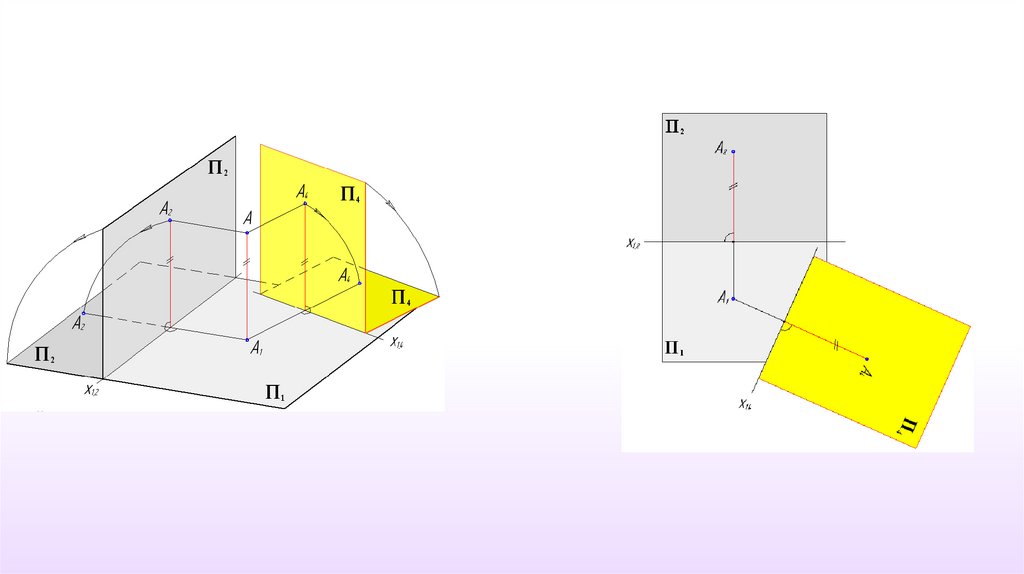
Вновь вводимая плоскость проекций должна быть перпендикулярна либо плоскостипроекций П2, либо П1.
П4 П1
П1∩ П4= х14
8.
9.
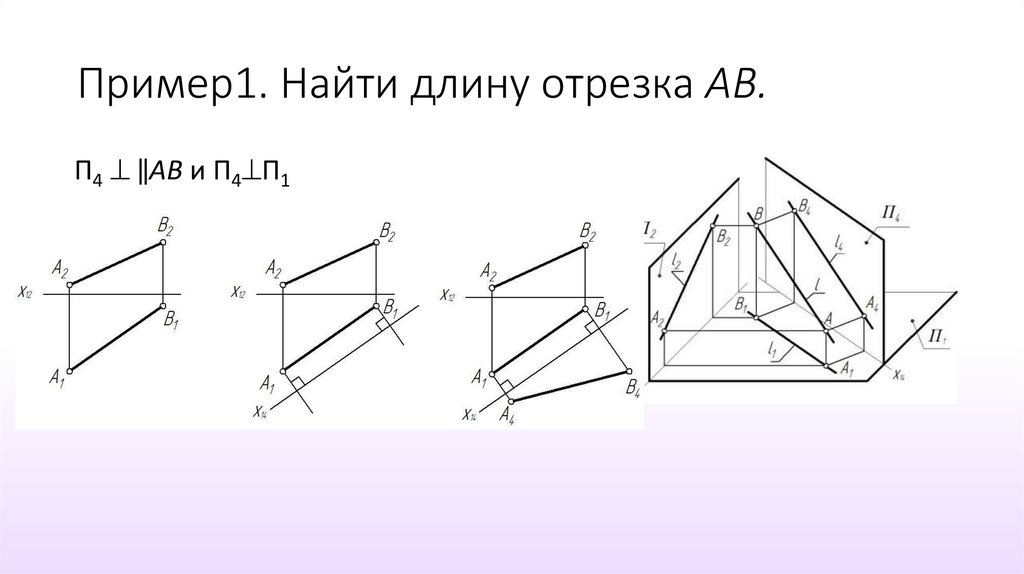
10. Пример1. Найти длину отрезка АВ.
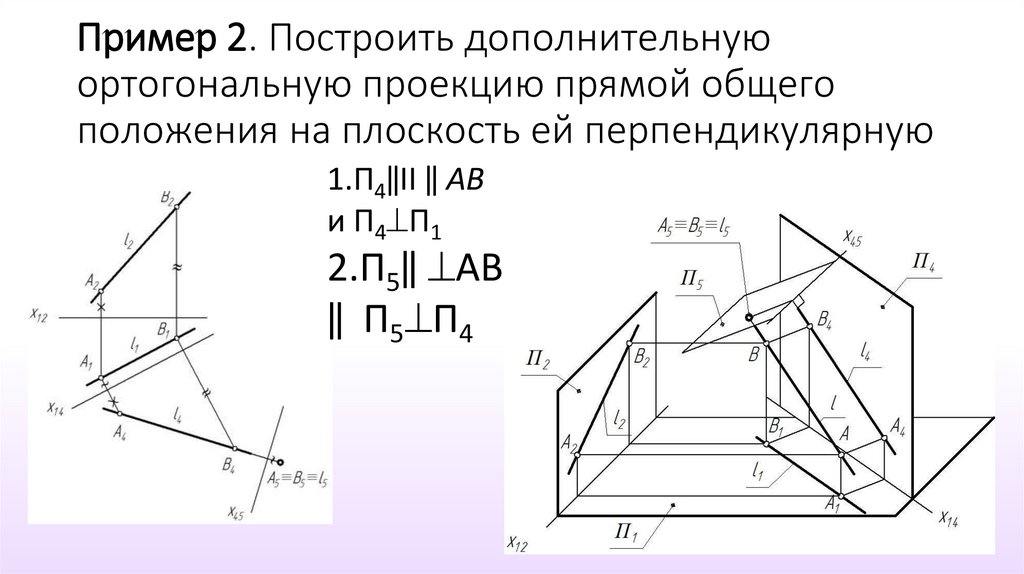
П4 ‖АВ и П4 П111. Пример 2. Построить дополнительную ортогональную проекцию прямой общего положения на плоскость ей перпендикулярную
1.П4‖II ‖ АВи П4 П1
2.П5‖ АВ
‖ П5 П4
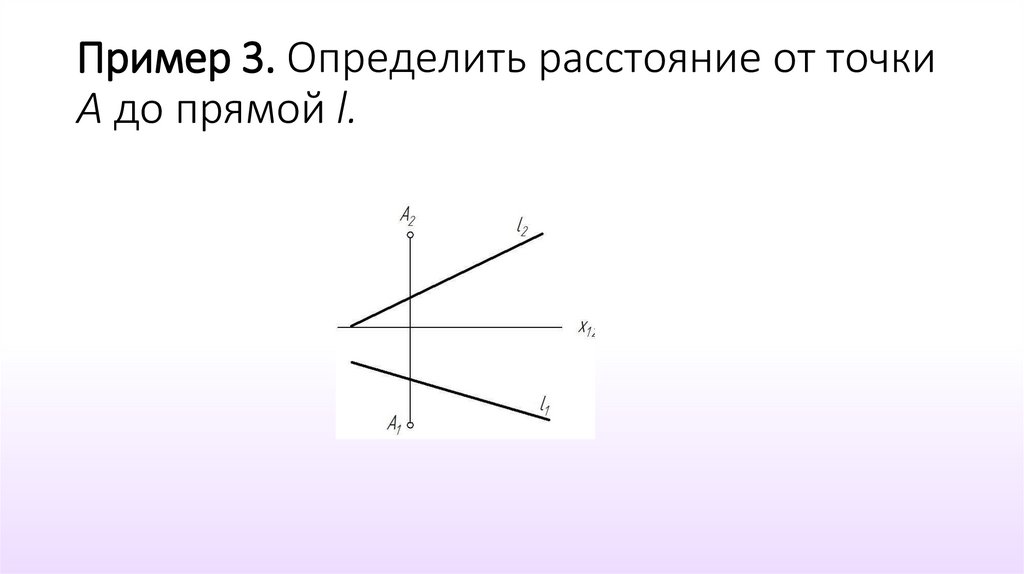
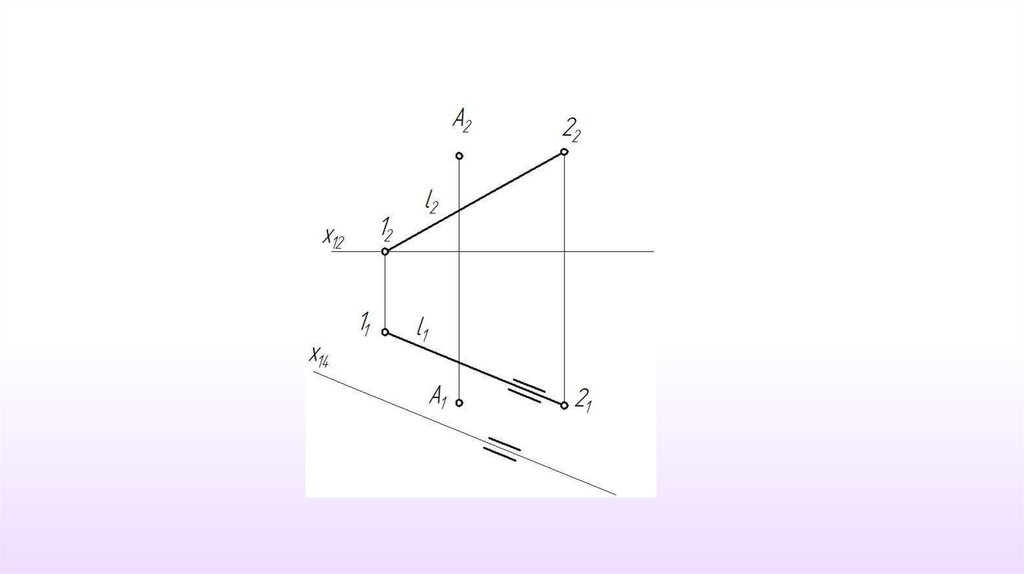
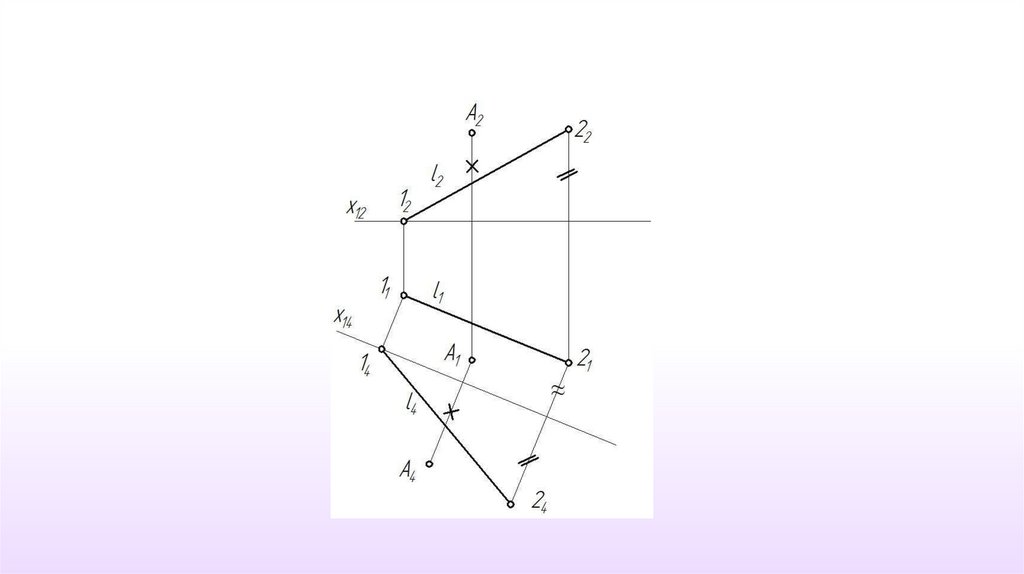
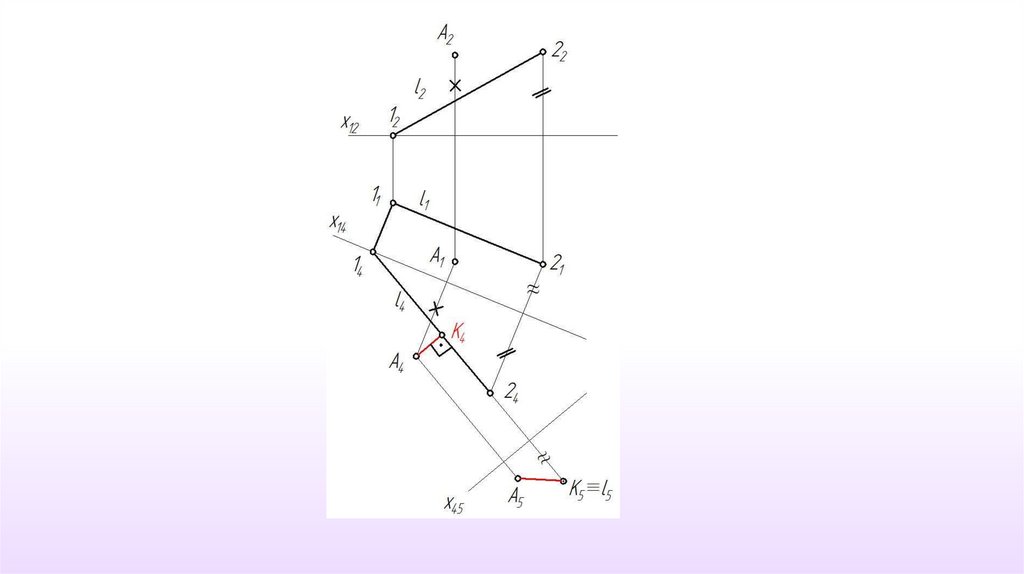
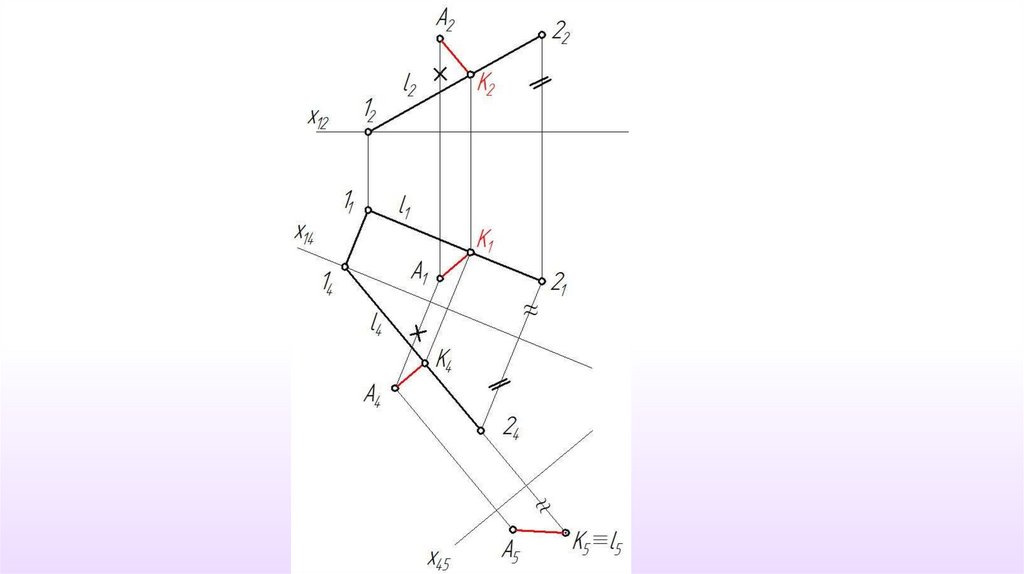
12. Пример 3. Определить расстояние от точки А до прямой l.
13.
14.
15.
16.
17.
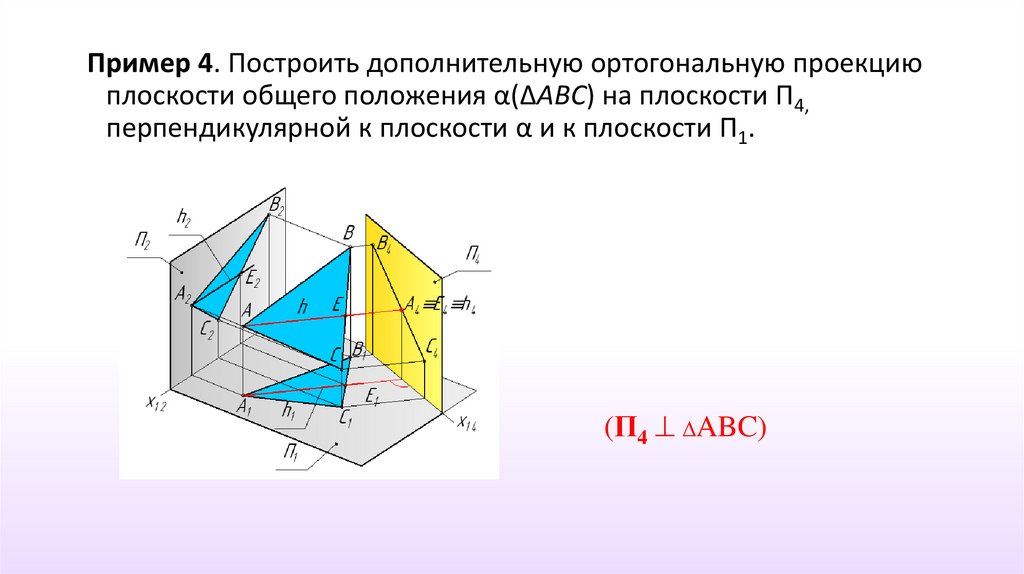
Пример 4. Построить дополнительную ортогональную проекциюплоскости общего положения α(ΔАВС) на плоскости П4,
перпендикулярной к плоскости α и к плоскости П1.
(П4 ΔABC)
18.
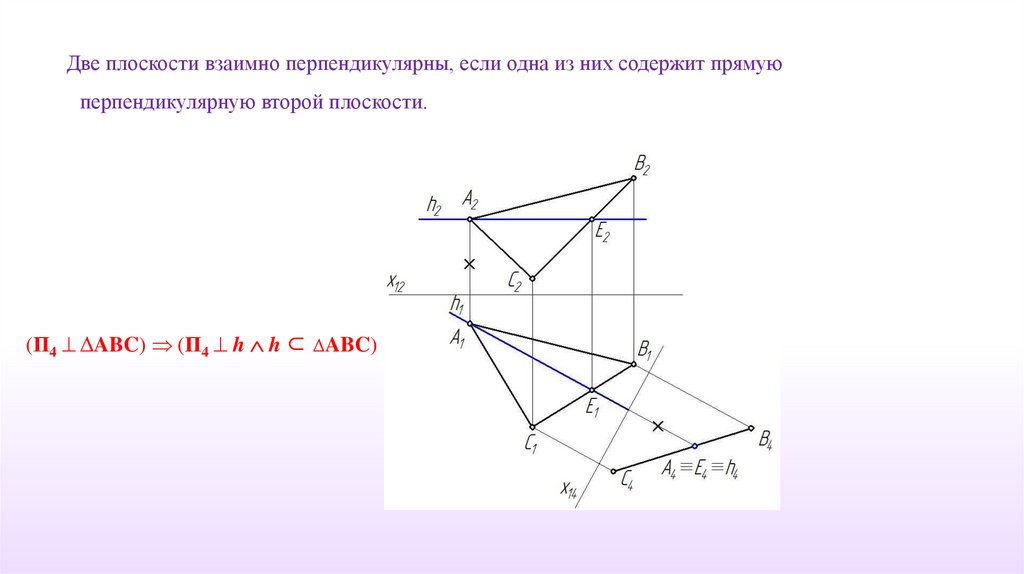
Две плоскости взаимно перпендикулярны, если одна из них содержит прямуюперпендикулярную второй плоскости.
(П4 ΔABC) (П4 h h ⊂ ΔABC)
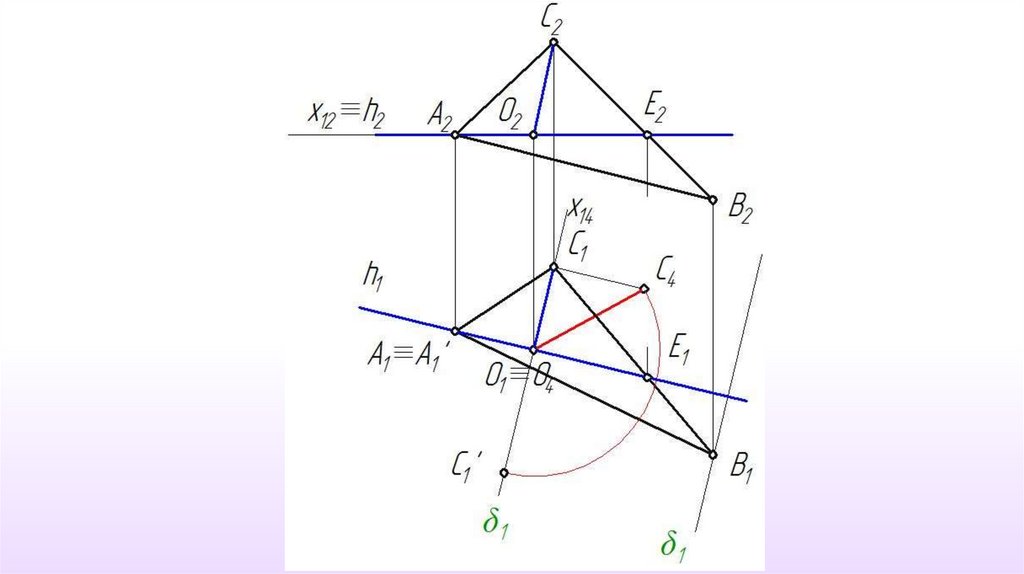
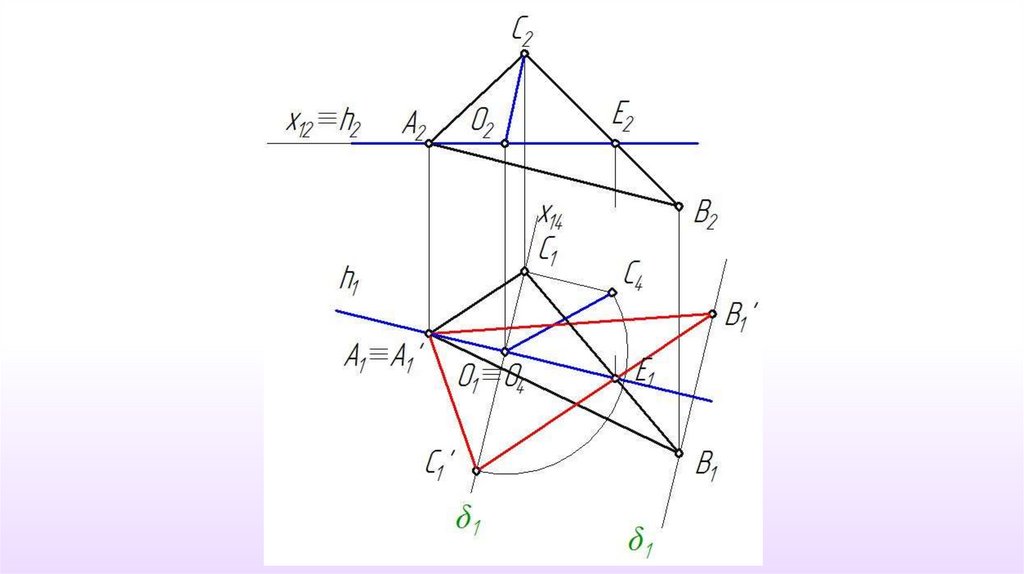
19. Пример 5 . Определить размеры треугольника АВС
1-й этап.П4 АВС
П4 П1 П4 h х14 h1
2-й этап.
П5 II АВС
П5 П4 х45 ‖ А 4В 4С4
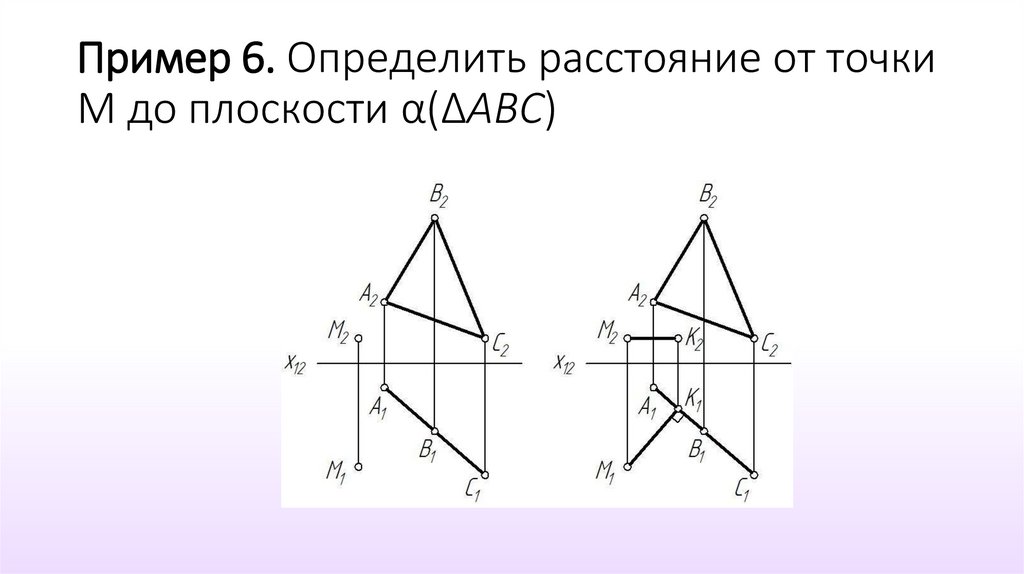
20. Пример 6. Определить расстояние от точки М до плоскости α(ΔАВС)
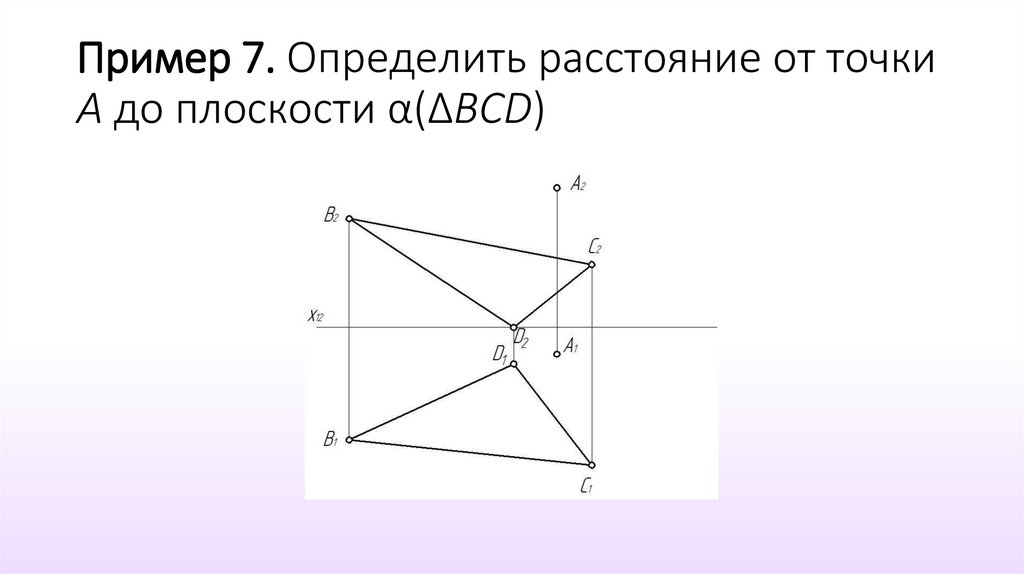
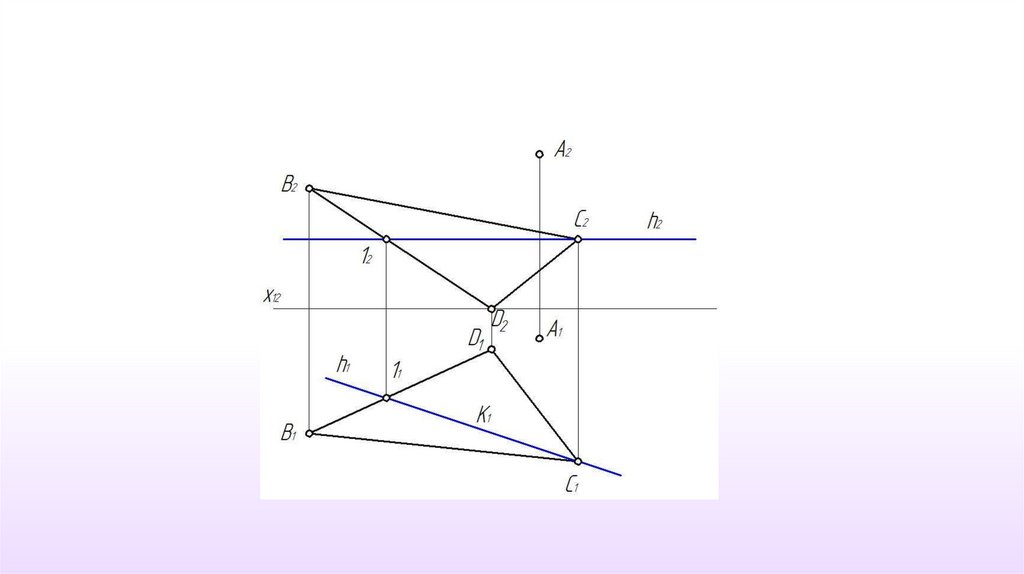
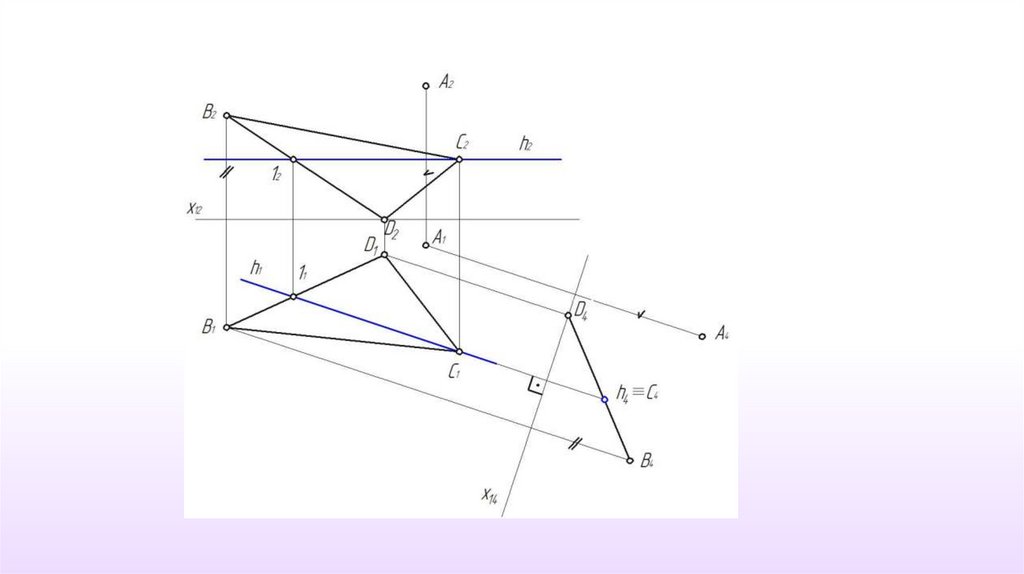
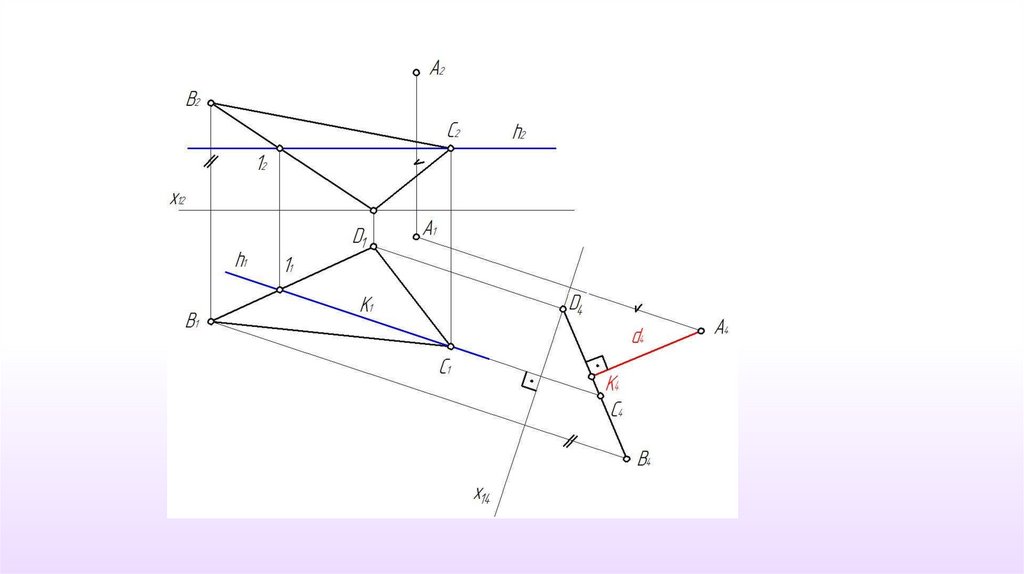
21. Пример 7. Определить расстояние от точки А до плоскости α(ΔВСD)
22.
23.
24.
25.
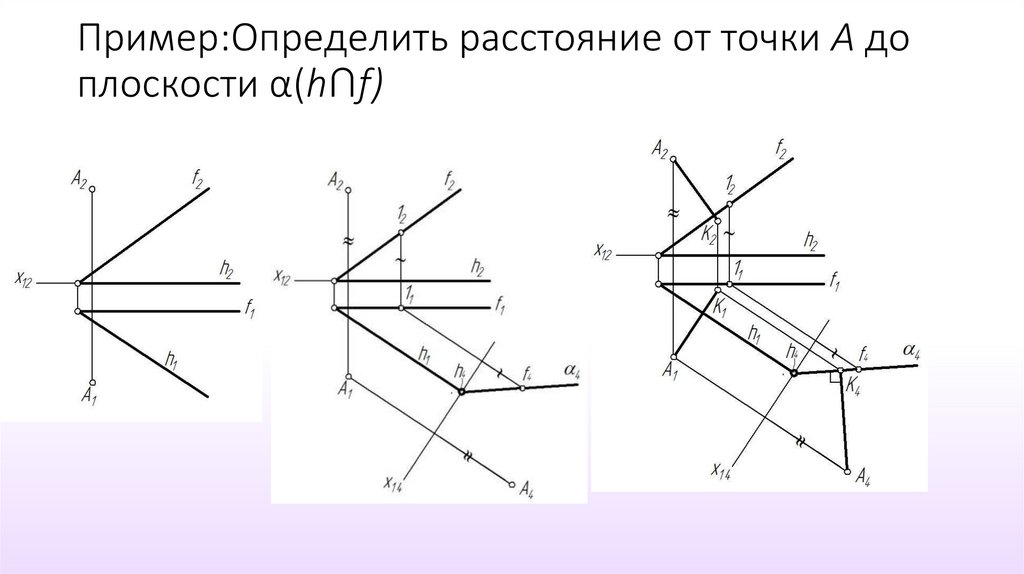
26. Пример:Определить расстояние от точки А до плоскости α(h∩f)
27.
..
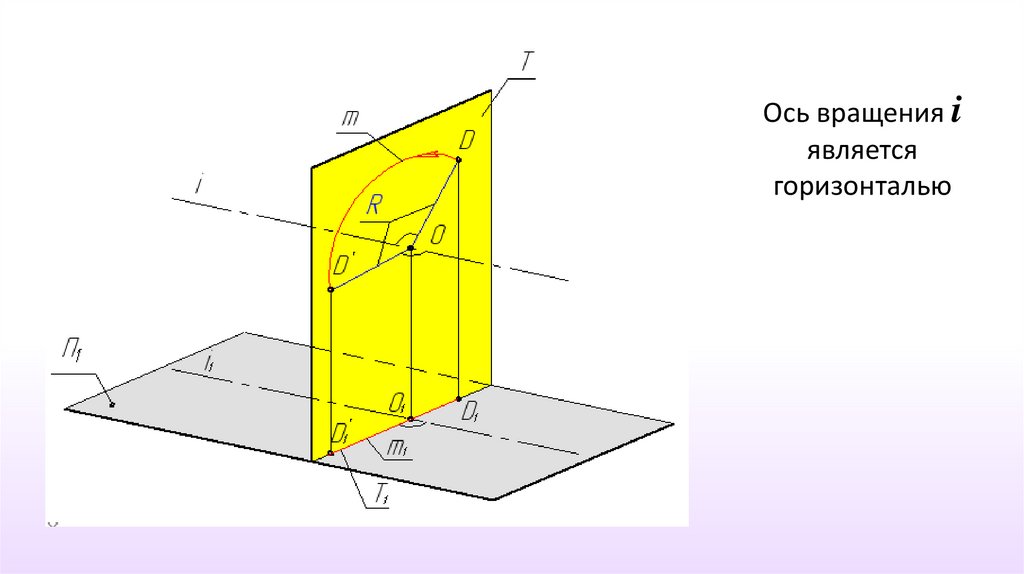
Вращение вокруг горизонтали
или фронтали
28.
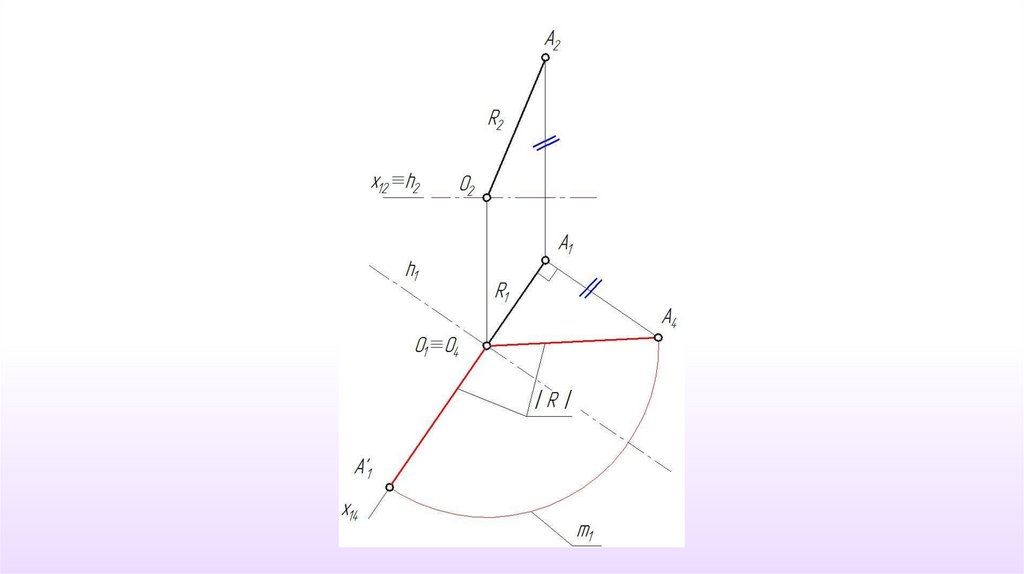
Ось вращения iявляется
горизонталью
29.
30.
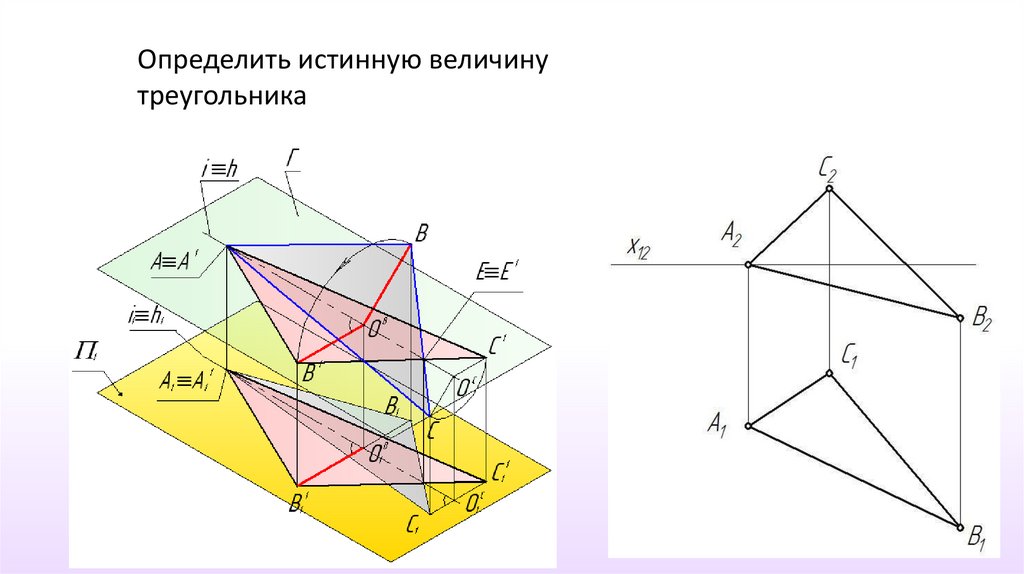
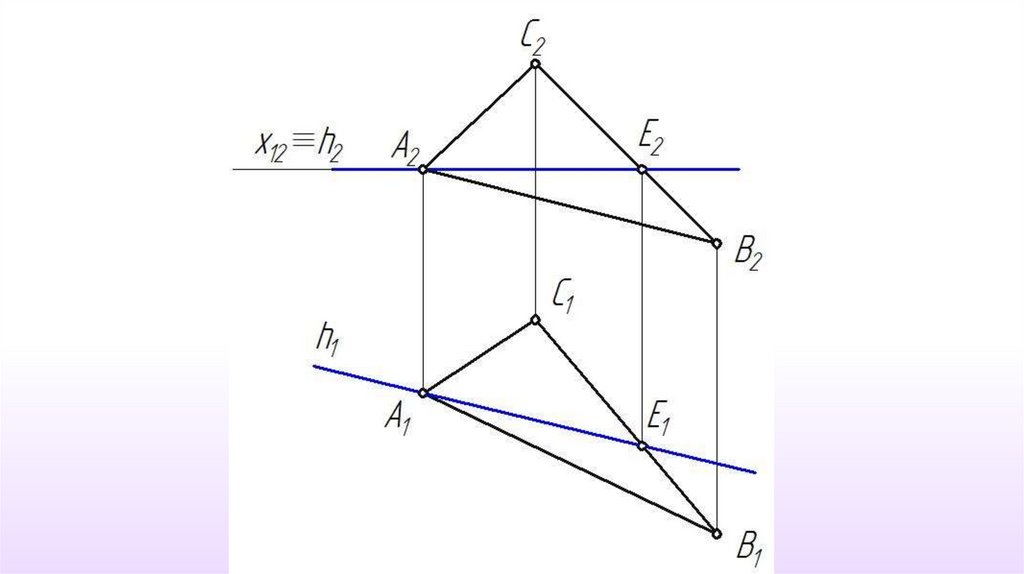
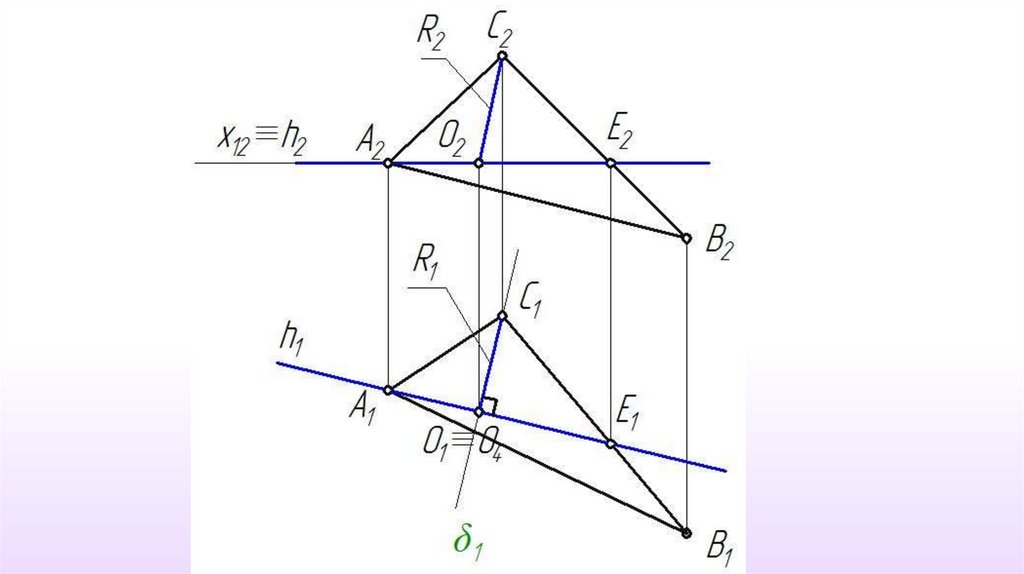
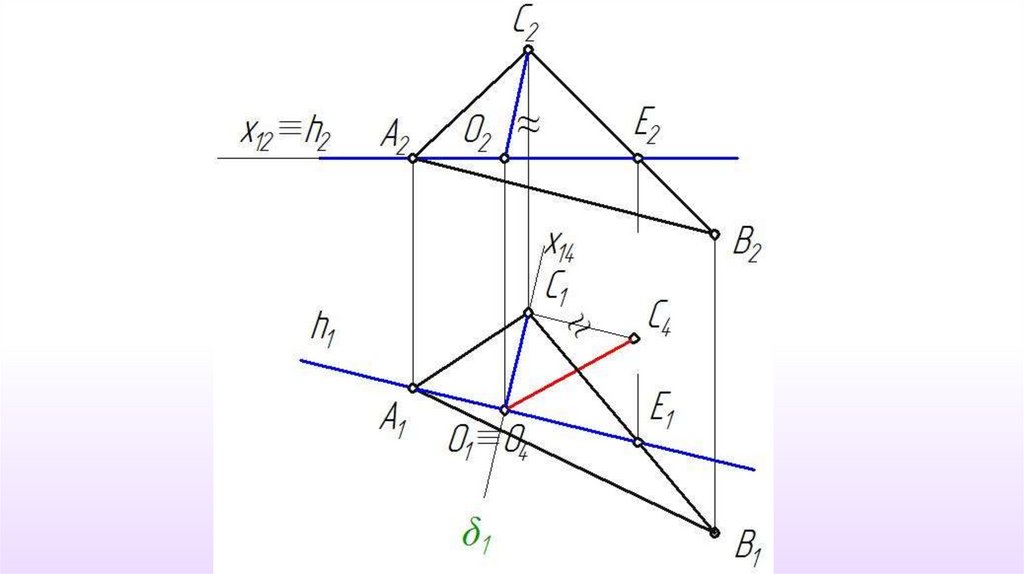
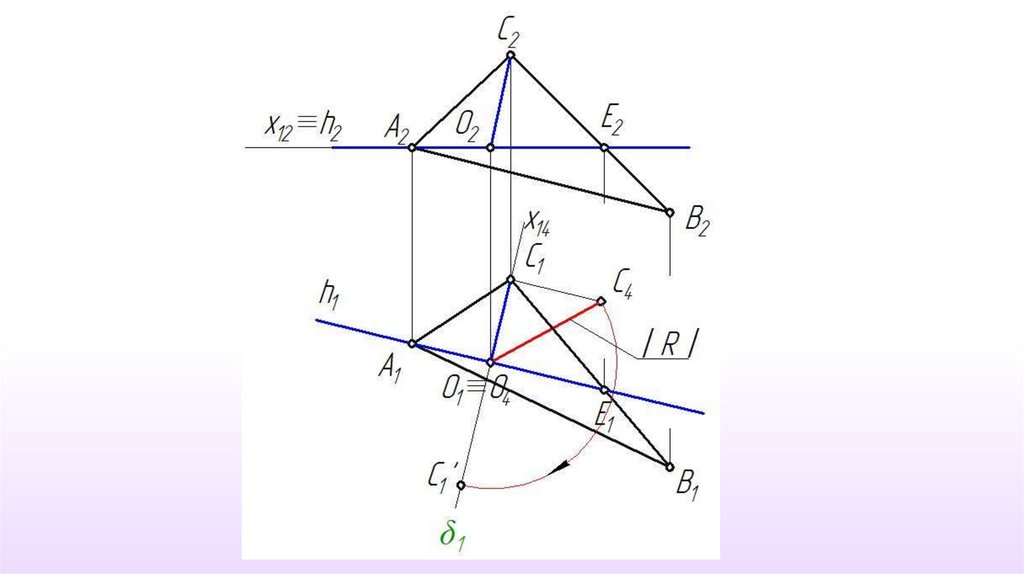
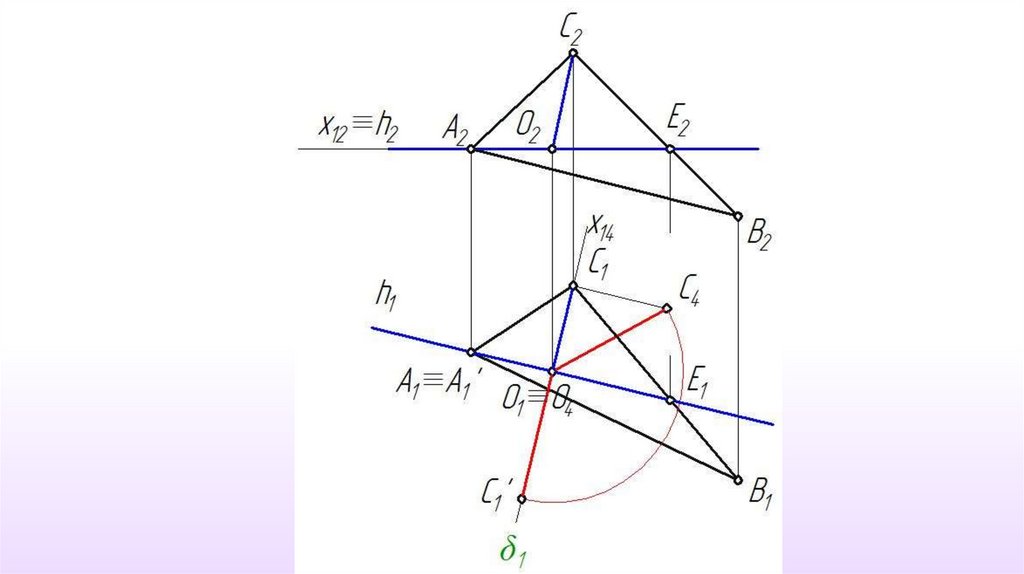
Определить истинную величинутреугольника
31.
32.
33.
34.
35.
36.
37.
38.
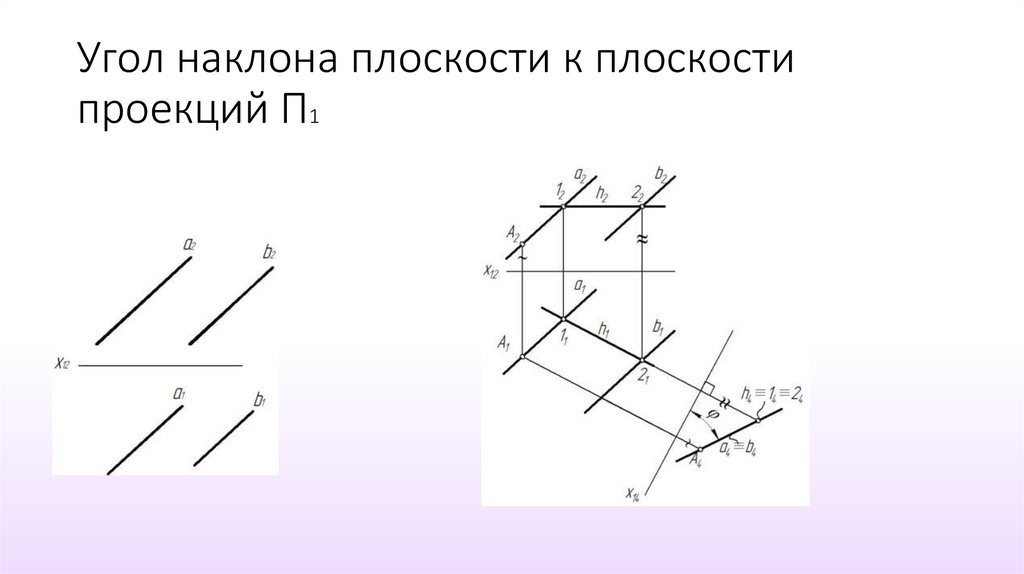
39. Определение углов
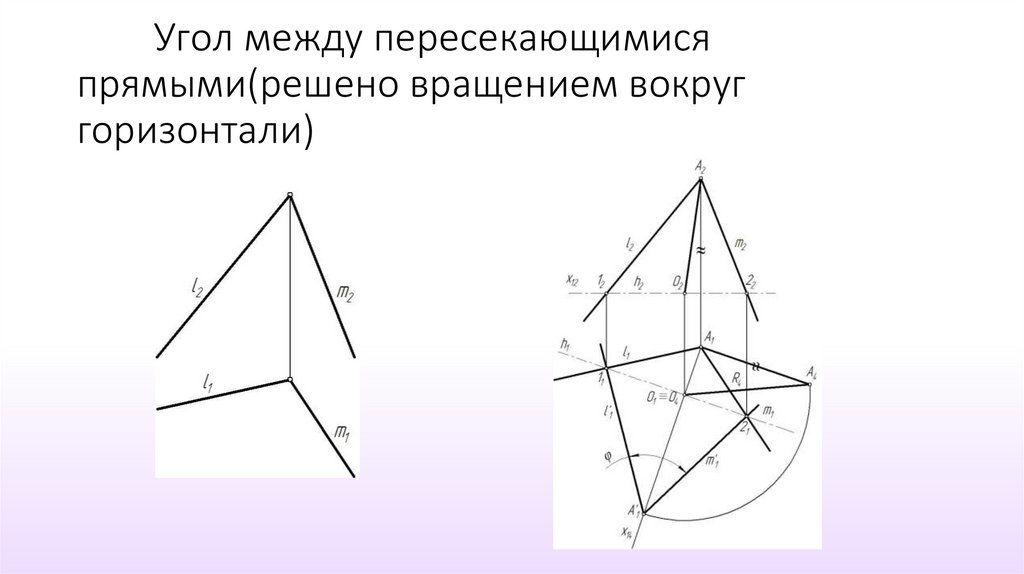
40. Угол между пересекающимися прямыми(решено вращением вокруг горизонтали)
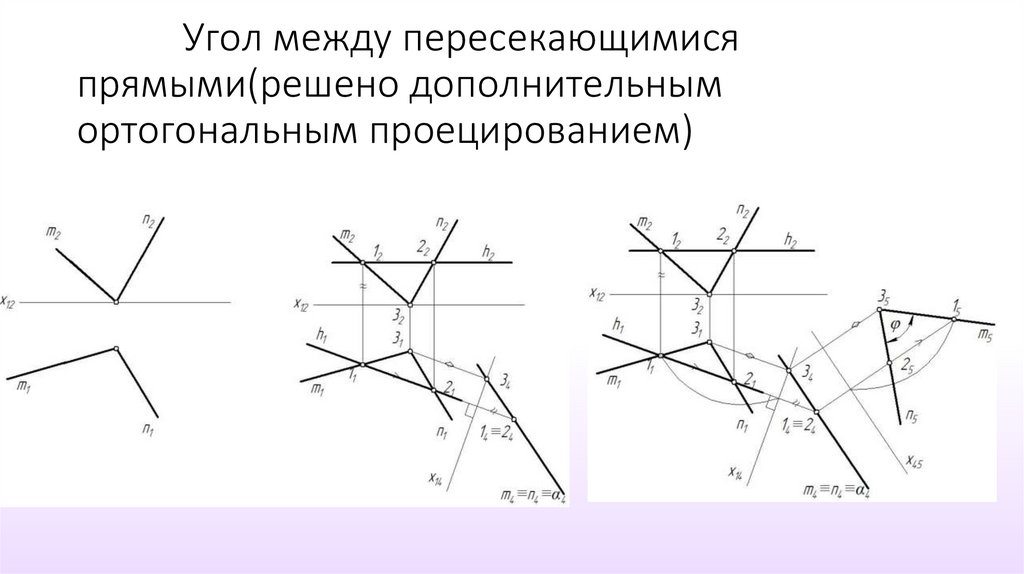
41. Угол между пересекающимися прямыми(решено дополнительным ортогональным проецированием)
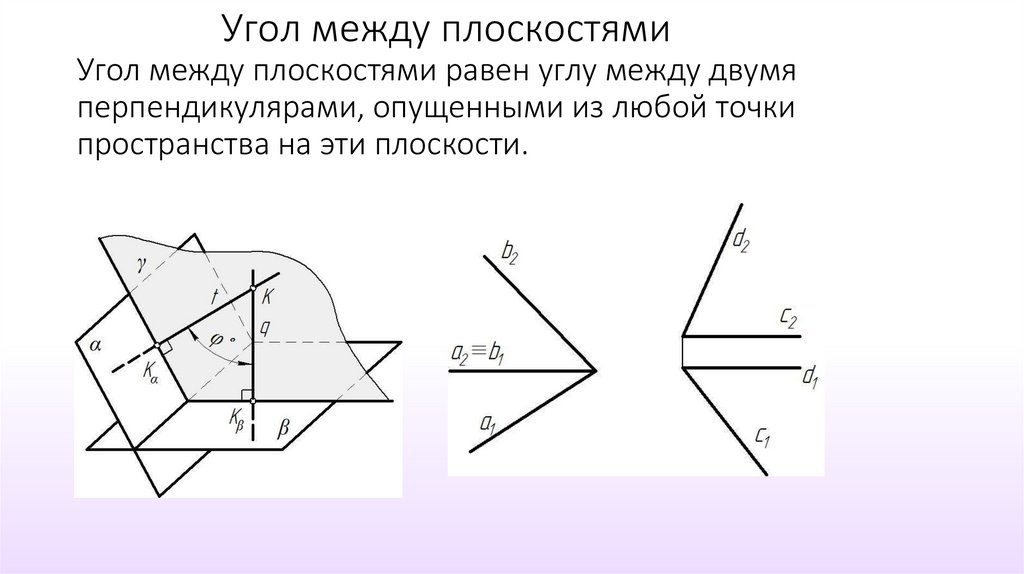
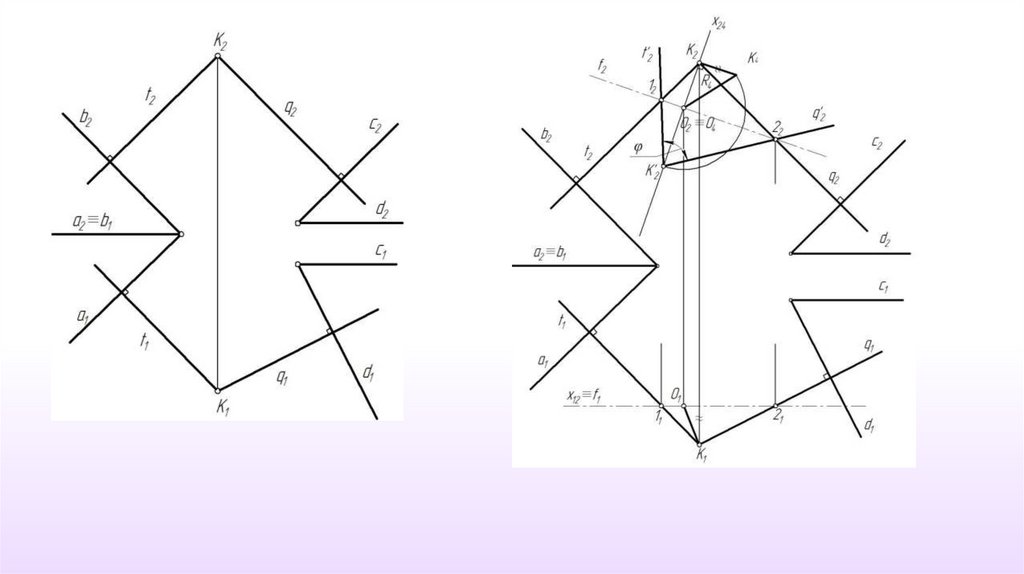
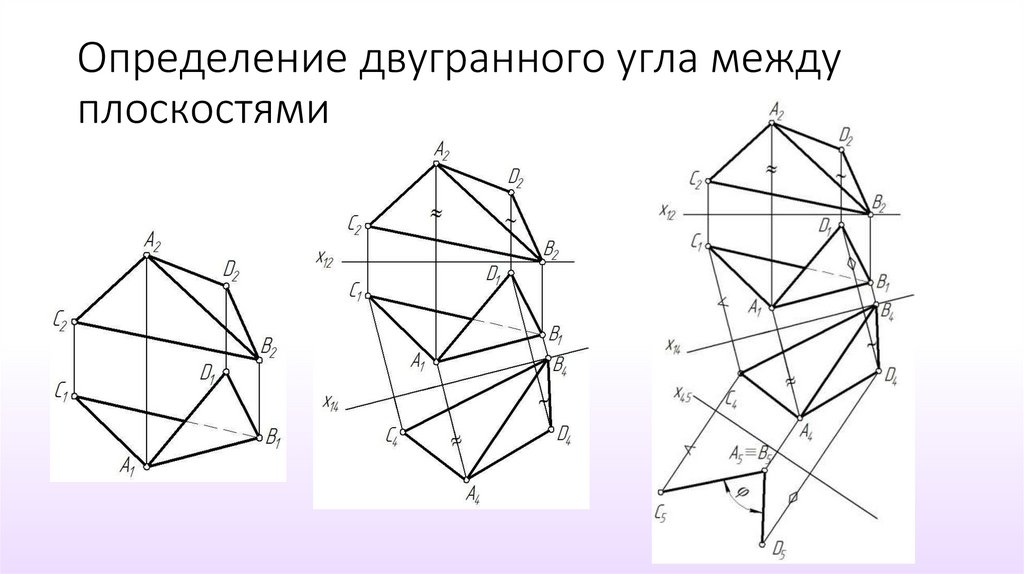
42. Угол между плоскостями Угол между плоскостями равен углу между двумя перпендикулярами, опущенными из любой точки пространства
на эти плоскости.43.
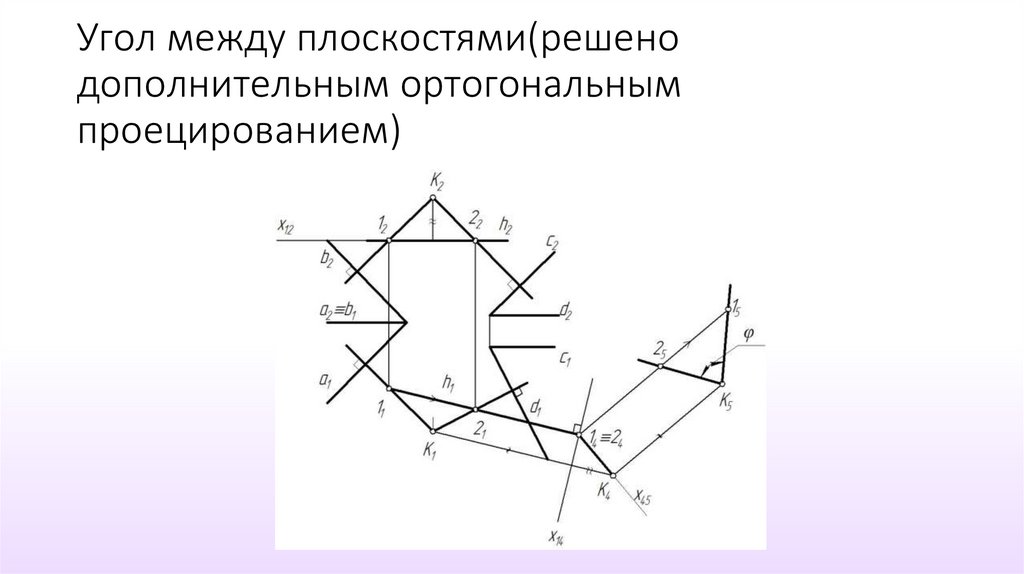
44. Угол между плоскостями(решено дополнительным ортогональным проецированием)
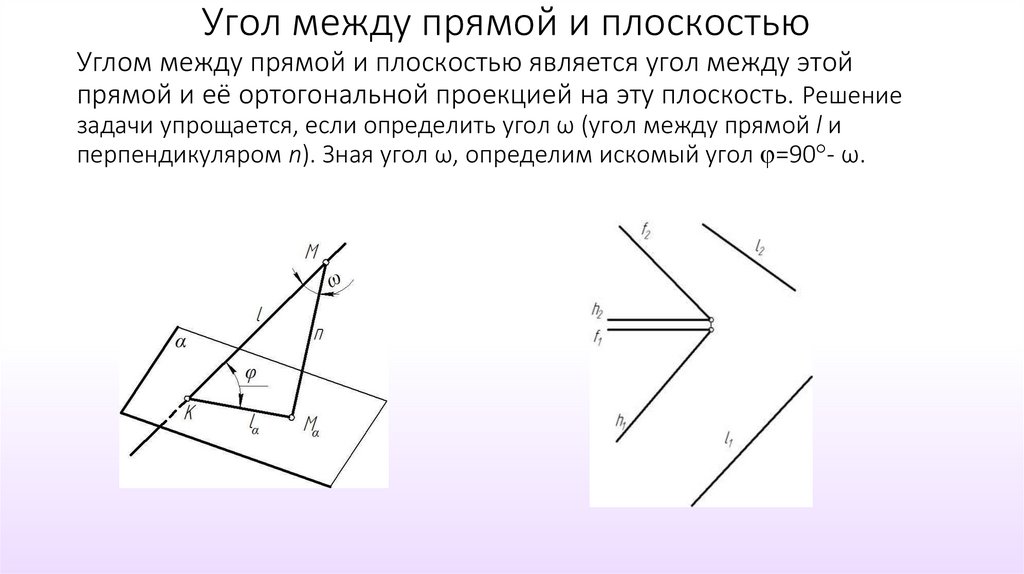
45. Угол между прямой и плоскостью Углом между прямой и плоскостью является угол между этой прямой и её ортогональной проекцией на
эту плоскость. Решениезадачи упрощается, если определить угол ω (угол между прямой l и
перпендикуляром n). Зная угол ω, определим искомый угол =90 - ω.










 drafting
drafting








