Логарифмические неравенства

1.

2. Девиз урока:

Дорогу осилит идущий,
а математику - мыслящий.

3. Тема урока:

Решение
логарифмических
неравенств

4. Цель:

Закрепление и систематизация знаний о
логарифмических неравенствах
Задачи:
Отработать навыки решения логарифмических
неравенств;
Рассмотреть типичные трудности, встречающиеся при
решении логарифмических неравенств;
Показать связь математики с другими науками.

5.

ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ
1. Дать определение логарифмической
2.
3.
4.
5.
6.
7.
y=loga x, a>1.
функции
Область определения.
Множество значений.
Четность, нечетность.
Возрастание, убывание.
Нули функции.
Промежутки знакопостоянства.

6. Устные упражнения

7.

Задание 1. Найдите область
определения функции.
;

8.

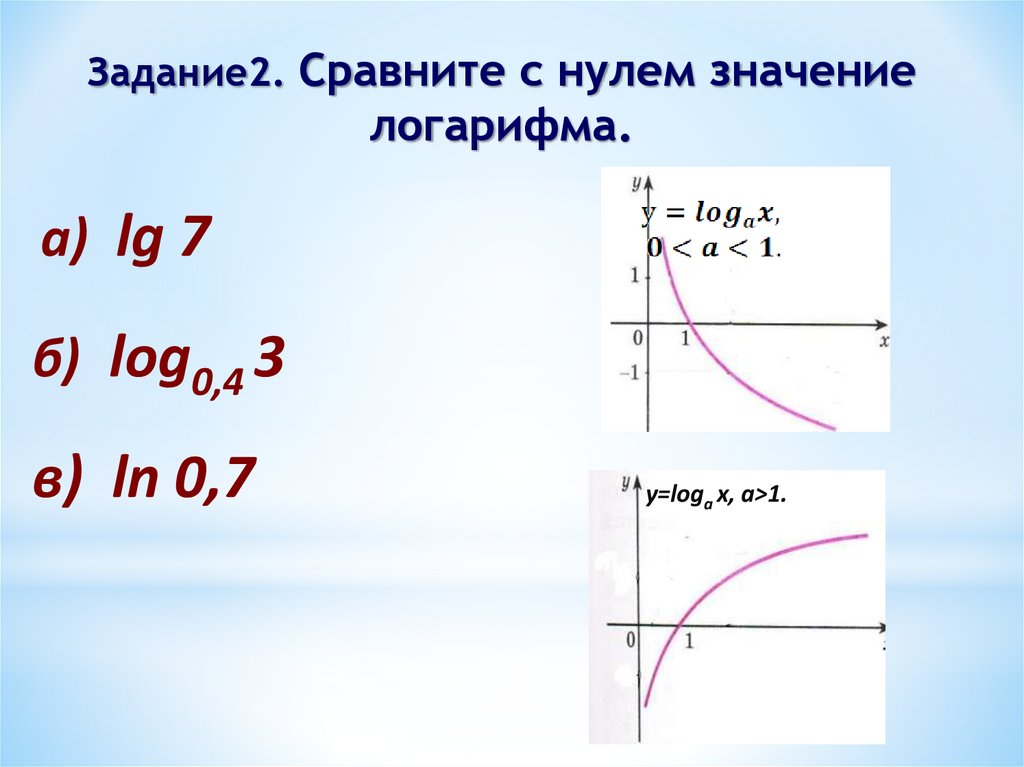
Задание2. Сравните с нулем значение
логарифма.
а) lg 7
б) log0,4 3
в) ln 0,7
y=loga x, a>1.

9.

Задание 3. Решите неравенство:
а) log0,3 x > log0,3 5;
б) logx6 < logx3;
В) (х-5) log0,54< 0;

10.

Софизм – это рассуждение,
кажущееся правильным, но
содержащее скрытую
логическую ошибку.

11.

,
Логарифмический софизм: 2>3.
,
,

12.

Методы решения неравенств
1. Сведение неравенства к равносильной
системе или совокупности систем
2. Расщепление неравенств
3. Метод перебора
4. Метод интервалов
5. Введение новой переменной
6. Метод рационализации
7. Использование свойств функции :
а) область определения;
б) ограниченность;
в) монотонность.

13.

Внимание!
1.ОДЗ исходного
неравенства.
2.Учитывать свойство
монотонности функции.

14.

РЕШИТЬ!
1 log 0,1 x 2 x 2 log 0,1 x 3 .
2
3
log 2 3 x 2
0.
log 2 2 x 3
x2 4
0.
2
log 1 x 1
2
4
25 х 30 5 х 125 0,
log х ( х 1) log х ( х 1) 0.
5
Без помощи калькулятора сравните
числа
log43 и log32

15.

Правильному применению
методов можно научиться, только
применяя их на различных
примерах.
Цейтен

16. Решение неравенств

lg( 2 x 4 x 10) lg( x 4 x 3)
2
2
log x 2 (2 x 3) log x 2 (24 6 x)
2x2 4x 6
log 1/ 2
1
4 x 11
log 0,3 ( x3 8) log 0,3 ( x 2 4 x 4) log 0,3 ( x 58)
log 2 2 ( x 1)2 5 log 0,5 ( x 1) 1

17.

Самостоятельная работа
2 Вариант
1 Вариант
Внимание!
1.ОДЗ исходного
неравенства.
2.Учитывать свойство
монотонности функции.

18.

Самостоятельная работа
проверка
2 Вариант
1 Вариант
Решение:
Ответ:
Решение:
.

19.

Найди ошибку.
1. а)log8 (5х-10) < log8(14-х),
5x-10 < 14-x,
6x < 24,
x < 4.
Ответ: х € (-∞; 4).
Ошибка: не учли область определения неравенства.
Верное решение:
log8 (5х-10)< log8(14-х)
Ответ: х € (2;4).
2<x <4.

20.

Ошибка: не учтена область определения исходного
неравенства.
Верное решение:
Ответ: х

21.

ЛАБОРАТОРИЯ ХИМИИ.
Задача. Рассчитать температурный
коэффициент химической реакции
в технологии производства
оптоволокна. Он равен
наибольшему целому решению
неравенства
Ответ:3.

22.

ЛАБОРАТОРИЯ ФИЗИКИ.
Задание. Найти период полураспада
β – частицы в процессе движения по
траектории светоизлучения. Он
равен наибольшему целому решению
неравенства
Ответ: 2 .

23. Цель:

Закрепление и систематизация знаний о
логарифмических неравенствах
Задачи:
Отработать навыки решения логарифмических
неравенств;
Рассмотреть типичные трудности, встречающиеся при
решении логарифмических неравенств;
Показать связь математики с другими науками.

24. Задание:

x 5 2
log 5 (
) 0
x
2 2x 3
lg( x 1 1)
3
3
lg x 40