Similar presentations:
Решение логарифмических неравенств. Формирование знаний
1.
Решение логарифмическихнеравенств
2. Цель урока:
Формирование знаний по теме«Логарифмические неравенства»
3. Задачи урока:
1. Ввести понятие логарифмическогонеравенства.
2. Рассмотреть и систематизировать
методы решения логарифмических
неравенств.
3. Сформировать умения применять
теоретические знания при решении
неравенств.
4.
Найдите область определения функций:а)
;
Повторение
б)
;
в)
;
г)
;
д)
.
5.
Логарифмическим неравенствомназывается неравенство, в котором
переменная находится под знаком
логарифма
6.
Логарифмическими неравенствами называютнеравенства вида
и неравенства, сводящиеся к этому виду
7.
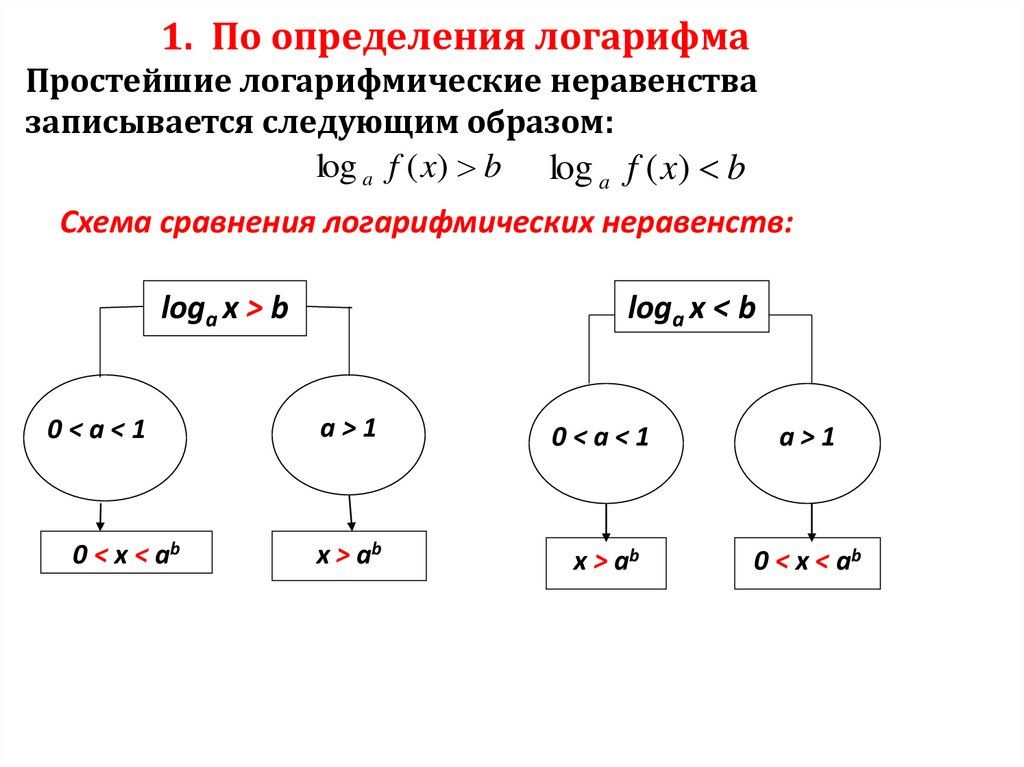
1. По определения логарифмаПростейшие логарифмические неравенства
записывается следующим образом:
log a f ( x) b log a f ( x) b
Схема сравнения логарифмических неравенств:
logа x > b
0<a<1
0 < x < ab
logа x < b
a>1
0<a<1
a>1
x > ab
x > ab
0 < x < ab
8.
Ответ : (3; )9.
+-
+
-1
+
4
1
1
-
2
2
х
+
х
Ответ : [ 1;1) (2;4].
10.
2. Метод потенцированияСуть метода в следующем: с помощью формул
неравенство привести к виду log a f ( x) log a g ( x)
Справедливы следующие утверждения:
f ( x) g ( x),
log a f ( x) log a g ( x) f ( x) 0, a 1
g ( x) 0;
f ( x) g ( x),
log a f ( x) log a g ( x) f ( x) 0, 0 a 1
g ( x) 0;
11.
1) log 5 (2 x) log 5 ( x 1)Т .к. 5 1, то функция у log 5 t возрастающая
и, учитывая ОДЗ , получаем
2 х х 1
х 1
х 1
х 1 0
х 1
Ответ : (1; )
12.
2) log 1 (2 x) log 1 ( x 1)2
2
1
Т .к. 0 1, то функция у log 1 t убывающая
2
2
и, учитывая ОДЗ , получаем
2 х х 1
х 1
решений нет
2 х 0
х 0
Ответ : решений нет
13.
3).14.
15.
4).16.
5).17.
В парах :log 1 ( x 2) log 1 4 х
3
3
18.
log 1 ( x 2) log 1 4 х3
3
х 2 0,
4 x 0,
x 2 4 х;
х 2,
x 4,
x 3;
3 x 4
Ответ : (3;4).
19.
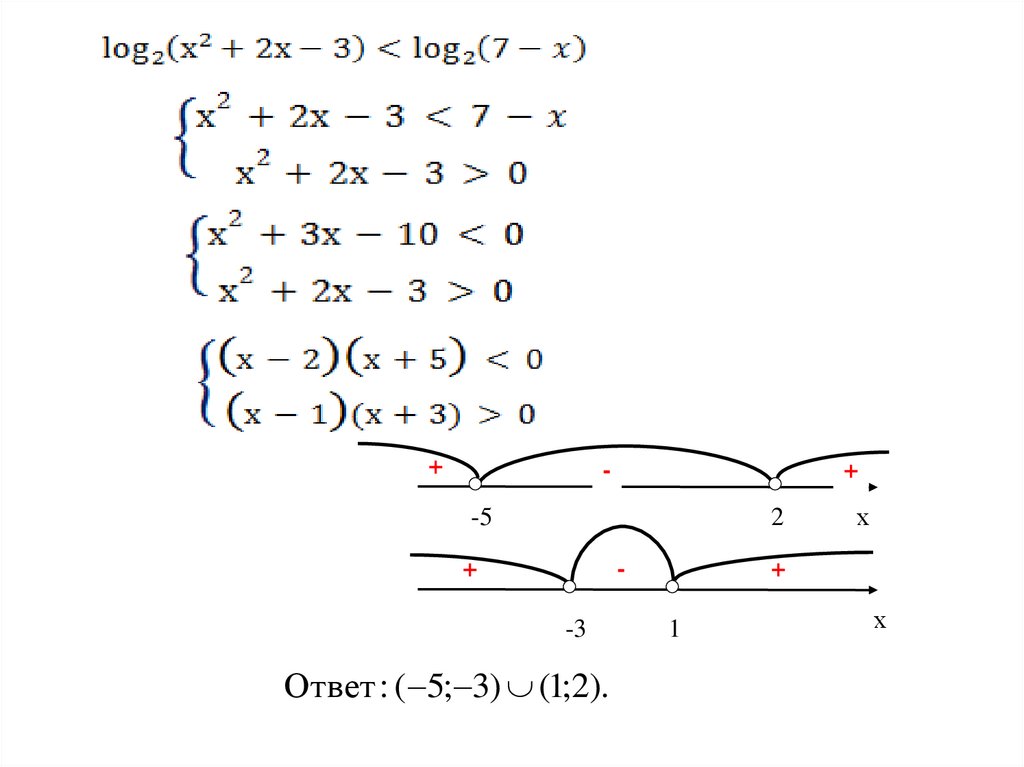
+-
+
-5
2
+
-3
Ответ : ( 5; 3) (1;2).
х
+
1
х
20.
Найдите ошибку:log8 (5х-10) < log8(14-х),
5x-10 < 14-x,
6x < 24,
x < 4.
Ответ: х (-∞; 4).
Ошибка: не учли область определения неравенства
Верное решение:
log8 (5х-10)< log8(14-х)
2<x <4.
Ответ: х (2;4).
21.
Устно:22.
23.
24.
3.Метод введения новой переменной:Ищем в неравенстве некоторое повторяющееся
выражение,
которое
обозначим
новой
переменной,
тем
самым,
упрощая
вид
неравенства
25.
3. Метод введения новой переменной:26.
27.
28.
29.
30.
Ответ : [0,6;13].31.
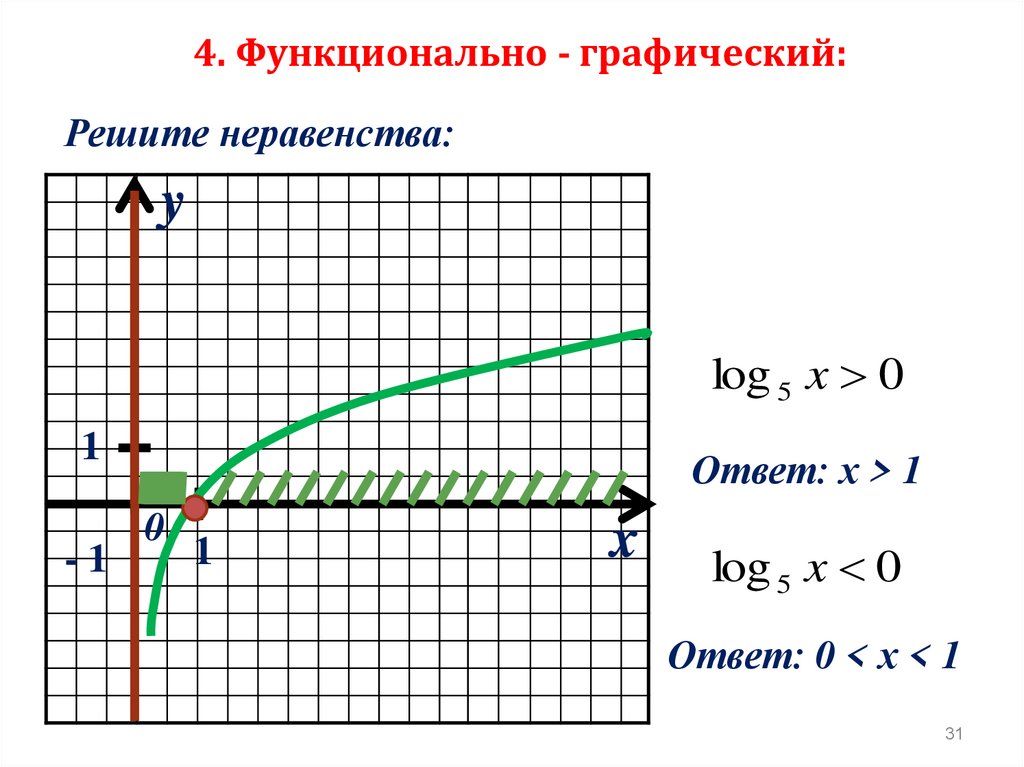
4. Функционально - графический:Решите неравенства:
y
log 5 x 0
1
-1
Ответ: х > 1
0
1
x
log 5 x 0
Ответ: 0 < х < 1
31
32.
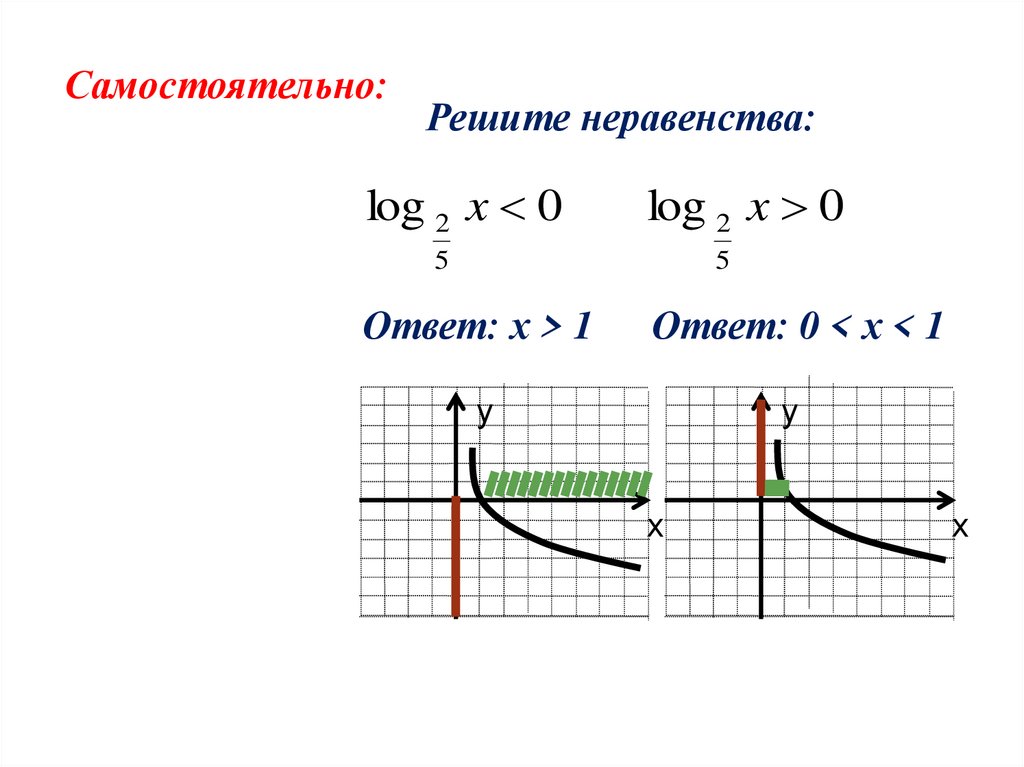
Самостоятельно:Решите неравенства:
log 2 x 0
log 2 x 0
5
5
Ответ: х > 1
Ответ: 0 < х < 1
у
у
х
х
33.
Физминутка для глаз34.
Решить самостоятельно1). log 1 х 4
3
2). log 1 (3x 3)
36
1
2
3). log ( x 2 4 x 3) 1
8
4). log 1 ( x 2 3 x 4) log 1 (8 x)
4
4
5). log 1 ( x 4) log 3 (4 х) 1
3
6). lg x lg x 6 0
2
7).2 log x log 1 (5 x) 2
2
5
5
35.
Ответы :1
1
.(
0
;
)
1б
81
1б 2.( 1;1]
1б 3. ; 1 5;
2б 4. ; 6 2;
2б 5. 2;4
3б 6. 0;0,01 100;
1, 5
7
.
0
;
0
,
2
5
;
3б
36.
Правильному применению методовможно научиться, только применяя их на
различных примерах
Цейтен
37. Рефлексия:
• Какую цель ставили перед собой науроке?
• Cмогли ли её достичь?
• Какой метод вам больше понравился?
• Оцените свою деятельность на уроке.
38. Итог урока:
1. Мне все понятно, у меня всеполучается!
2. У меня еще есть ошибки, но я
стараюсь!
3. Я ничего не понимаю,
у меня ничего не получается!
39. Домашнее задание:
№355(2,4,6), №356(1,3), №357(2),№358(4), №360(2)
40.
41.
Ресурсы:1. Алимов Ш.А., Алгебра и начала математического
анализа, Москва, Просвешение , 2017
2.https://nsportal.ru/shkola/algebra/library/2012/11/
30/prezentatsiya-svoystva-logarifmov
3.Мордкович А.Г. Алгебра и начала анализа. 10 – 11 кл.:
Учебн. для общеобразоват. учреждений. – 3-е изд. –
М.:Мнемозина, 2015.
4.Алгебра и начала анализа. 10 – 11 кл.: Задачник для
общеобразоват. учреждений/А.Г.Мордкович, 3-е изд.,
испр. – М.:Мнемозина, 2015.






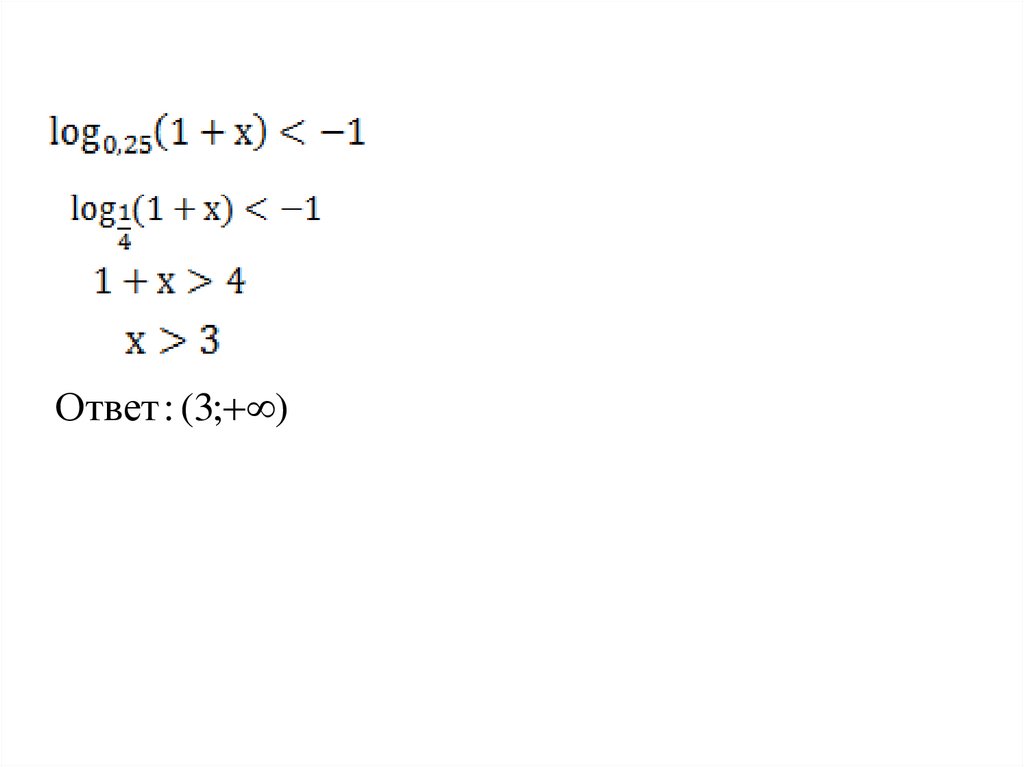
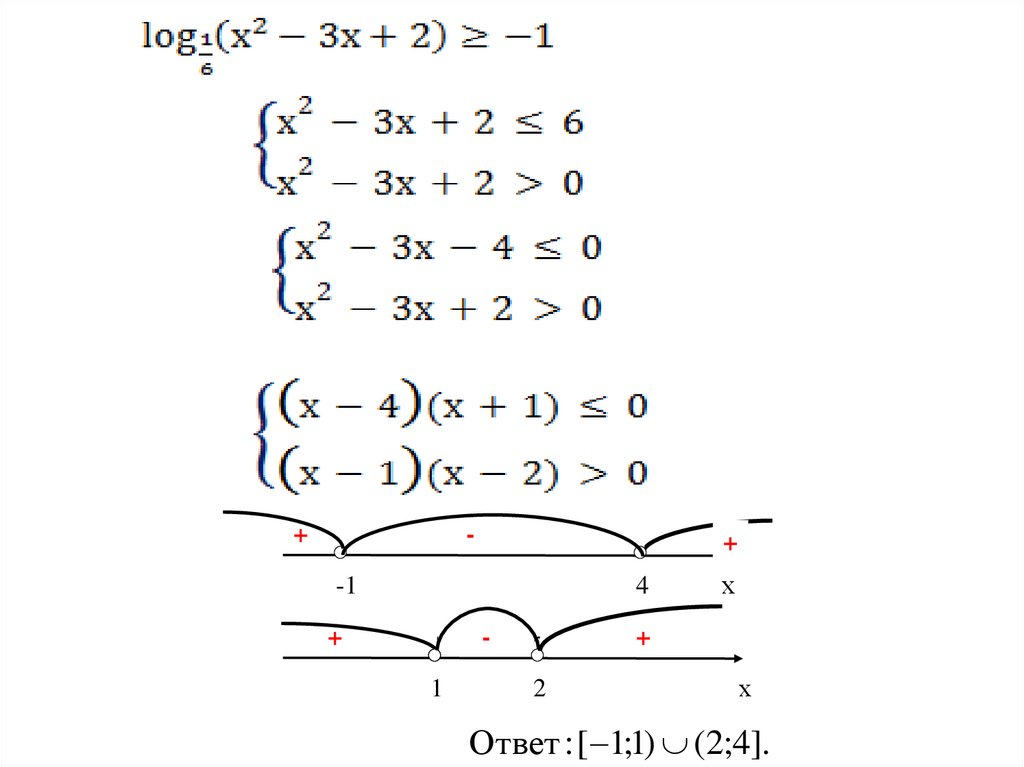





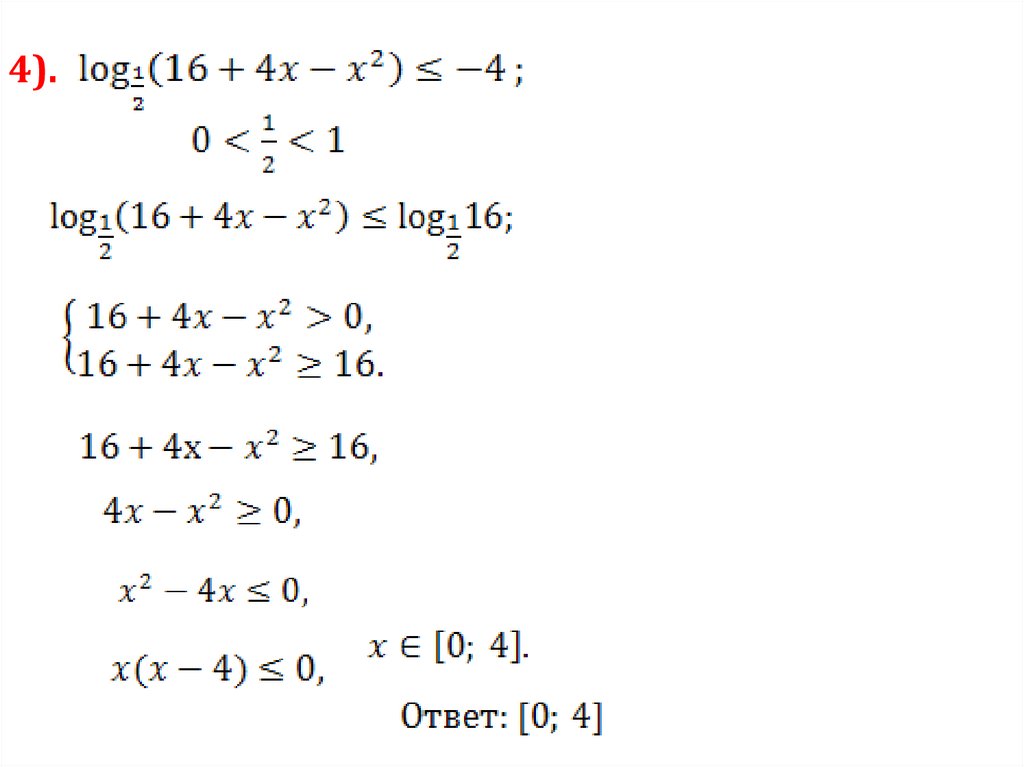
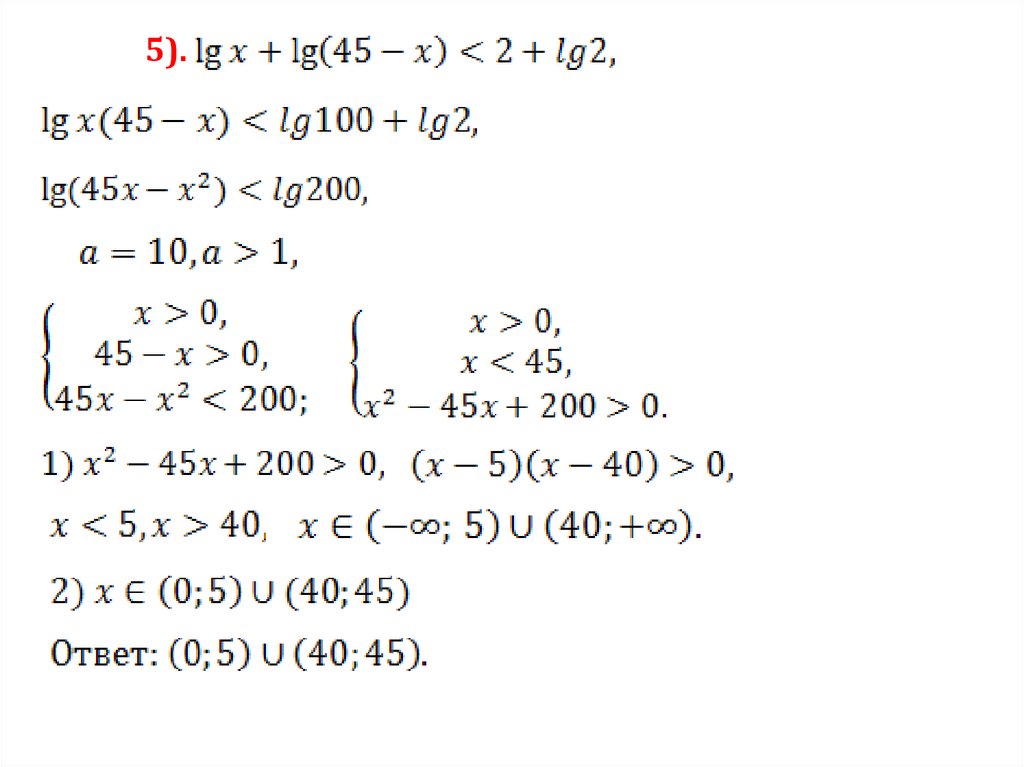
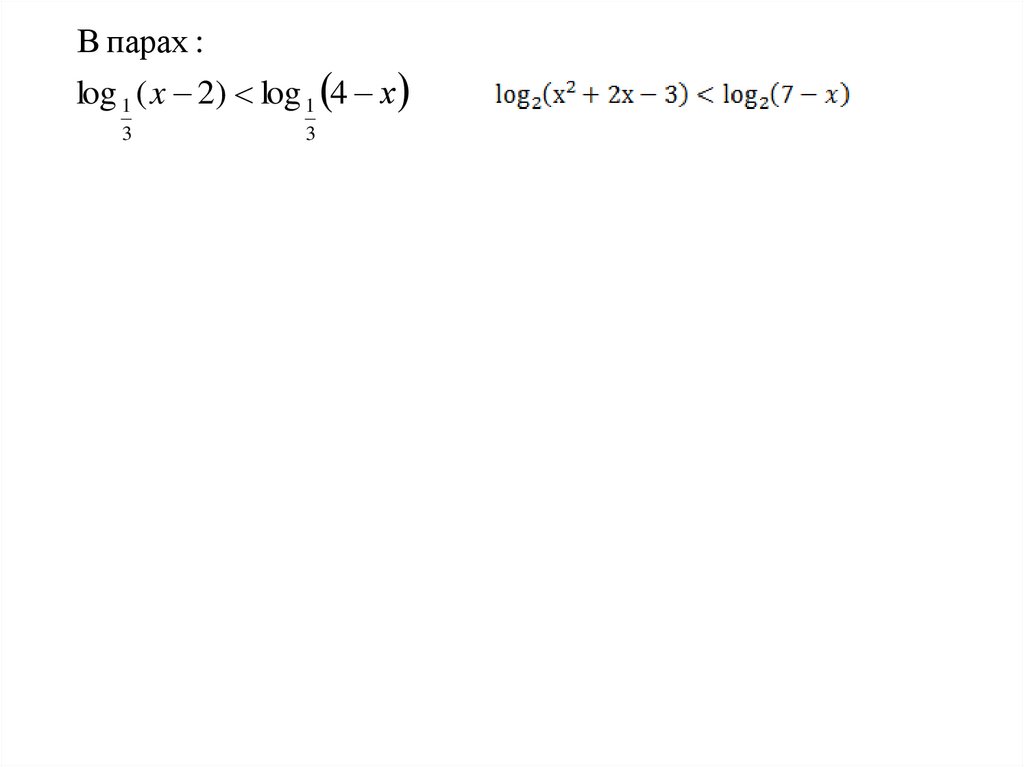
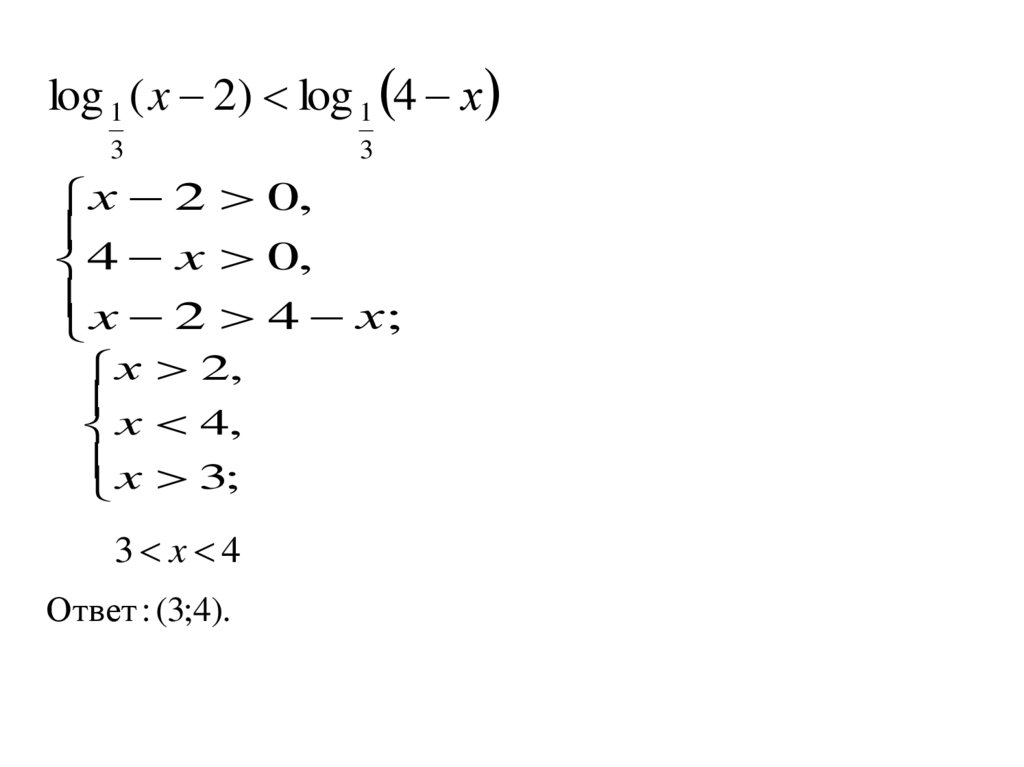


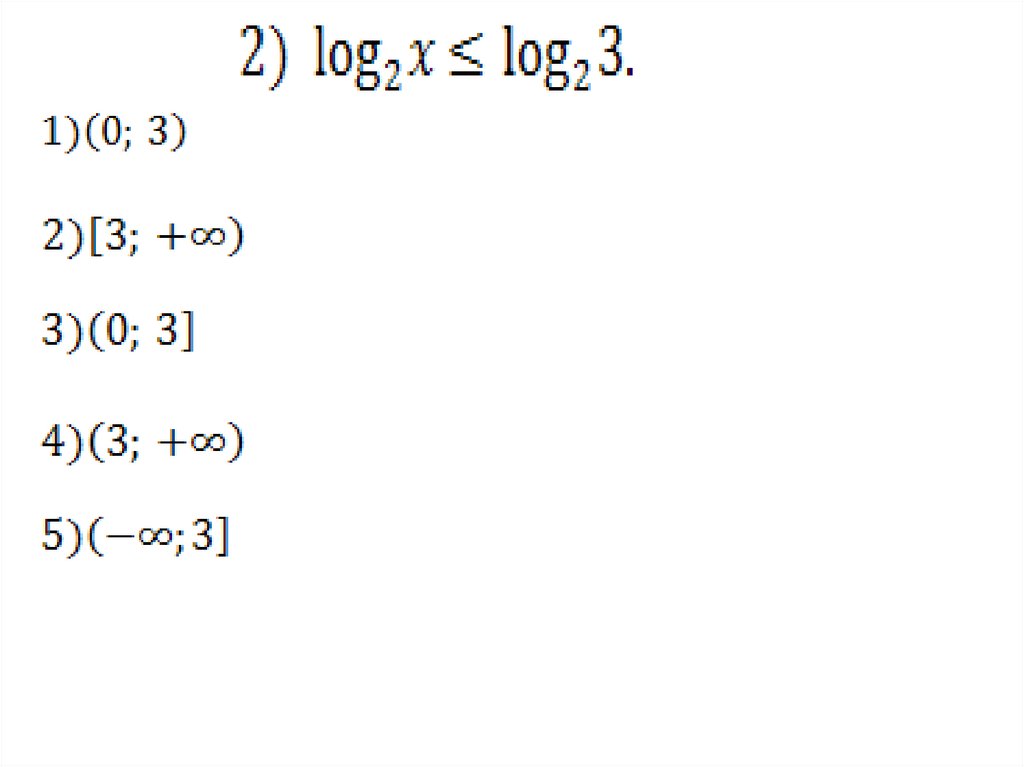




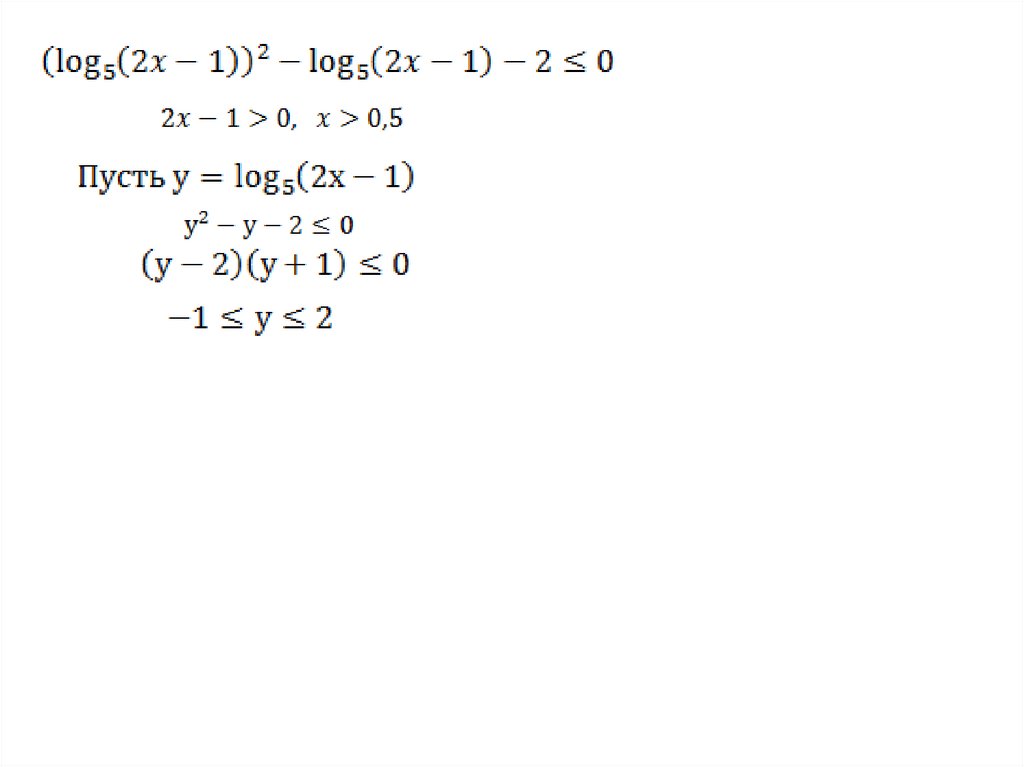
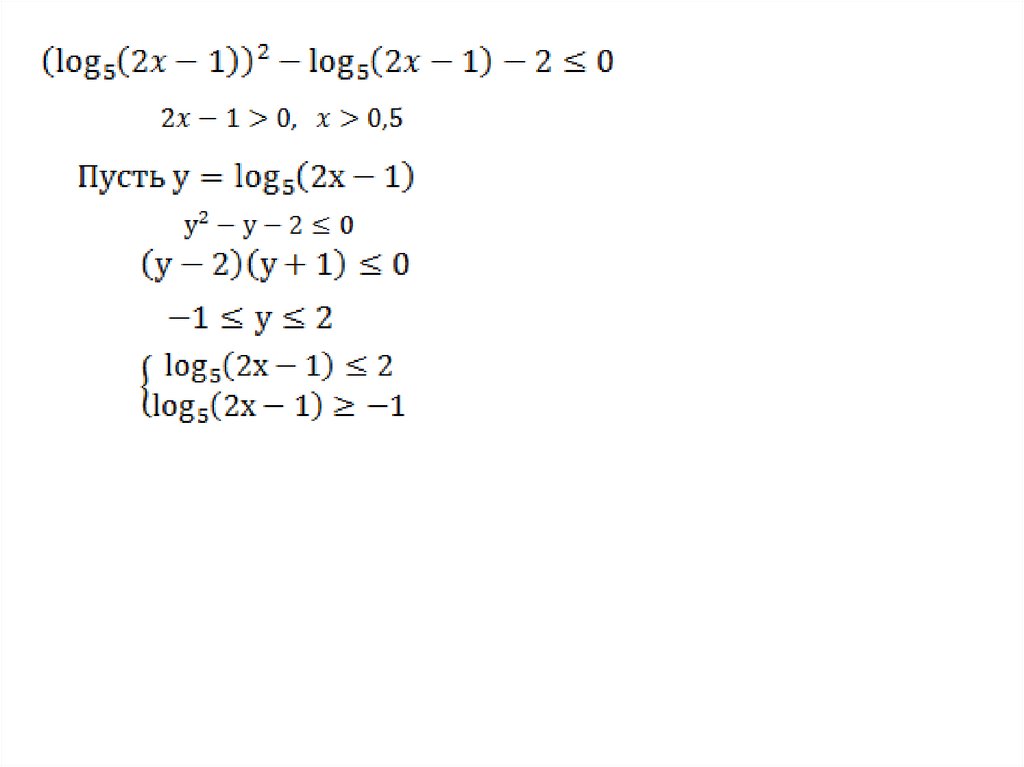
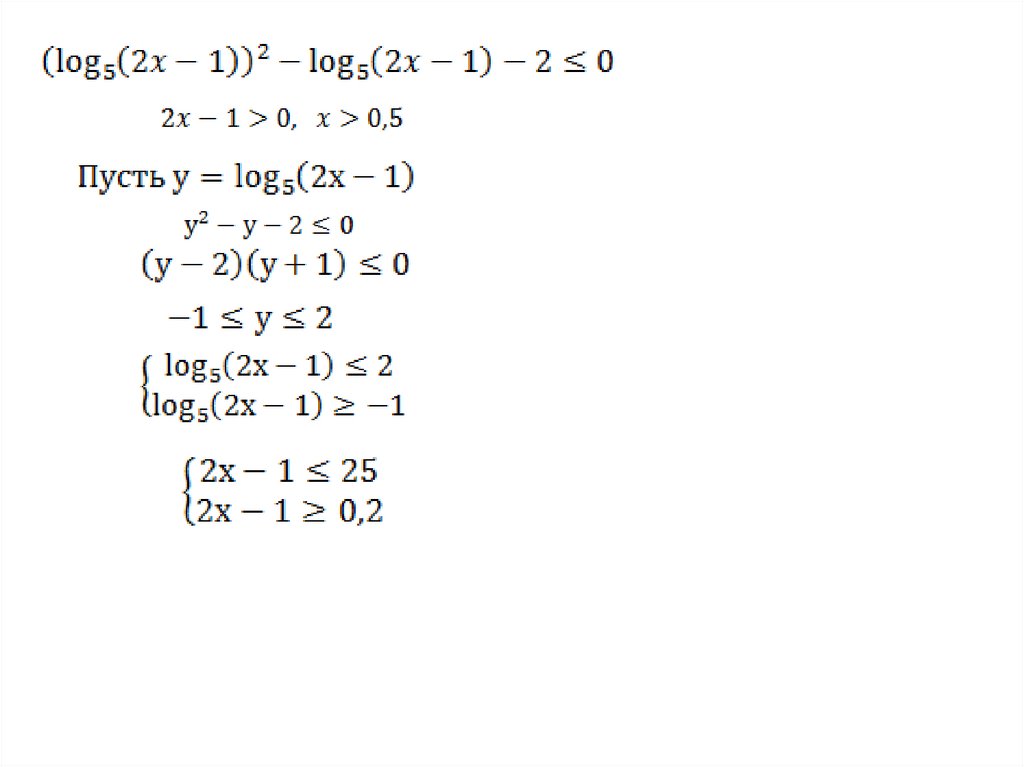
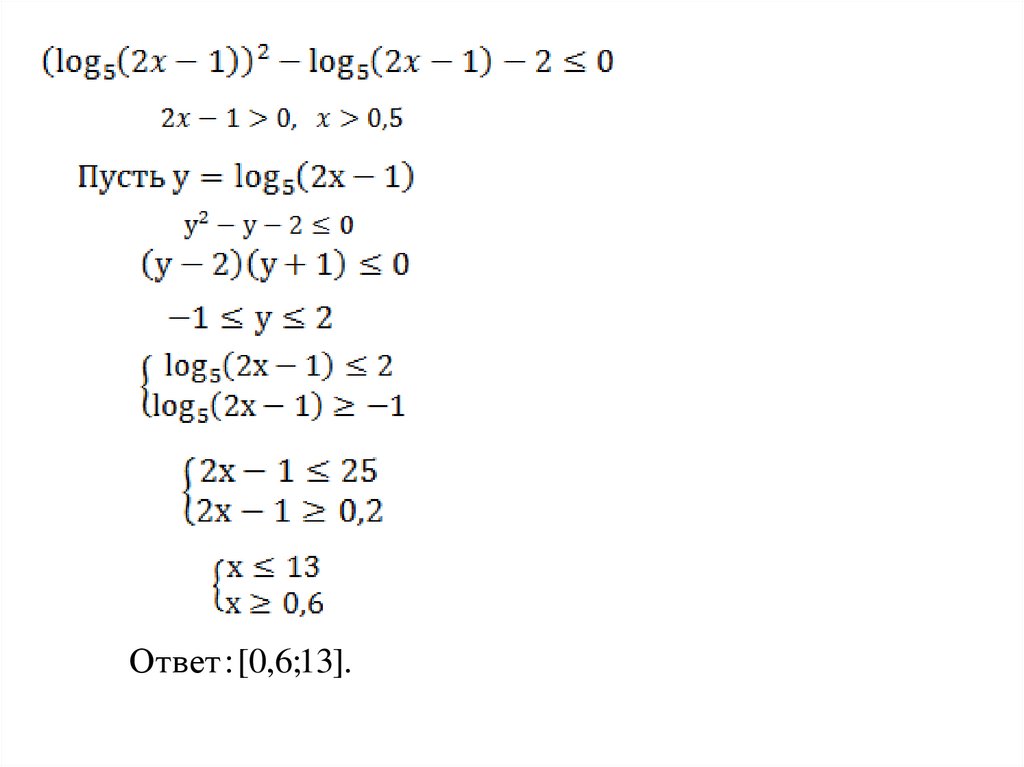









 mathematics
mathematics








