Similar presentations:
Логарифмические неравенства. (11 класс)
1. «Логарифмические неравенства»
11 класс2.
Повторение1.Вычислите:
а) log√39; б) log162; в) log2 32
2. Упростите:
а) log 3 8 + log 32;
б) в) 2log 3 4 – log 3 83.
3.Известно, что log 2 3 a.
Найдите: log 3 4
3.
Найдите область определения функций:а)
;
Повторение
б)
;
в)
;
г)
;
д)
.
4.
По определению логарифмаПростейшие логарифмические неравенства записывается
следующим образом: log a f ( x) b log a f ( x) b
Схема сравнения логарифмических неравенств.
logа x > b
0<a<1
0 < x < ab
logа x < b
a>1
0<a<1
a>1
x > ab
x > ab
0 < x < ab
5.
Метод потенцированияСуть метода в следующем: с помощью формул
неравенство привести к виду log a f ( x) log a g ( x)
Справедливы следующие утверждения:
f ( x) g ( x),
log a f ( x) log a g ( x) f ( x) 0, a 1
g ( x) 0;
f ( x) g ( x),
log a f ( x) log a g ( x) f ( x) 0, 0 a 1
g ( x) 0;
6.
Метод замены (подстановки)Ищем в неравенстве некоторое повторяющееся
выражение, которое обозначим новой переменной, тем
самым, упрощая вид неравенства. В некоторых
случаях, очевидно что удобно обозначить.
7.
Какой системе равносильно неравенство:log 2 x log 2 5
х 5,
х 5,
2.
1.
x 0;
0 x 1
х 5,
3.
x 0;
8.
Найдите ошибку.log8 (5х-10) < log8(14-х),
5x-10 < 14-x,
6x < 24,
x < 4.
Ответ: х (-∞; 4).
Ошибка: не учли область определения неравенства.
Верное решение:
log8 (5х-10)< log8(14-х)
2<x <4.
Ответ: х
(2;4).
9.
Решение логарифмических неравенствОтвет : (3; )
+
+
-1
+
4
1
1
-
2
х
+
2
Ответ : [ 1;1) (2;4].
х
10.
Решить неравенство :log 1 ( x 2) log 1 4 х
3
х 2 0,
4 x 0,
x 2 4 х;
х 2,
x 4,
x 3;
3 x 4
Ответ : (3;4).
3
+
-
+
-5
2
+
-3
х
+
1
Ответ : ( 5; 3) (1;2).
х
11.
Ответ : [0,6;13].12.
Решить самостоятельно1). log 1 х 4
3
2). log
1
36
(3x 3)
1
2
3). log ( x 2 4 x 3) 1
8
4). log 1 ( x 2 3x 4) log 1 (8 x)
4
4
5). log 1 ( x 4) log 3 (4 х) 1
3
6). lg x lg x 6 0
2
7).2 log x log 1 (5 x) 2
2
5
5
13.
Ответы :1
1
.(
0
;
)
1б
81
1б 2.( 1;1]
1б 3. ; 1 5;
2б 4. ; 6 2;
2б 5. 2;4
3б 6. 0;0,01 100;
1, 5
7
.
0
;
0
,
2
5
;
3б
14.
Реши самостоятельно.log x (2 x 1) log x (3x 5)
log x 2 (2 x 3) log x 2 (24 6 x)
15.
Реши самостоятельно.Решить неравенства:
log 2 x 3 x 1;
log x 1 (6 x 9) 0.
log 3 x
x 4
2,
2
x 3
2
21
x
3 x 12
3
2
x 6x
3
x 4










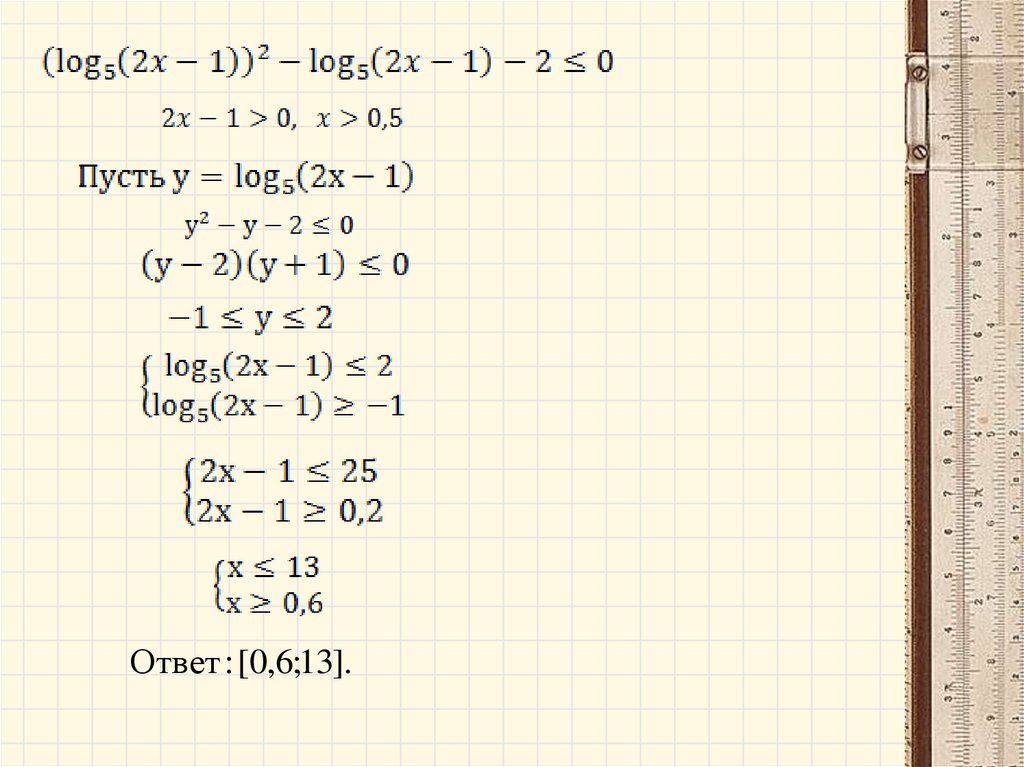





 mathematics
mathematics








