Similar presentations:
Векторная алгебра. Основные определения
1. ВЕКТОРНАЯ АЛГЕБРА
Основные определения2. Векторы
Определение. Вектором назовёмнаправленный отрезок, т.е.
отрезок прямой, ограниченный
двумя точками, одна из которых
называется начальной, а другая
конечной.
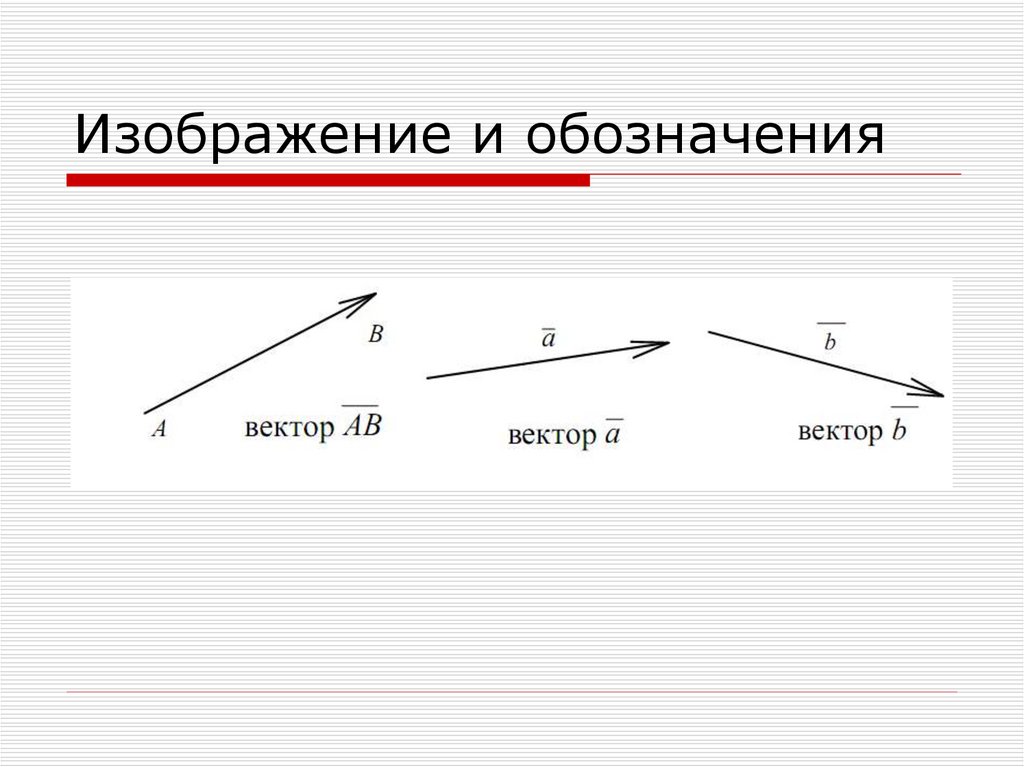
3. Изображение и обозначения
4.
5.
6. Компланарные векторы
Вектор, точка приложения которого может быть выбрана произвольно,называют свободным.
7. Линейные операции над векторами
К линейным операциям относятсяоперации умножения вектора на
число, сложения и вычитания
векторов.
8.
9.
10.
11.
12.
13. Свойства линейных операций над векторами
14.
15. Линейная зависимость векторов. Аффинный базис
16.
17.
18.
19. Базис на плоскости
20. Базис в трехмерном пространстве
21. Проекция вектора на ось
22. Теоремы о проекциях
23. Прямоугольный декартов базис
24.
25. Длина вектора
26. Длина вектора, заданного концами – расстояние между точками
27. Направляющие косинусы вектора
Направление вектора в пространстве определяется угламиα, β и γ между вектором и положительным
направлением соответствующих осей координат ОХ,
ОУ, ОZ; cos α, cos β и cos γ называются направляющими
косинусами вектора.
28.
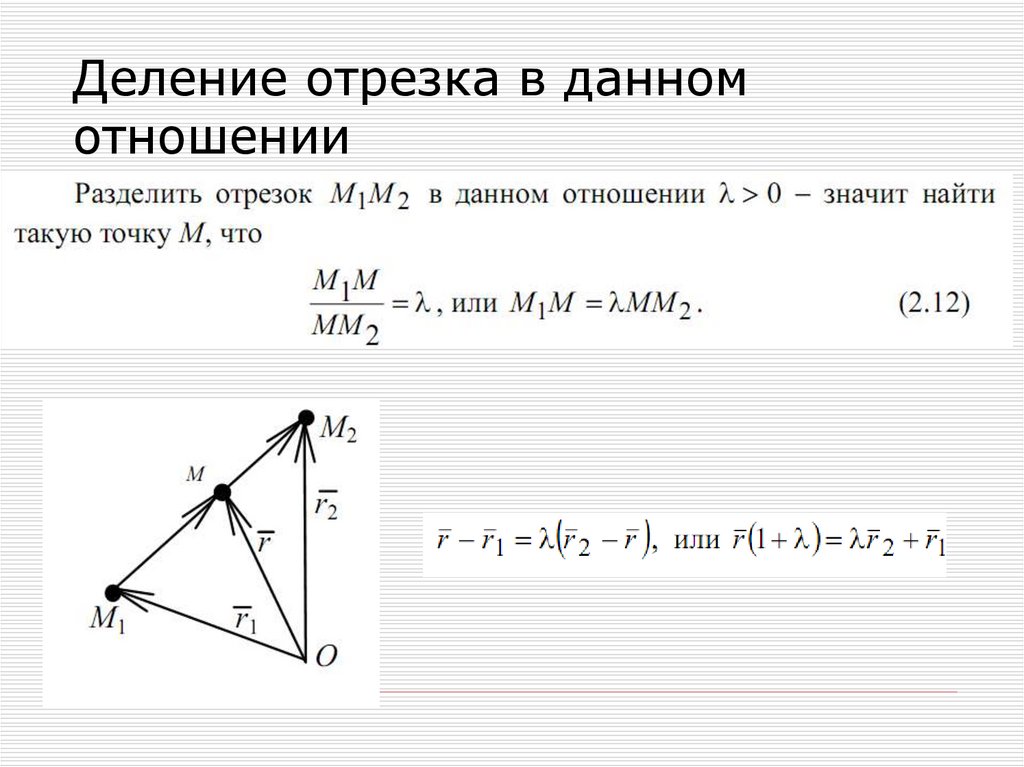
29. Деление отрезка в данном отношении
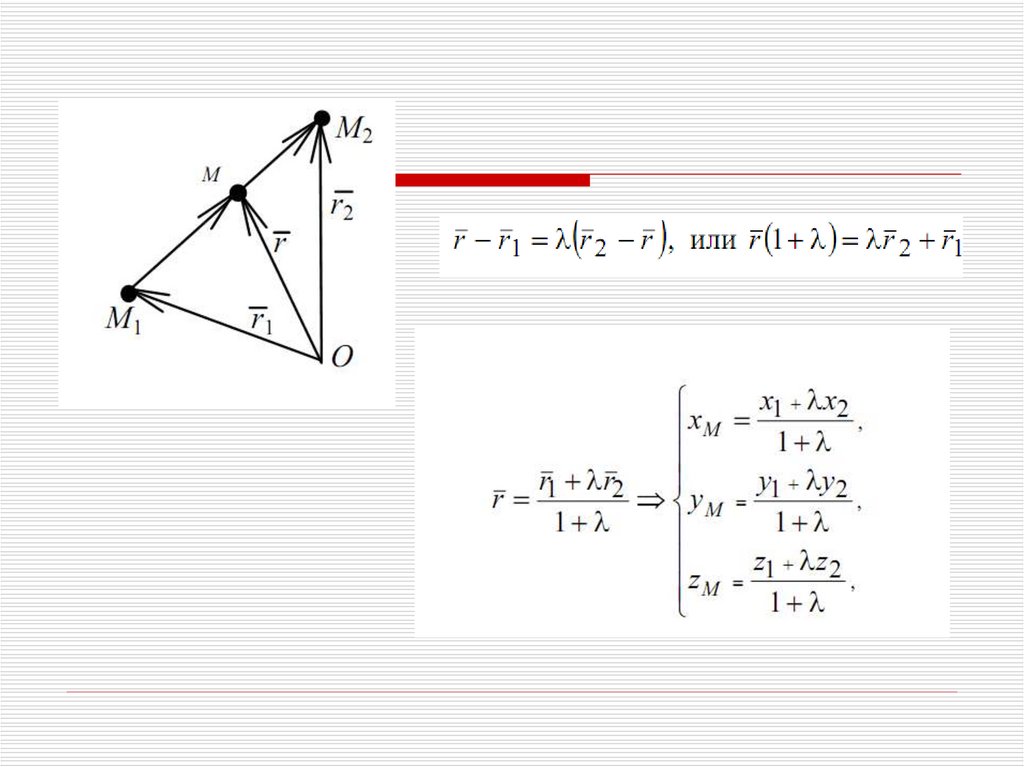
30.
31. Скалярное произведение
32. Свойства скалярного произведения
33.
34. Вычисление проекции вектора на вектор
35. Скалярное произведение в декартовой системе координат
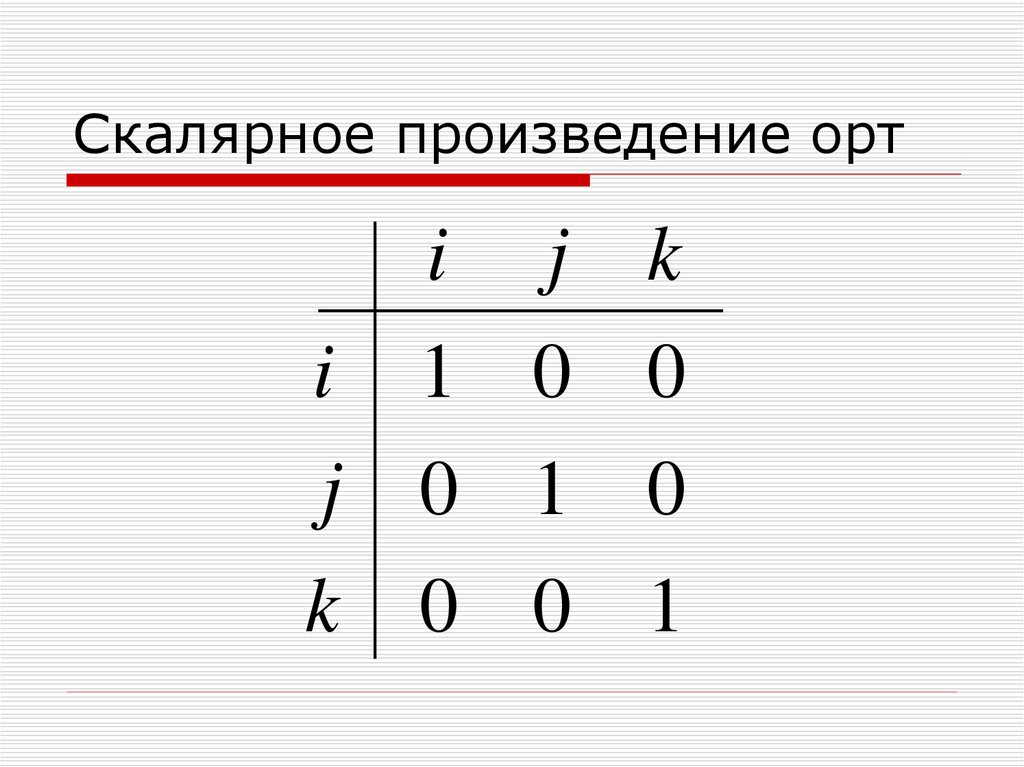
36. Скалярное произведение орт
ii
j k
1 0 0
j 0 1 0
k
0 0 1
37.
Скалярное произведение векторов равно суммепроизведений их одноименных проекций
38. Итоговые формулы
39. Векторное произведение
40.
Модуль векторного произведения41. Основные свойства векторного произведения
42.
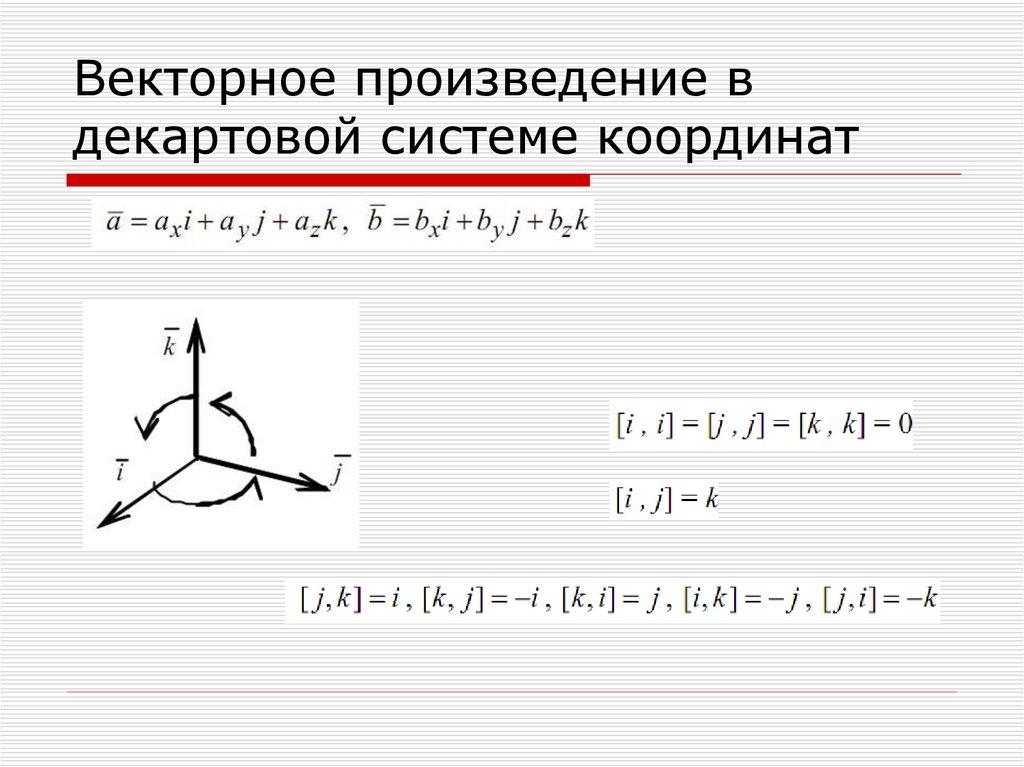
43. Векторное произведение в декартовой системе координат
44. Векторное произведение орт
ij
k
i
0
k
j
j
k
0
i
k
j
i
0
45.
46.
С помощью определениявекторного произведения
можно решать задачу о
вычислении площади
треугольника,
построенного на
векторах как на сторонах
(рис 2.26).
47.
48. Смешанное произведение трёх векторов
49. Смешанное произведение в декартовой системе координат
Вычислим предварительно векторное произведение50.
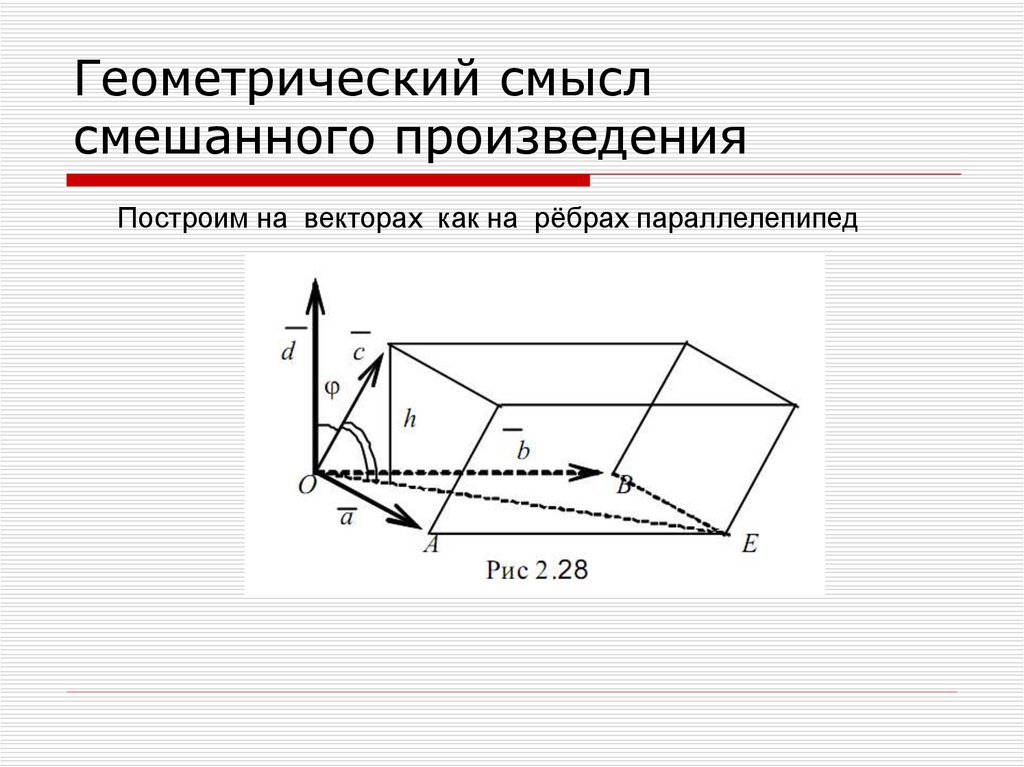
51. Геометрический смысл смешанного произведения
Построим на векторах как на рёбрах параллелепипед52.
53.
Вывод: модуль смешанного произведения трёхвекторов равен объёму параллелепипеда,
построенного на этих векторах как на рёбрах.
54. Свойства смешанного произведения
Все свойства смешанного произведениядоказываются с помощью свойств
определителя!







































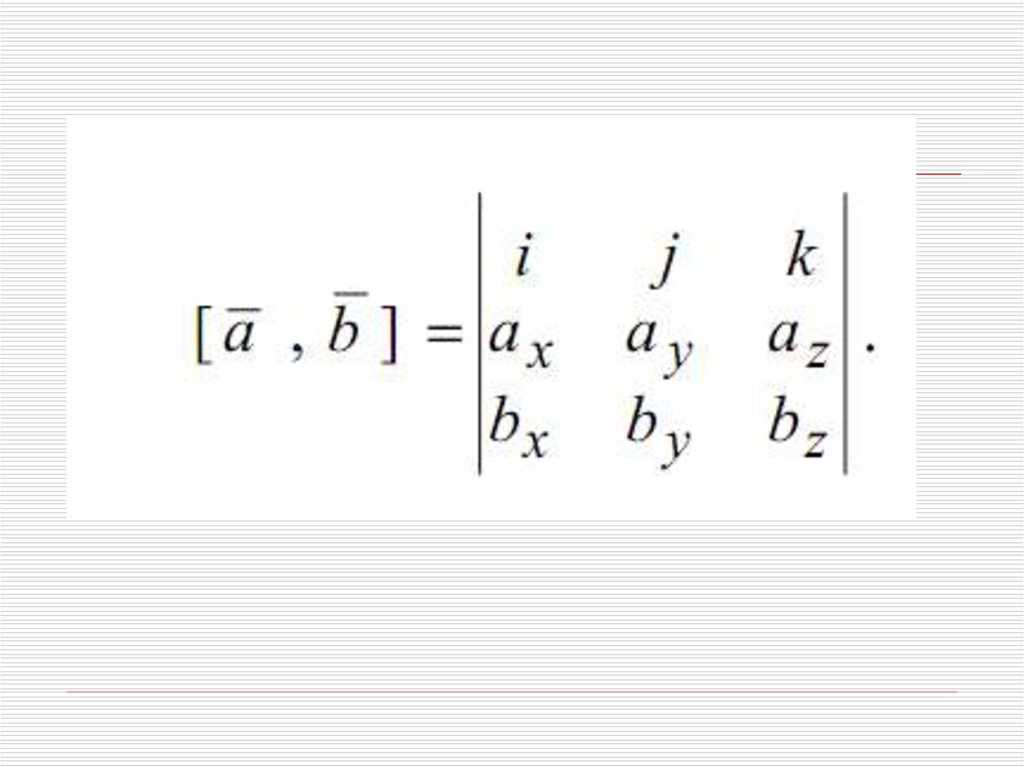









 mathematics
mathematics








