Similar presentations:
Теорема о площади треугольника
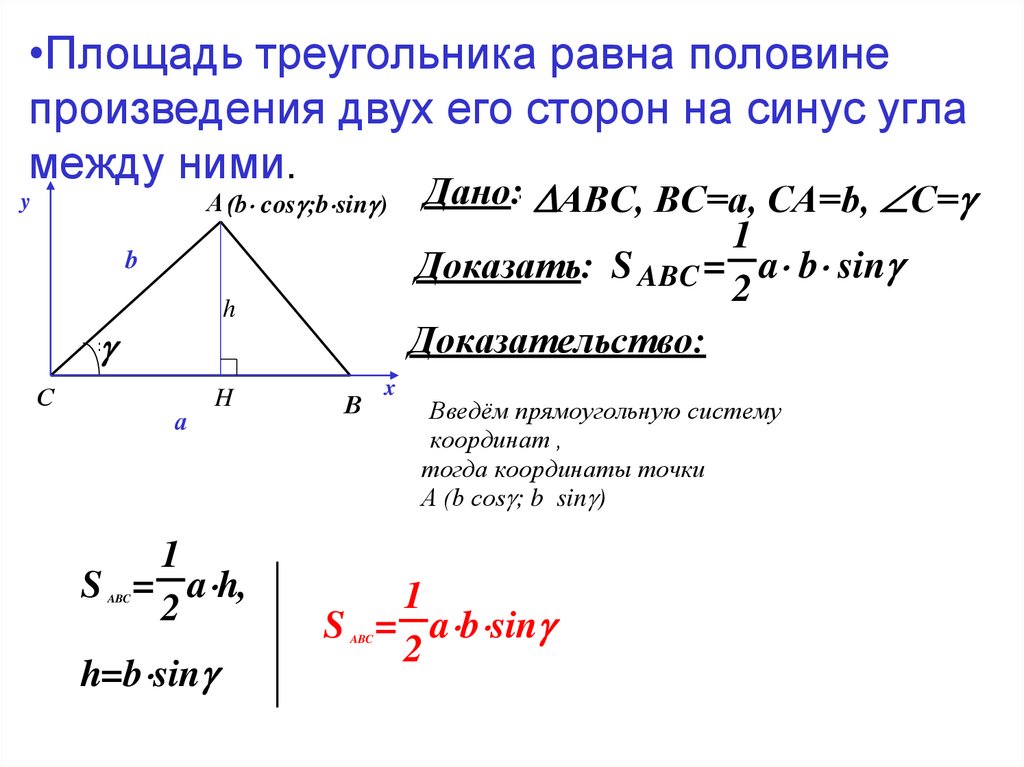
1. Теорема о площади треугольника
2.
•Площадь треугольника равна половинеу
у произведения двух его сторон на синус угла
Дано:
АВС,
ВС=а,
СА=b,
С=
у
Дано:
АВС,
ВС=а,
СА=b,
С=
между ними.
АА
А
1
уy
bb
bbb
Дано: АВС,
СА=b,
АВС, ВС=а,
ВС=а,
СА=b,
С=
С=
А
Дано:
АВС,
ВС=а,
СА=b,
С=
А(b cos ;b sin ) Дано:
1
Дано:
АВС,
ВС=а,
Доказать:
=b sin
a b sin
А
Доказать:
S ABC S= ABC
a 11
12
1
2
Дано:
АВС,
ВС=а,
СА=b,
С=
А(b
cos
;b
sin
)
S
=
a
b
sin
Доказать:
Доказать:
S
=
a
b
sin
Доказать: SABC
ABC = a b sin
ABCДоказать:
22
S ABC =
2
h
2
1
Доказательство:
b
А(b
cos
;b
sin
)
СС
С
Доказательство:
Доказать:
S ABC =С=a b sin
ВВ
В
Доказательство:
aa
a
b, СС=
Дано:
АВС,
ВС=а,
СА=b,
h
2
х
В
a
b
Доказательство:
x
H
С
х
1
В
a
В
Введёмпрямоугольную
прямоугольнуюсистему
систему
Введём
sinА(b
cos ;b sinа ) h Доказать:
С
S ABC
В=
a координат
координат
, , хa b sin
Доказательство:
2 точки
тогдакоординаты
координатыточки
тогда
С
х
В
a
cos ;;bb sin
sin ))
1АА(b(bcos
h
Доказательство:
S = a h, h=b sin
2
1
SВ = х a h, h=b sin 1
2
S = a b sin
2
1
a h, h=b
S = sina b sin
2
b
ABC
ABC
ABC
ABC
3. Следствие 1
• Площадь параллелограмма равнапроизведению двух его смежных
сторон на синус угла между ними
a
S =a b sin
a
пар
=b, С=
sin
b
b
• ( докажите самостоятельно)
Диагональ параллелограмма , делит его на два равновеликих
1 С= СА=b, С=
А
Дано:
АВС,
Дано:
ВС=а,
АВС,
треугольника
:СА=b,
SΔ= ВС=а,
a b sin
, Sпар= a b sin
2
1
1
Доказать: S ABC
Доказать:
= a b Ssin
= a b sin
ABC
2
2
оказательство:
Доказательство:
В
4. Следствие 2
у• Площадь параллелограмма равна
половине произведения диагоналей на
синус угла
между
ними
А
Дано:
АВС,
ВС=а,
СА=b,
С=
С=
ABCDпараллелограмм,
Дано:
АВС,
ВС=а,
СА=b,
А
С Дано: АВС, ВС=а, СА=b, С=
1
А
b
12 , С=
ву параллелограмма
1AOB=α
BD=d
Дано: АВС,
ВС=а,
СА=b,
1 , AC=d
S=
d
d
sin
1
2
А
d
d
Доказать:
S
=
a
b
sin
1 1 2 2 b
Доказать:
S
=
a
b
sin
ABC
1
1
O
ABC
1
sin ,
2
Доказать:
S
=
a
b
sin
2 ad b sin
2 2 2
ABC S S= =
Доказать:
sin
d
2
ABC
1
2
По
свойству
параллелограмма
1d 1 d 2 b 180°-α
ПоПо
свойству
свойству
параллелограмма
параллелограмма
d
d
d
d
1
1
2
1 свойству
2
2
2
По
параллелограмма
sin
С) =a
Доказательство:
d 1 Сd
sin(180
sin
=
sin
,
Доказательство:
В
d 1d 1d 2d 2По
1 1d 1d dпараллелограмма
2d
2 2 12 1В
8 свойству
22 2С 2
1
2sin ,
Доказательство:
Sa1S=S
=S
=3D= В S 1 Доказательство:
sin
sin
,
,
=S
=
d
d 2sin ,
1
3
3
1
1
А По свойству
параллелограмма
2 2 2 2 2 S21 =S 3 =
2 2 2
ПоПосвойству
параллелограмма
По
свойству
свойству
параллелограмма
параллелограмма
В
b
a
S 1 =S 3 =2 2 2
sin ,
2
2
2
d
d
d
d
d
d
d
d
d 1 dd
d1 2d12d1х2 1 2 2
С
1 1d 1d 1d12d12 1 1d 2d 2
11d 1ddd 1d112 d d2d22
d 1 a1d 2 11 1d21
d1dВ
d
11 d12
1
2
S
=S
==S
=S
=2 ==S
sin
, sin
Ssin
S =S
=
=
sin
sin(180
sin(180
)
=
)
=
sin
sin
=
=
sin
sin
,
,
параллелограмма
AOB
COD
d
d
d
d
d
=
sin
,
=S
=
sin
,
,
S
=S
=
sin(180
)
=
sin
=
1 1=S
= 4S Sсвойству
=4S3 1S
2
4
4
парПо
1
1
1
2
1
2
1
3
1S
1
3
3
2
4
S 2 =S 42= 2 2
2 2sin(180
= 8
2sin(180
2 2 - -) =) 2=2 82 28 2 2 sinsin
82 2 2 2222 2222 2 22 2 2 2
2
2
2
2
S
=S
=
= 8
d
d
По свойству
параллелограмма
2
4
1 d1 d 2
d
d
d
d
2
2
2
2
2
2
8
1
1
d
d
d
d
d
d
d
d
d
d
d
d
d
d
d
d
1
2
1
2
1
2
1 1 11 1 12 2 2
2 ,2
1 1 21 2 2
S 1 =S 3 = 1 1d 11 11d12sin12
==S
sin(180
)=
)sin
= sin
=
sin
SSBOC
=SS4AOD
S=S
=4 т.к.
sin(180
sin
sin(180
sin(180
-). 2=) = - 2 -)=
sin
sin
=sin ,sinsin sin
=42
=2
-
, , ,
2 =S
т.к.
sin(180
-
--, sin(180
)=
22
2 4=S
2S
т.к.
=2. sin
S 1 =S
sin(180
2-.) sin(180
8 = =
т.к.
)=
sin
. sin
2
2
2
2
2
2
2
2
2
2
8
8
2
2
8
32= 2 2 222
т.к.
ddd112d 2d 2- )=d sin
1 d21 2d 2 2
1d 1sin(180
1d d
1d d
2.dd21d d 2
dd,11 dd22
1 1sin
2 sin
2 sin
S 2 =S 4 = 1 Значит
Значит
sin(180
)
=
sin
=
,
S
,
S
=
4
=
S
4
S
=4
=4
sin
sin
=
=
пар
пар
d
d
d
d
d
d
1 Значит
1 21, S2
12sin2 .
2 S
2sin =
2
Значит
424·S
2 2 1d 18 2dsin
,пар8S1 =
4 1SΔ=4
=4
= d 1 d sin
пар =
2
2
т.к.
sin(180
)=
8
1
т.к.
т.к.
sin(180
sin(180
)=
)=
sin
sin
.
.
т.к.
sin(180
)=
sin
.
S 2 =S 4 =
sin(180 - ) =
, S пар =sin
= 8 8
sin
Значит
4 S =4
sin , = 22
sin
2 2 2 d 1 d 2d 1d 1dd2d1 2d22d 1 2d d2 1d21d 21d 2d 21
88
2
Значит
, Значит
S пар
SS,пар
sin sinsin sin
т.к.
sin(180
-=
, )=
sin
Значит
=
sin
=
=
==
Значит
S4, пар
=
4 4=
S . 1S4=4
sinsin
sin
1S=4
пар
1 S8=4
1 =4
2
8
8
2
2
8
2
т.к. sin(180 - )= sin d. 1 d 2
d1 d2
0 - )= sin .
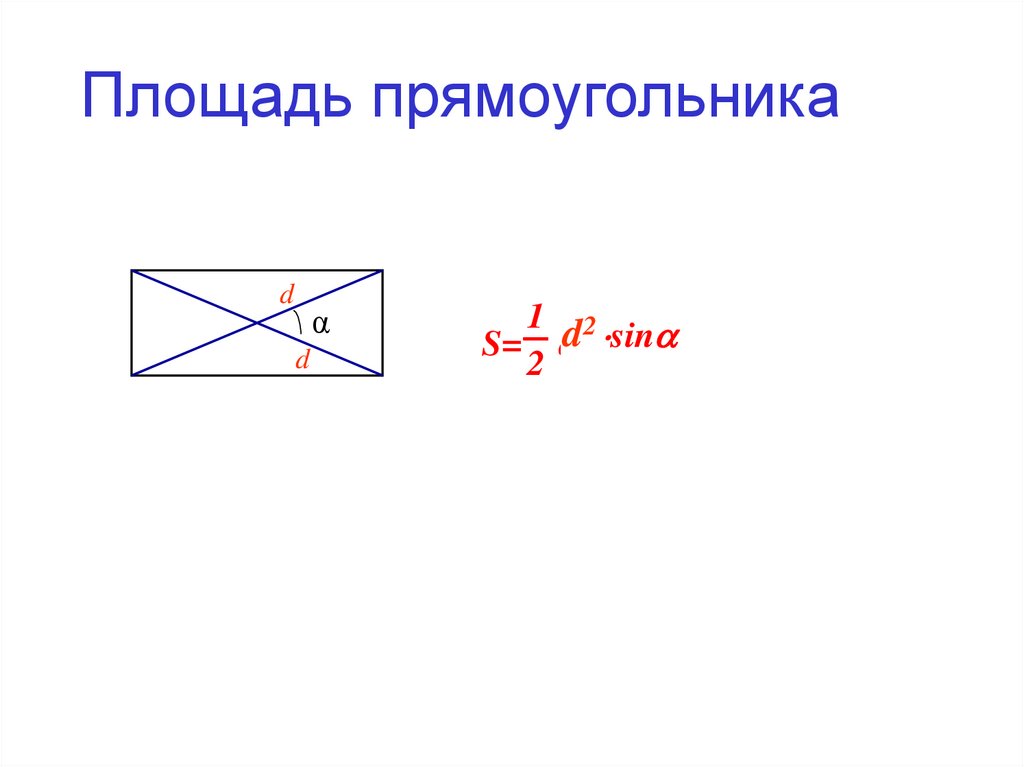
5. Площадь прямоугольника
dα
d
1 1 2
S= S=
d 1 dd12 sin
d 2
sin
2 2
6.
Площадь произвольного четырёхугольникаА
А
b
А bd
Bb
180°-α
b
С
С
С
Oa
a
СA
a
1
α
a
ABCD4-угольник,
Дано:
АВС,
ВС=а,
СА=b,
С=
Дано:
АВС,
ВС=а,
СА=b,
С=
Дано:
BD=d
АВС,
ВС=а,
СА=b,
С=
А
C Дано:
1
АВС,
ВС=а,
СА=b,
С=
.
AC=d
,
СOD=α
1
1
2
Доказать:
S ABC
a1 ba sin
sin
1S 1= =
Доказать:
b
ABC
Доказать:
S
=
a
b
sin
2 da2 bsin
ABC S
Доказать:
sin
S=
2ABCd=1 2
2 2
Доказательство:
В
Доказательство:
В
d2 В
Доказательство:
Доказательство:
В
х
SABCD=SABO+SBOC+SCOD+SAOD
D
S AOB
S COB
1
AO BO sin
2
ABCD
1
1
CO BO sin( 180 ) CO BO sin
2
2
1
CO DO sin
2
1
1
DO AO sin( 180 ) DO AO sin
2
2
S COD
S AOD
SS AOB =
1
1
AO BO sin CO BO sin +
2
2
1
1
CO DO sin DO AO sin =
2
2
1
1
BO sin AO OC DO sin AO OC =
2
2
AC
AC
1
АC sin BO OD 1 АC BD sin
2
2
BD
1
S= d 1 d 2 sin
2
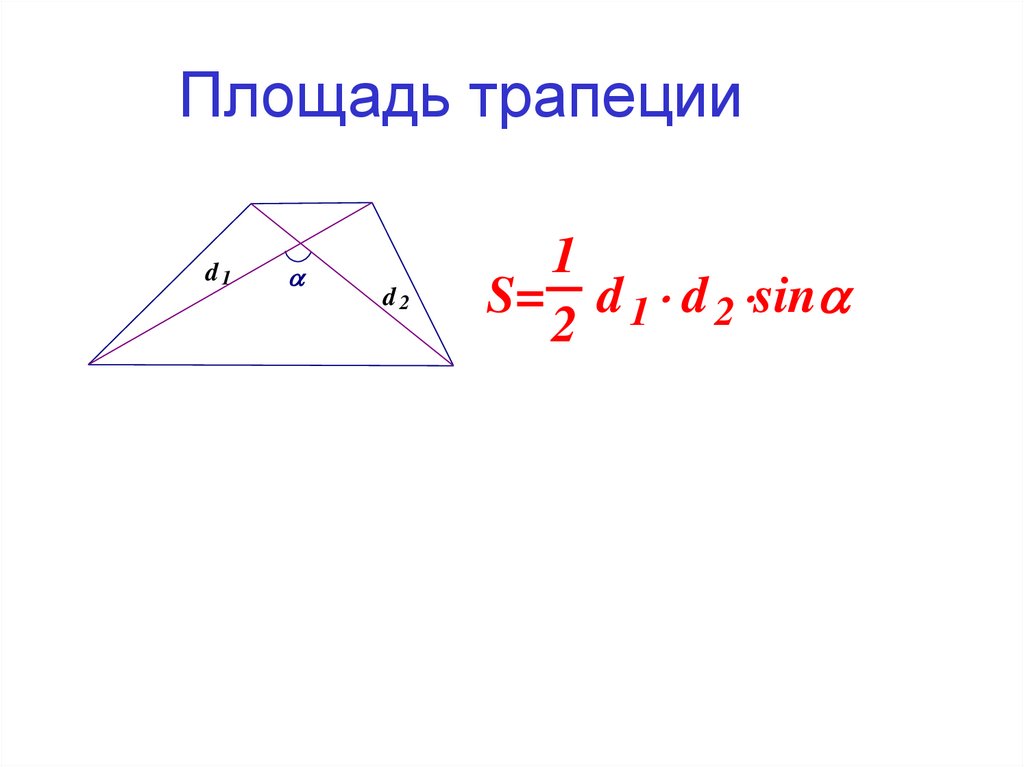
7. Площадь трапеции
d1d2
1
S= d 1 d 2 sin
2
8.
Задания по готовымчертежам
9.
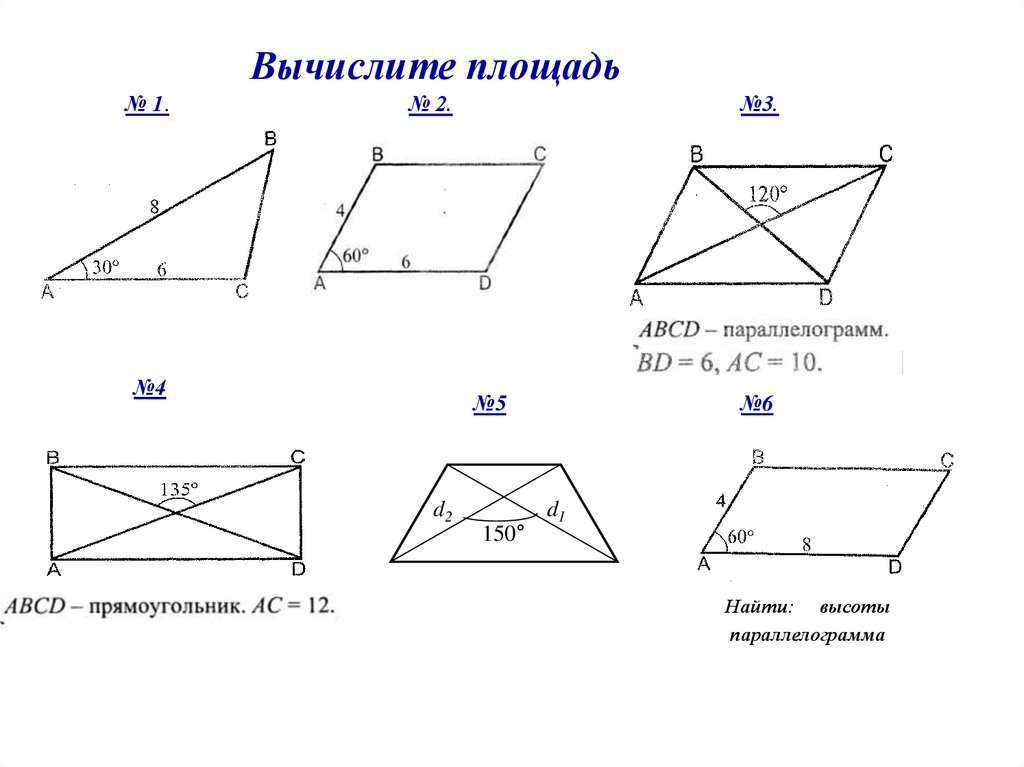
Вычислите площадь№ 1.
№ 2.
№4
№3.
№5
d2
150°
№6
dd11
Найти: высоты
параллелограмма
10. Теорема синусов
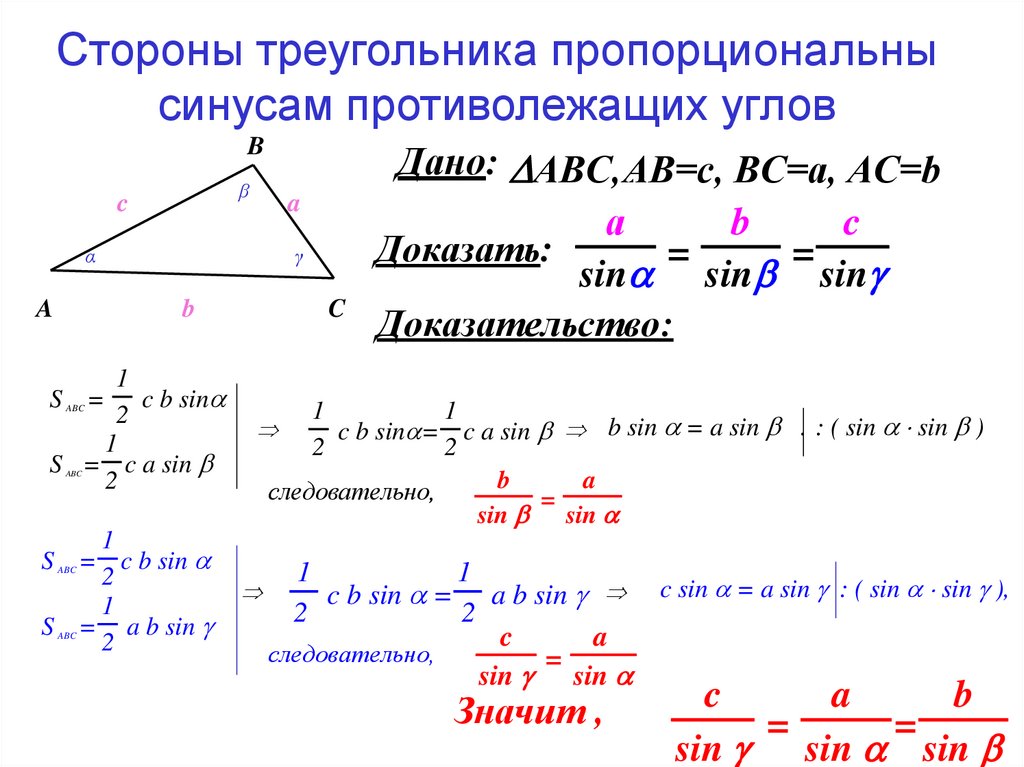
11. Стороны треугольника пропорциональны синусам противолежащих углов
Дано:АВС,
ВС=а,
СА=b,
С=АС=b
Дано:
АВС,
АВ=с,
ВС=а,
B
Дано:
АВС,
АВ=с,
ВС=а,
АС=b
Дано:
АВС,
АВ=с,
ВС=а,
Дано:
АВС,
ВС=а,
СА=b,
АС=b
С=
Дано:
АВС,
АВ=с,
ВС=а,
АС=b
β
1
a
аа а= a1 bbb bsin ccc c
aaaДоказать: S а
c
ABC =
a
Док-ть:
=
2
Док-ть:
=
=
Док-ть:
=
=
Доказать:
S
=
a
b
sin
sin
γ
Док-ть:
=
=sin
ABC
sin
sin
sin
sin
sin
sin
sin
b
C
sin 2 sin sin
bb b
CC C
C
Доказательство:
В
Доказательство:
Доказательство
Доказательство
Доказательство
Доказательство
А
c
A
С
А
α
b
A
A
A
A
b
a
С
ccc
b
B B
BB
1a
х
S = c b sin В
1
1
2
sin ==a asin
sin : (: sin
( sin sin
sin ) )
c b sin = c a sin b bsin
1
2
2
S = c a sin
b
a
2
следовательно,
=
sin sin
1
S = c b sin
1
1
2
c b sin = a b sin c sin = a sin : ( sin sin ),
1
2
2
S = a b sin
c
a
2
следовательно,
ABC
ABC
ABC
ABC
sin
=
sin
Значит ,
c
a
b
=
=
sin sin sin
12. Следствие 1
Отношение стороны треугольника к синусупротиволежащего угла равно двум радиусам
Дано:О(О;R),
BC=a,
A=
(диаметру)
описанной
окружности.
AА
А
Дано:
АВС,
ВС=а,
СА=b,
С=
A= α С=
B
А
Дано:
АВС,
ВС=а,
СА=b,
С=
Дано:О(О;R),
BC=a,
A=
A
Дано:
АВС,
ВС=а,
СА=b,
Дано:О(О;R),
BC=a,
Дано:О(О;R),
BC=a,
A=
A
A
Дано:
АВС,
АВ=с,
ВС=а,
АС=b
ω a
1b1 a c 1
a
а
a
А
Доказать:
SSABC
== =2R
aa S b=b =2R
sin
a b sin
Док-ть:
Доказать:
sin
Доказать:
=
ABC
Док-ть:
=2R
Док-ть:
Док-ть:
=
Док-ть:sinsin
=2R
22sin
ABC
O
О
sin
sin
sin 2
O
O
sin
O
b
C
a
Доказательство:
aBа a B Сa a ВB a Доказательство:
В
C
C
Доказательство:
С C C Доказательство 1 случай
b
b
A
BС
В
С
b a
А
1
αc
х
В
ВА
1)Проведём диаметр ВА
11
a
2)
Рассмотрим остроугольный треугольник
ВСА 1 : С=90 ( по свойству вписанного угла , опирающегося на диаметр)
3)3) А=
углов, опирающихся
опирающихся на
наодну
однудугу),
дугу),
А= АА== ((по
посвойству
свойству вписанных
вписанных углов,
значит,
значит,sin
sin A=
A=sin
sin
AA11 =sin
BCBC
aa
aa
4) 4) ВСА
ВСА
С=90
, sin
, sin
A
1A=1 = , т.е.sin
, т.е.sin
= = , отсюда
, отсюда2R=
2R=
1 :1 :С=90
BABA
2R
2R
sinsin
1 1
1 1
13.
2 случайΔАВС- тупоугольный
А
α
С
а
В
.
О
180°-α
А1
(докажите самостоятельно)
14. Следствие 2
• Площадь треугольника можно вычислитьa b c
по формуле S=
• a, b, c –
4R
стороны треугольника,
R – радиус окружности ,описанной около
треугольника .
( докажите самостоятельно, используя теорему о площади
Дано:О(О;R), BC=a,
Дано:О(О;R),
A=
BC=a,
A=
A
треугольника
и
следствие
из
теоремы
синусов
)
Дано:О(О;R),
BC=a,
A=
A СА=b,
ВС,
АВС,
ВС=а,
ВС=а,
СА=b,
С=
С=
Дано:О(О;R),
BC=a,
A= A
Дано:О(О;R),
BC=a,
A
a A
A
=2R
sin
O
ать:
: S ABC
S ABC
= сa= ba sin
b sin
Док-ть:
2 2
1 1
Док-ть:
O
B Ca
тельство:
ьство:
B
aO
a OB
CB
Значит,
B
a
a
Дано:О(О;R),
BC=a, A=
a Док-ть:
a =2R
a
=2R
sin
Док-ть:
a =2R =2R
Док-ть:
sin
sin
O Док-ть:sin =2R
sin
aCC a b c
C
S=C
4R
15.
Теорема косинусов16.
• Квадрат стороны треугольника равен суммеквадратов двух других сторон минус удвоенное
произведение этих сторон на косинус угла
y у
между ними. B
Дано: АВС,
АВС, ВС=а,
АВ= с,ВС=а,
АС=b,АС=b
Дано:
АВ=с,
СА=b,
С=
у
С
С(bcos
)
Дано:
АВС,
АВ=
с, АС=b,
c А ;bsin
A=
bСА=b,
а
c С=
Дано:
CB=a,
АВС,
ВС=а,
kj
b b
b
A
α
АС
А (0;0)
аА
a
c
1
CB=a,
A=
Док-ть:
=2=1 a2 =b sin
Доказать:
S
ABC
2
sin=b
sin
2-2bc
sin cos
2
Док-ть:
а
+c
C Доказать:
2
2
a b -2bc
sin cos
Док-ть:SаABC
=b= +c
2
Доказательство
х
Доказательство:
В(c;0Доказательство:
)
В
b
x
c
b
a
a
В(с;0)
С
х
В
a
Введём прямоугльную систему координат
По формуле расстояния между двумя точками получаем:
BC2= a2 = (b cosα –c)2 +b2sin2α = b2 cos2α - 2bc cosα +c2 +b2sin2α =
2
2
2
2
2
2
= b (cos α + sin α)+c - 2bc cosα = b +c - 2bc cosα
1
17. Докажите самостоятельно , используя теорему косинусов , следующее утверждение:
• Сумма квадратов диагоналейпараллелограмма равна сумме
квадратов его сторон.
d1
а
d2
b
d
1
2 +d 2 =
2
2
2
2a +2b
18. Задания по готовым чертежам
19.
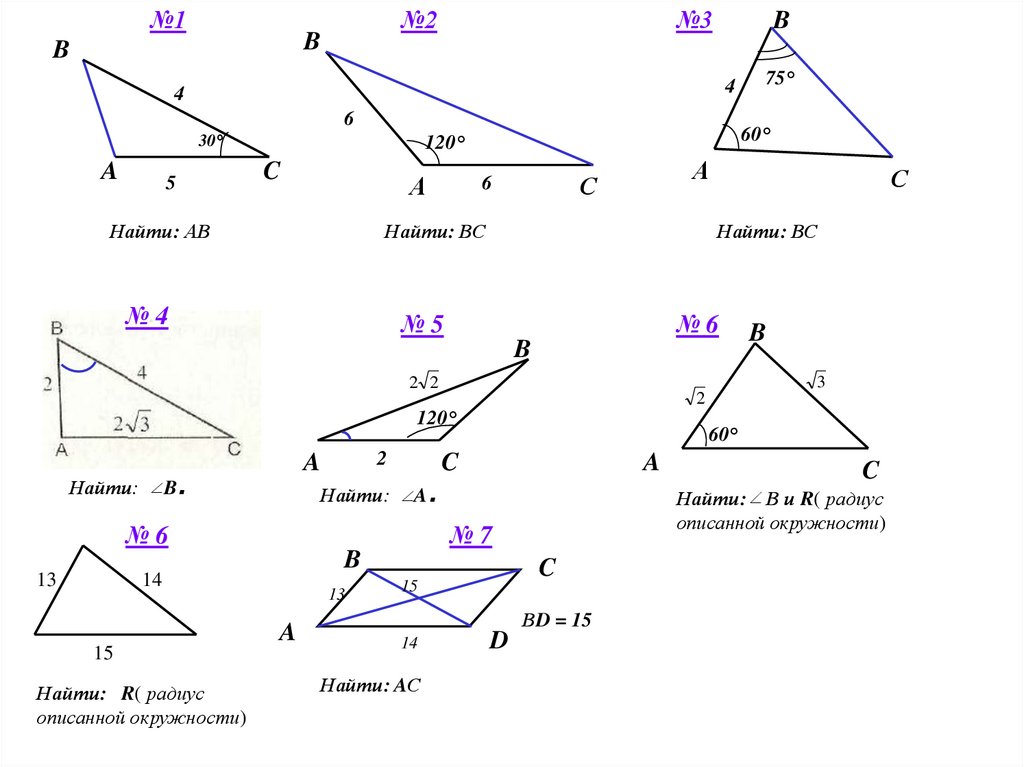
№1№2
B
B
№3
B
4
4
6
30°
A
60°
120°
C
5
А
Найти: АВ
А
С
6
Найти: ВС
№4
75°
С
Найти: ВС
№5
№6
B
B
3
2 2
2
120°
Найти:
2
A
.
B
Найти:
.
Найти: R( радиус
описанной окружности)
A
B
13
A
C
15
14
Найти: AС
D
C
Найти: В и R( радиус
описанной окружности)
№7
14
15
C
A
№6
13
60°
ВD = 15
20. Задания по готовым чертежам
21.
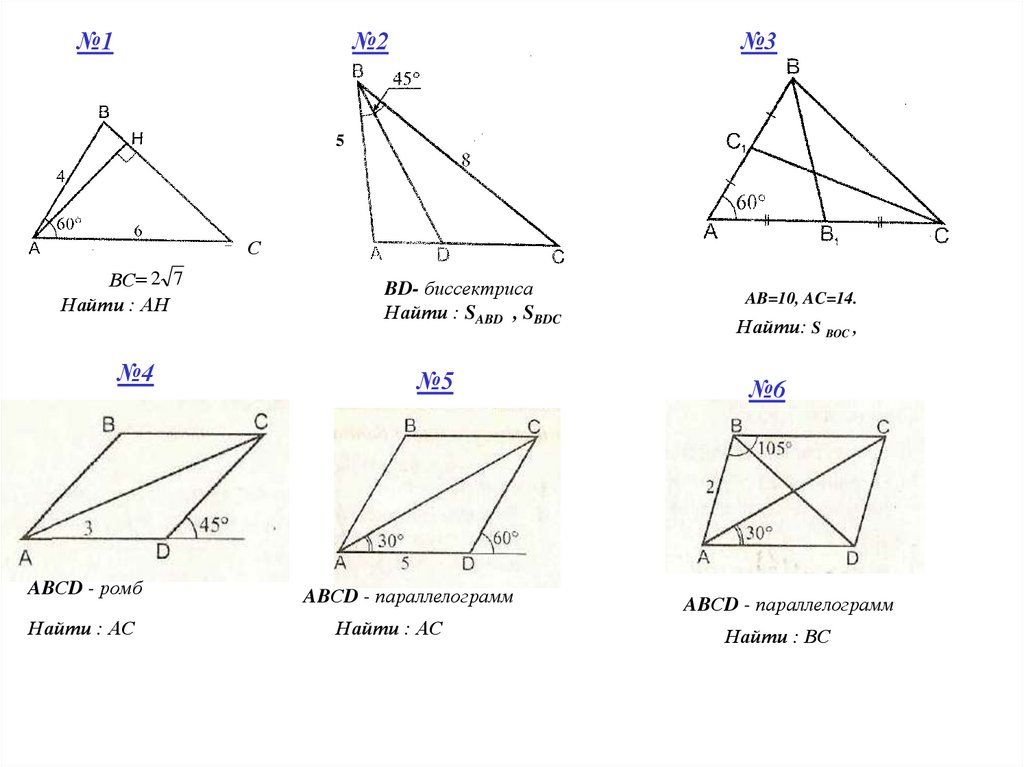
№1№2
№3
5
С
ВС= 2 7
Найти : АН
№4
ABСD - ромб
Найти : АС
BD- биссектриса
Найти : SABD , SBDC
№5
ABСD - параллелограмм
Найти : АС
AB=10, AC=14.
Найти: S BOC ,
№6
ABСD - параллелограмм
Найти : ВС














 mathematics
mathematics








