Модуль числа. Уравнения и неравенства, содержащие модуль

1.

Модуль числа. Уравнения
и неравенства,
содержащие модуль.

2.

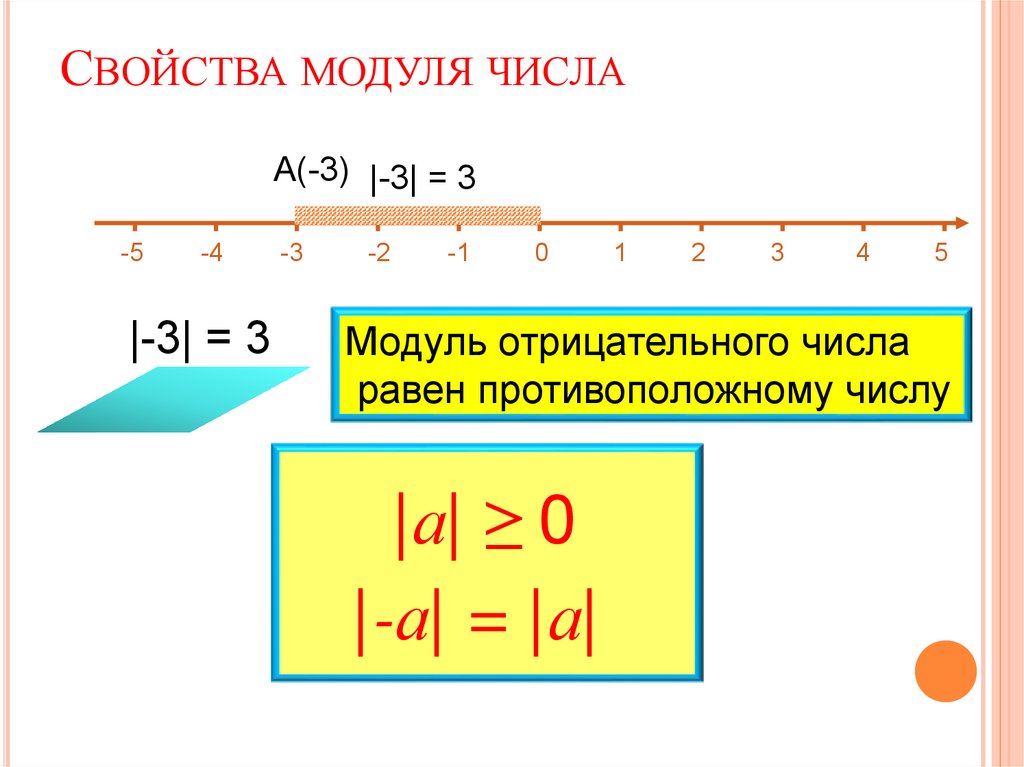
СВОЙСТВА МОДУЛЯ ЧИСЛА
|3| = 3
-5
-4
|3| = 3
-3
-2
-1
0
1
А(3)
2
3
4
Модуль положительного
числа равен самому числу
|0| = 0
Модуль нуля равен нулю
5

3.

СВОЙСТВА МОДУЛЯ ЧИСЛА
А(-3) |-3| = 3
-5
-4
|-3| = 3
-3
-2
-1
0
1
2
3
4
5
Модуль отрицательного числа
равен противоположному числу
|а| ≥ 0
|-а| = |а|

4.

МОДУЛЬ ЧИСЛА
х 5
а, если а 0,
а
а, если а 0
х 0, то х 5
х 0, то х 5

5.

МОДУЛЬ ЧИСЛА
а, если а 0,
а
а, если а 0
х 2 5 х 2 0, то х 2 5
х 7
х 2 0, то х 2 5
х 3

6.

Запомни!
Если а=0,
то уравнение
|х|=а имеет один корень.
Например:
|х|= 0
х=0

7.

Запомни!
Если а<0,
то уравнение
|х|=а не имеет корней.
Например:
|х|= – 7
не имеет корней

8.

а, если a 0,
а
a, если а 0.
Модуль числа
х 3
х 3,
х 3.
IIIIIIIIIIIIIIIIIIIIII
I I I I I I I I I I I -3
I I I I I I I I I I I3
х
х [ 3; 3]
3 х 3

9.

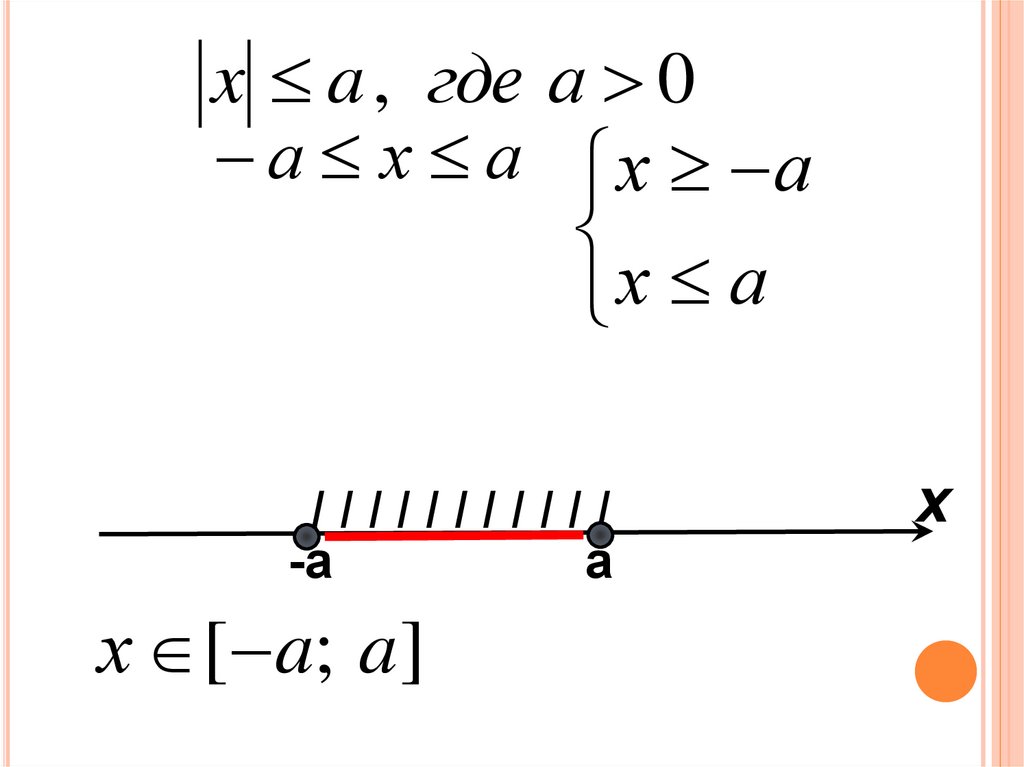
x a , где а 0
а х а х а
х а
IIIIIIIIIII
-а
а
х [ a; a]
х

10.

Модуль числа
х 3
I I I I I I I I I -3
I
а, если a 0,
а
a, если а 0.
x 3,
x 3.
IIIIIIIIIII
х
3
х ( ; 3), 3;
х 3, x 3.

11.

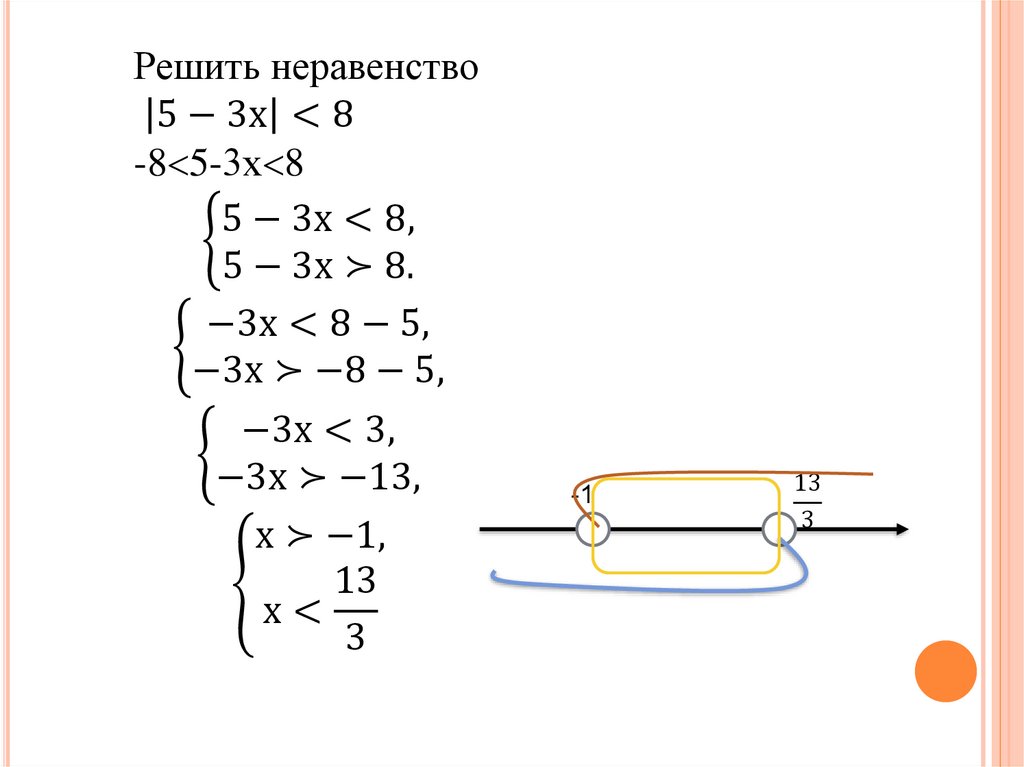
Решить неравенство
5 − 3х < 8
-8 5-3х 8
5 − 3х < 8,
ቊ
5 − 3х ≻ 8.
−3х < 8 − 5,
ቊ
−3х ≻ −8 − 5,
−3х < 3,
ቊ
−3х ≻ −13,
х ≻ −1,
13
ቐ
х<
3
-1
13
3

12.

Решить неравенство |5 – 4х|< 1
5 4 х 1
5 4 x 1
5 – 4x > – 1
– 4x> – 6
x < 1,5
5 – 4x < 1
– 4x< – 4
x>1
1
Ответ: (1; 1,5)
1,5
х

13.

Запомни!
Если а<0,
то неравенство
|х|≤а не имеет решений.
Например:
|х|≤ – 7
не имеет решений

14.

Запомни!
Если а≤0,
то решениями неравенства
|х|≥а являются все числа
Например:
|х|≥ – 7
х – любое число

15.

Запомни!
Если а=0,
то неравенство:
|х|≤а имеет единственное
решение.
Например:
|х|≤ 0
х=0

16.

x a,
x a.
х а, где а 0
I I I I I I I I I -а
I
IIIIIIIIIII
а
х
х ( ; a), a;
х a, x a.

17.

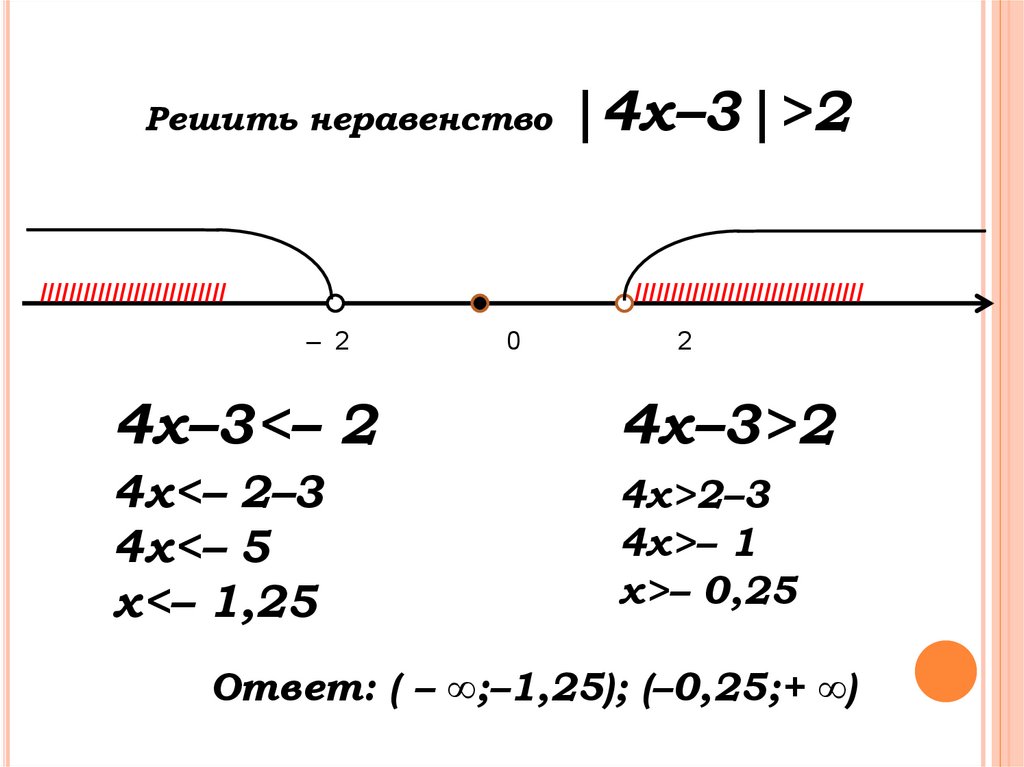
Решить неравенство
//////////////////////////
|4х–3|>2
////////////////////////////////
– 2
0
2
4x–3<– 2
4x–3>2
4x<– 2–3
4x<– 5
x<– 1,25
4x>2–3
4x>– 1
x>– 0,25
Ответ: ( – ∞;–1,25); (–0,25;+ ∞)

18.

ЗАДАНИЕ:
№156 (1,3);
№157 (1,3,5);
№158 (1,3).

19.

ДОМАШНЕЕ ЗАДАНИЕ: СТР. 62 ЧИТАТЬ
№158(2,4,6); №155 (2); №156 (2); №157
(2,4,6).